变截面压弯椭球柱面反射镜优化设计
2022-05-28祝万钱任祖洋金利民
李 桐,王 楠,祝万钱,任祖洋,金利民,薛 松*
(1.中国科学院上海应用物理研究所,上海 201800;2.中国科学院大学,北京 100049;3.中国科学院上海高等研究院,上海 201800)
1 引言
在同步辐射光束线中,通常采用各种类型的光学组件对同步辐射光进行偏转、准直、分光和聚焦等,最后传输到实验站中[1]。聚焦镜作为其中一个关键设备,具有光束准直、聚焦、偏转、抑制高次谐波等功能。同步辐射光束多为掠入射反射模式,为获得足够的接收角,需要反射镜在光线入射方向(即子午方向)具有一定的尺寸,所以反射镜通常为横向略窄而轴向较长的长条形[2]。但是镜子一旦加工成型后,其面形很难改变,只能满足特定参数要求的线站需求,灵活性不够[3]。因此需要通过压弯机构进行反射镜压弯,根据不同的使用需求,控制压弯力或者杆件位移来压弯不同的面形,从而得到各种面形的反射镜。不同光束线上压弯镜的形状、作用和尺寸都不一样,因此压弯机构也会有较大的差别。
20 世纪 70 年代,基于传统望远镜等光学元件加工方式,以德国蔡司、法国 Winlight、Thales SESO、日本大阪大学及 JETC 公司等为代表的公司逐步开始了同步辐射元件的研制[4]。随着同步辐射光源的发展,光源的发射度越来越小,对聚焦镜的光学要求也越来越严格。我国在压弯机构的研究起步较晚,但目前国内科研与工程人员在努力追赶最先进的国际水平(压弯精度≤0.2 μrad)。上海光源一期建设时,我国自主研发的压弯机构的压弯精度可以达到1.5~2.0 μrad 左右[3],经过多年努力,压弯机构的压弯精度可以达到0.5 μrad,甚至更好的水平。在制造精度有限的条件下,椭圆聚焦被认为是同步辐射光束线中理想的聚焦模式[1],光源点和成像点分别位于椭圆的两个焦点上,因此理论上压出近乎完美的椭圆可以减少光束线的传输误差[5]。
反射镜压弯是基于梁的弯曲变形理论,通过理论计算,反射镜的变宽高次曲线可以使椭圆压弯的理论残差趋近于零,但是受反射镜加工难度和成本限制,实际上多采用梯形变宽或多段梯形变宽反射镜。梯形变宽反射镜椭圆压弯必然有无法消除的理论误差,本文针对特定理想椭圆曲线且存在弧矢半径槽导致反射镜惯性矩变化系数与梯形变宽系数不相等的情况下进行梯形反射镜尺寸设计和模拟验证,设计要求压弯理论残差小于0.1 μrad。
2 反射镜参数计算及优化设计
2.1 反射镜面形参数
反射镜的面形一般由物距p、像距q和掠入射角 θ确定,本次设计的反射镜面形为椭圆面形[6],椭圆压弯聚焦模式如图1 所示。
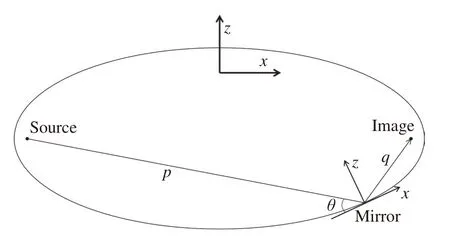
图1 椭圆压弯聚焦原理图Fig.1 Schematic diagram of elliptical bending focus
根据椭圆标准方程,结合反射镜面形参数,可以严格推导出理想压弯椭圆面形方程[7-8]:
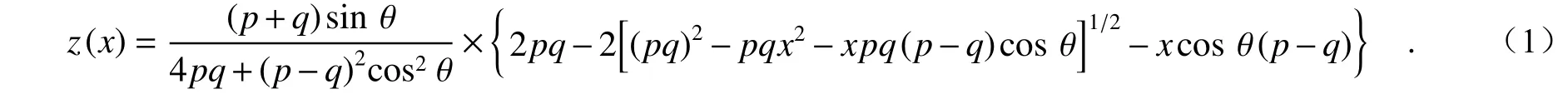
在实际的工程计算中,为了便于进行理论计算,通常采用椭圆方程在反射镜中心处的麦克劳林级数展开式,一般选在二次方之前。而对于最终的面形斜率误差求解则采用公式(1)中的理想椭圆方程,其麦克劳林级数表达式[7,9-10]为
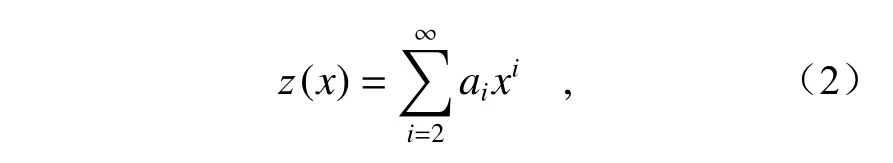
其中的参数ai为
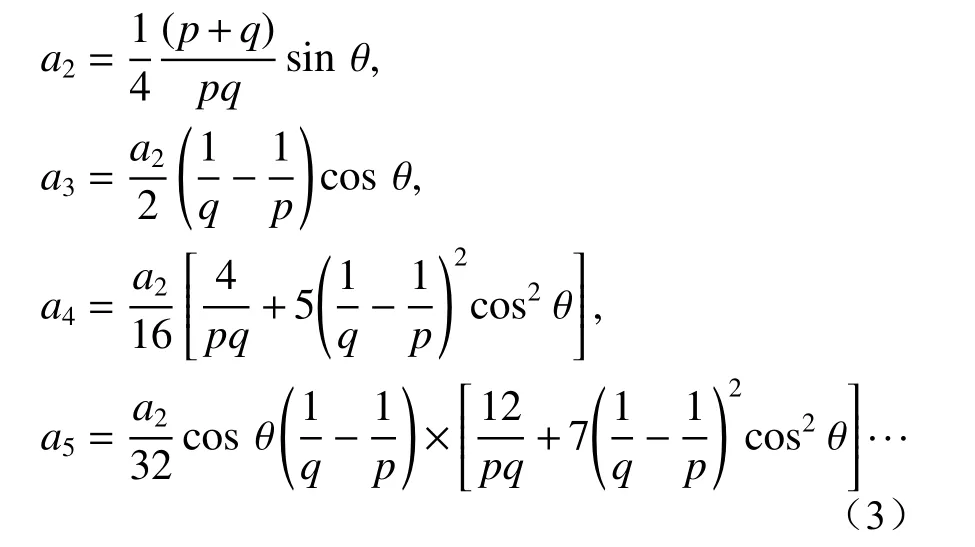
在同步辐射光学中,光学元件的面形精度通常采用光学表面的斜率误差进行评价,在本文中定义为压弯变形曲线与理想椭圆曲线斜率方程差值的均方根。
2.2 梁的弯曲
在同步辐射中,由于反射镜的长宽比很大,因此反射镜的压弯可以简化成梁的压弯,如图2所示。
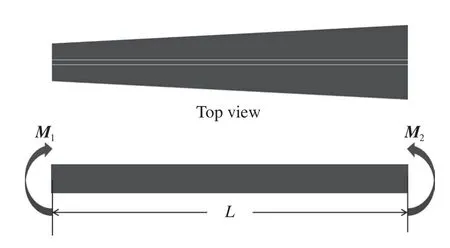
图2 压弯镜示意图Fig.2 Schematic diagram of the bending mirror
在材料力学中,梁弯曲的一般方程可以表示为
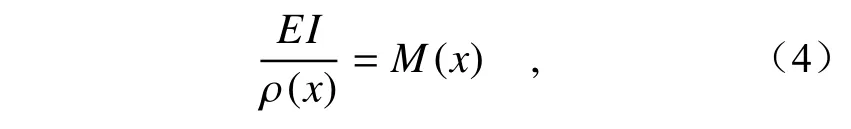
其中,ρ(x)为反射镜曲率半径,E为反射镜基板材料的杨氏模量,M(x)为弯矩方程,I为柱面镜截面的惯性矩(I(x)=b(x)t3/12,b和t分别为反射镜的宽度及厚度)。根据材料力学公式可知,M(x)=,其中L为反射镜长度。
本次设计反射镜的主要参数如表1 所示。
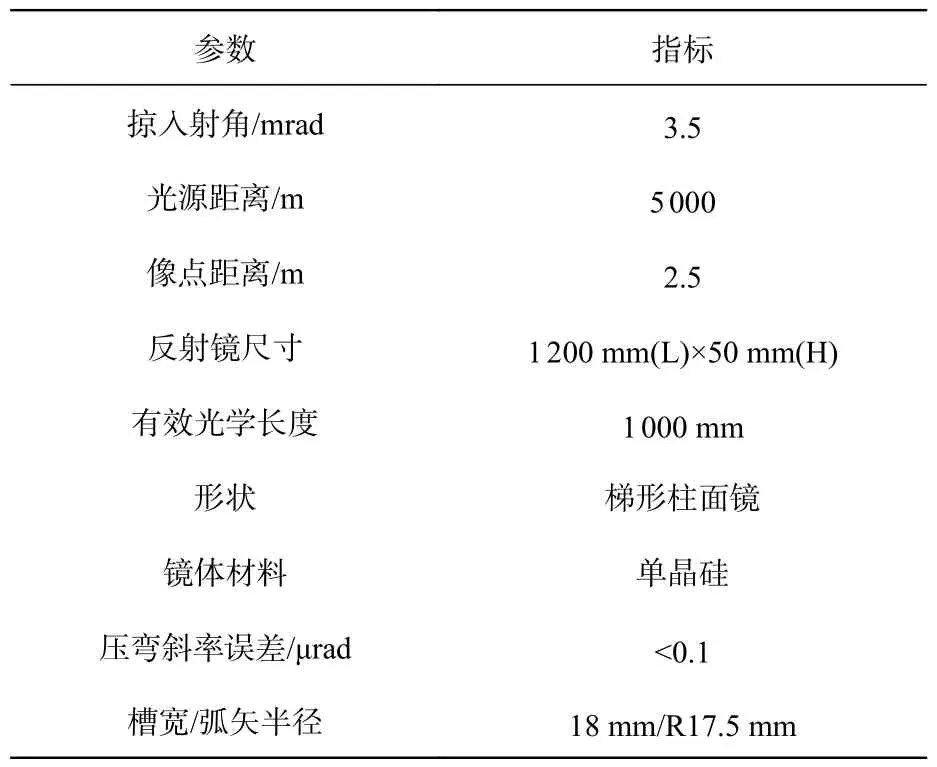
表1 反射镜设计参数Tab.1 Main indicators of the designed mirror
基于变宽度压弯椭圆柱面微聚焦镜理论中的公式可得出[9],反射镜两端的宽度分别为49 mm 和90 mm,反射镜两端弯矩分别为M1=81.138 2 N·m,M2=91.468 6 N·m。将上述结果带入所建立的反射镜模型后进行仿真分析,建立的三维模型如图3 所示。

图3 反射镜模型轴测图Fig.3 Axonometric view of mirror model
使用有限元方法对反射镜压弯进行力学分析,将反射镜模型进行网格划分,采用六面体单元,网格尺寸为2 mm,网格划分如图4 所示。
图4 模型网格划分Fig.4 Meshing results of the mirror model
本次仿真分析中反射镜的材料属性如表2所示。

表2 用于仿真分析的材料属性Tab.2 Properties of the material used in the simulation analysis
将弯矩施加在反射镜两端,对反射镜两端进行简支梁约束,仿真得出反射镜面形,其面形如图5 所示。
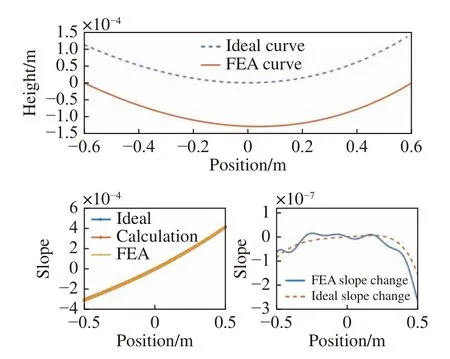
图5 反射镜压弯面形及斜率分析Fig.5 Analysis of the bending surface shape and slope of the mirror
仿真计算出的斜率误差与原计算公式得出的系统斜率误差对比如表3 所示。由于本次设计的反射镜包含弧矢半径柱面,仿真斜率误差与系统斜率误差相差很大,因此,无法忽略弧矢聚焦槽口对斜率误差的影响,而原公式只对平面反射镜适用,这就需要重新对公式进行推导计算。
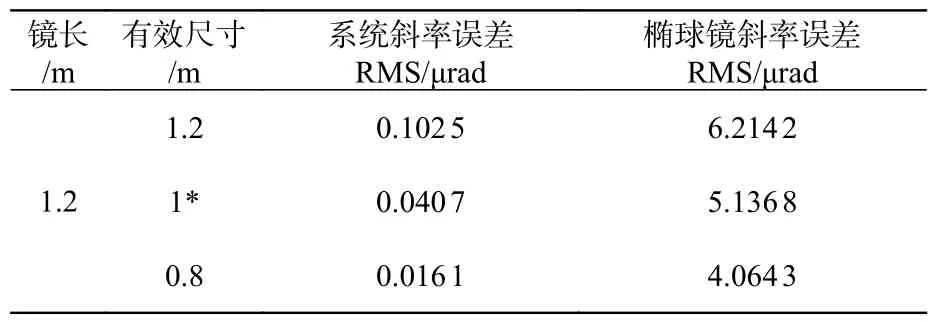
表3 本文计算的与初始公式计算的斜率误差对比Tab.3 Comparison of the slope errors calculated in this paper with that calculated by the initial formula
2.3 反射镜优化设计
在材料力学中,可以将变截面惯性矩看作多个简单截面惯性矩进行计算。本文研究的反射镜的截面可以简化成变矩形截面与槽截面的差值,由于槽口截面一定,矩形截面宽度随反射镜长度的变化而变化,导致反射镜截面的形心也在不断变化,此前惯性矩公式无法准确表述各截面的实际惯性矩。反射镜截面惯性矩计算示意图如图6 所示。
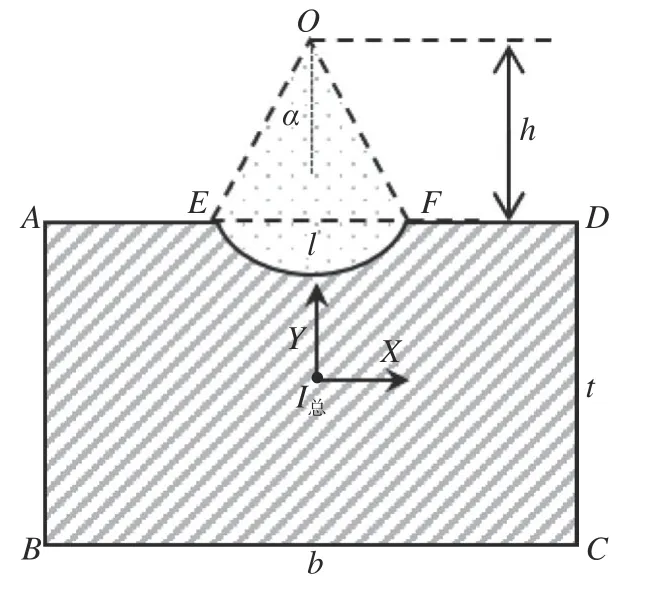
图6 截面惯性矩示意图Fig.6 Schematic diagram of the section moment of inertia
根据移轴定理公式计算截面惯性矩,其形心(yc)坐标公式:
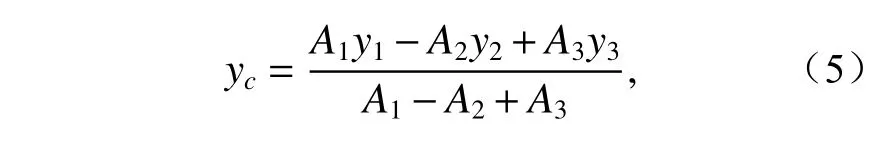
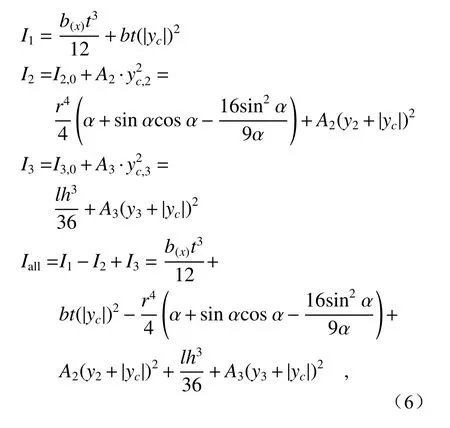
其中I1,I2,I3分别为矩形ABCD、扇形OEF、三角形OEF的惯性矩,Iall为截面惯性矩,yi为各部分形心到矩形ABCD中心X轴的距离。
从式(5)、式(6)可以看出,截面惯性矩中的变量为反射镜的宽度b,大小与反射镜长度成正比,其余惯性矩皆为常数。通过对该尺寸参数下的截面进行惯性矩计算,得到在反射镜中间处截面惯性矩为:I0=711 521.571 mm4。由于惯性矩与反射镜长度成正比,因此可以将惯性矩进行线性表述,计算得其斜率值k′≈−0.5。通过程序对公式进行验算,计算得出的反射镜各点处的惯性矩如图7 所示。
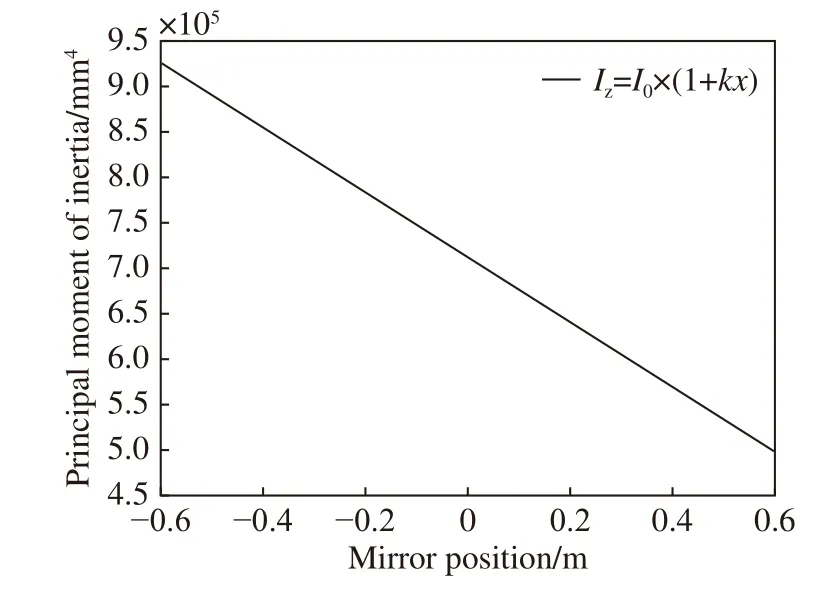
图7 反射镜各点处惯性矩Fig.7 Moment of inertia at each point of the mirror
其弯曲方程[7,9-11]可以转换为
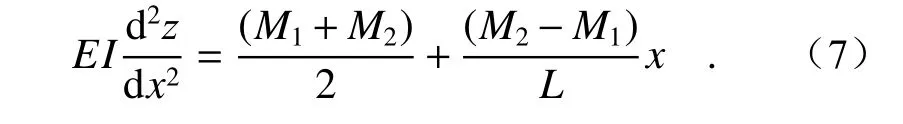
对反射镜两端宽度进行求解,公式推导如下所示

在公式(8)中,反射镜宽度b为关于反射镜长度的一次函数,因此惯性矩公式可以简化为
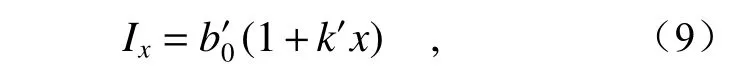
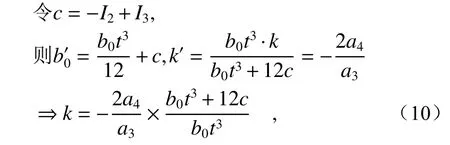
其中b0为反射镜中心处宽度,k′为惯性矩与反射镜长度关系的斜率系数。最终计算得出的反射镜宽度中的斜率k=−0.488 3。代入=b0(1+kx)中即可求得反射镜两端宽度分别为49.5 mm 和90.5 mm。
在实际工程应用中反射镜椭圆聚焦时其面形方程可以通过麦克劳林展开式来进行简化计算,其一般方程为
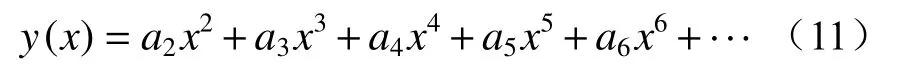
对其麦克劳林展开方程进行二次求导,并代入公式(6)中可以得出反射镜椭圆压弯时两端所需弯矩大小,其公式[10]为
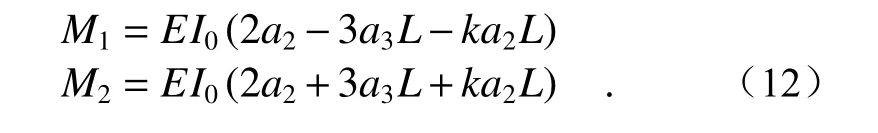
反射镜压弯斜率误差RMS 可以通过对反射镜的曲率方程进行积分化简计算得出,将其曲率方程化简为以下方程[8]再进行积分
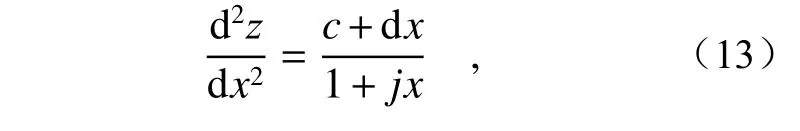
其中参数c,d,j分别为
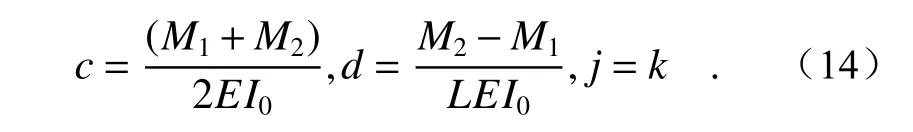
由式(13)、式(14)可以计算得出在实际工程中椭圆压弯反射镜的斜率表达式
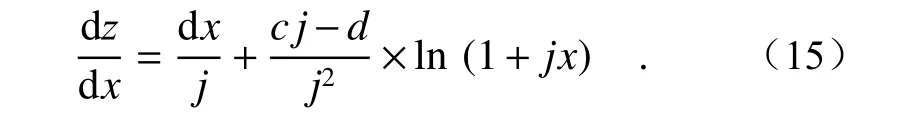
至此,修正后的反射镜两端宽度分别为49.5 mm 和90.5 mm,两端力矩M1,M2分别为79.177 4 N·m,89.252 5 N·m。将修正后的力矩值代入仿真计算中,修正前后斜率误差RMS 值对比如表4 所示。
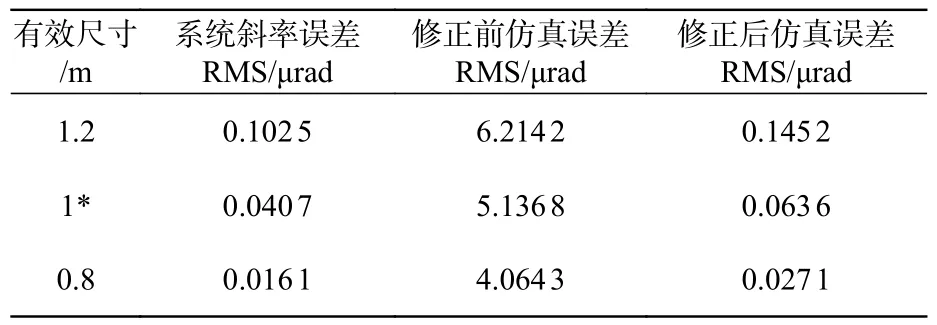
表4 修正前后斜率误差对比Tab.4 Comparison of the slope errors before and after correciton
对比发现,修正后斜率误差RMS 值得到了数量级上的提升,同时,修正后的斜率误差RMS 值更接近系统误差值,可以认为计算值可靠。本次反射镜需求有效光学尺寸为1 m,可以看出将惯性矩为线性分布代入公式计算出的仿真误差更贴近系统误差值。本次修正后的公式基本适用于各类变截面反射镜的优化设计,最终的修正效果显著。
3 结论
本文基于椭圆柱面镜聚焦原理,对反射镜整体参数进行设计及优化,并根据实际需求,推导了完整的计算、优化流程。在光学参数及反射镜长度一定时,通过公式计算设计出反射镜的两端宽度,同时优化计算出压弯弯矩大小,采用有限元分析校核了该优化的有效性。在反射镜有效长度为1 m 的情况下,斜率误差RMS 值为0.063 6 μrad,与系统斜率误差RMS 值0.040 7 μrad 更贴近,同时满足压弯机构引入误差<0.1 μrad 的设计需求。该方法不仅针对此类截面有效,针对不同截面的反射镜依然可以参照此计算思路进行优化设计。
