利用SAS软件中的PROC GLIMMIX过程步实现二分类数据的网络meta分析*
2022-05-28陈掌珠黄碧芬郑建清
陈掌珠 黄碧芬 郑建清△
【提 要】 目的 介绍利用SAS软件中的PROC GLIMMIX过程步实现二分类数据的网络Meta分析。方法 以《高级Meta分析方法——基于Stata实现》一书第十七章第三节的戒烟率数据作为实例,利用SAS软件PROC GLIMMIX过程步实现基于广义线性混合效应模型的Meta分析,并提供编程代码。结果 PROC GLIMMIX过程步可以分别拟合固定效应模型NMA和随机效应模型NMA。实例数据的固定效应NMA分析显示,干预措施2、3、4与干预措施1相比的OR点估计值和95%CI分别为1.2531(0.9804,1.6026)、2.1231(1.8939,2.381)、2.2936(1.6287,3.2258);而随机效应分别为1.5898(0.7918,3.1949)、2.2026(1.4641,3.3113)、2.8011(1.3106,5.988)。结论 PROC GLIMMIX可以非常方便地拟合二分类数据的网络Meta分析,并通过均数差分图显示成对比较,具有直观的统计显示效果。
在临床医学领域,传统的Meta分析方法涉及的是干预和对照之间的比较,通常对照为安慰剂或其他常规疗法,而干预则特指某种新疗法,这种Meta分析被称之为成对Meta分析(pairwise meta-analysis)或经典Meta分析[1]。在存在足够数量的针对特定临床问题的原始研究的情况下,针对双臂研究的传统Meta分析可以获得两种不同治疗方法的效果比较结果,提高检验效能,比较容易获得具有统计学显著性的结果[2]。但在临床实践中,某些疾病存在多种新型治疗方法,临床医生、患者或政府部门的决策者需要横向比较这些治疗方法的差别。在这种情况下,尤其缺乏头对头比较的原始研究时,传统Meta分析方法变得无能为力[2]。为了克服传统Meta分析的缺陷,在过去的十年里,针对随机对照试验的网络Meta分析(network meta-analysis,NMA)作为传统meta分析的延伸而被引入循证医学,其优点是在缺乏直接头对头比较的情况下,实现多种干预措施的间接比较[3]。网络Meta分析的核心思维是多重治疗比较(multiple treatment comparison,MTC),这种新方法对临床研究人员很有吸引力,因为这种Meta分析方法可以确定最佳可行的干预措施。然而,尽管成对Meta分析的假设条件可以被系统评价员很好地理解,但是与NMA相关的假设则更复杂,而且容易被误解。与成对Meta分析相比,网络Meta分析可以获得更多的可视化证据,从而有效评价不同干预措施之间的相对有效性,并对干预措施进行排序。然而,在现实实践中,NMA的实施仍然存在多种挑战,尤其对于模型的构建更是NMA最困难的任务。在本文中,笔者介绍了一种基于广义线性混合模型(generalized linear mixed models,GLMMs)的NMA模型,该模型已被Jones和Madden等学者证明是一种非常高效的NMA方法[4-5],但目前国内尚无学者介绍该模型的具体实践。在SAS软件中,拟合广义线性混合模型的过程步是PROC GLIMMIX,因此本文的编程基础是PROC GLIMMIX。
基于广义线性混合模型的网络Meta分析模型简介
1.广义线性混合模型理论及介绍
GLMMs是广义线性模型(generalized linear models,GLMs)和线性混合模型(linear mixed model,LMM)的扩展形式,于二十世纪九十年代被提出,是一种比较新型的统计模型。GLMMs借鉴了混合模型的思想,因此可以通过随机效应来解释数据间的相关性,也可以解决数据存在的过度离散(overdispersion)、异质性(heterogeneity)等问题。此外,GLMMs模型中,因变量不再要求满足正态分布。
GLMMs是在线性混合效应模型的基础上进行扩展的,LMM的基本表达形式是[6]:
y=βX+γZ+ε
(1)
对于GLMMs,令线性预测因子(linear predictor)η表示固定效应和随机效应的组合(也就是说随机误差不包含在内),即:
η=βX+γZ
(2)
令g(·)表示链接函数(link function),用于描述影响因子线性组合的值与因变量之间的关系,h(·)为g(·)的反函数,则有:
g(E(y))=η,E(y)=h(η)=μ,因此,y=h(η)+ε。
因此,GLMMs模型表述为:
μy=E(yi|ui,Xi)=ηi=X′iβ+Z′iγi
(3)
ui为随机效应项,是反应变量yi的条件分布的期望;条件均数ui(考虑了随机效应)通过连接函数g(·)与条件线性预测值ηi连接。
g(μi)=ηi=X′iβ+Z′iγi
(4)
式(4)为广义线性混合模型的一般式,yi是n×1维的反应变量,在随机效应ui的条件下独立,服从指数分布族,可以是二项分布、Poisson分布、Gamma分布等[7-8]。
在公式(3)中,Xi为解释变量,β为固定效应参数向量,ui是随机效应,服从均数为0,方差协方差矩阵为γ的多变量正态分布,ui解释了由不可测因子引起的类间异质性和同一类内观测到的相关,不同类间的ui是相互独立的,Zi是与随机效应相关的解释变量[9]。设计矩阵分固定效应X与随机效应Z两部分。分析的数据不同可以选择不同的联结函数g(·),可以拟合含随机效应的logisitc回归等多种模型。
2.基于广义线性混合模型的网络Meta分析(GLMM-NMA)理论及介绍
与成对Meta分析一样,网络Meta分析同样可以分为固定效应模型分析和随机效应分析,但在实践操作中,现有的统计软件,如R、GeMTC和Stata等软件则几乎不提供固定效应模型的计算方法[10]。本文则介绍了基于GLMMs的固定效应模型和随机效应模型。需要注意的是,本文讨论的Meta分析模型是以对数比值比(log-odds ratio)为效应尺度的,其他服从正态分布的效应尺度也适合本文提供的模型。
(1)基于固定效应模型的GLMM-NMA
在固定效应NMA模型中,效应值log-odds被假设具有线性效应,固定效应的组成部分包括研究效应和治疗效应。该模型是以对数-线性链接函数为尺度的二分类数据的广义线性模型的实际应用。
假设第i(i=1,…,N)个研究中受试者在第j(j=1,…,K)个治疗组中的事件发生概率为pij,对pij进行logit转换,则有:
(5)
其中,i=1,…,N,j=1,…,K。
假设受试者是独立的,第i研究的治疗组j的样本量为nij,发生的事件数为rij。假设rij服从二项式分布(binomial),即rij~Bin(nij,pij)。需要注意的是,上述模型并没有截距项。此外,这个模型的构建并不是唯一的,研究人员可以向si添加另外组分,然后从tj中去除该组分,得到的模型完全相同。该模型的构建有一个约束条件:默认情况下,SAS将添加一个截距用于描述全局均值,而且约定si和tj最后一个亚变量作为对照,即sN=0和tK=0,但这里的模型省略了截距项,并将第一个哑变量设置为对照(即t1=0)[5]。
在SAS中,PROC GENMOD、PROC LOGISTIC和PROC GLIMMIX等三种程序步可以非常方便地拟合该模型[4]。
(2)基于随机效应模型的GLMM-NMA
随机效应模型的结构与固定效应模型相似,多出来的部分是假设不同研究中的治疗效应因研究而异。在固定效应模型的基础上,线性预测变量增加了随机效应项:
(6)
其中N个研究νij值构成的向量νi,具有独立性质的K维多变量正态分布N(0,Ω);同样要求t1=0。
该模型中,si仍然属于固定效应部分。将si锁定为固定效应部分,可以有效避免不同研究间的潜在偏倚问题。在这种限制条件下,可以确保不同试验的治疗差异均来源于随机化信息。基于PROC GLIMMIX的编程方式有很多种,附录代码4是GLIMMIX过程步拟合随机效应模型的默认代码。此模型假设矩阵Ω=σ2IK。也就是说,不同试验中治疗随机效应是独立的,且具有相等的方差σ2。一般不建议使用此模型,因为该模型会严重低估方差σ2。
Lu和Ades证明了该模型的缺陷,因此,Lu和Ades建议随机效应模型应该直接关注不同试验的治疗差异及其在不同研究间的变异[11]。Lu和Ades将pij定义为:
(7)
对于所有第i=1,…,N个研究,δi1的参数被限定为零,同时假设(δi1,…,δiK)~N((d2,…,dK),∑)。
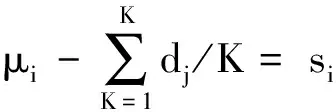
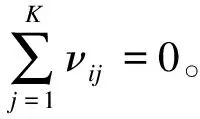
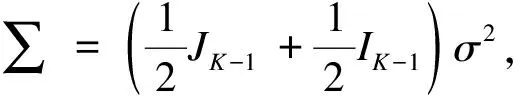
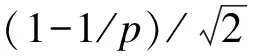
资料与方法
1.实例数据介绍
为了比较上述三种模型[公式(5)、公式(6)、公式(7)]的差别,本文结合实例数据进行模型拟合。该实例数据来源于“AHCPR Smoking Cessation Guideline Panel”报告,是目前介绍NMA最广泛引用的实例数据[11-13],在《高级Meta分析方法——基于Stata实现》一书中也被引用[14]。由于Stata是目前最广泛使用的NMA软件,本文以文献[14]中的Meta分析结果作为对照,比较本文模型的有效性。
本文采用的实例数据集的详细信息如表1所示,该数据集文献[14]中的横向数据集经过本文附录代码1转换后的纵向数据,受篇幅所限,表1只纳入前10个研究数据。

表1 待分析数据集
表1的数据存储在名为NMA_data2的数据集中。相关的变量解释如下:Design代表研究设计方法;Study代表研究编号;Narm代表某试验的臂数,也就是几个干预组;Index用于指引某研究内的干预组编号,根据治疗变量t排序后分别标示,最大值为Narm;Revindex是Index的反向标示;Notfirst用于指引Index标示下的非第一组臂,如果为第一组,则Notfirst取值为0,否则为1;NotLast意义与Notfirst相同,但指引最后一组。r代表某干预组内成功戒烟患者数;n代表该干预组的样本量;trt代表干预组(本例trt取值为1、2、3、4,代表4种干预措施,分别是no contact、self-help、individual counselling、group counselling,即无接触戒烟、自助戒烟、个体辅导、团体辅导等)。
2.SAS代码简介
本文提供了SAS软件中实现了适合NMA的不同格式数据集的转换代码,鄢金柱等人提供了另一种转换代码,但本文代码更简洁[15]。附录代码同时提供了基于PROC GLIMMIX过程步拟合广义线性混合效应模型的代码,为了便于读者学习,我们同时给出了固定效应模型和随机效应模型的拟合代码。同时在PROC GLIMMIX中添加图片输出参数,读者只需设置“图片保存目录”,即可便捷地输出各种期刊格式的图片到指定的文件夹。
结 果
1.基于标准策略的NMA分析结果
表2是文献[14]第362页的Meta分析结果,该结果来源于Salanti等人提出的基于标准对比模型(standard contrast-based model),也是Stata软件实现NMA的核心模型,也被称为标准策略模型。此处提供相关Meta分析结果是为了方便比较本文构建模型的有效性。

表2 基于Stata标准对比模型的NMA分析结果
2.基于GLMMs固定效应模型的NMA分析结果
表3是PROC GLIMMIX拟合计算的单臂效应值log-odds,通常不具有实际意义,但通过两两对比,获得表4的效应差值,则是系统评价员最关心的效应值。如干预1和干预2对比,干预1的log-odds效应值-干预2的log-odds效应值即可得到效应差值,该效应差值为log-OR,通过逆函数exp即可获得OR值。

表3 基于GLMMs固定效应模型的单臂效应值Meta分析结果
从表4可以看出,两两对比中,只有1-3,1-4,3-2,4-2之间的对比具有统计学差异,说明这些干预效应的差值具有统计学意义。图1是模型提供的差分图,以对角线为统计学检验的界值,效应线跨越对角线则提示差异无统计学意义。

表4 基于GLMMs固定效应模型的NMA分析的两两对比结果

图1 基于GLMMs固定效应模型的NMA分析差分图
3.基于GLMMs随机效应模型(1)的NMA分析结果
表5、表6是随机效应模型的拟合结果。模型的参数解释与固定效应模型相同,但根据表6可以看出,3-2,4-2之间的对比不具有统计学差异,与固定效应模型具有差别。

表5 基于GLMMs随机效应模型(1)的单臂效应值Meta分析结果

表6 基于GLMMs随机效应模型(1)的NMA分析的两两对比结果

图2 基于GLMMs随机效应模型(1)的NMA分析差分图
4.基于GLMMs随机效应模型(2)的NMA分析结果
表7、表8是第二种随机效应模型的拟合结果。
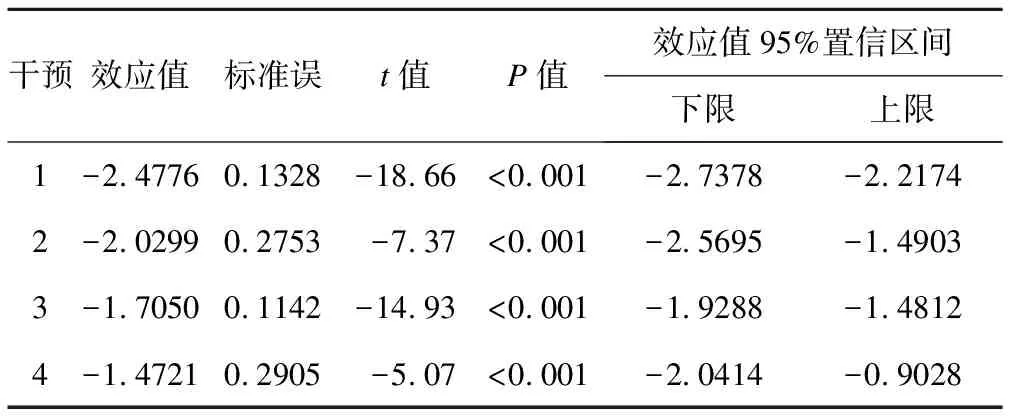
表7 基于GLMMs随机效应模型(2)的单臂效应值Meta分析结果
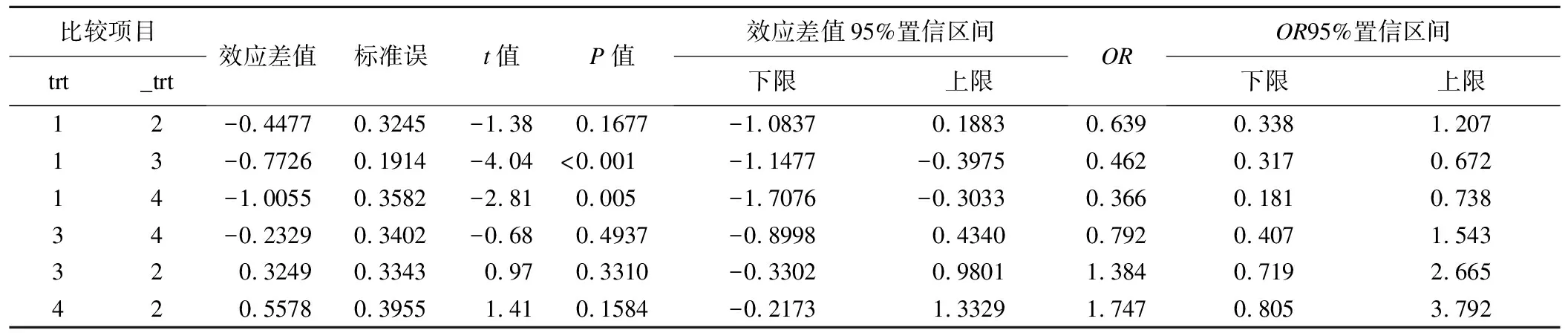
表8 基于GLMMs随机效应模型(2)的NMA分析的两两对比结果
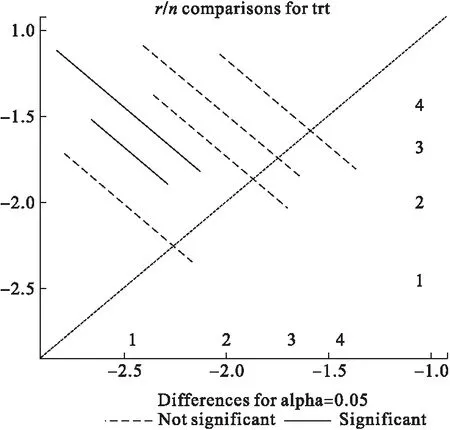
图3 基于GLMMs随机效应模型(2)的NMA分析差分图
5.两种GLMMs随机效应模型的NMA分析结果比较
表9是本文两种随机效应模型的协方差参数估计值,模型(1)的协方差参数明显低于模型(2)。

表9 基于GLMMs随机效应模型协方差参数估计
讨 论
在临床实践中,许多新的治疗措施缺乏“头对头研究(head to head)”的证据,即直接比较证据。在这种情况下,传统两两比较的Meta分析方法无法给出比较结果,临床医生无法获得孰优孰劣的准确判断[16]。网络Meta分析是一种将多项研究(通常是随机试验)的证据结合在一起,进行多重比较,从而确定最佳干预措施的Meta分析方法。它的主要特点是能够同时通过直接比较和间接比较获得两种治疗措施的比较证据。在缺乏头对头研究的情况下,NMA是获得间接证据的最优方法。
在所有统计软件中,Stata是最常用的NMA软件之一,其核心模块是mvmeta程序包,可以执行多变量Meta分析和Meta回归[17]。利用mvmeta程序包可以实现网络Meta分析模型的频率估计[18],但mvmeta包需要复杂的编程代码。相比之下,基于mvmeta包的Network程序包则更为友好,可以通过简洁的代码实现NMA[13]。鉴于Network程序包的易用性,本文采用Stata的Network程序包的计算结果作为对照。从核心统计模型来看,无论是Stata软件mvmeta程序包还是Network程序包,都是运用多元线性回归统计理论来实现多治疗方法比较的NMA[19]。这种简单的操作模式,可以解决NMA数据的内在复杂性,已被证明是一种非常有效的多元分析方法。
与多元线性回归统计理论不同,本文构建的NMA方法是基于广义线性混合模型来实现的。这种模型最大的优势是无需对因变量进行正态分布假设,同时可以通过不同的链接函数将观测的均数向量与模型参数联系起来,极大地扩大了模型的应用范围。GLMMs的另一个优点是引入了随机效应项,并且这种随机效应项是以非线性形式的方式进入模型。在GLMMs模型中,引入的各项随机效应变量既可以相互独立,又可以相关。对于GLMMS模型而言,相关的结局变量可以是连续性变量,也可以是分类变量(包括二分类变量、有序多分类、无序多分类等)。因此,GLMMs不仅可以处理独立数据,也可以处理相关数据,甚至对纵向数据、过离散数据也能够进行统计建模[20]。因此,广义线性混合模型被誉为是最强大的统计模型之一,并被越来越多的学者引入Meta分析领域[9,21],并被引入NMA[22]。我们前期的研究表明,GLMMs同样适用于多结局测量的多变量Meta分析[23],在经典二分类数据的Meta分析中也是一种有效的统计模型[24-25]。
在SAS软件中,实现广义线性混合模型对应的过程步是PROC GLIMMIX,但本文的统计模型同样可以采用PROC GENMOD实现,但仅限于固定效应模型[22]。对于多干预试验的Meta分析,GLMMs采用简单的数据建模,即可实现这类复杂数据的NMA。从本文的分析结果来看,GLMMs的结果与Stata的结果相当接近[14]。与Stata的组间结果相比,PROC GLIMMIX则通过回归系数的方式,给出了单臂的对数比值(log odds)作为组水平的效应值,系统评价员可以通过不同干预的单臂效应值的减法计算来评价不同干预的效应差别,这对系统评价员来说极为方便。
与Stata软件中的Network模块给出的森林图不同,PROC GLIMMIX给出的是均数差分图,并通过线型和线色的差异来显示具有统计学意义的成对Meta分析结果。以本文图1为例,差分图输出的结果表明,干预1与干预4的LS均值差异在5%的水平上具有统计学意义,其LS均值差为(-0.8298±0.1747),相应的OR为0.436,95%CI为(0.31,0.614),提示与干预4相比,干预1更能提高戒烟效果。
SAS软件需要一定的编程基础,这是该软件的不足,但以PROC GLIMMIX实现基于广义线性混合效应模型的Meta分析,则为NMA的实施提供了新的思路与途径[26]。PROC GLIMMIX可以通过“random”语句来设置随机效应模型,通过简单的编程,可以同时给出固定效应模型Meta分析结果和随机效应模型Meta分析结果。据笔者所知,目前常用的主流NMA软件,如R、GeMTC软件、OpenBUGS等,只有PROC GLIMMIX过程步是基于GLMMs实现二分类数据的NMA。PROC GLIMMIX无法输出森林图和网状关系图,这是本文模型的不足之处,但森林图的绘制,可以借助SAS的其他制图程序来实现。
综上所述,PROC GLIMMIX可以非常方便地拟合二分类数据的网络Meta分析,并通过均数差分图显示成对比较,具有非常直观的统计显示效果。
附录代码1:
title “数据集建立及资料录入”;
Data NMA_data1;
length design $20.;
input study design ar an br bn cr cn dr dn@@;
datalines;
1 ACD 9 140 ..23 140 10 138
……
;
run;
附录代码2:
title “横向数据转换成纵向数据”;
data NMA_data2;
set NMA_data1 end=myend;
drop ar an br bn cr cn dr dn;
Narm=((ar+an) > 0) +((br+bn) > 0) +((cr+cn) > 0)+((dr+dn) > 0);
Index= 0;
if ar+an >0 then do;
Revindex=Narm-index;index=index+1;
Notfirst=(index>1);NotLast=(index r=ar;n=an;trt=1;output; end; if br+bn >0 then do; Revindex=Narm-index;index=index+1; Notfirst=(index>1);NotLast=(index r=br;n=bn;trt=2;output; end; if cr+cn >0 then do; Revindex=Narm-index;index=index+1; Notfirst=(index>1);NotLast=(index r=cr;n=cn;trt=3;output; end; if dr+dn >0 then do; Revindex=Narm-index;index=index+1; Notfirst=(index>1);NotLast=(index r=dr;n=dn;trt=4;output; end; run; 附录代码3: title “模型1:基于固定效应模型的NMA分析”; proc glimmix data=NMA_data2 order=data plots=Diffogram; ods listing gpath=“图片保存目录” style=default image_dpi=300; ods graphics/reset imagename=“基于固定效应模型的NMA分析” outputfmt=epsi; title “基于固定效应模型的NMA分析”; class study Trt; model R/N = Study Trt /link=logit dist=bin ddfm=none; lsmeans Trt /diff cl oddsratios; run; 附录代码4: title “模型2:基于随机效应模型的NMA分析(1)”; proc glimmix data=NMA_data2 order=data plots=Diffogram; ods listing gpath=“图片保存目录” style=default image_dpi=300; ods graphics/reset imagename=“基于随机效应模型的NMA分析(1)” outputfmt=epsi; title “基于随机效应模型的NMA分析(1)”; class study Trt; model R/N = Study Trt /link=logit dist=bin ddfm=none; random Trt / subject=Study; lsmeans Trt /diff cl oddsratios; run; 附录代码5: title “模型3:基于随机效应模型的NMA分析(2)”; data jr; set NMA_data2; array x[4]x1-x4; do i=1 to 4; if i<= narm then x[i]=sqrt(0.5)*((i=index)-1/narm); else x[i]=0; end; run; proc glimmix data=jr method=QUAD order=data plots=Diffogram; ods listing gpath=“图片保存目录” style=default image_dpi=300; ods graphics/reset imagename=“基于随机效应模型的NMA分析(2)” outputfmt=epsi; title “基于随机效应模型的NMA分析(2)”; class study Trt; model R/N = Trt Study/link=logit dist=bin ddfm=none; random X1 X2 X3 X4/ subject=study type=TOEP(1); lsmeans Trt /diff cl oddsratios; run;
