自等价编码与白盒实现方案的改进
2022-05-28罗一诺董晓丽
罗一诺,童 鹏,陈 杰,,董晓丽
(1.西安电子科技大学 综合业务网理论与关键技术国家重点实验室,陕西 西安 710071;2.西安电子科技大学 网络与信息安全学院,陕西 西安 710071;3.桂林电子科技大学 广西密码学与信息安全重点实验室,广西壮族自治区 桂林 541004)
在传统密码算法中,设计者大多只考虑了密码算法在黑盒攻击环境下的安全性。随着科技的发展和敌手攻击能力的提高,敌手不仅能访问密码算法的输入和输出,还可以获取算法的内部细节并控制终端,使得原有的密码算法暴露在更强的攻击环境下。CHOW等在文献[1]中称此攻击环境为白盒攻击环境,并提出了白盒密码来应对白盒攻击环境。白盒密码是以软件的形式保护密码算法,使得敌手在不安全的终端环境下也无法提取密钥信息。
白盒密码的设计主要分为两种:一种是基于已有分组密码的白盒实现,使用白盒密码技术对已有的分组密码进行改进,使其在白盒攻击环境中具有与原密码算法相同的功能,同时保证算法在白盒攻击环境下的安全性。2003年,CHOW等[1]首次采用查找表、输入输出编码和双射结合的方法,将密钥和编码信息隐藏在查找表中,对AES进行了白盒实现;此后XIAO等[2]及LUO等[3]对AES的白盒实现分别进行了改进。KARROUMI等[4]基于CHOW等人的方案,使用对偶密码技术设计了一种新的白盒AES。2006年,BRINGER等[5]在白盒实现中添加扰乱项设计了一种白盒AES,该实现方式与CHOW等的设计方法不同。2009年,XIAO等[6]将仿射函数与查找表技术结合,设计了SM4的白盒实现,此后也出现了多个白盒SM4的方案[7-8]。2014年,SU等[9]提出了分组密码CLEFIA的白盒实现,此后也有多个白盒CLEFIA的改进方案[10-11]。2016年,MCMILLION等[12]首次提出基于自等价编码的白盒AES,该方案的设计方法是白盒实现的一种新型设计方法。2020年,RANEA等[13]基于代换-置换网络(SPN)密码S盒的自等价,对拆分、重组后的SPN密码的仿射层进行编码,提出了一种通用的针对SPN结构密码的自等价实现方案,同时提出了一种通用攻击。2021年,王滨等[14]提出了基于AES的动态白盒实现方案。针对分组密码的不同白盒实现的设计,先后提出了BGE攻击[15]、MGH攻击[16]、MULDER等[17]的攻击、潘文伦等[18]的差分攻击、侧信道攻击[19-20]等多种攻击方法。另一种白盒密码是设计白盒环境下新的分组密码算法。2014年后,出现了新的白盒安全的分组密码的设计,区别于传统分组密码以及已有分组密码的白盒实现,它是基于某个安全的结构或某个安全目标设计的,如BIRYUKOV等[21]提出的基于ASASA结构的白盒方案,BOGDANOV等[22]提出的SPACE密码,SHI等[23]提出的SDSRS白盒加密方案等,这些方案能保证在白盒攻击环境下的安全性。2020年,SANDRA在其博士论文[24]中总结了白盒密码的关键技术,包括白盒实现的设计、针对白盒实现的安全性攻击以及新的白盒分组密码的设计与分析,同时基于物理不可克隆函数(PUF)设计了一种白盒方案。
区别于基于查找表设计的白盒实现,基于自等价编码设计的白盒实现作为一种新型的白盒实现方式值得深入研究。RANEA等[13]总结了自等价编码设计白盒实现的局限性、白盒方案的编码空间和适用范围受到的限制。笔者对RANEA等的方案进行了改进,基于扩大编码空间的思路提出了两种改进方案,并对改进后的方案进行了安全性分析。分析表明,改进后的方案可以抵抗RANEA等提出的通用攻击,同时基于改进方案设计的4 bit小型S盒的白盒方案的安全性也得到了提高。最后基于改进的方法设计了白盒AES,并与原方案进行了对比,证明了改进设计的安全性结论。
1 基于自等价编码的白盒实现
在设计白盒方案前,先介绍自等价的相关知识。自等价是从BIRYUKOV等[25]提出的线性/仿射等价算法延伸出的概念。
定义1(线性/仿射等价[25]) 若S1、S2为两个m比特变换的S盒,存在一对m比特的线性/仿射置换(A,B),使得S2=B∘S1∘A,则称S1和S2是线性/仿射等价的。
定义2(线性/仿射自等价[25]) 若S为m比特的S盒,存在一对m比特的线性/仿射置换(A,B),使得S=B∘S∘A,则称(A,B)为S的一个线性/仿射自等价。其中,A为右自等价,B为左自等价。
记SE(S)为S的全体自等价构成的集合,RSE(S)为S的全体右自等价构成的集合,LSE(S)为S的全体左自等价构成的集合。
基于自等价编码的白盒实现[13]的思想是将SPN密码的密钥与线性层结合成仿射层,并使用随机选择的S盒的自等价对仿射层进行编码保护,具体步骤如下。
步骤1 对SPN密码的轮函数进行拆分、重组。将SPN密码的轮函数表示为E(r)=LL∘SL∘⊕k(r),LL为密码的线性层,SL=S1‖S2‖…‖Sρ为密码的S盒层,k(r)为第r轮的轮密钥。将当前轮的LL与下一轮的k(r)结合为仿射层,即AL(r)=⊕k(r)∘LL。将SPN密码表示为仿射层与S盒层交替,如图1所示。第1轮和第nr+1轮的仿射层分别定义为AL(1)=⊕k(r)和AL(nr+1)=LL。
步骤2 使用S盒的自等价对仿射层进行编码:
(1)
由于自等价的特性,编码后的仿射层与S盒交替时,中间加入的自等价编码能被抵消,如下所示:
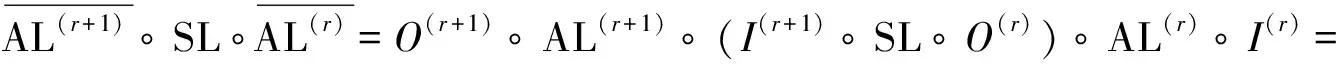
(2)
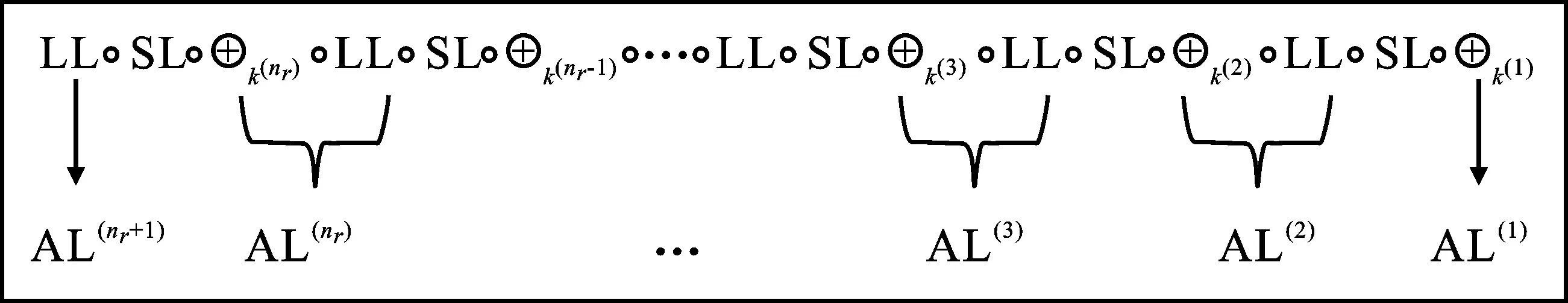
图1 SPN密码的加密过程
白盒方案需要加入外部编码,防止代码提取攻击。因此,在算法外需要加入外部编码,加入外部编码后的白盒实现E′k形式如下所示:
(3)

图2 原方案的仿射层编码

该方案一方面利用自等价的特性使得白盒实现方案与原算法在功能上保持一致,另一方面不需要使用查找表技术,并且S盒不需要保护,因此内存占用空间大大减小,是一种新型的白盒实现。基于上述介绍的白盒实现方案,RANEA等提出了以下两类仿射等价问题,用于讨论方案的安全性。
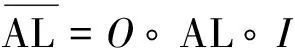
(4)
其中,Lin(g)表示取仿射函数的线性部分。Lin(Oi)作为该问题的一个特解,解集为Lin(Oi)∘(C(L)∩ Lin(RSE(Si))),其中C(L)称为L的中心化子集合,即C(L)={A∈GLn:A∘L=L∘A},GLn为包含所有n比特线性置换的一般线性群,Lin(RSE(Si))表示Si右自等价的线性部分集合,C(L)∩Lin(RSE(Si))表示上述两个集合取交集。
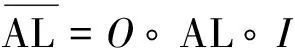
(5)
该问题包含一个特解(X0,Y0),其中Lin(X0)=Lin(Oi)。特别地,该问题的解(X,Y)中,X满足
Lin(X)=Lin(Oi)∘( Lin(LSE(LLi,j∘Sj)) ∩ Lin(RSE(Si))) 。
(6)
在文献[13]中可看到关于这两个问题的证明。
2 改进的自等价编码白盒方案
笔者对RANEA等[13]的自等价编码的白盒方案进行分析,发现白盒方案的编码空间依赖于原SPN密码的S盒的性质,且针对4 bit的小型S盒设计的自等价编码的白盒方案安全性不够理想。因此,笔者基于扩大编码空间这一思路提出了两种改进方案。
2.1 改进方案1
将原S盒的自等价与线性层的自等价结合为仿射层新的输入输出编码,可分为以下两步进行。
步骤1 找到n比特的可逆矩阵P和Q,使得LL=Q∘LL∘P,其中LL为SPN密码的线性层,表示为n×n比特的变换。因为LL是可逆的,所以对于随机选取的每一个可逆矩阵P,都可通过计算Q=LL∘P-1∘LL-1得到对应的可逆矩阵Q。
步骤2 将S盒的自等价级联为S盒层的自等价I=I1‖I2‖…‖Iρ,O=O1‖O2‖…‖Oρ,并与线性层自等价P和Q结合。其中,单个S盒Si为m比特的变换,i=1,…,ρ,n=m×ρ。

图3 改进方案1的仿射层
2.2 改进方案2
在原方案仿射层的外部加入线性编码,并与S盒自等价编码结合为仿射层新的输入输出编码;同时在进入S盒层前解码,保证加入的线性编码能抵消,可分为以下两步进行。
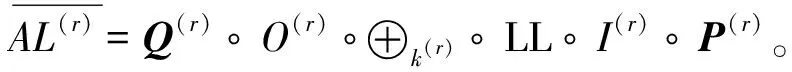
步骤2 在S盒层加入编码,起抵消仿射层线性编码的作用,定义加入编码的S盒层为TL,TL=P-1∘SL∘Q-1,其中第r轮编码的S盒层可表示为TL(r)=(P(r+1))-1∘SL∘(Q(r))-1。
考虑相邻两轮的轮函数,可以看到在相邻轮中加入的自等价编码和线性编码可以相互抵消,从而该白盒实现方案未改变原算法的功能,如下所示:
Q(r)∘O(r)∘AL(r)∘I(r)∘P(r)=
Q(r+1)∘O(r+1)∘AL(r+1)∘SL∘AL(r)∘I(r)∘P(r)。
(7)
改进方案2中某一轮的仿射层如图4所示。
3 安全性分析
为了分析自等价实现方案的安全性,RANEA等[13]提出了一种通用攻击。攻击思路是基于线性/仿射等价问题,将编码空间归约到该仿射等价问题的解集上,减小了仿射层输出编码的空间;进而再通过穷举搜索和使用密钥扩展排除错误的可能,恢复出密钥。减小轮编码空间的步骤分为两步。
RANEA等[13]指出:对于任何SPN结构密码算法的自等价实现方案,中心化子问题和非对称问题是通用的等价问题,但对于其他的自等价有特殊结构的密码,也存在其他的等价问题,进而可以利用这些问题进行归约攻击。
笔者通过建立中心化子问题和非对称问题,尝试对改进方案进行分析。分析的具体结果如下。
3.1 改进方案1的安全性分析
(1) 基于中心化子问题的归约攻击。首先将改进方案1仿射层的线性分块表示为
(8)

(P-1)j,i∘(LL-1)j,i∘(Q-1)j,i∘Lin(Oi)-1=
(9)
由于P和Q是n×n比特的可逆矩阵,它们的分块矩阵Pi,j,Qi,j不一定可逆,中间项Pi,j与(P-1)j,i无法抵消,不能将其视作中心化子问题,自然无法将编码空间归约到线性层分块的中心化子问题。因此,改进方案1可以抵抗基于中心化子问题的攻击。
(2) 基于非对称问题的归约攻击。该问题利用了自等价的特性,即一轮仿射层的输出编码、S盒、下一轮仿射层的输入编码相结合时,不改变S盒的输入输出,即
(10)
成立,则存在常数c使得
(11)

3.2 改进方案2的安全性分析
(1) 基于中心化子问题的归约攻击。首先,将仿射层的线性分块表示为
(12)
(13)
此时可以构造类似的中心化子问题:
(14)

(2) 基于非对称问题的归约攻击。在改进方案2中,编码后的S盒层TL=P-1∘SL∘Q-1。根据式(10),可得
(15)
将仿射层的线性部分与编码后的S盒结合:
(16)
记S′=(P-1)j∘Sj∘(Q-1)j,即S′为被编码的S盒。根据式(16),可建立非对称问题:
(17)
其中,Lin(X)∈GLm∘Lin(RSE(Si))。
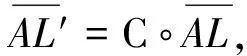
与基于中心化子问题进行归约攻击的结果类似,分块编码空间的大小由|GLm∘RSE(Si)|变为|RSE(Si)-1∘GLm∘RSE(Si)∘(Lin(LSE(LLi,j∘Sj))∩(GLm∘Lin(RSE(Si))))|。最终的归约结果未减小分块编码空间,因此改进方案2可以抵抗基于非对称问题的归约攻击。
3.3 分析总结
与RANEA等的方案相比,这两种改进方案分别通过在线性层和仿射层外部加入线性编码的方式,在一定程度上扩大了归约后的编码空间的大小。加入线性编码后,改进方案1可以抵抗基于中心化子问题和非对称问题的攻击;改进方案2使得归约没有效果,从而也可以抵抗基于中心化子问题和非对称问题的攻击。可以看到,线性编码的存在大大提高了方案抵抗攻击的能力。
4 基于改进方案设计的白盒AES及安全性分析
基于上述两种改进方式对文献[13]中的白盒AES进行改进。笔者给出了两种改进方案,并进行了安全性分析,最后与原白盒AES进行了对比。
4.1 方案设计
步骤1 计算AES的S盒自等价结构和数量[25]。
AES的S盒的代数表达式为S(x)=Ax-1⊕c,即先对x取GF(28)上的乘法逆元,再作用一个固定仿射函数。可以将常数c与轮密钥结合,考虑S(x)=Ax-1。记Pd为GF(28)上的8 bit函数,定义Pd(x)=xd,因此可以得到S(x)=A∘P254(x)。定义GF(28)上的函数Mα(x)=α×x,其中α∈GF28,“×” 表示GF(28)上的模多项式乘法,模多项式为f(x)=x8+x4+x3+x+1。文献[25]中计算出S盒的自等价表达式为如下形式:
(18)
由于α有255种选择,i有8种选择,因此AES的S盒自等价有255×8=2 040种选择;且从自等价的表达式可以看出,左右自等价均为线性自等价。
步骤2 对仿射层添加S盒的自等价编码。
为了便于解释,忽略AES轮函数中的行移位操作。记线性层LL为列混合操作对其中的一列进行的变换,对LL进行分块:
(19)
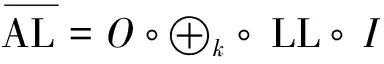
步骤3 分别按照第2节中改进方案1和改进方案2的步骤,选取可逆矩阵P,Q与S盒的自等价结合,作为仿射层的输入输出编码。
两种改进方案如下。
(1) 采用改进方案1的设计,白盒AES的仿射层表示为
(20)
(2) 采用改进方案2的设计,白盒AES的仿射层与S盒层分别表示为
(21)
TL=P-1∘(S1‖S2‖S3‖S4)∘Q-1。
(22)
改进方案1使用随机选择的可逆矩阵对线性层进行编码,由于P和Q是线性层LL的自等价,因此编码后的仿射层仍与AES算法的功能保持一致;改进方案2对加入S盒自等价的仿射层进行线性编码,同时对S盒进行编码,用来抵消仿射层的输入输出编码。
4.2 安全性分析
考虑用RANEA等提出的通用攻击来分析基于上述改进方案设计的白盒AES,攻击思路是对AES轮编码的线性部分建立线性/仿射等价问题,通过构造新的仿射层编码,将编码空间归约到等价问题的解集上。方案的安全性依赖于这个更小的编码空间的基数。下面通过对AES构造中心化子问题和非对称问题,对O1这一分块编码空间进行归约并分析归约效果。
1) 原白盒AES的安全性[13]
RANEA等基于中心化子问题,将分块编码空间的大小从|RSE(S)|减小到|{Mα:0≠α∈GF(28)}|,即从2 040减小到255;基于非对称问题,可将分块编码空间的大小从|{Mα:0≠α∈GF(28)}|减小到|(LSE(S)∩{Mα:0≠α∈GF(28)})|。
2) 白盒AES改进方案1的安全性

由于P,Q为随机选择的32 bit可逆矩阵,构造
(23)
因为P和Q未知,且它们的分块矩阵不一定可逆,因此无法得到中心化子问题,从而在这种情况下,改进方案1的白盒AES能抵抗基于中心化子问题的归约攻击。

3) 白盒AES改进方案2的安全性

通过对改进方案2的仿射层线性部分进行分块,可以得到
(24)
根据式(24)建立中心化子问题:
(25)
其中,X0=Q1∘O为该问题的一个特解,问题的解集为GL8∘O1∘(C(M3)∩(GL8∘RSE(S)))。根据节3对改进方案2的分析,分块编码空间的大小从|GL8∘RSE(S)|变为|RSE(S)-1∘GL8∘RSE(S)∘(C(M3)∩(GL8∘RSE(S)))|,即最终的归约结果并没有减小分块编码空间。因此,改进方案2可以抵抗基于中心化子问题的归约攻击。
因为编码后的S盒层为TL=P-1∘SL∘Q-1,将仿射层的线性部分与编码后的S盒结合,如下所示:
(26)
记S′=(P-1)3∘S∘(Q-1)3为被编码的S盒,根据式(26)可建立非对称问题:
(27)
其中Lin(X)∈GL8∘RSE(S)。
该非对称问题关于X的一个特解X0满足Lin(X0)=Q1∘O1,关于X的解集满足Lin(X)=GL8∘O1∘(LSE(S)∩(GL8∘RSE(S)))。根据节3的分析,分块编码空间的大小由|GL8∘RSE(S)|变为|RSE(S)-1∘GL8∘RSE(S)∘(LSE(S)∩(GL8∘RSE(S)))|。最终的归约结果未减小分块编码空间,因此改进方案2可以抵抗基于非对称问题的归约攻击。将两种白盒AES的改进方案与原白盒AES进行比较,如表1所示。

表1 两种改进的白盒AES与原白盒AES安全性比较
从表1可以看到,两种改进方案均扩大了分块编码空间,并在基于中心化子问题和非对称问题的归约攻击下,改进方案1可以抵抗两种攻击,改进方案2使得归约没有效果,从而都增强了方案抵抗攻击的能力。
5 结束语
通过添加线性编码来扩大仿射层编码空间,笔者对基于自等价编码的白盒实现进行了改进,给出了两种改进方案,并进行了安全性分析。分析表明,两种改进方案均增大了输入输出编码的取值空间,同时两种方案均增大了归约后的编码空间的大小,均能抵抗针对自等价编码的白盒实现的通用攻击。最后,笔者基于这两种改进的设计方法构造了两种AES的白盒实现,并与原方案进行了对比。安全性比较结果证明了上述的分析结论。
