基于数学推理的情境教学策略

郭力丹

数学是一门严谨性与逻辑性都很强的学科，数学知识内部存在着千丝万缕的关系，环环相扣、逐层推进。数学推理能力作为小学数学核心素养的重要内容，是解决问题的基本技能之一，更是学生今后学习和生活中所需要的重要的数学素养。因此，小学数学教师应关注学生推理能力的培育，并立足于学生的思维实际与教学内容的实际在课堂教学中给予渗透落实。笔者以为，可以通过多元的情境创设，助推数学抽象能力的提升。

一、创设认知冲突的情境，激发数学推理意识

心理学研究表明，学生思考的积极性和主动性往往来自于让他们能产生强烈认知冲突的情境。因此，教师要及时读懂学生在课堂中的思维困惑，根据教学内容的特点，巧妙地用问题来导引、点燃学生的思考。问题情境应能促使学生“触景生思”，将其置于一种“思而不达”的境遇，激发学生的数学推理意识。

例如，在教学“三角形内角和”时，笔者先是让学生用自己喜欢的方法自主探索各自手中的三角形三个内角的总度数。用量角器量并计算出三个内角的和后，有的学生汇报三角形的内角和是178°，有的学生汇报是181°，有的学生汇报是180°……当学生的答案不一致时，其思维处于一种强烈的认知冲突之境，产生了“三角形内角和是不是都约等于180°”这样的疑问。于是，笔者相机追问：“三角形内角和到底是约为180°，还是等于180°？”学生的认知冲突被提升到了一个新的高度，急切想探个究竟。于是，有的学生兴奋地发现：“三角形的内角和就是180°。”笔者让这位学生有条有理地说说理由，只见学生是这样推理的：“将这个三角形的三个角‘折’在一起（边说边动手折），就拼成了平角，因为平角是180°，所以这个三角形的内角和就是180°。”笔者故意不及时评价，环顾四周，让其他学生来评价。接着，学生纷纷按这个方法动手操作验证，并将推理简述成“三个角拼成一个平角，平角是180°，所以三角形的内角和是180°”。这时，又有一学生惊讶地发现：“老师，我不用折，而是把三个角都撕下再‘拼’，也得出了一个平角，也得出三角形内角和是180°。”还有一个学生发现：“我不用折，也不用拼，而是用画的方法，看！随便拿一个内角和是360°的四边形沿对角一画，这样每个三角形内角和是180°。”正是让学生思维处于一种认知冲突的困扰之中，有效地点燃了他们思维的火花，学生自主地找到打开“困惑”的钥匙，学会用“因为……所以……”进行推理，数学推理在“润物细无声”中得以激发并培育。

二、搭建思辨說理的情境，掌握数学推理方法

对于还是以直观形象思维为主的小学生来说，在数学推理的过程中，为保证其思维过程的清晰，应给他们搭建充分的思辨说理的情境，让学生通过相互间的讨论来支撑自己的想法，在讨论之中检验其正确性，找到最为简便、有条理的推理方法。

例如，在教学“大数的认识”后，教师编排了一节综合实践活动课。课始，教师提出了这样的问题：“1亿张纸摞在一起会有多高？”有部分学生并没有养成严谨的数学推理的习惯，而是随意猜测说出“15 米”“20米”“100米”等答案，这些答案显然毫无理由与根据。这时，教师可以继续引导：“1亿张纸摞在一起会有多高，这不是在猜谜语，而应该用数学方法有理有据地进行推理，你能想到什么方法？”有学生马上质疑，表示：“老师，我们没有1亿那么多纸张来摞”“就算有1亿张纸张，摞起来也要好长时间呢”等。正当学生处于一种悱愤的思维状态之时，教师引导学生以小组的形式一起讨论如何解决问题。有位小组代表这样说：“我们小组认为不用拿1亿张纸张，只需要用100张纸摞在一起量出是多高，就可以推理出1亿张纸的高度了。”话音刚落，教室里掌声四起。学生动手量出了100张纸的高度是1厘米之后，教师让学生试着推理出“1亿张纸的高度”。这时，学生能有理有据地进行这样的推理：“100张是1厘米，1000张就是1分米，10000张就是1米，而1亿里有10000个10000，所以1亿张纸就是10000米，也可以说是10千米。”这样的教学，将学生的思维置于一种思辨说理的轻松、和谐的课堂氛围中，让学生实现从“随意猜测”到“有条理推理”的提升，找到合理的推理方法，推理得出了 “1亿张纸摞在一起有10千米高”的正确结论，促使学生的数学推理能力得以发展。

三、设置灵活变式的情境，锻炼学生推理能力

数学推理能力的培养重在让学生能有理有据地按一定的方法、程序进行推理。教师要关注课堂教学素材的丰富性，让学生能真正建构概念，为数学推理储备扎实的理论支撑;还要关注课堂练习设计的变式，让学生的数学推理能力能得以锻炼。教师可充分利用变式，多呈现一些灵活的题型，让学生能感知多种解决问题的背景、适用条件和可能，从而不断锻炼学生的推理能力。

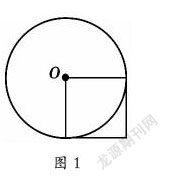
例如，在教学完“圆的面积”后，几乎全部学生都能掌握圆的面积公式“S圆=πr2”，并能正确使用这个公式解决有关于圆的面积的一些实际问题。然而，大多的练习只是停留于提供圆的半径、直径或是周长，让学生通过先求出圆的半径再运用公式进行解决。长期进行这样的练习，学生只是停留于低阶思维层面上的推理，这不但会让学生形成不良的思维定式（即要算圆的面积必须得先算出半径，把半径当作是求圆的面积的必要条件），而且不能很好地锻炼学生的数学推理能力。基于这样的认知，笔者以为，可以进行如图1这样的变式设计，即“已知正方形的面积是4平方分米，求圆的面积”，促使学生调用已有的知识经验来解决。学生发现：要求圆的面积得先求出半径，然而半径就是正方形的边长，从而再推理要先算正方形的边长，需要对4平方分米进行开平方，这显然已经超出了学生的经验。这样，学生就不得不绞尽脑汁另辟路径。将学生的思维设置到一种“变式场域”中，激发学生不断地寻找解决问题的路径，从而促使学生推理发现：正方形的边长就是圆的半径，而因为S正=r2=4（平方分米），所以可以直接将r2=4代入到圆的面积公式，得出了S圆=πr2=3.14×4=12.56（平方分米）。至此，学生能进行灵活地推理，能换个角度推算出圆的面积。长期进行这样的练习，可以很好地发展学生的数学推理能力。

总而言之，数学是一门锻炼学生思维的学科，若要促使学生从直观形象思维走向抽象逻辑思维，应当从培养推理能力开始。小学阶段是培养学生推理能力重要时期，教师要善于创设各种情境，引导学生进行数学推理，从而培养学生数学核心素养。

（作者单位：福建省福州市鼓楼第二中心小学）