斜齿圆柱齿轮车齿加工数学模型与齿面误差分析

王长健，曹雪梅，许 浩，魏冰阳，何宏图，张新成

(1.河南科技大学 机电工程学院，河南 洛阳 471003；2.中南传动机械厂，湖南 长沙 410200)

0 引言

双联齿轮、人字齿轮具有结构紧凑等特点，广泛运用于机床、汽车变速箱内。由于双联齿轮、人字齿轮退刀槽太小，加工空间受限制，如采用滚齿加工，滚刀容易与另一侧齿轮发生干涉。车齿加工[1]是车齿刀两条切削刃沿齿向切削的加工方法，可通过设计刀具螺旋角度来满足不同加工需求，从而消除双联斜齿圆柱齿轮与刀具干涉问题。

车齿加工技术具有高效、高精度等优点，比插齿效率高3～5倍[2]。文献[3]分析了车齿刀刃曲线与被加工齿轮双自由度的相对运动。文献[4]利用给定刀具、齿轮厚度和工艺数据，仿真验证了车齿特征工艺值。文献[5-7]基于双自由度曲线与曲面包络理论，分析了车齿刀具前角、后角和刀具运动偏心对齿形误差的影响。文献[8]对车齿刀具运动产生的偏差导致齿面波纹进行分析，提出改善工件齿面波纹的刀具齿数设计方法。文献[9]建立了内齿圈刮齿数学模型和误差数学模型，分析了机床调整参数引起的齿形误差。文献[10]利用线性叠加原理和线性回归方法提出机床参数修正方法。

综上所述，国内外学者大多采用斜齿刀加工直齿或直齿刀加工斜齿[11-12]，少见对斜齿刀加工外斜齿轮进行研究。基于运动学建立啮合方程，推导过程比较复杂。本文建立斜齿刀具与斜齿圆柱齿轮车齿展成加工数学模型，基于微分几何建立啮合方程，并进行切齿加工试验与齿面检测。

1 车齿加工原理

车齿加工基于交错轴齿轮啮合原理[13],车齿加工模型如图1所示。车齿刀和工件绕各自轴线按照一定的滚比转动，刀具角速度为ω1，工件角速度为ω2；工件沿轴向做进给运动，位移量为l2。

车齿加工运动示意图如图2所示。图2中，β1为刀具螺旋角；β2为工件螺旋角；∑为刀具轴与工件轴的轴交角，大小如表1所示。左旋车齿刀加工右旋圆柱外齿轮，若车齿刀具旋向与工件旋向相同，轴交角为两者之和的绝对值；若刀具与工件旋向相反，轴交角则为两者之差的绝对值。内齿轮与其相反。

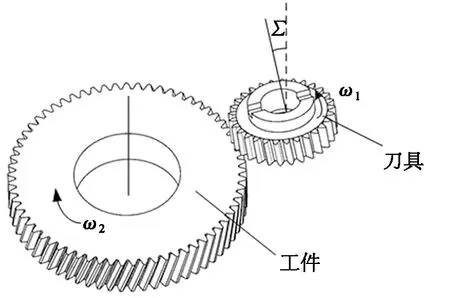
表1 车齿加工轴交角

车齿加工直齿圆柱齿轮时，刀具与工件的角速度关系为：

(1)

其中：φ1、φ2分别为刀具、工件转角；Z1、Z2分别为刀具、工件齿数。

当加工斜齿轮时，刀具与工件之间需要一附加转角保证加工出正确螺旋角，其关系为：

(2)

其中：mn为工件法向模数。对于外齿轮，刀具旋向与工件旋向相同为+，相反为-；内齿轮则相反。

2 车齿加工模型

2.1 刀具模型

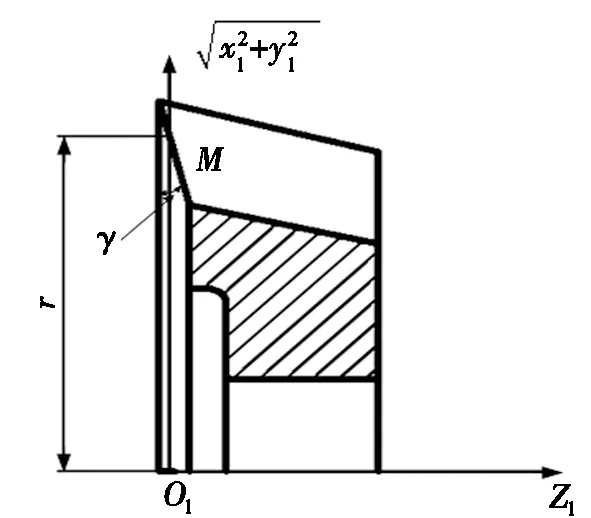
图3 圆锥面刀具前刀面截面示意图

车齿刀前刀面有球面、平面、锥面等多种类型[14]，本文建立锥面车齿刀具模型。

图3为圆锥面刀具前刀面截面示意图。r为刀具的分度圆半径；Z1轴与刀具轴线重合；原点O1通过刀具轴线，并位于刀具前刀面分度圆处在Z1轴的投影；M为前刀面上任意点，其纵坐标为旋转投影面到轴线距离，横坐标为齿宽方向Z1值；γ为刀具前角，由几何关系可得：

(3)

其中：(x1,y1,z1)为刀具齿面点的坐标。

前角为零时，车齿刀刃形曲线为渐开线[15-16]：

(4)

其中：rb为刀具基圆半径；u为渐开线变量。则刀刃曲线方程为：

r0=[x0(u),y0(u),z0(u)]T。

(5)

车齿刀为左旋斜齿轮，刀刃绕自身轴线转动角度为θ，刀刃自身沿刀具轴线z1方向移动dl，其坐标变换关系为：

(6)

其中：

(7)

则斜齿车刀方程表示为

r1(u,dl)=M1r0(u)，

(8)

其中：变量dl可由前刀面方程式(3)作为约束条件消去。

2.2 车齿展成加工数学模型

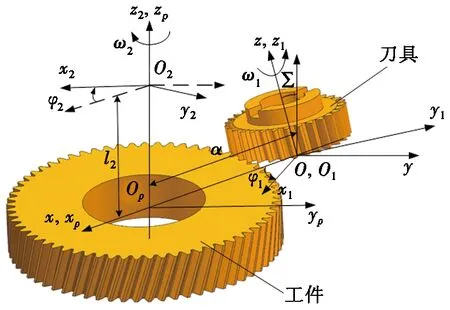
图4 车齿展成加工坐标系

图4为车齿展成加工坐标系，S(O-xyz)为固定坐标系，与刀具初始位置重合，S1(O1-x1y1z1)坐标系为刀具运动坐标系，刀具回转轴中心为z1轴，与z轴重合，以角速度ω1绕z1轴旋转，角度为φ1。Sp(Op-xpypzp)为辅助坐标系，与工件初始位置重合，原点Op位于工件端面圆心，S2(O2-x2y2z2)与工件固连，z2轴为工件旋转中心，与zp轴重合，z1轴和z2轴之间的夹角为∑，工件以角速度ω2绕z2轴旋转，旋转角度为φ2。x轴和xp轴重合，点OOp的距离为中心距a。车齿加工时，刀具与工件按照滚比转动，同时工件沿z2轴向移动，距离为l2。

由刀具运动坐标系r1推导出工件运动坐标系r2，其空间坐标变换关系为：

r2(u,l2,φ1,dl)=M2PMPOMO1r1(u,dl)，

(9)

其中:

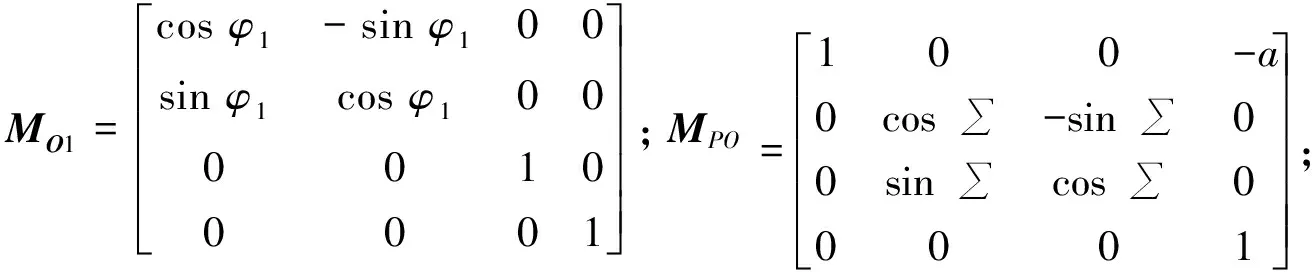
2.3 微分几何法建立啮合方程

车齿加工切削刃展成齿面。车齿刀在展成过程中不仅有绕自身轴线的转动，还有沿轴线的移动和被加工工件的转动，具有两个独立运动自由度。

偏导矢∂r2/∂u和∂r2/∂l2表示在工件动系S2(O2-x2,y2,z2)齿面上两条不同方向的切线[17]，两者的向量积为齿面法矢N1，φ1为广义运动参数，对三变量(u,l2,φ1)求偏导矢建立啮合方程：

(10)

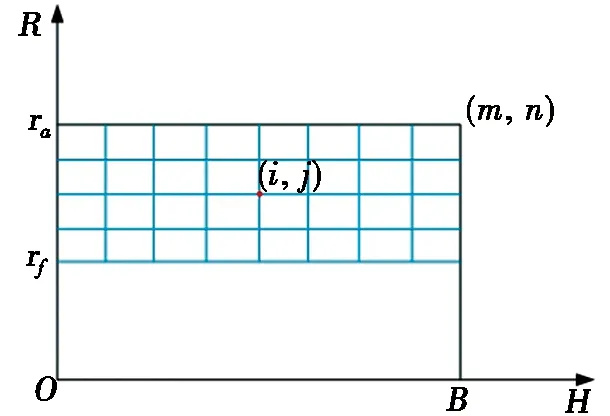
图5 工件网格节点

工件网格节点如图5所示，在工件旋转投影面上划分网格节点[18]。图5中，R为工件旋转投影面齿高方向的纵坐标，H为投影面齿宽方向的横坐标，ra为工件的齿顶圆半径，rf为齿根圆半径，B为工件齿宽。沿齿宽方向取m个节点，齿高方向取n个节点，建立旋转投影面位置方程。

(11)

其中：[x2(ij),y2(ij),z2(i)]T为工件齿面节点。

将式(3)、啮合方程(10)与位置方程(11)联立求解，得到齿面点坐标。

2.4 车齿理论齿面与标准渐开线螺旋面对比

为了比较车齿理论齿面与标准渐开线螺旋面偏差，需要对车齿理论齿面进行角向定位，使其与标准渐开线螺旋面在基准点重合[19-20]。选取工件分度圆与齿宽中线的交点为基准点[xk,yk,zk]T，旋转标准渐开线螺旋面，旋转角度ψ1满足：

-xksinψ1+ykcosψ1=0。

(12)

同理，计算出车齿理论齿面在基准点的坐标值[x2m,y2m,z2m]T，求得旋转角度ψ2满足：

-x2msinψ2+y2mcosψ2=0。

(13)

再根据投影面上的位置点(Rij,Hij)，求得标准渐开线螺旋面对应的点坐标[xk(ij),yk(ij),zk(ij)]T，旋转ψ1角度得到:

(14)

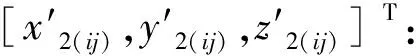
(15)

车齿理论齿面与标准渐开线螺旋面任一点的误差值为：

(16)

3 算例

3.1 车齿刀具与齿轮参数

采用左旋斜齿刀加工双联右旋斜齿齿轮，两齿轮间退刀槽为10 mm，小齿轮采用车齿加工，刀具与工件基本参数见表2。

表2 刀具与工件基本参数

3.2 车齿理论齿面误差分析

图6是刀具螺旋角为5°时，车齿理论齿面与标准渐开线螺旋面的对比图。由图6可以看出：车齿理论齿面主要为齿廓偏差，在齿根处最大偏差为0.069 μm，齿顶处最大偏差为0.022 μm。

图6 车齿理论齿面与标准渐开线螺旋面的对比图

刀具螺旋角对齿廓偏差的影响如图7所示。由图7可以看出：刀具螺旋角为0°(直齿刀)时，车齿加工没有齿廓偏差，随着刀具螺旋角的增加，车齿理论齿面与标准渐开螺旋面齿廓偏差增大，刀具螺旋角为9°时偏差最大，为0.104 μm；随着刀具螺旋角继续增大，偏差逐渐减小，刀具螺旋角为18°时，与刀具螺旋角0° 一样时，没有齿廓偏差，此时轴交角为零，相当于两个斜齿轮啮合。结果表明：刀具螺旋角大小直接影响工件齿廓偏差。

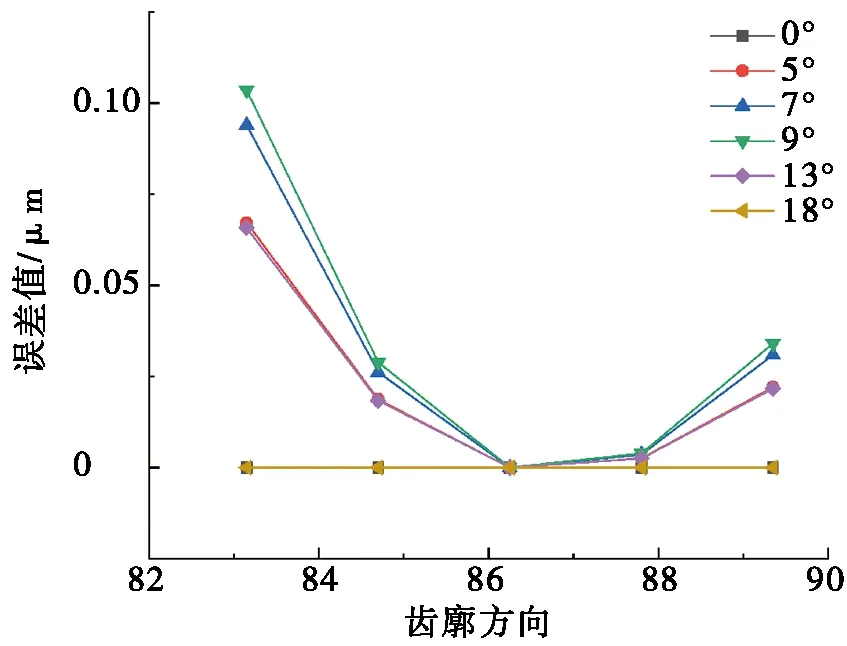
图7 刀具螺旋角对齿廓偏差的影响

4 车齿加工及齿面检测

车齿加工试验采用洛阳科大越格机床厂生产的YK2260NC数控车齿机，斜齿轮车齿加工如图8所示，基本参数见表2，刀具转速为500 r/min。

在Gleason 650GMS检测中心检测齿轮精度，如图9所示。图10为实际车齿齿面与标准渐开线螺旋面的齿面误差图。左齿面最大偏差值为9.983 μm，右齿面最大偏差为9.093 μm。

沿齿轮一周抽取1号、17号、33号、49号齿左右齿面进行检测。表3为左右齿面齿廓总偏差。由表3可知：左齿面齿廓偏差Fα均值为8.6 μm(7级精度)，右齿面齿廓Fα偏差均值为7.0 μm(7级精度)。表4为左右齿面螺旋线总偏差。由表4可知：左齿面螺旋线总偏差Fβ为5.2 μm(6级精度)，右齿面螺旋线总偏差Fβ均值为4.6 μm(6级精度)。

产生误差的原因主要是刀具的固有误差[21]，刀具在制造过程也存在一定误差，并不一定是标准的渐开线，刀具固有的误差也会映射到工件齿面；另外，机床本身存在一定运动精度问题，但在误差要求范围内，均能满足生产需要。试验表明，齿廓偏差和螺旋线总偏差均能满足加工需要。

表3 左右齿面实测齿廓总偏差表

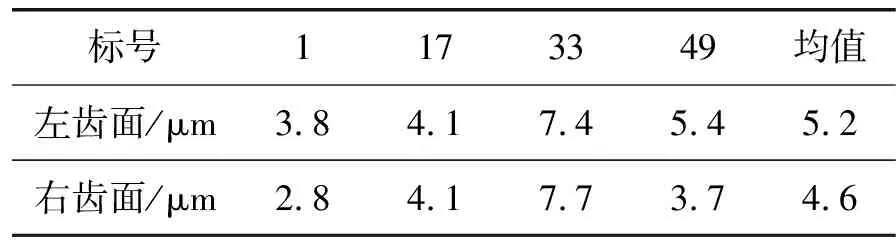
表4 左右齿面实测螺旋线总偏差表

5 结论

(1)本文按照双自由度曲线与曲面共轭原理推导斜齿圆柱齿轮车齿数学加工模型，运用微分几何方法建立啮合方程，该方法适用范围更广。

(2)建立车齿理论齿面与标准渐开线螺旋面偏差模型，比较了理论齿面与标准螺旋面的偏差，分析了不同刀具螺旋角对工件齿形的影响。随着刀具螺旋角的增大，齿形误差先增大再减小，只有零前角标准渐开线直齿刀才能加工出标准渐开线齿轮。

(3)在测量中心检测工件齿面的误差，工件左齿面齿廓偏差均值为8.6 μm，螺旋线总偏差均值为5.2 μm；右齿面齿廓偏差均值为7.0 μm ，螺旋线总偏差均值为4.6 μm，工件加工等级为7级，可满足生产需要。