油管模型建立及结构对称性对其残余应力影响

2022-05-25余光伟谢清程杨珺柳施睿赟蔡翔宇李文海

焊接学报 2022年3期

余光伟，谢清程，杨珺柳，施睿赟，蔡翔宇，李文海

(1.上海大学,上海,200444；2.上海船舶设备研究所,上海,200031)

0 序言

可调螺距螺旋桨(controllable pitch propeller，CPP)是一种船舶特种推进装置，其桨叶能够相对于桨毂转动[1].CPP 以其操纵性强、机动性高、寿命长、节省机舱空间等优点，已在特种船舶、军用舰艇等海上航行设备获得了广泛的使用[2].

为降低油管与传动轴之间的过度磨损和粘着，CPP 传动轴内安装的油管采用的是异种金属焊接结构.与同种金属的焊接结构相比，异种金属焊接结构更能发挥不同材料的优势[3]，结构轻量化、强度不一致性等需求推动了异种金属焊接的发展[4-8].在焊接的过程中，焊接接头产生残余应力是不可避免的.焊接残余应力是造成各种焊接缺陷的重要因素，也是焊接热应变脆化的根源，对焊接接头的疲劳寿命有显著影响[7].因此，准确地分析异种金属焊接件的应力对于提高焊接结构的制造质量和服役性能具有非常重要的意义[9-12].

自Ueda 等人[13]提出用热-弹-塑性有限元模型来计算焊接的残余应力与变形以来，焊接数值模拟得到了飞速的发展，已经成为预测残余应力和焊接变形的常用工具.Bajpei 等人[14]通过有限元软件ANSYS 建立了AA5052/AA6061 异种铝合金薄板对接焊有限元模型，预测了焊接的瞬态温度、残余应力与变形，并通过试验验证了模型的准确性.Xia 等人[15]通过ABAQUS 对异种金属环焊缝焊接接头进行了热力耦合分析，并通过试验验证了该模型的正确性，在此基础上探究焊接顺序、焊接起收弧位置对焊接残余应力的影响.研究结果表明，由于材料性能的差异性，焊接接头两侧的残余应力分布并不是对称的.Balram 等人[16]基于有限元软件ANSYS 建立了AISI 316/ Monel 400 异种金属平板钨极惰性气体保护焊(tungsten inert gas welding，TIG焊)接头的有限元计算模型，通过红外热像仪捕捉了焊缝表面的温度分布，并使用X 射线衍射仪测量了试验平板的残余应力，有限元模拟计算结果与试验结果具有良好的一致性.

国内外学者在异种金属焊接数值模拟分析方面已经取得了突出的成就，不过对复杂焊缝结构的研究并不多，对管道多焊缝多板结构的研究更少.文中以某船用钢/铜异种金属焊接油管为研究对象，建立了油管热-弹-塑性有限元分析的模型，研究了油管模型简化方法以及结构对称性对残余应力的影响，为复杂焊缝结构残余应力有限元计算模型简化提供了思路，为改进油管焊接工艺提供参考.

1 试验方法

油管的外径150 mm，内径128 mm，长度为5 m，沿油管的圆周方向上均匀焊接4 根长度为500 mm的支撑条.油管的材料为20 钢，支撑条材料为QAL9-4 铝青铜，焊丝牌号为HS CuAl，采用手工钨极氩弧焊交流焊接.焊前，先用风动砂轮打磨坡口表面两侧20 mm 范围内直至露出金属光泽，去除待焊区的油污、水分、灰尘、氧化膜等杂物，并采用丙酮清洗待焊区.焊接工艺参数如表1 所示.

表1 油管焊接工艺参数Table 1 Welding parameters of pipe

采用X-350A 型X 射线应力测定仪来测量焊接油管表面9 个点的残余应力，其测点位置分布如图1 所示，测量结果如表2 所示.X 射线发射管管电压27.5 kV，管电流7.5 mA，测试方法为侧倾固定法，阳极靶材为CrK，衍射晶面为(211)，2θ角范围为150°～ 156°.

图1 残余应力测点位置分布(mm)Fig.1 Position of residual stress experiment

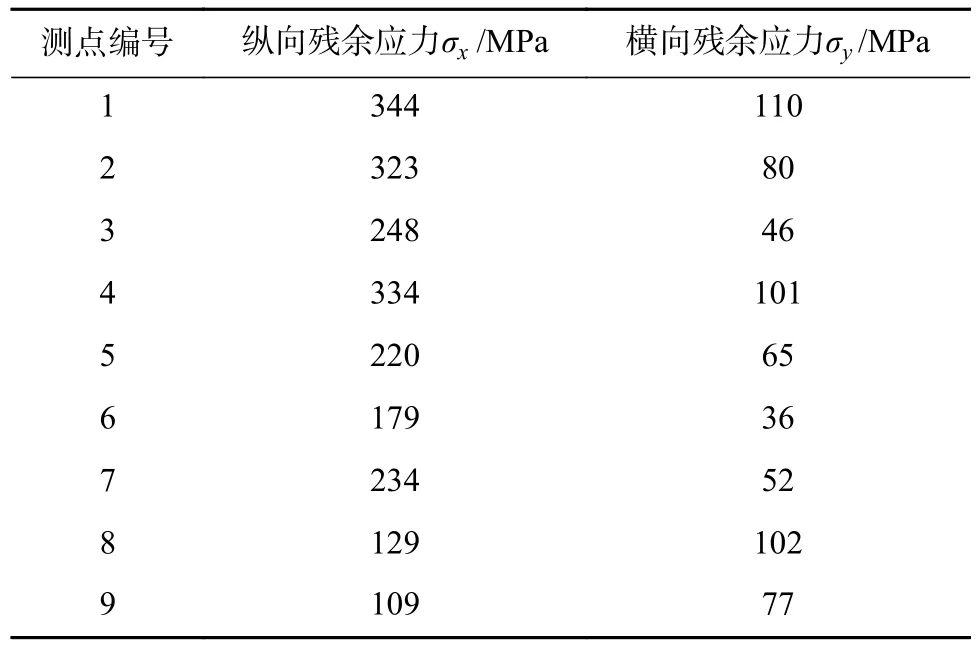
表2 油管测点残余应力Table 2 Residual stress of pipe

2 数值计算模型

2.1 有限元模型

建立如图2 所示的油管有限元计算几何模型.焊接时依次焊接支撑条1 到支撑条4.每根支撑条共有4 条焊缝，按照焊接顺序依次为焊缝1、焊缝2(长焊缝)和焊缝3、焊缝4(短焊缝).此模型长度为700 mm.支撑条的结构如图3 所示.长焊缝结构和短焊缝结构分别如图4 和图5 所示.

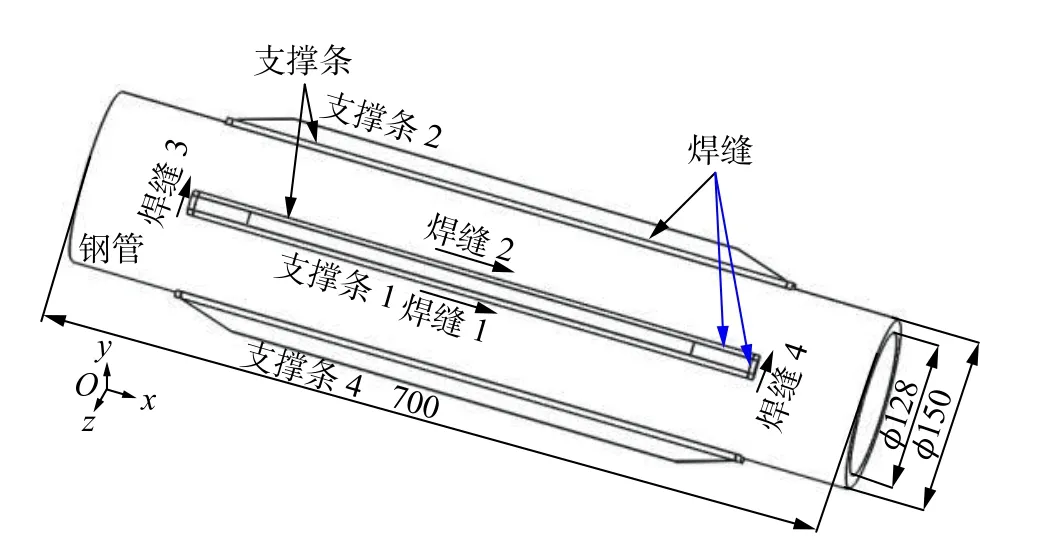
图2 油管几何模型(mm)Fig.2 Geometry of pipe

图3 支撑条结构(mm)Fig.3 Structure of support bar

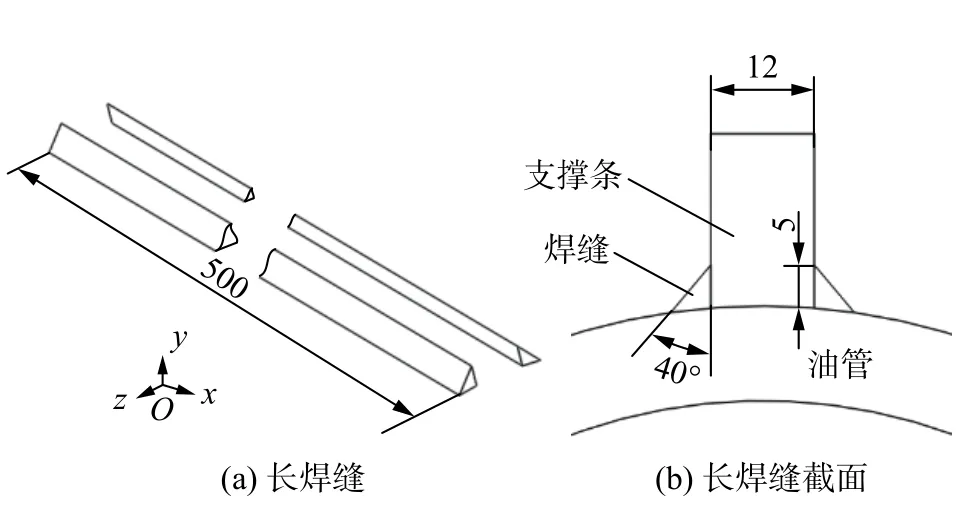
图4 长焊缝结构(mm)Fig.4 Structure of long weld.(a) long weld;(b) section of long weld

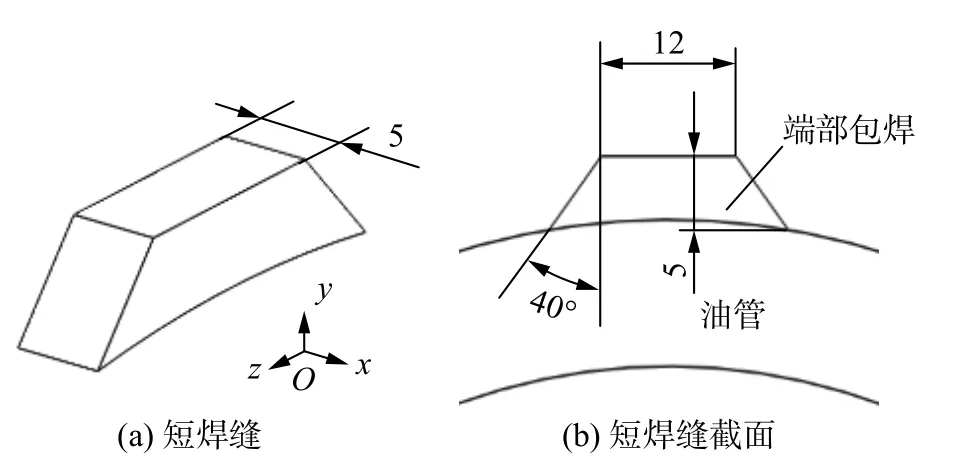
图5 短焊缝结构(mm)Fig.5 Structure of short weld.(a) short weld;(b) section of short weld

油管有限元模型如图6 所示，油管的节点总数为157 286 个，单元数量为126 712 个，温度场计算单元SOLID70，应力场计算单元类型为SOLID185.

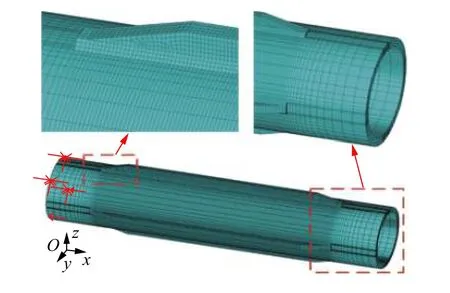
图6 油管有限元模型Fig.6 Finite element model of pipe

表3 为焊缝、支撑条和铝青铜QAl9-4 的化学成分.焊缝中Al 的含量略低于支撑条，Fe 的含量略高于支撑条，两者材料化学成分相近，因此有限分析中将焊缝与铝青铜看作为同一种材料.图7为20 钢和QAl9-4 铝青铜的热物理参数[17-19].文中考虑了熔池内流体的流动，在材料达到熔点温度后将材料的热传导系数假设为常温时候的2 倍[20].

表3 焊缝、支撑条及铝青铜QAl9-4 的化学成分(质量分数，%)Table 3 Chemical composition of weld,support and aluminum bronze QAl9-4

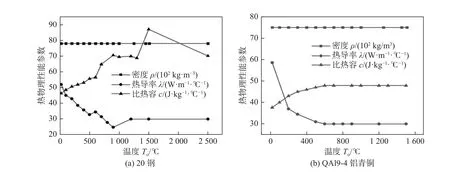
图7 热物理性能参数Fig.7 Thermal physical properties and model of heat source.(a) steel 20;(b) QAl9-4 aluminum bronze

2.2 温度场计算

在低碳钢的有限元分析中，固相相变对焊接变形和焊接残余应力的影响不大，所以文中忽略了固相相变[21]的影响.对于材料的液相相变潜热，通常有两种计算方式[22].第一种是在已知材料在相变前后的随温度变化的密度和比热容，可根据式(1)计算材料在不同温度下的热焓ΔH(T).

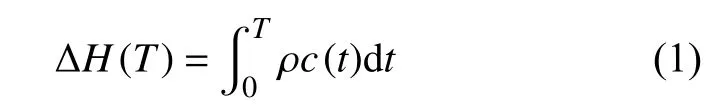
式中：ρ，c，T分别为密度、比热容和绝对温度；t为时间.

第二种是已知材料的相变潜热，可以采用材料等效比热法，即将材料的相变潜热等效考虑为材料的比热容，其计算公式[23]为

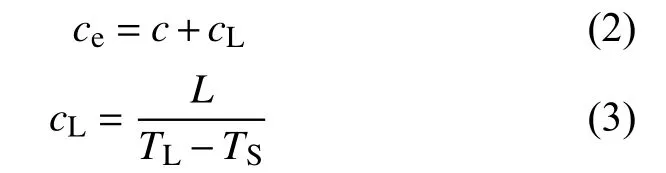
式中：ce为等效比热容；cL为液相比热容；L为相变潜热；TL为液相线温度；TS为固相线温度.将QAl9-4铝青铜的潜热转变为热焓，20 钢的相变潜热转换为等效比热容.20 钢从固相线温度1 450 ℃升温到液相线温度1 500 ℃时的相变潜热为270 J/kg[17-18].

Goldak 等人[24]发现在焊接过程中，因为电弧的运动使得熔池前面与熔池后面的能量分布是不一致，电弧后半部分的加热区域比前半部分的加热区域大.因此将焊接热沿着热源分为前半部分和后半部分椭球形状.xOy平面上为热流密度，xOy平面下为双椭球热源作用区域.双椭球热源的前、后半椭球的数学表达式为

式中：af，ar，b，c分别为双椭球的前半部分的长度、双椭球的后半部分的长度、熔池宽度参数、熔池深度参数，m；ff，fr分别为焊接热源的前、后能量分配系数；η为热源效率；U为电弧电压，V；I为焊接电流，A.文中焊接热源效率η为0.7，取ff=0.8，fr=1.2.各个形状的参数取值是相互独立的，常见的热源参数校核方法有：总结经验公式法、焊后熔池尺寸校核、软件校核等[25].文中通过对比有限元计算的熔池尺寸和试验测量的熔池来校核热源的形状参数设置的合理性.

图8 为油管的焊缝金相形貌.从图8 可以看出，铝青铜的熔合线深度与20 钢的熔合线的深度相接近.但铝青铜的熔点为1 037℃，20 钢的熔点为1 473℃，双椭球热源的热流密度是关于x轴对称的，因此在调整热源的形状参数时存在着这一问题，当调整双椭球的热源参数使得20 钢的熔合线与试验截面中20 钢的熔合线重合时，必然会导致有限元计算中铝青铜支撑条的熔合线过深.当热源参数符合铝青铜的熔合线时，有限元计算的20 钢熔合线又会比较浅.莫春立等人[26]指出当焊接异种材料时，可以将双椭球分成4 个1/8 的椭球瓣.文中根据当前的试验结果，将2 个1/4 椭球的Goldak 双椭球热源模型，调整为4 个1/8 的椭球的四椭球热源.修正后的四椭球热源模型熔池热源表达式(6)所示，其中xOy平面上为热流密度，xOy平面以下为热源作用区域.

图8 焊缝形貌Fig.8 morphology of welded seam

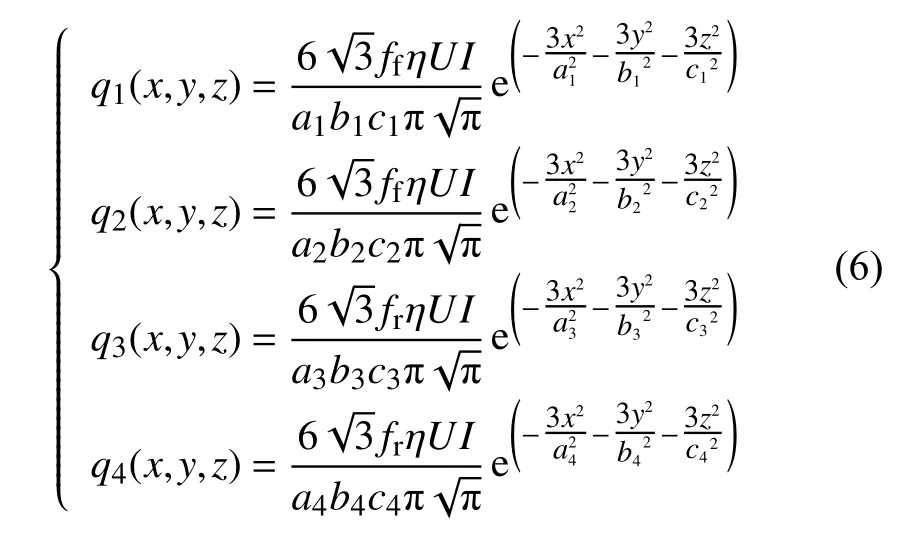
式中：a1，b1，c1和a2，b2，c2分别为四椭球热源模型前1/8 椭球20 钢侧和铝青铜侧的热源熔池形状参数；a3，b3，c3和a4，b4，c4分别为四椭球热源模型后1/8 椭球20 钢侧和铝青铜侧的热源熔池形状参数，如图9 所示.图9b 为图9a 中熔池的局部放大图.经过校核，四椭球热源形状参数如表4 所示.

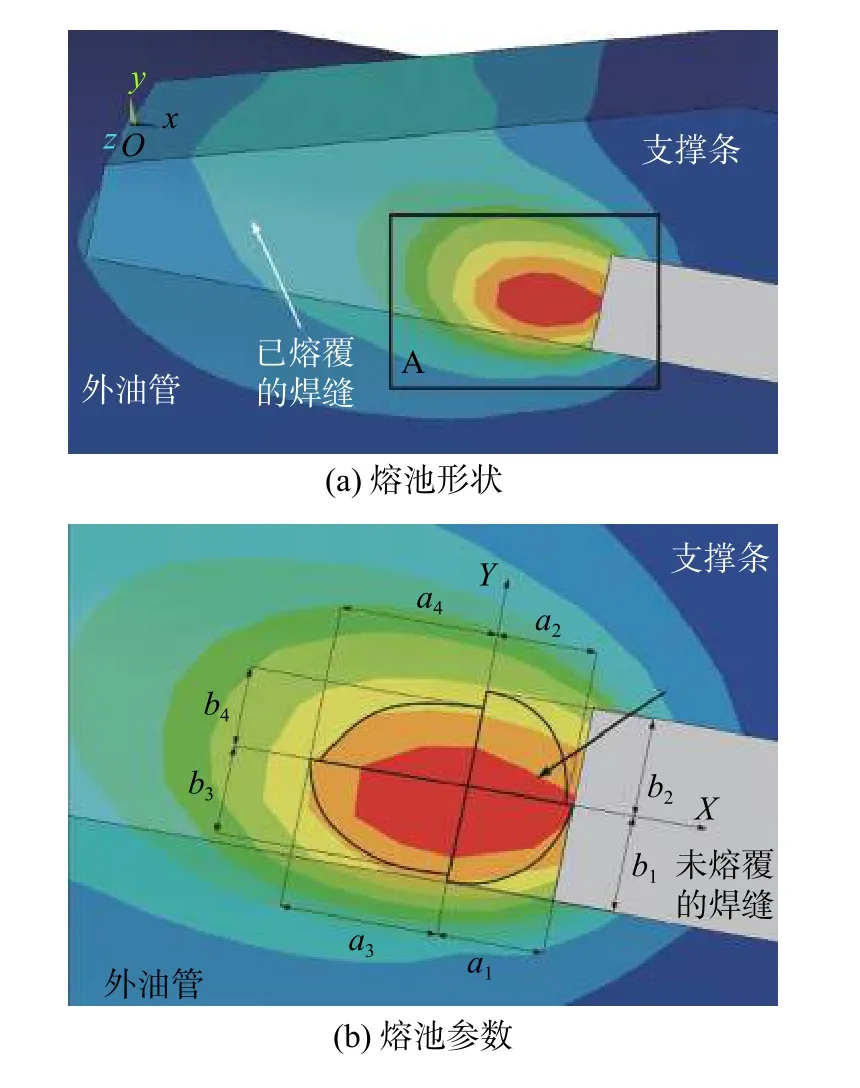
图9 四椭球热源参数Fig.9 Parameters of quadra ellipsoid heat source.(a)shape of molten pool;(b) parameters of molten pool

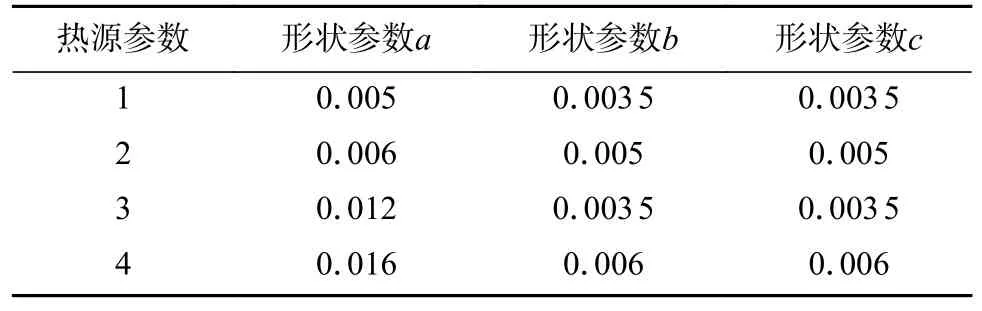
表4 四椭球热源参数值(m)Table 4 Values of heat source parameters

对于长焊缝1st，2nd，使用四椭球热源模型就可以来描述焊接热量的分布.对于焊缝3、焊缝4，采用均匀体热源来描述其焊接能量的分布，其热源表达式如式(7)所示.

式中：V为热源作用的体积，m3.

焊接过程中，散热的边界条件主要包括对流和辐射，焊接过程中损失的总热量Qloss可以表示为

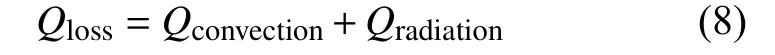
式中：Qconvection为对流散热量，J；Qradiation为辐射散热量，J.

在有限元计算中将焊接过程中对流散热系数h和辐射散热系数综合成总散热系数htotal，由式(9)[27]计算可得.

式中：T为材料表面当前的温度；Tamb为材料的环境温度20 ℃；ε为辐射效率取0.8[28]；σ为斯蒂芬-波尔兹曼常数，5.67 × 10-8W/(m2·K4)；h为材料的对流换热系数，对流换热系数h如图10[17]所示.

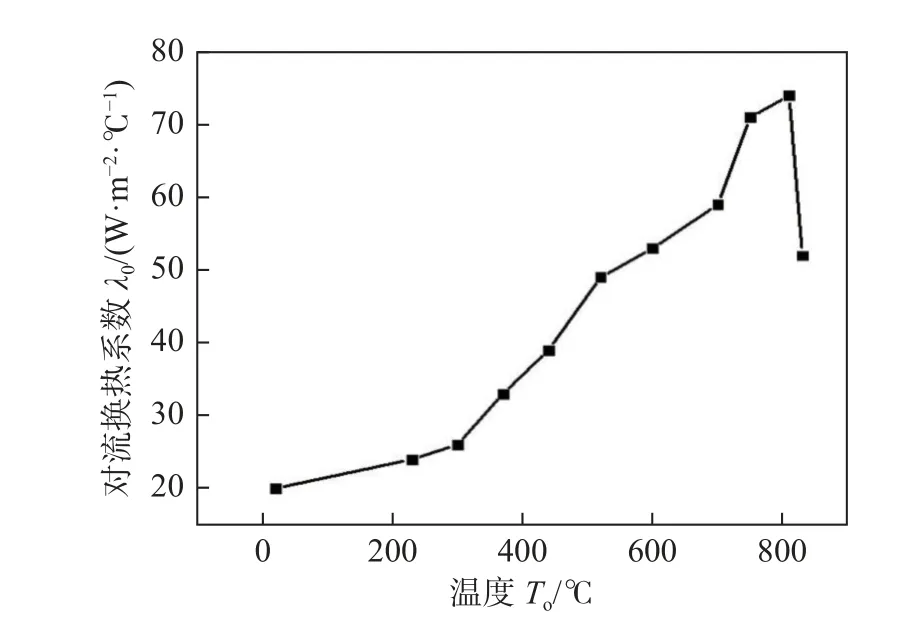
图10 对流换热系数Fig.10 Convective heat transfer coefficient

2.3 应力场计算

焊接过程中，材料会发生弹性应变、塑性应变、热应变、相变应变和蠕变应变.对于低碳钢、铝青铜，相变应变对于总应变的影响不明显.同时，焊接时焊件的高温停留时间短，可以忽略蠕变应变的影响[29].因此，总的应变εtotal可以分为以下3 个部分[18].

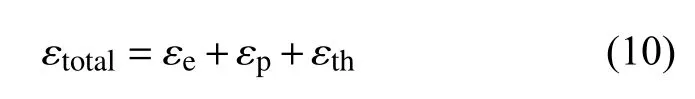
式中：εe,εp,εth分别为弹性应变、塑性应变、热应变.

文中在建立材料力学模型的时候将材料熔点的力学性能参数设置的比常温下数值小3 个数量级[30].图11 为20 钢和QAl9-4 铝青铜的力学性能参数.对于材料的塑性应变，用双线性随动强化(bilinear kinematic,BKIN)曲线来描述材料产生塑性应变后应力与应变之间的关系.20 钢和铝青铜的双线性随动曲线如图11c 和图11d 所示[17-19]，切线模量取为弹性模量的1/20[31].

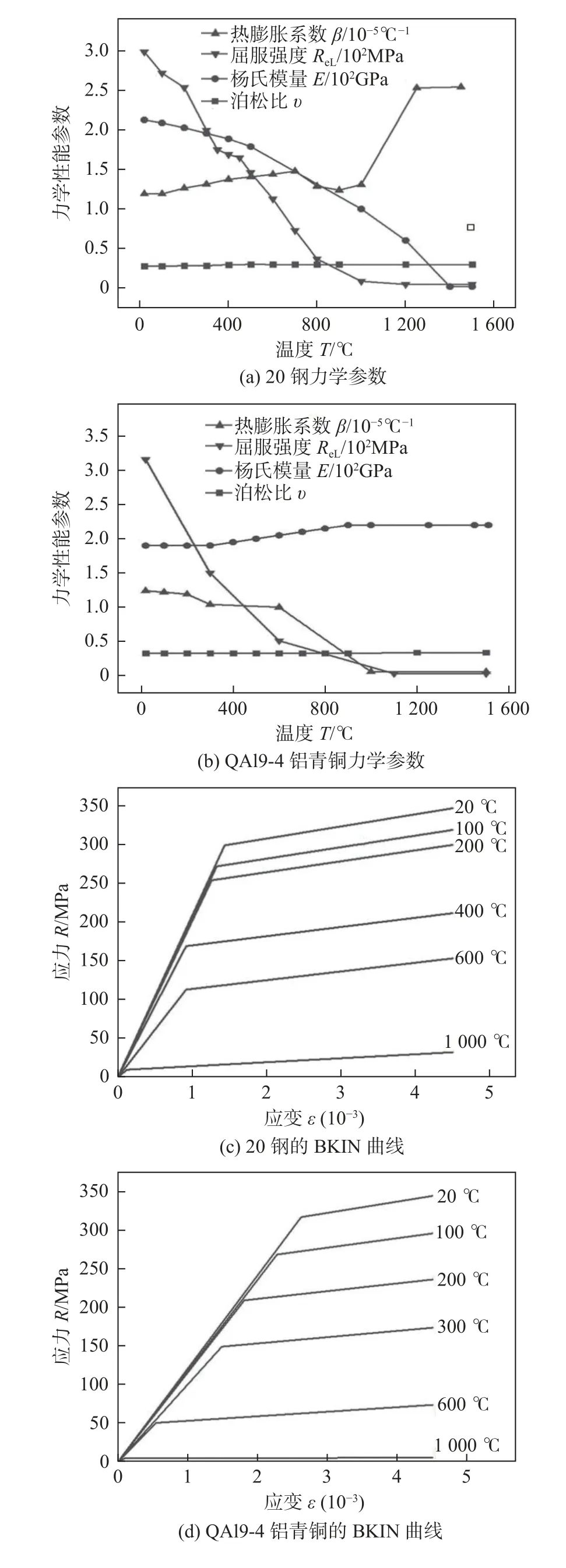
图11 力学参数Fig.11 Thermal mechanical properties.(a) mechanical parameters 20 steel;(b) mechanical parameters of QAl9-4 aluminum bronze;(c) BKIN curve of 20 steel;(d) BKIN curve of QAl9-4 aluminum bronze

应力场计算的约束条件如图6 所示，对左侧端面4 个节点添加x，y，z方向的位移约束，对右侧4 个节点添加y，z方向的位移约束.

3 结果与讨论

3.1 温度场计算结果

焊接热影响区可以分为粗晶区、细晶区和部分转换区(partially transformed region，PTR)3 个区域.通常使用奥氏体转变的起始温度Ac1来代表PTR和母材相变区域的温度分界线即735 ℃作为PTR的终止线，焊接熔合线(fusion line，FL)的温度为铝青铜熔点的温度1 037 ℃.

图12 为长焊缝和短焊缝的热影响区.如图12a所示，将有限元计算得到的长焊缝熔池形状与试验测量的长焊缝熔池形状进行对比，可以看出铝青铜的熔合线FL、20 钢焊接热影响区的终止线PTR 均与有限元的计算结果吻合良好.如图12b 所示，截取油管端部的有限计算温度场结果与试验获得的温度场结果进行对比，可以看出油管端部20 钢的PTR 与试验获得PTR 吻合良好，QAL9-4 铝青铜熔合线FL 吻合的效果也良好，但是存在着一些误差.造成这种误差的主要原因是端部的焊缝由手工沿着油管外径弧面焊接完成，焊接难度较高，焊缝形貌控制困难.有限元建立时忽略了这部分手工焊接因素的影响，所以与试验测量结果之间存在一定的误差，整体吻合比较良好.

图12 长、短焊缝的热影响区对比Fig.12 Comparison of HAZ of long bead and short bead.(a) long bead;(b) short bead

3.2 应力场计算结果

图13 为油管的轴向残余应力云图和定义路径L1，L2.从图13a 可以看出，油管在支撑条的两侧呈现出“拉-压-拉”的应力状态.油管在支撑条端部及其两侧的轴向残余应力比较大，是焊接接头质量分析的重点位置.

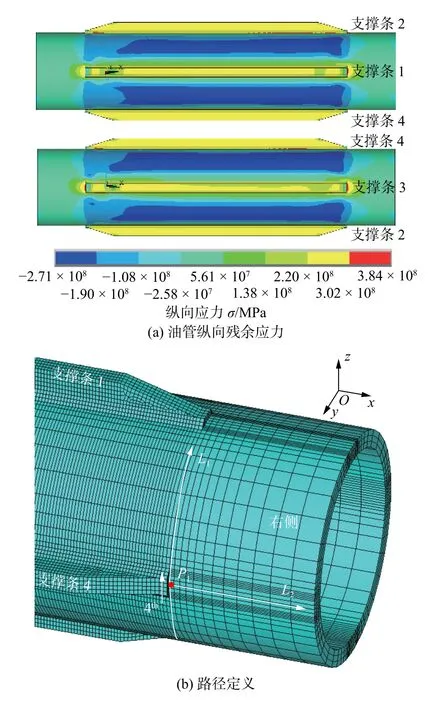
图13 油管纵向残余应力及路径定义Fig.13 Longitudinal residual stress of pipe and definition of paths.(a) longitudinal residual stress of oil pipe;(b) definition of path

图14 为油管有限元计算的残余应力与试验中残余应力的对比.定量比较沿着L1方向上有限元计算结果与试验测试结果，如图14a 和图14b 所示.无论是在数值上还是趋势上，沿着路径L1有限元计算的轴向残余应力与周向残余应力的结果与试验结果都基本一致.比较了支撑条4 右侧的沿着路径L2的有限元计算结果与试验测量的残余应力结果，如图14c 和图14d 所示.无论是轴向残余应力还是周向残余应力有限元的计算结果与试验结果在分布趋势基本一致.

图14 模拟与试验结果中残余应力对比Fig.14 Comparison of residual stresses between simulation and test results.(a) longitudinal residual stresses of points 1-6;(b) transverse residual stress of points 1-6;(c) longitudinal residual stresses of points 7-9;(d) transverse residual stress of points 7-9

4 焊接工艺

4.1 长焊缝简化

虽然文中已考虑到通过划分渐变网格的方式来降低网格的数量，但油管模型较大，最终计算时间还是很长.试验室的工作站配置为：处理器型号i9-10900F，内存128 G，内存频率2 933 MHz.油管的热力耦合计算共计耗时58.5 h.结果发现在焊接进行到第8 s 时，焊接温度场已进入稳定状态，热源中心的最高温度维持在1 800 ℃左右，焊接热影响区的大小基本保持不变，只有在焊接端部支撑条端部时，温度才会有一些变化.从图14a 可以看出，在支撑条两侧长度方向上较长的一段范围内，不论是数值上还是分布趋势上钢管的残余应力变化都不大，也就是长焊缝1st，2nd的长度对于油管中间部位的残余应力形成影响不大.当计算资源有限时，对油管这种焊缝很长的结构，长焊缝按照实际长度建模，计算效率比较低.因此，将油管长焊缝1st,2nd的总长度减短，建立图15 所示简化的油管几何模型.有限元模型中节点总数为68 601 个，单元数为54 800 个.热力耦合计算时，载荷输入和边界条件均与原模型一致.

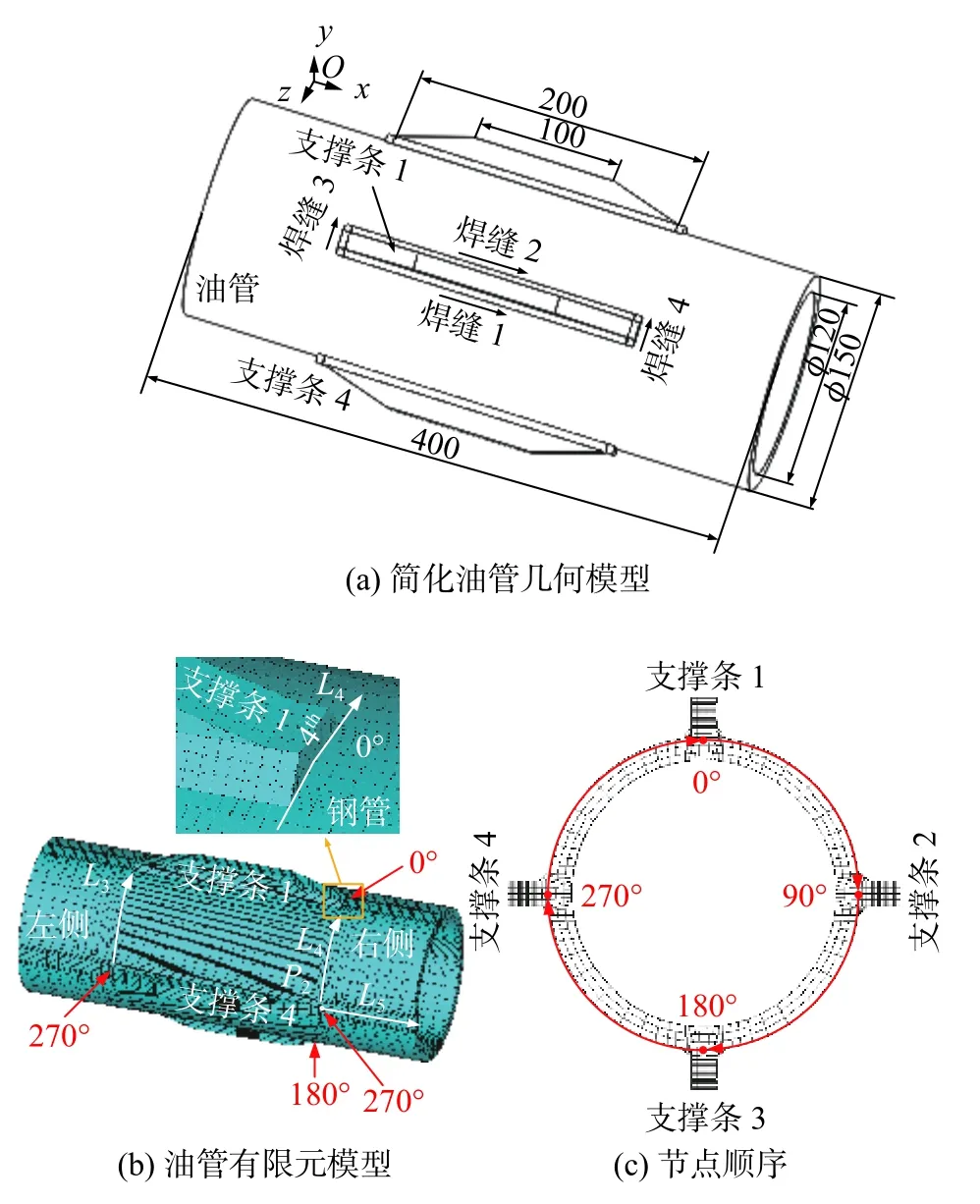
图15 简化模型网格及路径定义Fig.15 Grid of simplified model and definition of paths.(a) geometry of simplified pipe;(b) finite element model of pipe;(c) sequence of node

图16 为简化模型和原模型的von Mises 应力场.从图16 可知，两者在Von Mises 应力的数值和分布趋势上基本一致.

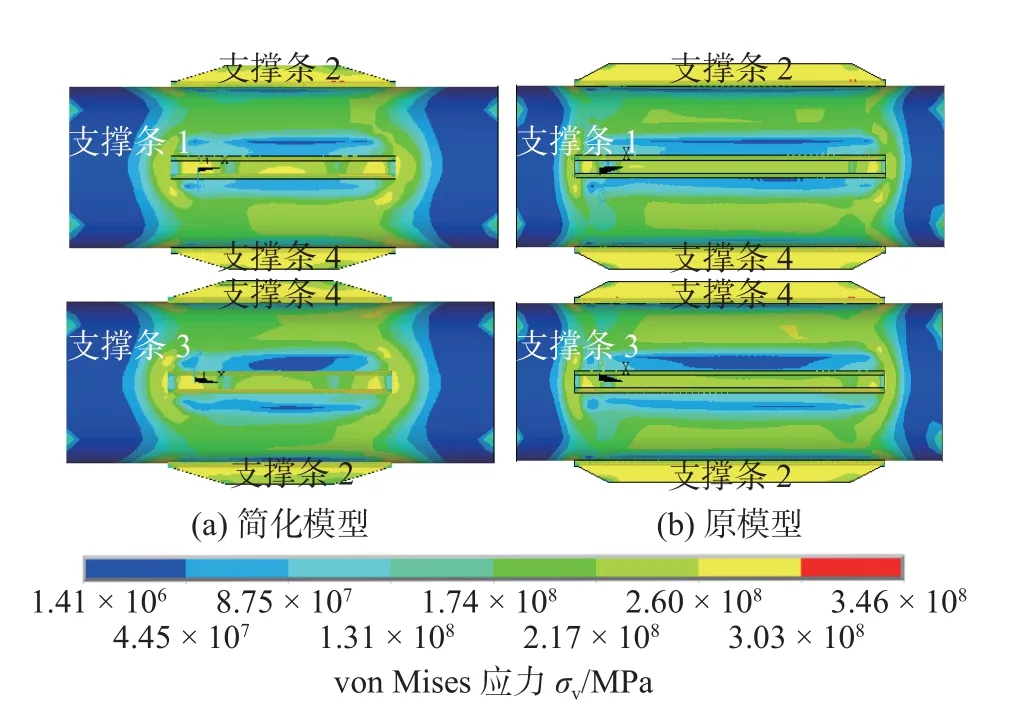
图16 von Mises 应力场Fig.16 von Mises stress

为了进一步验证简化模型计算结果的可靠性，定量对比了原模型和简化后模型的应力场计算结果.首先定义沿着钢管圆周方向上的路径L3和L4，P2为支撑条4的焊缝4th下表面中点.定义沿着钢管轴向方向上的路径L5，其起始点为P2，如图15b所示.在原模型中，路径L3，L4为其在支撑条端部相同的相对位置，按照顺时针方向依次提取了钢管上对应节点的应力值，节点顺序如图15c 所示.图17为沿路径L3和L4轴向与周向残余应力及von Mises 应力的对比.从图17a 和图17b 可知，两个模型的轴向残余应力和周向残余应力在多数节点处几乎是相同的，两者不论是在数值上还是趋势上都具有良好的一致性.从图17c 和图17d 可以看出，原模型和简化模型沿路径L3的von Mises 应力无论是在数值上还是趋势上都具有良好的一致性.在钢管的右侧，沿路径L4的von Mises 应力在分布趋势和大小上都比较吻合.

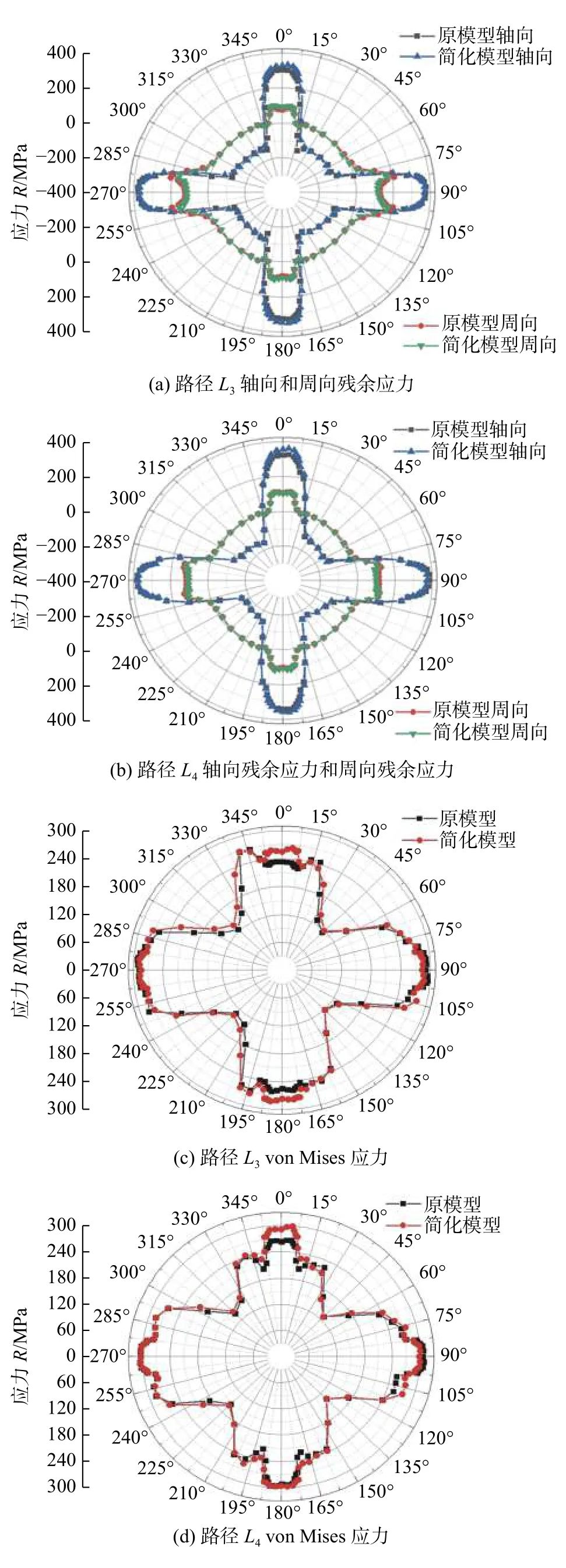
图17 残余应力对比Fig.17 Comparison residual stress.(a) axial and circumferential residual stress along path L3;(b) axial and circumferential residual stress along path L4;(c) von Mises stress along path L3;(d) von Mises stress along path L4

图18 为钢管的von Mises 应力误差及油管端部残余应力对比.钢管的von Mises 应力沿路径L3的最大误差为14.1%，其中91.6%的节点误差都在10%以内，61.4%节点的误差在5%以内.钢管沿路径L4的von Mises 应力最大误差为11.23%，其中95.8%的节点误差都在10%以内，69.7%的节点误差在5%以内.从图18b 和图18c 可以看出，原模型和简化模型的轴向应力、周向应力、von Mises 应力曲线都吻合良好.轴向应力的最大误差为3.46%；周向应力的最大误差为11.9%，91.6%的误差都在10%以内；von Mises 应力最大误差为5.56%.

图18 Von Mises 应力误差及油管端部残余应力对比Fig.18 Von Mises stress error and residual stress comparison at end of pipe.(a) von Mises stress error;(b) axial and circumferential stress along path L5;(c) stress along path L5 von Mises

无论是在支撑条的两侧还是在支撑条的端部，简化后的模型与未简化模型在von Mises 应力的大小和分布趋势上都具有良好的一致性，验证了文中简化模型的有限元计算的有效性.简化后的有限元模型温度场和应力场的耦合计算共计耗时6.9 h，计算速度为未简化模型的8.5 倍.

4.2 结构对称性的影响

建立只焊接一根支撑条的油管有限元模型，如图19 所示.文中后续将只焊接了单根支撑条油管模型称为结构1，如图19a 所示.除了支撑条的个数不同外，结构1 的几何模型参数均与简化模型几何参数相同.网格划分结果如图19b 所示，网格节点数为34 371 个，单元数为26 552 个.热力耦合计算的载荷输入与边界条件、单元类型等均与简化模型相同.

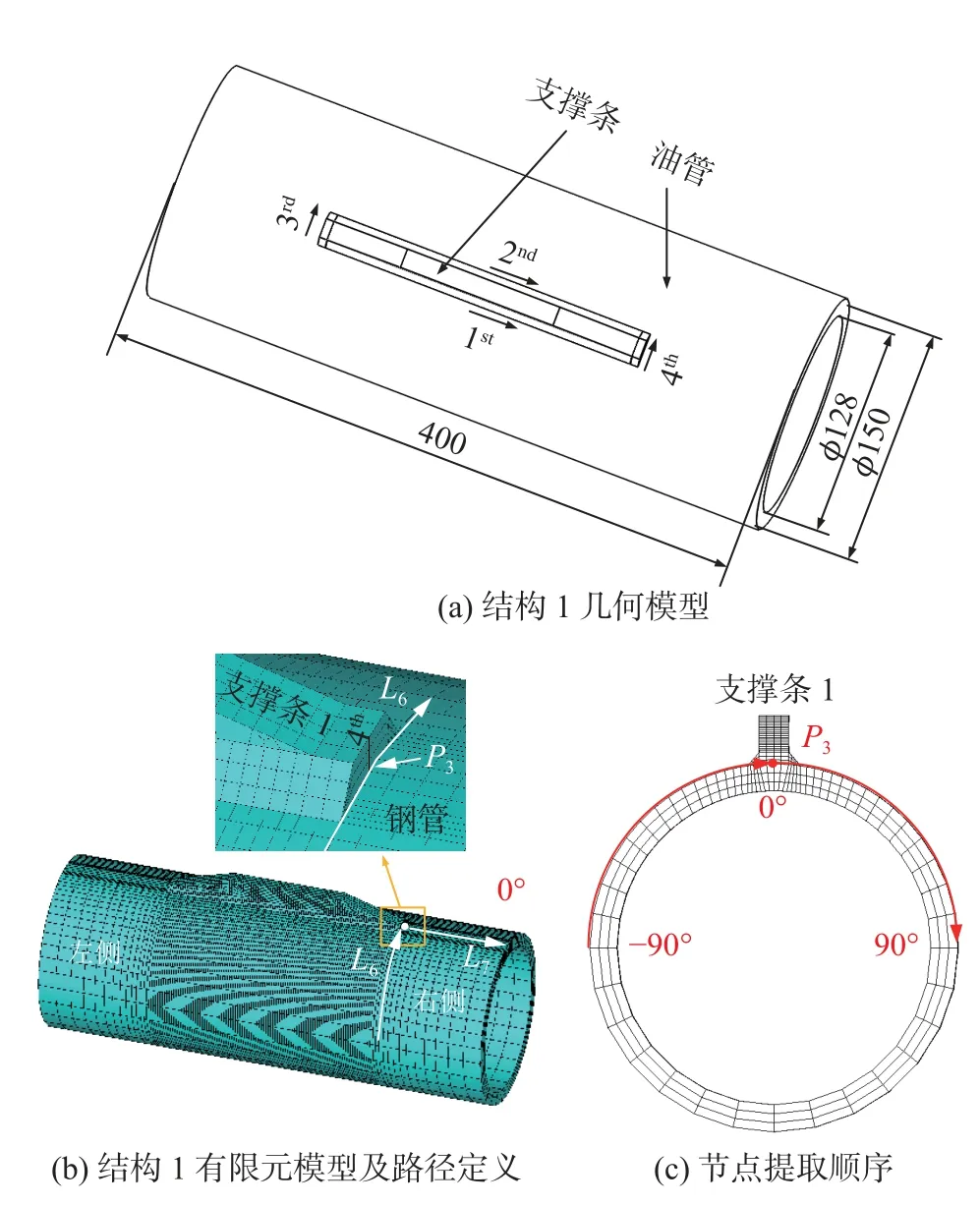
图19 结构1 有限元模型Fig.19 Finite element model of structure1.(a) geometric model of structure 1;(b) finite element model and path definition of structure1;(c)sequence of nod

图20 为结构1 的von Mises 应力场.从图20可以看出，结构1 支撑条的端部和两侧von Mises应力在数值和范围上均大于简化模型支撑条1 位置的残余应力.出现这种现象的原因是结构1 只焊接一根支撑条，整个油管的对称性较差，油管的热变形不对称，所以残余应力更大.相比之下，焊接4 根支撑条的模型结构对称性较好，在各个位置上热变形与热膨胀比较均匀，因此最终总体的残余应力在数值和范围上也更小.

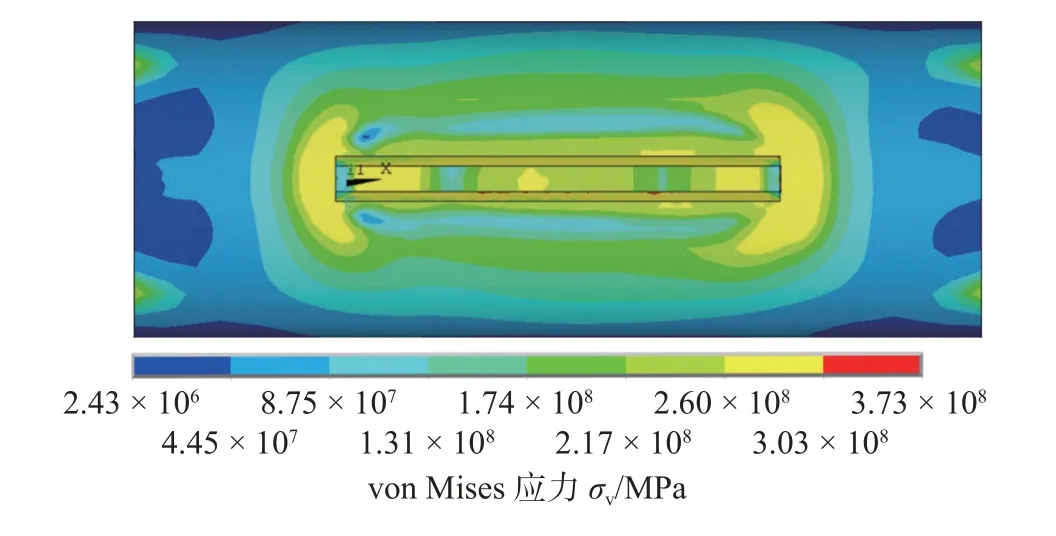
图20 结构1 的von Mises 应力场Fig.20 Von Mises stress field of structure 1

在结构1 中，定义了路径L6，P3为L6的中点，也就是支撑条1 焊缝4 下表面的中点，路径L7的起始点为P3，如图19b 所示.在简化模型中，L6为支撑条1 右侧端部相对应位置的路径.定量对比结构1 和简化模型沿着L6的残余应力，如图21 所示.从图21a 可知，在-45°～ 45°的范围内两者轴向残余应力的趋势是一致的，但单根支撑条油管模型沿L6的轴向残余应力大于简化模型.在图21b 的von Mises 应力对比中，这种现象更加明显，出现这种现象的原因是单根支撑条油管模型的结构对称性比较差，结构变形不对称导致最终形成的残余应力数值比较大.在-90°～-45°和45°～ 90°范围内，随着距离支撑条1 越来越远，单根支撑条模型的轴向应力始终为压应力，但是简化模型的轴向应力逐渐由压应力变为拉应力.出现这种现象的原因是简化模型钢管的轴向残余应力受到4 根支撑条的共同影响，随着距离支撑条1 增加，钢管的轴向残余应力受支撑条2 和支撑条4 的影响越大，因此轴向残余应力逐渐由压应力变为拉应力.在周向应力上两者呈现的也是相同的规律，不过在角度范围和数值上存在着的区别，这与钢管在不同的方向上热变形能力有关.

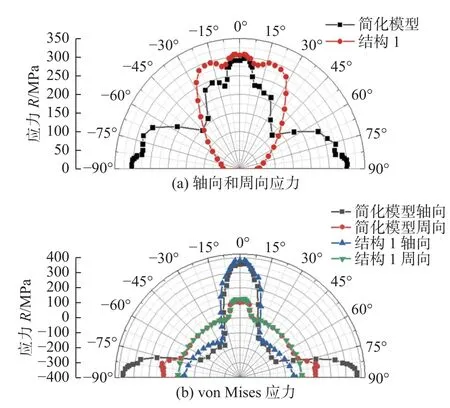
图21 路径L6 残余应力对比Fig.21 Comparison of stress on path L6.(a) axial and circumferential stress;(b) von Mises stress

图22 为简化模型路径定义及残余应力.如图22a 所示，在简化模型中定义了沿着油管圆周方向上的路径L8，P4为路径L8的中点，定义路径L9的起始点为P4.定量对比了简化模型沿路L9的von Mises 应力与结构1 中沿路径L7的von Mises应力，如图22b 所示，两者都具有良好的一致性，结构1 支撑条1 端部的von Mises 应力大于支撑条4 的von Mises 应力.定量对比简化模型沿路径L8与结构1 沿路径L6的残余应力，如图23 所示.从图23a 可以看出，在-30°～ 30°的范围内，支撑条4 的轴残余应力与支撑条1 的残余应力一致性良好，角度在-75°～ 75°的范围内，两者的周向残余应力呈现出了良好的一致性.从图23b 可以看出，在-45°～ 45°范围内两者的von Mises 曲线也呈现了良好的一致性.

图22 简化模型路径定义及残余应力Fig.22 Simplified model path definition and comparison of residual stress.(a) definition of path;(b) sequence of nod;(c) residual stress

图23 最薄弱位置处的残余应力对比Fig.23 Residual stress comparison at weakest location.(a) residual stress on both sides of support;(b)von Mises stress on both sides of support

在-30°～ 30°的角度范围内，结构1 支撑条1 周围的钢管能够很好的反应简化模型支撑条4 在对应角度范围内钢管的残余应力分布.结构1 能够反映出油管最薄弱位置处的残余应力分布，可以使用只焊接了一个支撑条的油管模型来代替简化模型来研究油管最薄弱位置处的残余应力.单根支撑条模型的计算速度是简化模型的2.9 倍，是原模型的24.3 倍.