考虑用户分布情况的中压架空单辐射线路最优分段数计算
2022-05-25曹华珍李浩吴亚雄高崇王梓珺王承民
曹华珍 李浩 吴亚雄 高崇 王梓珺 王承民







摘要:分段是影响中压架空线路可靠性水平的重要因素,如何确定中压架空线路的最优分段数是配电网规划的难点之一。不同于以往分析可靠性时通常假定用户均匀分布,进一步分析讨论了用户分布不均对中压架空单辐射线路可靠性水平和最优分段数的影响。首先建立了不同用户分布情况的数学模型,然后基于解析法推导出不同用户分布情况下的可靠性指标以及最优分段数的量化计算公式,并进一步综合考虑经济性和可靠性提出了考虑用户分布情况的最优分段数的表达式。仿真算例验证了理论推导的正确性。
关键词:用户分布;供电可靠性;架空单辐射;最优分段数
DOI:10.15938/j.jhust.2022.02.015
中图分类号: TM715
文献标志码: A
文章编号: 1007-2683(2022)02-0114-00
Calculation of Optimal Segment Number of MV Overhead
Single Radial Line Considering User Distribution
CAO Hua-zhen LI Hao WU Ya-xiong GAO Chong WANG Zi-jun WANG Cheng-min
(1.Power Grid Planning Center of Guangdong Power Grid Company,Guangzhou 510080,China;
2.School of Electronic Information and Electrical Engineering, Shanghai Jiaotong University, Shanghai 200240, China)
Abstract:Segmentation is an important factor affecting the reliability level of medium voltage overhead lines. How to determine the optimal number of segments of medium voltage overhead lines is one of the difficulties in distribution network planning. Different from the assumption that users are evenly distributed in the past reliability analysis, this paper further analyzes and discusses the influence of uneven distribution of users on the reliability level and optimal number of sections of medium voltage overhead single radial lines. Firstly, the mathematical model of different user distribution is established, and then the quantitative calculation formula of reliability index and optimal number of segments under different user distribution is derived based on analytical method. Furthermore, the expression of optimal number of segments considering user distribution is proposed considering economy and reliability. The simulation example verifies the correctness of the theoretical derivation.
Keywords:user distribution; reliability of power supply; overhead single radial line; optimal number of segments
0引言
配電网连接到用户,与用户的安全、用电的可靠有直接的关系[1-2]。因此,合理规划配电网对于提高电力系统可靠性以及保证电网的经济运行有重大的意义[3]。其中网架结构作为配电网可靠性规划的基石,在一定程度上左右了供电可靠性的提升空间[4-5]。而馈线分段作为网架结构的一大特征,在隔离故障、减少停电时间方面起着至关重要的作用[6-7]。
国外对于馈线分段的已有研究采用蚁群优化算法求解分段开关的最优配置方法[8]。在国内的相关研究中,文[9]研究了各种典型接线模式下供电能力的变化机理。文[10]结合经济性与可靠性,考虑采用断路器分段开关和负荷开关2种情况,提出了一种高可靠性分段原则和小分段的接线模式。文[11]建立了中压配电网多分段多联络接线的一般模型,分析了分段和联络对可靠性的影响规律,综合考虑年停电损失费用和电网投资年值,给出了不同边界条件下可行的多分段多联络配置方案。文[12]定义了开关位置灵敏度最大的单开关定位通用指标,并据此提出了中压架空线开关配置三阶段优化算法。文[13-14]分别采用小生境遗传算法和免疫算法对分段开关的配置问题进行求解。通过CPLEX求解混合整数线性规划模型,文[15]研究了利用分段和联络开关的网络优化重构问题。文[16]则研究了考虑分支线路的开关与自动化终端的优化配置。文[17]针对敏感负荷的可靠性需求,通过改进的最小割集法建立开关的优化配置模型。文[18]基于可靠率指标研究中压馈线的优化分段问题,但得到的结果是架空线的最小分段数。
以上文献所提计算模型较为复杂,并大多采用智能算法对配电网的分段配置进行求解,但通过仿真计算得到的结果往往不具有一般性。为解决此问题,文[19]根据配电网规划分段指导原则,通过推导得出了不同典型接线模式下的最优分段数的通用表达式。文[20]采用故障模式后果分析法,推导出架空线路多分段多联络接线模式下,其供电可靠性指标对应的最优分段数。以上二者虽然能从理论的角度上指导馈线进行分段,但在进行理论分析时,均采用了用户均匀分布的假设条件,没有考虑用户不均匀分布带来的影响。而本文将在这两篇文献的基础上更进一步,研究用户分布不均匀时对线路可靠性和最优分段数的影响。首先根据用户分布均匀程度这一概念,对用户分布形式进行划分,并提出具体的表达式;其次,以架空单辐射接线形式为研究对象,定量分析分布均匀程度对可靠性的影响,建立各用户分布下可靠性指标的计算公式;然后,根据考虑分布均匀程度的可靠性指标,得出综合考虑可靠性与经济性的最优分段数;最后,通过算例分析,对所提方法进行验证。
1用户分布情况的数学模型
在以往研究中,往往假定线路上的用户为均匀分布。但实际电网中,用户往往是分布不均的,这也导致理论分析的结果与实际情况之间存在一定偏差。因此,定义如下用户分布均匀程度公式:
式中:α为分段k的用户分布均匀程度;N为分段数;C为分段k的用户数;C为总用户数。
显然,当α=1时表明分段k的用户分布为平均水平,当α>1时表明分段k的用户分布大于平均水平,当α<1时表明分段k的用户分布低于平均水平。
1)头重脚轻。
是首端用户较多而末端用户较少的分布方式,其用户分布均匀程度可设为
式中:β为用户分布均匀程度随分段k变化的斜率,且β>0;α为初始值,亦为末端分段的用户数,且易知0<α<1。
由用户均匀分布程度的定义,可知此种分布情况下的用户总数与平均分布情况下的用户总数相等,即
2用户分布与可靠性的量化分析
2.1假设条件
为了方便计算和讨论,做出以下假设和简化:
1)仅考虑单点故障,不考虑多重故障,也不考虑计划停电影响。
2)不考虑上级电网的影响以及与开关紧邻的两侧隔离开关故障的影响。
3)不考虑负荷水平与转供容量的影响,即只要认为在同一电压等级拓扑上该用户与联络开关有电气连接,则该用户负荷可转供。
4)不考虑熔断器的故障,且由于配变故障时其上方的熔断器会可靠開断,从而将故障限定在用户接入点,因此为了简化也暂不考虑配变故障。
5)设中压配电网的馈线总共有N段,总用户数为C,总长度为L。并假设馈线均匀分段(即每段长度为L/N)。
2.2理论推导
2.3延伸讨论
3考虑用户分布的中压架空线最优分段数
3.1基于可靠性的最优分段数
3.2综合考虑可靠性和经济性的最优分段
在配电网规划阶段,除了考虑可靠性提升效果外,还需要考虑实施成本,因此通过成本折算,得出综合考虑经济性和可靠性的最优分段策略。将总费用描述为分段开关费用和停电损失费用之和。总费用函数可以表示为
4算例分析
选取某配电网的5条中压架空线单辐射线路,设备故障参数如表2所示,平均故障隔离转供时间取0.5h;假设该线路分别服从不同的用户分布情况,并设α=0.5;5条线路的具体参数及不同用户分布下的可靠性计算结果如表3所示。
由表3可以看出,这5条线路在不同用户分布下的SAIDI-F值均满足如下规律:头重脚轻时最小,头轻脚重时最大,均匀分布、纺锤形和沙漏形居中。
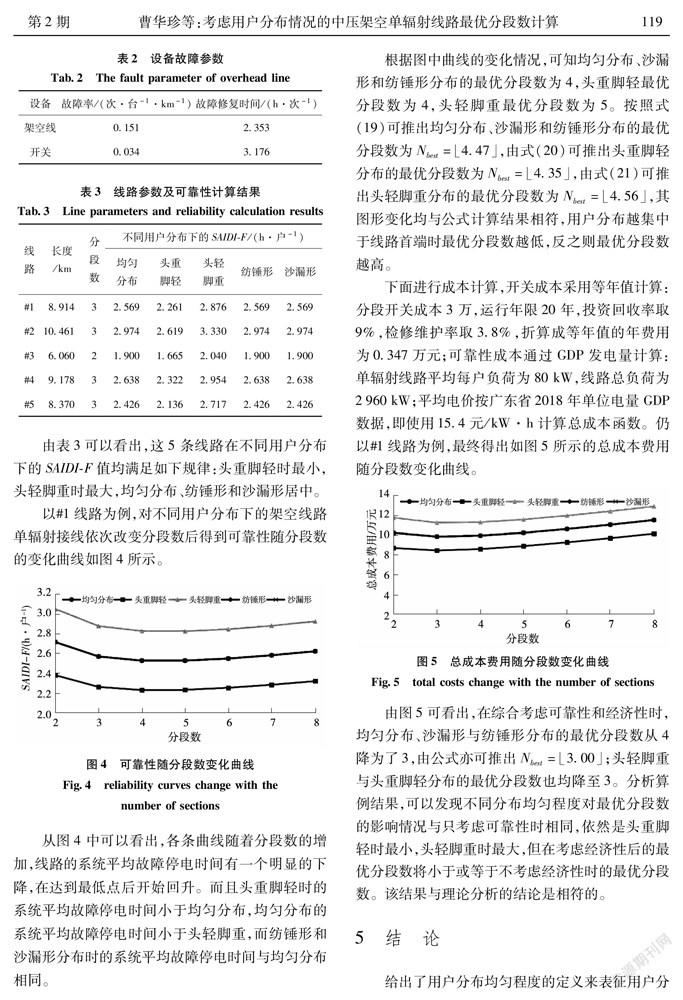
以#1线路为例,对不同用户分布下的架空线路单辐射接线依次改变分段数后得到可靠性随分段数的变化曲线如图4所示。
从图4中可以看出,各条曲线随着分段数的增加,线路的系统平均故障停电时间有一个明显的下降,在达到最低点后开始回升。而且头重脚轻时的系统平均故障停电时间小于均匀分布,均匀分布的系统平均故障停电时间小于头轻脚重,而纺锤形和沙漏形分布时的系统平均故障停电时间与均匀分布相同。
根据图中曲线的变化情况,可知均匀分布、沙漏形和纺锤形分布的最优分段数为4,头重脚轻最优分段数为4,头轻脚重最优分段数为5。按照式(19)可推出均匀分布、沙漏形和纺锤形分布的最优分段数为N=4.47,由式(20)可推出头重脚轻分布的最优分段数为N=4.35,由式(21)可推出头轻脚重分布的最优分段数为N=4.56,其图形变化均与公式计算结果相符,用户分布越集中于线路首端时最优分段数越低,反之则最优分段数越高。
下面进行成本计算,开关成本采用等年值计算:分段开关成本3万,运行年限20年,投资回收率取9%,检修维护率取3.8%,折算成等年值的年费用为0.347万元;可靠性成本通过GDP发电量计算:单辐射线路平均每户负荷为80kW,线路总负荷为2960kW;平均电价按广东省2018年单位电量GDP数据,即使用15.4元/kW·h计算总成本函数。仍以#1线路为例,最终得出如图5所示的总成本费用随分段数变化曲线。
由图5可看出,在综合考虑可靠性和经济性时,均匀分布、沙漏形与纺锤形分布的最优分段数从4降为了3,由公式亦可推出N=3.00;头轻脚重与头重脚轻分布的最优分段数也均降至3。分析算例结果,可以发现不同分布均匀程度对最优分段数的影响情况与只考虑可靠性时相同,依然是头重脚轻时最小,头轻脚重时最大,但在考虑经济性后的最优分段数将小于或等于不考虑经济性时的最优分段数。该结果与理论分析的结论是相符的。
5结论
给出了用户分布均匀程度的定义来表征用户分布的特性,并重点分析了头重脚轻、头轻脚重、纺锤形和沙漏形4种典型的用户非均匀分布情况。通过理论推导分析了不同用户分布情况对可靠性指标的影响,并进一步推导了不同用户分布情况下的最优分段数的理论计算公式,最终的算例也验证了理论推导的正确性。得出了不同用户分布情况对中压架空单辐射线路的影响的主要结论。
1)用户分布越集中于线路首端,则可靠性水平越高,最优分段数也越低;越集中于线路末端,则可靠性水平越低,最优分段数也越高。具体到4种典型的用户分布不均情况,则有头重脚轻分布时的可靠性水平最高、最优分段数最低,头轻脚重分布时的可靠性水平最低、最优分段数最高,纺锤形和沙漏形与均匀分布时的可靠性水平和最优分段数均相等。
2)配置分段时对于用户分布密度较低的分段可增加分段线路长度,对于用户分布密度较大的分段宜减少分段线路长度。
3)综合考虑经济性后的最优分段数要低于仅考虑可靠性的最优分段数。
由于篇幅所限,只详细推导了不同用户分布下架空线单辐射接线模式的最优分段数,对于其余接线模式并未延展讨论,但其推导原理和过程是相同的。本文还存在一些不足,比如未讨论分支线的影响,这些都将在后续进一步研究完善。
参 考 文 献:
[1]郭焱林,刘俊勇,魏震波,等.配电网供电能力研究综述[J].电力自动化设备,2018,38(1):33.GUO Yanlin, LIU Junyong, WEI Zhenbo, et al. Overview of Power Supply Capacity of Distribution Network [J]. Power Automation Equipment, 2018,38(1): 33.
[2]吴亚雄, 高崇, 曹华珍, 等. 配电网全寿命周期可靠性评估和管理问题研究[J]. 电测与仪表, 2020, 57(13):6.WU Yaxiong, GAO Chong, CAO Huazhen, et al. Research on Life-Cycle Reliability Assessment and Management of Distribution Network[J]. Electrical Measurement & Instrumentation, 2020, 57(13):6.
[3]肖白, 郭蓓. 配电网规划研究综述与展望[J]. 电力自动化设备, 2018, 38(12):200.XIAO Bai, GUO Bei. Review and Prospect of Distribution Network Planning[J]. Electric Power Automation Equipment. 2018, 38(12):200.
[4]鐘士元, 熊宁, 张成昊, 等. 配电网网架结构与配电自动化终端协同规划方法[J]. 电力建设, 2020, 41(3):23.ZHONG Shiyuan, XIONG Ning, ZHANG Chenghao, et al. A Collaborative Planning Method for Distribution Network Structure and Distribution Automation Terminal[J]. Electric Power Construction, 2020, 41(3):23.
[5]曹昉, 张姚, 李赛. 基于网架结构相似性和适应性的主动配电网动态重构[J]. 电力系统自动化, 2019, 43(16):78.CAO Fang, ZHANG Yao, LI Sai. Dynamic Reconfiguration of Active Distribution Network Dynamic Reconfiguration of Active Distribution Network[J]. Automation of Electric Power Systems, 2019, 43(16):78.
[6]WANG Longjun, LIN Jian, LIU Guowei,et al. An MIP-Based Model for the Deployment of Fault Indicators and Sectionalizing Switches in Distribution Networks[J]. Electric Power Systems Research, 2020, 179.
[7]陈锐智, 陈浩, 杨少瑜, 等. 配电网开关的最优配置模型[J]. 智慧电力, 2019, 47(7):76.CHEN Ruizhi, CHEN Hao, YANG Shaoyu, et al. Optimal Configuration Model of Distribution System Switch[J]. Smart Power, 2019, 47(7):76.
[8]ZHANG B Y, PETER C.Reliability Improvement Using Ant Colony Optimization Applied to Placement of Sectionalizing switches[J]. Energy Procedia, 2017, 142.
[9]肖峻,佘步鑫,周欢, 等.配电网供电能力曲线的规律与机理[J].中国电机工程学报,2019,39(16):4732.XIAO Jun, SHE Buxin, ZHOU Huan,et al. Law and Mechanism of Power Supply Capacity Curve of Distribution Network [J]. Chinese Journal of Electrical Engineering, 2019,39(16): 4732.
[10]冯霜, 王主丁, 周建其, 等. 基于小分段的中压架空线接线模式分析[J]. 电力系统自动化, 2013, 37(4):62.FENG Shuang, WANG Zhuding, ZHOU Jianqi, et al. Analysis of Medium Voltage Overhead Line Connection Mode Based on Small Section[J]. Automation of Electric Power Systems, 2013, 37(4):62.
[11]王哲, 罗凤章, 竺笠, 等. 中压配电网接線模式分段和联络优化配置方法[J]. 电力系统及其自动化学报, 2015, 27(S1):83.WANG Zhe, LUO Fengzhang, ZHU Li, et al. Optimization of Sectional and Tie Switches for Medium Voltage Distribution System[J]. Proceedings of the CSU-EPSA, 2015, 27(S1):83.
[12]廖一茜, 张静, 王主丁, 等. 中压架空线开关配置三阶段优化算法[J]. 电网技术, 2018, 42(10):3413.LIAO Yiqian, ZHANG Jing, WANG Zhuding, et al. Three-stage Optimization Algorithm for the Sectionalizing Switch Placement of a Medium Voltage Overhead Line[J]. Power System Technology, 2018, 42(10):3413.
[13]王艳松, 陈国明, 张加胜, 等. 基于小生境遗传算法的配电网开关优化配置[J]. 电工技术学报, 2006(5):82.WANG YanSong, CHEN Guoming, ZHANG Jiasheng, et al. Optimal Switching Device Placement Based on Niche Genetic Algorithm in Distribution Networks[J]. Transactions of China Electrotechnical Society, 2006(5):82.
[14]谢开贵, 周家启. 基于免疫算法的配电网开关优化配置模型[J]. 电力系统自动化, 2003(15):35.XIE Kaigui, ZHOU Jiaqi. Model for Optimal Switching Devices Based on Immune Algorithm in Electric Distribution Networks[J]. Automation of Electric Power Systems, 2003(15):35.
[15]周念成,莫复雪,肖舒严, 等. 计及多电压等级配电网拓扑约束的协调转供优化[J].中国电机工程学报,2021,41(9):3106.ZHOU Niancheng, MO Fuxue, XIAO Shuyan, et al. Coordinated Transfer Optimization Considering Topological Constraints of Multi Voltage Distribution Networks [J]. Chinese Journal of Electrical Engineering, 2021,41(9): 3106.
[16]姚琪,薛玉凤,康志, 等.考虑分支线路的配电网分段开关及自动化终端优化配置模型[J].供用电,2021,38(6):61.YAO Qi, XUE Yufeng, KANG Zhi,et al. Optimal Configuration Model of Sectional Switch and Automation Terminal in Distribution Network Considering Branch Lines [J]. Power Supply and Consumption, 2021,38(6): 61.
[17]唐巍,王辰,张璐, 等.考虑敏感负荷需求和直流故障恢复能力的交直流混合配电网开关配置[J].电力自动化设备,2021,41(5):210.TANG Wei, WANG Chen, ZHANG Lu, et al. Switch Configuration of AC / DC Hybrid Distribution Network Considering Sensitive Load Demand and DC Fault Recovery Capability[J]. Power Automation Equipment, 2021,41(5): 210.
[18]彭卉,张静,吴延琳,等.基于可靠率指标的中压架空馈线分段优化[J].电力自动化设备,2017,37(5):184.PENG Hui, ZHANG Jing, WU Yanlin, et al. Sectional Optimization of Medium Voltage Overhead Feeder Based on Reliability Index [J]. Power Automation Equipment, 2017,37(5): 184.
[19]曹华珍, 陈一铭, 吴亚雄, 等. 中压馈线最优分段数的通用量化表达式[J]. 电网技术, 2019, 43(8):2991.CAO Huazhen, CHEN Yiming, WU Yaxiong, et al. General Quantitative Expression of Optimal Segment Number of MV Feeder[J]. Power System Technology, 2019, 43(8):2991.
[20]吴亚雄, 曹华珍, 高崇, 等. 架空线路N分段N联络接线模式最优分段数计算[J]. 智慧电力, 2019, 47(12):98.WU Yaxiong, CAO Huazhen, GAO Chong, et al. Calculation of Optimal Segment Number of N-Segment N-Connection Mode for Overhead Lines[J]. Smart Power, 2019, 47(12):98.
(编辑:温泽宇)
