一种蚁群优化小波包基选择的方法

邹方豪　张涵　孟良　许同乐　苏元浩

摘要：为了研究已有最优基选择算法在微弱故障信号降噪方面效果差以及终端节点不易确定的问题，依据蚁群算法和小波包的相关理论，分析了小波包基选取的影响因素，对选取规则进行了重新定义，并结合蚁群算法的全局优化能力对新定义的终端节点坐标集和分解层数寻优，给出了一种基于蚁群算法的小波包基优选方法。对比传统最优基选择算法，新方法的收敛性能及分布性能加强了12.5%，在轴承的微弱故障信号降噪过程中，经处理后的信号信噪比提高了46.7%，均方根误差降低了20.4%，验证了新方法的有效性和优越性。

关键词：信号降噪;小波包;最优基选择;代价函数;蚁群算法

DOI：10.15938/j.jhust.2022.02.006

中图分类号： TH17

文献标志码： A

文章编号： 1007-2683（2022）02-0048-07

An Ant Colony Optimization to Optimize Selection Method of Wavelet Packet Basis

ZOU Fang-hao，ZHANG Han，MENG Liang，XU Tong-le，SU Yuan-hao

（School of Mechanical Engineering， Shandong University of Technology， Zibo 255049， China）

Abstract：In order to study the poor effect of the existing best basis selection algorithm in reducing the noise of weak fault signals and the difficulty of determining the terminal node， according to the ant colony algorithm and wavelet packet related theories， the factors affecting the selection of the wavelet packet basis are analyzed， and the selection rules are analyzed. After redefining and combining the global optimization ability of ant colony algorithm to optimize the newly defined terminal node coordinate set and decomposition level， a wavelet packet basis optimization method based on ant colony algorithm is given. Compared with the traditional best basis selection algorithm， the convergence performance and distribution performance of the new method are enhanced by 12.5%. In the process of reducing the noise of the weak fault signal of the bearing， the signal-to-noise ratio after processing is increased by 46.7%， and the root mean square error is reduced by 20.4%， verifying the effectiveness and superiority of the new method.

Keywords：signal noise reduction; wavelet packet; best base selection; cost function; ant colony optimization

0引言

在機械故障诊断过程中，对非平稳故障信号局部特征的处理至关重要[1-3]，小波包变换（wavelet packet transform，WPT）是由Wickhauser等在小波变换的基础上提出的，目前多应用在非平稳信号的处理当中，能够有效反映故障信号的局部时频域特征[4-5]。

小波包基的选择是小波包变换中的关键步骤，对WPT性能的影响很大[6]。由于小波包基数量繁多，如何选取小波包基的最佳组合使得小波包变换的性能最理想，成为国内外学者的研究热点。现如今比较成熟的最优基选择算法（best basis selection， BBS）是以熵为代价函数的“自下而上”的二叉树选择方法[7-9]，通过各节点的熵值大小来判断终端节点，简单高效，但随着分解层数的变化，导致其终端节点数不易确定，且对微弱故障信号的降噪性能表现不佳。

针对目前常用BBS算法存在的缺点以及不足之处，本文提出一种以B-M风险函数代替熵作为代价函数，并重新规定了终端节点选择策略的新型最优基选择方法，利用蚁群算法（ant clony optimization， ACO）对优化目标寻优，找到最合适的小波包基。

最后利用反世代距离评价指标（inverted generational distance， IGD）验证了所提方法的综合性能，通过信噪比（signal-noise ratio，SNR）、均方根误差（root mean squared error，RMSE）以及信号的快速傅里叶变换（fast fourier transform，FFT）图像展示了新方法对微弱故障信号降噪的有效性和优越性。

1小波包介绍

小波变换因其在时频域中均能反映信号的局部特征，故被广泛应用于非平稳信号的分解。但小波变换只针对低频信号进行分解，而忽略了高频信号，对信号造成了不良影响，所以小波包分解正是为解决传统小波分解所具有的此类缺点，对信号的高频区域进一步分解，是小波分解的拓展和延伸[10-11]。

小波包变换公式如下所示：

其中：φ（x）、ψ（x）为函数空间L（R）上的尺度函数与小波函数;h、g为滤波器系数。

小波包基是从该小波包中提取的能构成L（R）的规范正交基，小波包基有无数个，所以确定最佳小波包基对WPT有重要意义[12]。

2蚁群算法

蚁群算法是Dorigo模仿自然界中蚁群行为提出的一种随机算法，具有简单、高效、并行性强等特点，目前在智能算法领域运用很广泛[13-15]。ACO的基本流程如下：在t时刻，蚂蚁处于随机结点，随后蚂蚁不断进行节点转移，直到经过的节点数t=t时停止，假设蚂蚁目前处于节点i，则从节点i移动到节点j的概率为P：

3小波包基择优方法

3.1代价函数的选取

由于存在无数种分解小波包的方法，所以就有无数种小波包基可以组成L2（R），由此看来，所谓小波包基择优，指的是在小波包分解层数确定时，凭借某种“择优标准”，根据实际需要，选取一个满足这个标准的最优基。一般来说，通过定义一个代价函数来表征“择优标准”并利用求解代价函数的最小值来寻找最优基是可行的[17]。

3.2小波包基的选择

BBS算法采用一种由二类节点确定一类节点的自下而上的二叉树分解结构，利用代价函数确定节点类型，并设一类节点为二叉树的终端节点，子节点由二类节点确定。按照传统BBS算法，小波包基的选择是基于熵的，当采集到的微弱故障信号中故障信号与噪声信号的不确定性较低时，信号经小波包处理之后的SNR较低，且容易丢失有效信號，并且由于BBS算法中的最末层节点数为2k个，故终端节点数不容易确定。将B-M风险函数替代熵进行小波包基的选取，同时对终端节点的选取做进一步的规定，可有效提高小波包基选取方法的性能和信号的SNR且尽可能多的保留有效信号。

利用B-M风险函数作为代价函数，并利用全分解结构的小波包对其进行训练。因代价函数具有可加性，所以规定：

将一类节点的坐标纳入寻优库中，由于不同的分解层数k会导致一类节点的数量不同，合理的选择分解层数k和终端节点G对小波包基的选取起到至关重要的作用。所以引入蚁群算法，对分解层数k以及终端节点的坐标（k，j）进行寻优。由终端节点和分解层数确定小波包基之后，对信号分解得到对应的小波包系数，将B-M风险函数作为优化目标函数。

由于ACO具有很强的全局搜索能力和良好的搜索并行性，所以很适合处理类似全局优化的问题。蚁群算法优化步骤如下：

Step1：确定变量的寻优区间。

对于一类节点的坐标（k，j）而言，根据规定1）、2）、3）进行确定，寻优限制条件为终端节点坐标集合D内元素个数等于一类节点数。

对于分解层数k，可利用有用信号的最小频率来大致确定其取值范围[19]。

小波分解的尺度与频率的关系可以表示为：f=ff/j，其中f为尺度j对应的伪频率，f为采样频率，f为小波中心频率。

有用信号的频率f应全部包含在伪频率中，即：

并结合实际数据确定分解层数的取值范围。

Step2：初始化蚁群系统。

设定蚁群系统的各个参数：如系数α、β、ρ及常数Q，蚂蚁的数量m，信息素初始值τ，最大迭代次数，根据寻优区间随机确定蚂蚁的初始城市位置r（集合D，分解层数k时的风险函数值）。

Step3：根据式（2）计算蚂蚁从城市i移动到城市j的概率，其中η（i，j）取差值r-r。

Step4：由式（3），式（4），式（5）对信息素浓度进行更新。其中L为目标函数变化量。

Step5：不断进行循环，直到所有蚂蚁收敛同一路径或者迭代次数达到最大为止，输出最佳集合D及最佳分解层数k，并根据式（6）得到最优小波包基。

4实验验证

仿真数据选用6205-RS号轴承内圈故障振动数据，轴承转速为1750r/min，采样频率设为12kHz，选取内圈故障，故障点直径为0.28mm，由参数可计算出内圈故障特征频率f=160Hz。根据式（9）确定k的取值范围为k∈[3，6]，图1为原始信号图，表1为蚁群算法参数设置。

4.12种终端节点选取方法的对比

针对终端节点坐标集合D与分解层数k进行寻优，二者之间存在相互影响，对于这样的多目标优化算法，采用IGD指标来评价算法的综合性能，该指标通过计算算法获取的个体集合到每个在真实Pareto前沿面上的个体之间的最小距离和，来评价算法的收敛性能和分布性能。计算公式如下所示[20]：

式中：d（v，P）是点v到集合P之间的距离，D（P*，P）越小，算法的综合性能越强。

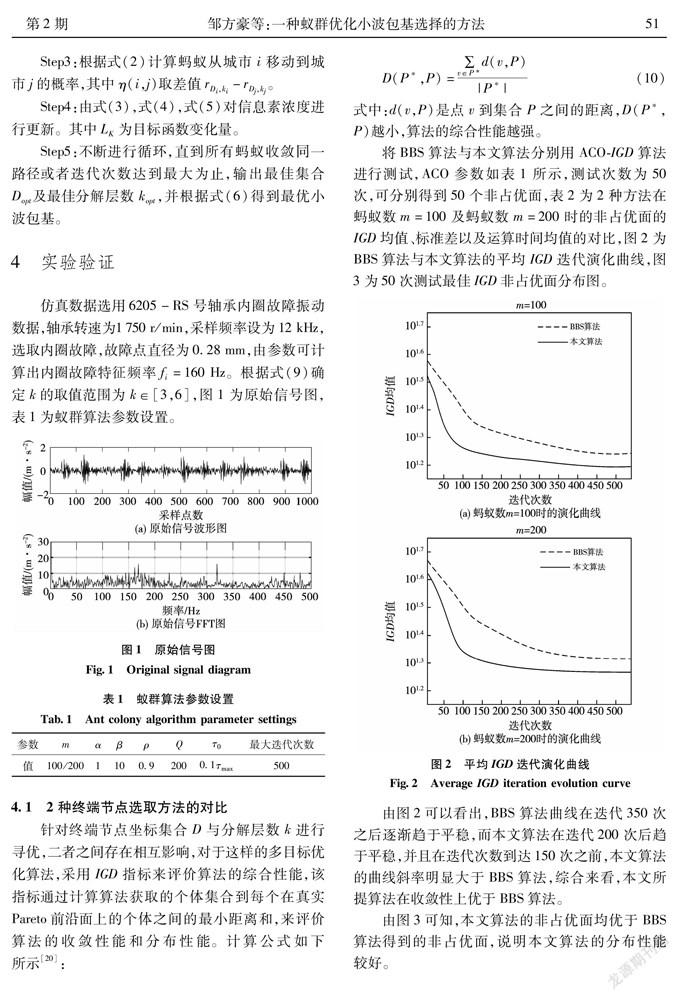
将BBS算法与本文算法分别用ACO-IGD算法進行测试，ACO参数如表1所示，测试次数为50次，可分别得到50个非占优面，表2为2种方法在蚂蚁数m=100及蚂蚁数m=200时的非占优面的IGD均值、标准差以及运算时间均值的对比，图2为BBS算法与本文算法的平均IGD迭代演化曲线，图3为50次测试最佳IGD非占优面分布图。

由图2可以看出，BBS算法曲线在迭代350次之后逐渐趋于平稳，而本文算法在迭代200次后趋于平稳，并且在迭代次数到达150次之前，本文算法的曲线斜率明显大于BBS算法，综合来看，本文所提算法在收敛性上优于BBS算法。

由图3可知，本文算法的非占优面均优于BBS算法得到的非占优面，说明本文算法的分布性能较好。

由表2可以看出，在m=100及m=200时本文算法在非占优面的IGD均值和标准差都小于BBS算法。

综上，本文算法在收敛性与分布性等综合性能上优于BBS算法，通过计算得出，相比于BBS算法改进了12.5%，但在运算时间上BBS算法较快于本文算法，原因主要在于本文算法增加了终端节点的判定步骤。

4.2算法在滚动轴承故障信号降噪方面的性能对比

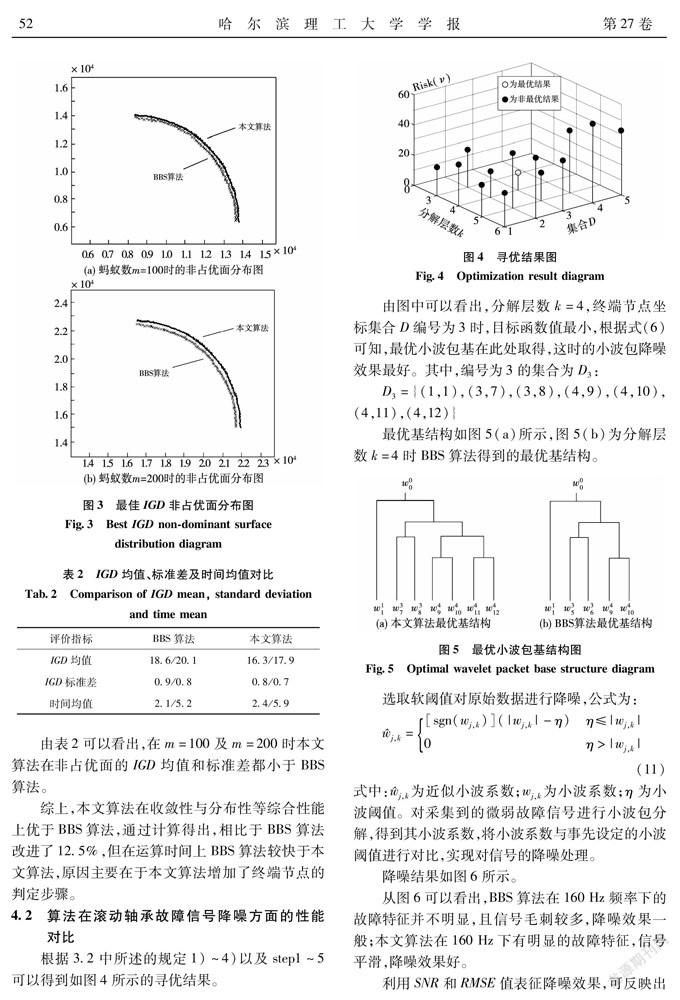
根据3.2中所述的规定1）～4）以及step1～5可以得到如图4所示的寻优结果。

由图中可以看出，分解层数k=4，终端节点坐标集合D编号为3时，目标函数值最小，根据式（6）可知，最优小波包基在此处取得，这时的小波包降噪效果最好。其中，编号为3的集合为D：

最优基结构如图5（a）所示，图5（b）为分解层数k=4时BBS算法得到的最优基结构。

从图6可以看出，BBS算法在160Hz频率下的故障特征并不明显，且信号毛刺较多，降噪效果一般;本文算法在160Hz下有明显的故障特征，信号平滑，降噪效果好。

利用SNR和RMSE值表征降噪效果，可反映出本文方法相比于BBS算法的优势。表3为利用本文方法以及BBS算法进行小波包基择优后的小波包降噪信号SNR和RMSE值对比。其中SNR的计算公式为：

从表3可以看出，本文算法相较于BBS算法，RMSE更低，SNR更高，说明新方法能更好的保留原始信号特征，降噪效果更明显，进而反映出本文方法对于小波包基优选的优越性和有效性。

5结论

BBS算法在处理微弱故障信号时易丢失有效信号，并且随着分解层数的改变，最末端节点数难以确定且终端节点的选取存在随机性。本文针对BBS算法的不足，做了以下改进：

1）利用B-M风险函数作为代价函数进行小波包基的选取，能够在改善SNR与保留原始信号能量之间适当权衡。

2）将分解层数与终端节点的选取相关联，确定优化目标，并提出一种终端节点的选取方法，引入蚁群算法来对优化目标寻优，找出最优分解层数与最优终端节点坐标集合。

通过IGD指标表明本文算法在综合性能上优于BBS算法，通过降噪FFT结果图与SNR、RMSE对比表看出本文算法在降噪性能方面也优于BBS算法，说明本文所提算法是有效的。

参 考 文 献：

[1]XU Tongle， JI Junqing， KONG Xiaojia， et al. Bearing Fault Diagnosis in the Mixed Domain Based on Crossover-Mutation Chaotic Particle Swarm[J]. Complexity， 2021， 2021（6）：1.

[2]时献江，李万涛，高庆康.VMD方法在轴承故障定子电流信号诊断中的应用[J].哈尔滨理工大学学报，2020，25（1）：22.

SHI Xianjiang， LI Wantao， GAO Qingkang. The VMD Method in Diagnosis of Stator Fault and Stator Current Signal[J]. Journal of Harbin University of Science and Technology， 2020， 25（1）： 22.

[3]纪俊卿，张亚靓，孟祥川，等.自适应小波阈值滚动轴承故障振动信号降噪方法[J].哈尔滨理工大学学报，2021，26（2）：124.

JI Junqing， ZHANG Yajing， MENG Xiangchuan， et al. Adaptive Wavelet Threshold Rolling Bearing Fault Vibration Signal Denoising Method[J].Journal of Harbin University of Science and Technology， 2021， 26（2）：124.

[4]WICKER H， MLADEN V. INRIA Lectures on Wavelet Packet Algorithms[C]//Proceedings ondelettes et paquets d′ondes， June 17-21， Rocquencourt， France，1991：31.

[5]齐添添，陈尧，何才厚，等.损伤声发射信号小波包神经网络特征识别方法[J].北京邮电大学学报，2021，44（1）：124.

QI Tiantian，CHEN Yao，HE Caihou， et al. Improved Acoustic Emission Signal Wavelet Packet Neural Network Feature Recognition Method[J]. Journal of Beijing University of Posts and Telecommunications， 2021， 44（1）：124.

[6]WALCZAK B， MASSART D L. Wavelet Packet Transform Applied to a Set of Signals： A New Approach to the Best-basis Selection[J]. Chemom.intell.lab.syst， 1997， 38（1）：39.

[7]COIFMAN R R， WICKERHAUSER M V. Entropy-based Algorithms for Best Basis Selection [J]. IEEE Transactio ns on Information Theory， 1992， 38 （ 2 ） ： 713 .

[8]陳东明，朱志良，高晓兴，等.一种最优小波包基搜索算法[J].哈尔滨工业大学学报，2009，41（1）：200.

CHEN Dongming，ZHU Zhiliang，GAO Xiaoxing， et al. A Searching Algorithm Based on the Best Bases of Wavelet Packet[J]. Journal of Harbin Institute of Technology， 2009， 41（1）：200.

[9]SAFARA F， RAMAIAH A R， RENYI B S. Renyi Entropy Basis Sselection from Wavelet Packet Decomposition Tree for Phonocardiogram Classification[J]. The Journal of Supercomputing， 2020（2）.

[10]王嘉乐，王维庆，王海云.基于NLMS-WP及BP的风机轴承故障诊断方法[J].水电能源科学，2021，39（5）：193.

WANG Jiale， WANG Weiqing， WANG Haiyun. Fault Diagnosis of Wind Turbine Bearing Based on NLMS-WP and BP Method[J].Water Resources and Power， 2021， 39（5）：193.

[11]WANG Y S， LIU N N， GUO H， et al. An Engine-Fault-Diagnosis System Based on Sound Intensity Analysis and Wavelet Packet Pre-processing Neural Network[J]. Engineering Applications of Artificial Intelligence， 2020， 94：103765.

[12]WU Fan， WANG Jun， SUN Zhang， et al. An Optimal Wavelet Packets Basis Method for Cascade Hydro-PV-Pumped Storage Generation Systems to Smooth Photovoltaic Power Fluctuations[J]. Energies， 2019， 12.

[13]LIU Tian， XU Tongyu， YU Fenghua， et al. A Method Combining ELM and PLSR （ELM-P） for Estimating Chlorophyll Content in Rice with Feature Bands Extracted by an Improved Ant Colony Optimization Algorithm[J]. Computers and Electronics in Agriculture， 186.

[14]SABRINA M， LEONARDO C T， THOMAS S， et al. A Computational Study on Ant Colony Optimization forthe Traveling Salesman Problem with Dynamic Demands-ScienceDirect[J]. Computers & Operations Research， 2021.

[15]刘浩然，孙美婷，李雷，等.基于蚁群节点寻优的贝叶斯网络结构算法研究[J].仪器仪表学报，2017，38（1）：143.

LIU Haoran， SUN Meiting， LI Lei， et al. Study on Bayesian Network Structure Learning Algorithm Based on Ant Colony Node Order Optimization[J]. Chinese Journal of Scientific Instrument， 2017，38（1）：143.

[16]张宏国，宫雪.Job-shop调度求解的广义蚁群算法[J].哈尔滨理工大学学报，2017，22（1）：91.

ZHANG Hongguo， GONG Xue. A Generalized Ant Colony Algorithm for Job-shop Scheduling Problem[J]. Journal of Harbin University of Science and Technology， 2017， 22（1）：91.

[17]BLANCO S，FIGLIOLA A，QUIROGA R Q，et al. Time-frequency Analysis of Electroencephalogram Series. III. Wavelet Packets and Information Cost Function[J]. Physical Review E Statistical Physics Plasmas Fluids & Related Interdisciplinary Topics， 1998， 51（1）：2624.

[18]BEALE C， NIEZRECKI C， INALPOLAT M.An Adaptive Wavelet Packet Denoising Algorithm for Enhanced Active Acoustic Damage Detection from Wind Turbine Blades[J]. Mechanical Systems and Signal Processing，2020， 142：106754.

[19]LIU Yunxia， LU Xiao， BEI Guangxia， et al. Improved Wavelet Packet Denoising Algorithm using FuzzyTthreshold and Correlation Analysis for Chaotic Signals[J]. Transactions of the Institute of Measurement and Control， 2020， 43（6）：014233122097922.

[20]何江红，李军华，周日贵.参考点自适应调整下评价指标驱动的高维多目标进化算法[J/OL].自动化学报.doi：10.16383/j.aas.c200975.

HE Jianghong， LI Junhua， ZHOU Rigui. Many-Objective Evolutionary Algorithm Driven by Indicator under Adaptive Reference Point Adjustment[J/OL]. Acta Automatica Sinica：doi：10.16383/j.aas.c200975.

（编辑：温泽宇）