基于改进遗传算法的颚式破碎机优化方法研究

孙宇飞　郑晓雯　陈浩　刘肖杉

摘要：针对ANSYS软件自带结构优化算法的不足，将改进的遗传算法应用其中。以颚式破碎机整体结构优化为例，建立基于Solidworks和ANSYS二次开发的颚式破碎机优化平台，分别采用ANSYS软件传统优化算法和内嵌ANSYS有限元分析的改进遗传算法进行优化设计。结果表明：与ANSYS软件自带优化算法相比，改进后的遗传算法在颚式破碎机的整体结构设计中具有明显优势，不仅优化时间大大缩短，优化精度也显著提升。研究结果可为特定零部件的结构优化设计与专用软件开发提供参考。

关键词：颚式破碎机;ANSYS优化;结构优化设计;改进遗传算法;软件开发

DOI：10.15938/j.jhust.2022.02.004

中圖分类号： TD451.2

文献标志码： A

文章编号： 1007-2683（2022）02-0029-07

Optimization of Jaw Crusher Based on Improved Genetic Algorithm

SUN Yu-fei，ZHENG Xiao-wen，CHEN Hao，LIU Xiao-Shan

（School of Mechanical， Electronic and Information Engineering， China University of Mining and Technology （Beijing）， Beijing 100083， China）

Abstract：Aiming at the deficiency of ANSYS′s own optimization algorithm， the improved genetic algorithm is applied to the structural optimization design of ANSYS. Taking the whole structure optimization of jaw crusher as an example， the optimization platform of jaw crusher based on SolidWorks and ANSYS is established.The traditional optimization algorithm of ANSYS and the improved genetic algorithm with embedded ANSYS finite element analysis are used to optimize the design. The results show that compared with the optimization algorithm of ANSYS， the improved genetic algorithm has obvious advantages in the overall structure design of jaw crusher. Not only the optimization time is greatly shortened， but also the optimization accuracy is significantly improved. The research results can provide reference for the structural optimization design and special software development of specific parts.

Keywords：jaw crusher;ANSYS optimal design;structure optimal design;improved genetic algorithms;software development

0引言

颚式破碎机是工程领域应用广泛的破碎设备。国内破碎机的设计仍然偏重传统方法，很难准确设计出既经济又满足使用要求的破碎机[1]。按经验确定各个零部件的形状和尺寸，具有一定的盲目性。很难对主要零部件的整体装配单元进行有效的减重设计优化[2]。

在对复摆颚式破碎机的优化设计研究方面，张希洋[3]研究动颚所受破碎力的变化，并应用到动力学分析及有限元分析中，为破碎机结构优化提供参考。周素琴[4]分析并建立了颚式破碎机破碎原理并进行破碎力仿真研究，对颚式破碎机的关键零件偏心轴、动颚活动齿板座和机架进行仿真分析，为后续破碎机的结构改进提供理论支持和设计方法参考。乔国栋等[5]调用MATLAB优化工具箱的算法，在合理设定的约束条件之下，求解得到颚式破碎机机构优化后的参数，改善了破碎生产率。包从望等[6]以简化后的颚式破碎机破碎机构的杆长和排料口等为设计变量，应用MATLAB遗传算法工具箱进行优化计算，优化后的参数节约了破碎成本，增加了企业效益。

在利用各种软件优点进行设计优化方面已有研究。常凯[7]通过编程实现提高齿轮副啮合特性模型计算的精度和效率。马东辉等[8]提出一种分部优化的设计方法，利用ANSYS进行结构静力学分析，根据结构的受力状况建立优化设计的数学模型，导入到MATLAB优化工具箱对模型进行优化求解，提高了实体优化结果的精确度。Chen等[9]设计出一种基于MATLAB-ANSYS的材料密度优化算法解决了弹性结构拓扑优化的数值困难问题。李珺等[10]提出了参数化建模和仿真分析的框架，将设计人员从重复建模和仿真工作中解放出来。

本文提出一种以颚式破碎机为研究对象的Solidworks-ANSYS集成优化平台。针对应用较为广泛的PEX系列复摆颚式破碎机PEX250×1200建立数学优化模型，使用改进遗传算法优化，优化结果循环导入ANSYS软件中进行受力分析并实时调整。结果表明，较传统的ANSYS优化设计方法，改进后的优化方法的优化效率和求解精度明显提高。

1基于ANSYS的颚式破碎机整体的优化设计

APDL（ANSYS Parametric Design Language）是一种参数化设计语言，可以实现参数化建模、参数化施加载荷、求解及参数化后处理，从而建立优化设计分析文件[11]。由于颚式破碎机整个有限元模型比较复杂，考虑到网格划分精度和优化计算的整体计算量，在保证整体主要零件的设计尺寸精度不发生明显改变的基础上进行适当的简化，略去圆角、倒角、螺纹孔和键槽之类的对结构强度和刚度影响较小的单元。考虑到整体建模计算的难度较大，选取包括偏心轴、动颚和机架3个主要零件进行参数化建模并设置配合关系，轴套则简化为中间件。建立的三維实体模型如图1所示。

颚式破碎机零件的材料选用ZG35，网格划分选三维二次10节点四面体网格，载荷施加在动颚板上，约束施加在机架本体底部。力学模型建立以后需要确定ANSYS优化设计的目标函数和优化参数[12]，其中以破碎机整体的体积V最小为目标函数，目标函数如下：

式中：R为破碎机的偏心轴的外段径;R为内段径;L为偏心轴中段长;R为动颚板的圆环部分外径;L为动颚板平均厚度;L为机架的前后壁厚;L为机架左右壁厚。其设计变量的约束条件如式（3）所示：

式中：F为颚式破碎机整体最大的等效应力;X为颚式破碎机最大变形位移。相关研究表明[[13]：对颚式破碎机的主要零部件组合体进行静力学分析，得到其在一般工况下，动颚体所受的应力最大，位置集中在肘板附近，故取动颚部分材料ZG35的屈服极限255MPa作为整体优化的应力边界条件。动颚体所受最大变形位于动颚体齿面中部的边缘地方，其他部分变形量不大，故取动颚的最大变形量为整体变形的位移边界条件。优化设计的模型建立完成后，使用ANSYS自带优化算法开始优化设计，其优化设计流程图如图2所示。

根据以上数学模型结合颚式破碎机的结构特点，首先利用APDL参数化设计语言创建参数化分析文件，施加边界条件及求解。然后声明优化变量，并确定每个优化变量的上下限和收敛容差，选取零阶优化方法和设定迭代次数，最终循环迭代得到收敛准则下的优化结果。使用传统方法优化前后的结果对比如表1所示。传统优化方法结果表明，在保证机构强度和刚度的基础上，优化后的体积为2.31 m，较优化之前下降了19.8%。

2基于改进遗传算法的颚式破碎机整体结构优化

遗传算法是模拟生物在自然环境下遗传和进化的一种自适应全局优化概率搜索方法。遗传算法的实现主要是通过遗传算子，遗传算子包括：选择算子、交叉算子、变异算子3种[14-15]。选择算子通过选择使最优的个体进入下一代，交叉算子P和变异算子P是通过当代个体交叉和变异形成新的个体。交叉操作是产生新个体的主要操作，决定了遗传算法的全局搜索能力。变异操作是产生新个体的辅助性操作，决定遗传算法的局部搜索能力。

交叉算子P过大会破坏遗传模式，过小又会使整个搜索过程缓慢;变异算子P过大会导致搜索精度剧烈下降，过小不容易产生新的个体，局部寻优能力差[16]。为解决上诉问题，遗传算法研究者们尝试在遗传算法的种群多样性[17-19]和交叉、变异[20]过程进行改进设计。本文是在一般遗传算法的交叉、变异过程中采用自适应的交叉算子和变异算子，其主要思想是：对于适应度高于群体平均适应度的个体，选择较低的交叉算子P和变异算子P，使个体被破坏的可能性尽可能减小;对于适应度低于种

群平均值的个体，选择较高的交叉算子P和变异算子P，淘汰掉较差的个体产生新的个体，保证了算法的收敛性。线性自适应遗传算法中交叉概率和变异概率的相应函数表达式如下：

式中：P和P为自适应遗传算法下个体的交叉概率和变异概率;f和f分别表示种群的平均适应度值和最大适应度值;P和P分别表示交叉算子的上限值和下限值;P和P分别表示变异算子的上限值和下限值;f和f′分别表示种群需要交叉和变异个体的适应值。

式（5）和（6）中线性函数的梯度值为：

将式（7）中的线性函数的交叉梯度值x和变异梯度值x分别引入到双曲余弦和双曲正切函数中即可得到改进的双曲余弦自适应遗传算法和双曲正切自适应遗传算法。双曲余弦自适应遗传算法的交叉概率和变异概率的函数表达式如下：

同理，双曲正切自适应遗传算法的交叉概率和变异概率的函数表达式为

自适应算法对应的交叉变异概率值变化如图3所示。

图3中如果个体的适应度值小于平均值，其交叉概率和变异概率较大，能够尽快的淘汰落后的个体;如果个体的适应度大于平均值，其交叉概率和变异概率随着个体适应度值的增大而减小，降低了每代中优秀个体被破坏的可能性。通过个体的适应度值自适应调节变异算子的大小实现种群的自适应优化。选用线性函数的自适应遗传算法对处于进化后期的群体比较合适，但对于进化初期群体不利;选用双曲正弦函数的自适应遗传算法对于进化初期比较合适，但后期的群体精度较差;选用双曲正切函数的自适应遗传算法在群体进化初期收敛较快，但后期容易陷入局部最优值。需根据实际情况选用相应的自适应函数以适应不同的函数，进而保证种群进化的收敛速度和精度。

为进一步提高遗传算法优化的准确度，将ANSYS结构计算分析嵌入到遗传算法的优化迭代中。将每一代适应度最大的个体还原成各个设计变量，导入到ANSYS中进行参数化建模设计并进行有限元分析，输出后处理得到的状态变量。将状态变量输入到遗传算法的迭代过程中，如果状态变量不满足设置条件，则剔除不合格的个体，并修改相应的设计变量范围以达到合理监管设计变量的目的。

具体算法实现流程图如图4所示：

根据图4中遗传算法实现流程图，优化开始以后，设计人员初始化变量范围并选择相应的遗传算法，计算出初始值并导入ANSYS进行有限元分析。

ANSYS软件根据导入的值进行参数化建模并进行静力学分析，提取计算后的状态变量和设定的许可值进行比较。状态变量值在许可范围内时，根据选择的遗传算法和设定算子值等进行优化获得当前次数最优解并循环执行遗传优化算法，否则改变各设计变量值防止出现不符合要求的变量值并重新执行遗传优化算法。

在状态变量许可的范围内优化算法循环达到设定的收敛条件后，循环结束得到最优解的优化个体并输出设计变量。采用线性自适应算子的改进遗传算法得到的优化结果如表2所示。结果表明，在保证机构强度和刚度的基础上，优化后的体积为2.07m，较优化之前下降了28.1%。

3传统算法和改进遗传算法优化过程分析

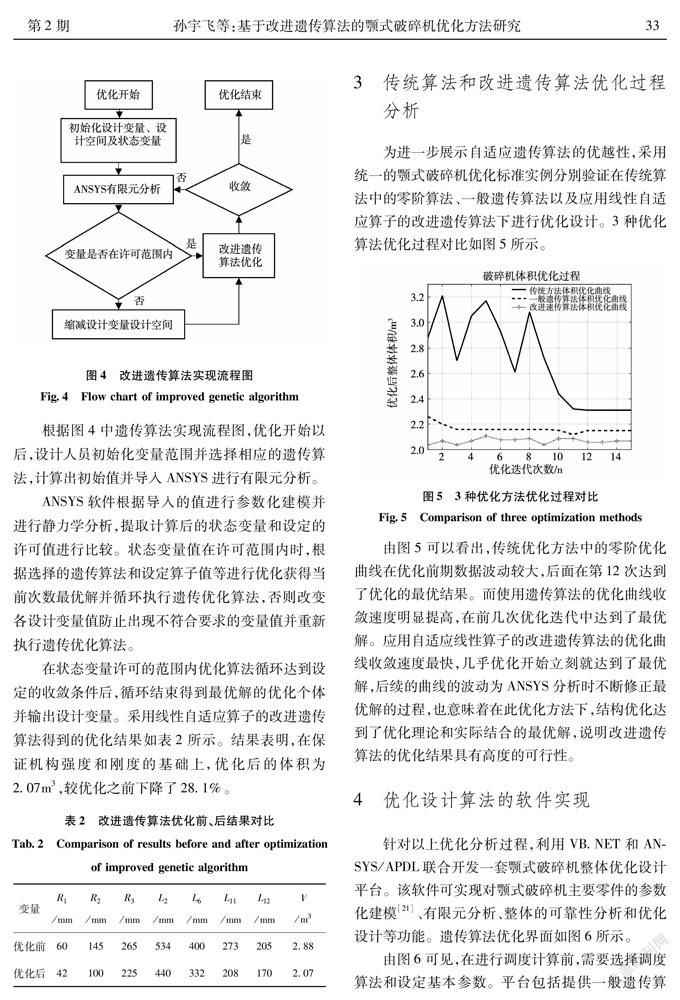
为进一步展示自适应遗传算法的优越性，采用统一的颚式破碎机优化标准实例分别验证在传统算法中的零阶算法、一般遗传算法以及应用线性自适应算子的改进遗传算法下进行优化设计。3种优化算法优化过程对比如图5所示。

由图5可以看出，传统优化方法中的零阶优化曲线在优化前期数据波动较大，后面在第12次达到了优化的最优结果。而使用遗传算法的优化曲线收敛速度明显提高，在前几次优化迭代中达到了最优解。应用自适应线性算子的改进遗传算法的优化曲线收敛速度最快，几乎优化开始立刻就达到了最优解，后续的曲线的波动为ANSYS分析时不断修正最优解的过程，也意味着在此优化方法下，结构优化达到了优化理论和实际结合的最优解，说明改进遗传算法的优化结果具有高度的可行性。

4优化设计算法的软件实现

针对以上优化分析过程，利用VB.NET和ANSYS/APDL联合开发一套颚式破碎机整体优化设计平台。该软件可实现对颚式破碎机主要零件的参数化建模[21]、有限元分析、整体的可靠性分析和优化设计等功能。遗传算法优化界面如图6所示。

由图6可见，在进行调度计算前，需要选择调度算法和设定基本参数。平台包括提供一般遗传算法、线性自适应遗传算法、双曲正弦自适应遗传算法和双曲正切自适应遗传算法4种算法，并根据需要由操作人员确定是否引入ANSYS有限元分析，并给出了相关参数的建议范围，最后整个优化进程的结果显示在右侧的列表中。引入遗传算法的优化设计系统不仅提高了优化效率和优化结果精度，也进一步减轻了设计人员的操作难度。

5结语

1）根据颚式破碎机结构特点，开发基于Solidworks和ANSYS的颚式破碎机设计优化平台，结合ANSYS/APDL参数化设计语言完成对于颚式破碎机主要零部件机架、动颚和偏心轴的组合体建模并生成循环所用的优化分析文件，通过设定参数变量和声明优化变量，完成基于ANSYS自带优化算法的颚式破碎机整体的结构优化设计。

2）在颚式破碎机自带优化算法存在不足的前提下引入遗传算法，提出了基于遗传算法优化、ANSYS有限元分析的改进优化算法，并应用于实际工程的仿真优化中，取得了较为理想的结果。

3）为保证遗传算法在保持种群多样性的同时，提供相对优秀的个体解，在一般遗传算法的基础上引入不同的自适应遗传算子，增加线性自适应遗传算法、双曲正弦自适应遗传算法和双曲正切自适应遗传算法。结果表明，采用自适应遗传算法较一般遗传算法的收敛速度更快、收敛精度更高。

参 考 文 献：

[1]陈立春， 薛俊芳， 张秀芬， 等. 颚式破碎机动颚轻量化优化[J].煤炭工程， 2018， 50（8）： 164.CHEN Lichun， XUE Junfang， ZHANG Xiufen， et al. Lightweight Optimization for the Movable Jaw of Crusher[J]. Coal Engineering， 2018， 50（8）： 164.

[2]CAYIROGLU I， KILIC R. Wing Aerodynamic Optimization by Using Genetic Algoritm and Ansys[J]. Acta Physica Polonica A， 2017， 132（3）： 981.

[3]張希洋. 复摆颚式破碎机动力学及有限元分析[D].太原：太原理工大学， 2015.

[4]周素琴. 基于运动学和有限元分析的颚式破碎机结构改进的研究[D].昆明： 昆明理工大学， 2014.

[5]乔国栋， 胡俊波， 赵杰. PEX250x1000型细碎复摆式破碎机主要机构的优化设计[J].机械制造， 2015， 53（7）： 31.QIAO Guodong， HU Junbo， ZHAO Jie. Optimization Design of Main Mechanism of PEX250x1000 Fine Crushing Compound Pendulum Crusher[J]. Machinery， 2015， 53（7）： 31.

[6]包从望， 江伟. 基于遗传算法颚式破碎机结构优化[J].煤矿机械， 2019， 40（2）： 111.BAO Congwang， JIANG Wei. Structure Optimization of Jaw Crusher Based on Genetic Algorithm[J]. Coal Mine Machinery， 2019， 40（2）： 111.

[7]常凯. 一种渐开线齿轮啮合特性分析的参数化求解方法研究[J].机械工程师， 2017（8）： 94.CHANG Kai. Research on Parameterized Method for Meshing Characteristics Analysis of Involute Gear[J]. Mechanical Engineer，2017（8）： 94.

[8]马东辉， 赵东. 基于ANSYS和MATLAB的结构优化设计[J].制造业自动化， 2013， 35（10）： 106.MA Donghui， ZHAO Dong. Optimal Structural Design Based on ANSYS and MATLAB[J]. Manufacturing Automation， 2013， 35（10）： 106.

[9]CHEN Qi， ZHANG Xianmin， ZHU Benliang. A 213-line Topology Optimization Code for Geometrically Nonlinear Structures[J]. Structural and Multidisciplinary Optimization， 2019， 59（5）： 1863.

[10]李珺， 杨扬. 基于Solidworks-MATLAB-ANSYS集成框架的结构优化设计[J].计算机应用与软件， 2020， 37（3）： 8.LI Jun， YANG Yang. Structural Design Optimization Based on SolidWorks-MATLAB-ANSYS Integrated Framework[J]. Computer Applications and Software， 2020， 37（3）： 8.

[11]刘朋， 郑园园， 汤宝石， 等. 基于ANSYS的O形密封圈可靠性分析及软件开发[J].液压气动与密封， 2020， 40（5）： 11.LIU Peng， ZHENG Yuanyuan， TANG Baoshi， et al. Reliability Analysis and Software Development of O-ring Based on ANSYS[J]. Hydraulics Pneumatics and Seals， 2020， 40（5）： 11.

[12]FLADVAD M， ONNELA T. Influence of Jaw Crusher Parameters on the Quality of Primary Crushed Aggregates[J]. Minerals Engineering， 2020， 151. doi： 10.1061/ j.mineng.2020.106338.

[13]许北俊， 胡俊光， 叶爽. PEX150x750细碎颚式破碎机运动学仿真及有限元分析[J].南华大学学报（自然科学版）， 2018， 32（1）： 87.XU Beijun， HU Junguang， YE Shuang. Kinematics Simulation and Finite Element Analysis of PEX150×750 Fine Jaw Crusher[J]. Journal of University of South China（Science and Technology）， 2018， 32（1）： 87.

[14]彭雄凤. 基于改进遗传算法的车间调度问题的研究[D].昆明： 昆明理工大学， 2009.

[15]马永杰， 云文霞. 遗传算法研究进展[J].计算机应用进展， 2012， 29（4）： 1201.MA Yongjie， YUN Wenxia. Research Progress of Genetic Algorithm[J]. Application Research of Computers， 2012， 29（4）： 1201.

[16]唐文艳， 顾元宪. 遗传算法在结构优化中的研究进展[J].力学进展， 2002， 32（1）： 26.TANG Wenyan， GU Yuanxian. Advances of Genetic Algorithms in Structural Optimization[J]. Advances in Mechanics， 2002， 32（1）： 26.

[17]JAFARI S A， MASHOHOR S， VARNAMKHASTI M J. Committee Neural Networks with Fuzzy Genetic Algorithms[J]. Journal of Petroleum Science and Engineering， 2011， 76（3）： 217.

[18]马浩兴， 王东红， 罗文龙. 基于多种群遗传算法的液压系统PID参数寻优[J].包装工程， 2020， 41（23）：204.MA Haoxing， WANG Donghong， LUO Wenlong. PID Parameter Optimization of Hydraulic System Based on Multi-population Genetic Algorithm[J]. Packaging Engineering[J]. 2020， 41（23）： 204.

[19]白永明， 陶藝， 吴迎春，等. 基于改进NSGA2算法的航空燃油泵叶轮优化设计[J].兵器装备工程学报， 2020， 41（12）： 132.BAI Yongming， TAO Yi， WU Yingchun ，et al. Optimization Design of Aviation Fuel Pump Impeller Based on Improved NSGA2 Algorithm[J].Journal of Ordnance Equipment Engineering， 2020， 41（12）： 132.

[20]RAJAKUMAR B R，GEORGE A. A New Adaptive Mutation Technique for Genetic Algorithm[C]// International Conference on Computational Intelligence and Computing Research （ICCIC）， Coimbatore， India， 2012： 1.

[21]赵彦玲， 王崎宇， 鲍玉冬， 等. 基于VB的钢球自动检测系统参数化设计[J].哈尔滨理工大学学报， 2020， 25（5）： 120.ZHAO Yanling， WANG Qiyu， BAO Yudong， et al. Parametric Design of Steel Ball Automatic Detection System Based on VB[J]. Journal of Harbin University of Science and Technology， 2020， 25（5）： 120.

（编辑：温泽宇）