铰削过程有限元仿真及优化

岳彩旭　胡德生　张安山　刘献礼　刘智博　陈志涛

摘要：在发动机气门导管加工过程中，焊接式铰刀几何参数对铰削过程中切削力、切削温度、刀具损伤等有显著影响。提出一种结合快速参数化建模、有限元仿真及多目标优化的试验方法来得到最优的刀片几何参数。首先通过Python语言进行刀片和工件几何参数化建模的二次开发;其次采用单因素试验法分析不同刀片几何参数对切削力、切削温度的影响趋势;最后结合正交试验法与响应曲面法建立了以切削力及切削温度为目标的函数，通过Fmincon优化模型得到刀片几何参数最优解。该研究方法有效的提高了刀具设计的效率，并对焊接式铰刀几何结构设计具有重要指导意义。

关键词：铰削过程;有限元仿真;刀片结构;多目标优化;Fmincon优化模型

DOI：10.15938/j.jhust.2022.02.001

中图分类号： TG501

文献标志码： A

文章编号： 1007-2683（2022）02-0001-09

Finite Element Simulation and Optimization of Reaming Process

YUE Cai-xu，HU De-sheng，ZHANG An-shan，LIU Xian-li，LIU Zhi-bo，CHEN Zhi-tao

（Key Laboratory of Advanced Manufacturing and Intelligent Technology， Ministry of Education，

Harbin University of Science and Technology， Harbin 150080， China）

Abstract：In the engine valve guide machining process， the geometric parameters of the welded reamer have a significant effect on the cutting force， cutting temperature， tool damage， etc. during the reaming process. A test method combining fast parametric modeling， finite element simulation and multi-objective optimization is proposed to obtain the optimal blade geometric parameters. Firstly， the secondary development of blade and workpiece geometric parameter modeling is carried out through Python language; secondly， single factor experiment method is used to analyze the influence trend of different blade geometric parameters on cutting force and cutting temperature; finally， the orthogonal experiment method and response surface method are combined to establish a function with cutting force and cutting temperature as the objective is obtained， and the optimal solution of insert geometric parameters is obtained through the Fmincon optimization model. This research method effectively improves the efficiency of tool design and has important guiding significance for the geometric structure design of welded reamer.

Keywords：reaming process; finite element simulation; blade structure; multi-objective optimization; Fmincon optimization model

0引言

鉸削加工工艺在航天、汽车、船舶、核电等领域得到广泛应用，尤其在对发动机缸盖气门导管的加工过程中，铰削工艺显得尤为重要。铰削加工工艺的重点在于随时间的改变径向力及切向力的方向不断改变，导致在铰削过程中切削力不稳定，影响刀具使用寿命，为了解决该问题，对刀具结构的优化显得尤为重要。

国内外大量学者以实验法对铰削加工进行研究，例如Yin等[1]使用AdvantEdge有限元仿真软件对航空铝合金用PCD铰刀铰削加工过程进行仿真分析，研究主轴转速、每齿进给量对切削力和切削温度的影响。Schutzer等[2]探究了气门导管铰刀在铰孔过程中出现的加工误差和不同刀具几何结构对铰孔质量的影响。Pilny等[3]分别以矿物纯油和水基润滑剂为切削液对奥氏体不锈钢进行铰削试验，得到不同切削液对铰孔质量的影响。大连工业大学韩鹏亮[4]研究了复合铰刀前角对切屑形态的影响。试验结果表明：复合铰刀的前角变化对于切屑形态有较大的影响，前角过小容易形成积屑瘤，导致切屑形态变化较大;前角过大导致刀具稳定性较差、铰削过程易产生振动，导致切屑较碎。宁世有等[5]对直刃铰刀、斜刃铰刀、螺旋刃铰刀进行了干式铰削试验研究，在大量实验数据的基础上对3种刃形铰刀在铰削力、表面粗糙度、切屑形状方面进行了对比评判，优化出使用效果最佳铰刀为螺旋刃铰刀。鲁柱[6]对不锈钢车削、磨削、钻削、铰削的冷切削加工技术进行研究，针对铰削提出：铰削余量不能太大，粗铰0.15～0.3mm，精铰0.1～0.15mm，铰削v≤12m/min，f为0.1～0.3mm/r。王志刚等[7]采用直刃铰刀、斜刃铰刀、螺旋刃铰刀对电站设备的零部件进行了干式铰削试验研究，并对以上3种铰刀的铰削力、表面粗糙度、切屑形貌做出模糊综合评判，最终得出螺旋刃铰刀的使用效果最佳。许小村等[8]开发出一种胶接式气门座铰刀，并对焊接气门座铰刀与胶接气门座铰刀安排切削对比试验。试验结果表明，与焊接气门座铰刀相比，胶接气门座铰刀的切削力小，刀具寿命长，且被加工工件的表面粗糙度值小。

此外国内外部分学者采用仿真方法对铰削加工进行研究，例如Towfighian等[9]采用有限元仿真模拟在某些骨科铰孔手术中导致形成多形孔或非圆柱孔的铰削模型，并改善了铰孔质量。Horst等[10]采用有限元仿真的方法对自增强后的残余应力深度进行铰孔模拟，并通过实验采用X射线法测量残余应力，进而验证仿真的准确性。Yang等[11]为了研究磨削铰孔中毛刺的形成机理，建立了单颗粒磨料的微切削模型来模拟毛刺的形成。吉林大学王大明[12]利用Advantedge FEM有限元仿真软件，将三维铰削有限元模型简化成二维车削有限元模型对发动机气门座圈加工工艺进行仿真分析，对比不同进给速度和主轴转速下的切削力、切削温度以及应力应变的变化趋势，得到最佳的进给速度和主轴转速搭配方案。浙江大学高凯晔[13]利用ABAQUS有限元仿真软件，以螺旋铣孔刀具的一个刀齿作为研究对象，以轴向力为主要评判标准，研究了不同刀具角度对切削力的影响规律，发现影响轴向力的主要因素依次为刀具前角、V型刃夹角、V型刃倾斜角。李玉平等[14]以YT5类硬质合金刀具切削45钢为研究对象，基于ANSYS软件建立了金属二维正交切削过程的有限元模型，并以刀具受力最小为优化目标对刀具参数进行了优化，得到以下结论：YT5类硬质合金刀具切削45钢，宜采用前角为3°和后角为5°的刀具，刀具在稳定切削状态下的应力最小，抗破损能力最好，磨损最少。

现如今对于铰削加工过程的研究大多以传统试验为主，通过大量试验数據对刀具角度及加工参数进行优化，但该方式具有试验成本高、周期长、效率低等局限性。因此，部分学者采用有限元仿真方法对铰削过程进行研究，但在研究过程中都使用将三维铰削仿真模型简化为二维斜角切削的方法进行研究，此方法无法考虑径向力和切向力的时变特性，所获得的仿真切削力与切削温度等结果与实际工况相比存在较大偏差。因此，以提高仿真精度为目的，本文进行了考虑径向力和切向力时变特性的灰铸铁气门导管三维铰削有限元仿真研究，并且为了使刀具设计周期缩短，降低设计成本，提出一种以UG19.4为基础，联合PyQt可视化模块的刀具参数化建模方法。通过以上方法获得了不同刀具几何参数对切削力、切削温度的影响，并对刀具几何参数进行优化设计。本文提出的参数化建模方法及三维有限元仿真方法对焊接式铰削刀片的结构设计具有重要的指导意义。

1仿真模型的建立

焊接刀片的设计成本高、实验周期长，为节约设计成本，缩短设计、实验周期，提高设计效率，采用UG与PyQt相结合的方法，实现刀片和工件参数化建模，再将刀片与工件导入ABAQUS中进行铰削仿真。

1.1基于UG的刀具及工件结构参数化设计

建立刀片与工件参数化建模系统是由西门子（Siemens PLM Software）公司的UG19.4软件与PyQt联合所制作。在UG19.4中以表达式形式建立刀片与工件结构模型，使用UG软件中录制工具对表达式程序（即内核程序）进行录制;然后在Qt Designer中建立刀具与工件参数化界面，如图1（a）和（b）所示，利用PyUIC将参数化界面转换为.py程序;编写bat文件使PC端自动打开UG软件并运行内核程序;最后将表达式程序与bat程序嵌入.py程序中，通过在界面中修改刀具与工件结构参数，即实现快速、高速的参数化建模。通过使用该参数化建模方法，可极大缩短产品设计周期与研发周期、降低研发成本。并且，所建立刀具模型与实物相比高度一致。该参数化设计方式摆脱了传统参数化设计方式，即使用PyQt制作参数化界面，并且所设计的参数化界面具有较好的人机交互功能。铰刀实物图和绘制的铰刀模型如图2（a）和（b）所示。

实验采用的刀片和工件如图3中a）和b）所示。刀片前角0°、后角4°、主偏角65°;工件长度3mm、内径6.8mm、外径12mm、加工直径7.75mm。将刀片模型、工件模型和刀杆模型以STEP格式导入ABAQUS中对其进行装配，有限元几何模型装配图如图4所示。为增加仿真结果准确性，设置刀杆为显示体，刀片为刚体;刀片网格属性为六面体扫掠网格（C3D8T），工件网格属性为六面体结构网格（C3D8RT）;使工件底部完全固定，刀具以进给速度96mm/min、主轴转速1196r/min为边界条件进行铰削加工仿真分析。

1.2本构模型

材料的本构模型能反映材料形变过程中流动应力等的变化，而正确合适的本构模型决定了仿真结果的准确性[15]。工件材料为灰铸铁，由于其具有高应变、高应变率、高温等特性，因此采用Johnson-Cook本构方程描述其在切削状态下的材料属性，表达式如下：

1.3刀-屑接触摩擦模型

在铰削加工过程中，刀具和工件间的摩擦接触对加工精度、表面质量、刀具磨损等有着重要影响。Zorev对刀-屑间表面常态和摩擦应力提出了真实表述。刀-屑接触区域分为粘结区域和滑动区域两区域[17]。两部分所占比例与刀-屑摩擦系数的设定相关，粘结区认为剪应力是固定值，与材料的屈服应力相等，滑动区摩擦系数满足库伦摩擦定律，为常数。摩擦模型方程见式（2）。

式中：σ为法向应力;τ为材料剪切流动应力;u为摩擦系数。

1.4热传导模型

在铰削加工过程中，由于刀具-工件接触表面的材料塑性变形和摩擦影响，导致切削区域温度不断增加。切削过程所产生的绝大多数的热量通过切屑带走，还有部分热量被传导到空气中。为了提高分析的准确性，传导到空气中的热量可以用式（3）进行表述[18]。

Q=h×（T-T） （3）

式中：h为对流换热系数;T为刀具和工件的表面温度;T为室温。

2铰削过程有限元仿真分析

由于三维铰削仿真更加贴近真实切削工况，因此对切削过程应力场、温度场的分析以及得到的三向切削力变化规律精准度更高。

2.1切削过程应力场分析

刀具的几何结构影响着刀具稳定性与加工精度等，同时也影响着工件的应力场分布、刀具的温度场分布。

以0°前角、4°后角、65°主偏角的金刚石铰刀刀片为例，切削参数不变。如图5（a）、（b）、（c）所示为刀具切入状态、切削状态、切削完成状态的工件加工表面Mises应力分布云图。

如图5（a）所示，当刀片切入工件时，对工件产生冲击力，此时工件所能承受的最大应力超过了屈服极限，工件开始产生塑性变形。如图5（b）所示，切削进入稳定状态，此时刀具前刀面与工件第一接触区处应力最大，达到1127MPa，此刻工件达到切屑分离极限后开始产生切屑。如图5（c）所示，当切削过程完成后，此刻工件表面应力分布均匀。

2.2切削过程温度场分析

在切削过程中，工件与前刀面接触产生的摩擦作用、刀具后刀面和已加工表面的摩擦作用导致切削热的产生。另外，刀具表面所受热-力耦合作用导致刀具磨损的生成，若刀具磨损较大，对加工表面精度产生极大影响，因此，对切削过程温度场进行分析具有重要意义。图6为切削过程中某一刻工件与刀具的温度分布云图。可以看出，切屑的温度高于刀片和工件已加工表面的温度，这说明灰铸铁在切削过程中，切屑带走大部分热量。

图7为工件已加工表面温度分布云图。热量主要来自2个方面，一是在刀片与工件接触的变形区，在该处材料发生剧烈塑性变形，使很大一部分能量转化为热能。二是切屑沿前刀面快速流出，由于摩擦产生大量的热来不及冷却，使已加工区域温度迅速升高。

可以看出前刀面与切屑接触区域温度最高，可达221.7℃。已加工表面与后刀面由于摩擦产生热量，温度分布区域为137.6～204.9℃，并随着切削的进行温度逐渐降低。

2.3切削力仿真结果

刀具切削工件易产生较大切削力，由于切削力不稳定或切削力突变将导致工件振动、变形、稳定性差等问题，进而减低工件表面尺寸精度，使工件不能达到标准要求。因此，稳定的切削力有利于提高已加工表面精度，延长刀具使用寿命。提取铰削过程中3个方向x、y、z的切削力值，如图8所示。

由图8可以看出，F和F呈周期性变化，F几乎不变，這主要因为刀片沿径向和切向做圆周运动，而沿轴向做直线运动。轴向为刀具进给方向，而切削刃主要沿径向和切向切削工件，因此径向力和切向力较大，轴向力较小。由于在初始切削位置径向与切向存在90°相位差，导致切削周期不同。在切削仿真过程中，网格会产生畸变，从而导致某一点的切削力产生突变。

3刀具几何参数对切削过程的影响

由于刀具后角对刀具后刀面磨损、加工精度等产生重要影响，刀具主偏角对切削稳定性产生重要影响。刀具后角过小将导致刀片强度不够;刀具后角过大将导致后刀面磨损量变大，影响刀具使用寿命;刀具主偏角过小导致切削刃缩短，影响切削效率;刀具主偏角过大导致刀-屑接触面积增加，导致摩擦生热增加。因此本文选择0°前角，4°、6°、8°、10°的后角，与65°、70°、75°、80°主偏角的刀片为研究对象，仿真参数不变，并对仿真结果进行单因素与正交分析，得到切削力、切削温度随刀具角度增大的变化规律及以单因素优化的最优搭配。

3.1刀具几何参数对切削力的影响规律

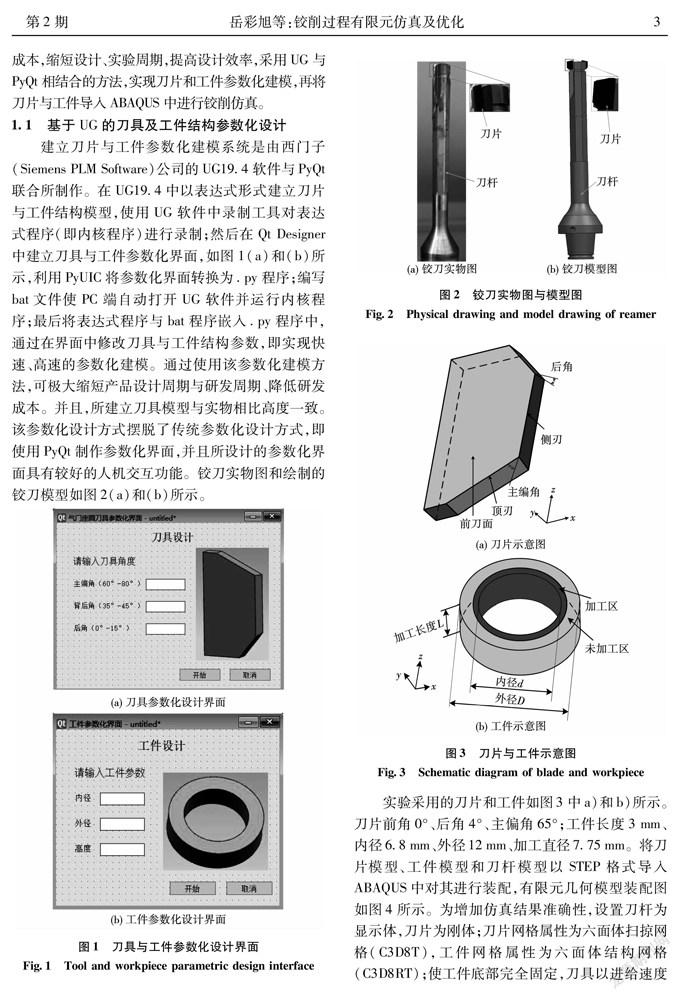
通过对仿真结果后处理，选取x、y方向切削力波峰均值为研究对象。由图8可以看出，z轴切削力小且几乎稳定不变，因此不做分析。当主偏角为75°时，后角增大，通过有限元仿真得到的切削力变化趋势如图9所示。

分析图9可知后角增大，径向力F、切向力F的大小均减小。因为后角增大，刀刃变得更锋利，刀具后刀面与工件间的摩擦减小，切入待加工表面更容易，刃口对工件的挤压变小，已加工工件表面硬化程度下降，因此F、F均有减小趋势。

当后角为8°时，主偏角增大，通过有限元仿真得到的切削力变化趋势如图10所示。

分析可知主偏角增大，径向力F增大、切向力F几乎不变，这说明主偏角对径向力影响显著，对切向力影响不大。随着主偏角的增大，切削刃变长，刀-工件接触面积增加，使工件作用于刀尖处切削力增大，随之刀具振动增大，将影响刀具切削效率和刀具抗震性。所以，不宜选择较大主偏角。

3.2刀具几何参数对切削温度的影响规律

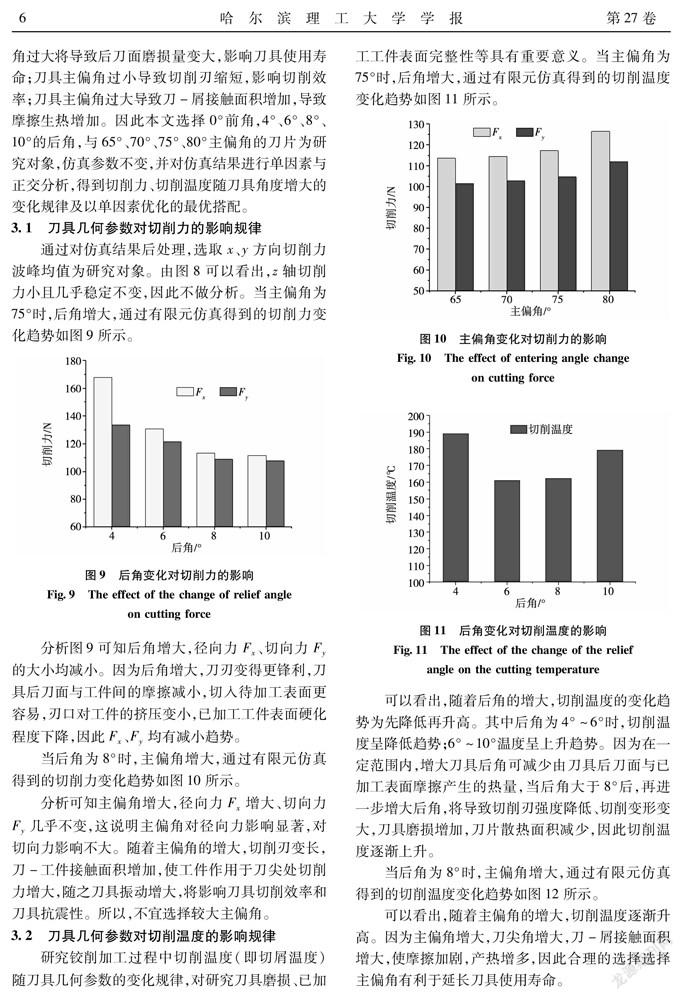
研究铰削加工过程中切削温度（即切屑温度）随刀具几何参数的变化规律，对研究刀具磨损、已加工工件表面完整性等具有重要意义。当主偏角为75°时，后角增大，通过有限元仿真得到的切削温度变化趋势如图11所示。

可以看出，随着后角的增大，切削温度的变化趋势为先降低再升高。其中后角为4°～6°时，切削温度呈降低趋势;6°～10°温度呈上升趋势。因为在一定范围内，增大刀具后角可减少由刀具后刀面与已加工表面摩擦产生的热量，当后角大于8°后，再进一步增大后角，将导致切削刃强度降低、切削变形变大，刀具磨损增加，刀片散热面积减少，因此切削温度逐渐上升。

当后角为8°时，主偏角增大，通过有限元仿真得到的切削温度变化趋势如图12所示。

可以看出，随着主偏角的增大，切削温度逐渐升高。因为主偏角增大，刀尖角增大，刀-屑接触面积增大，使摩擦加剧，产热增多，因此合理的选择选择主偏角有利于延长刀具使用寿命。

3.3正交试验分析结果

采用正交试验能够用较少的试验找到因素水平间的最优搭配。以刀片后角和主偏角为因素建立2因素4水平L（4）的正交表如表2所示。

为分析刀片后角、主偏角对铰削过程的影响，把仿真结果所获得的F和F波峰均值的切削合力和切削温度（即最高切屑温度）进行极差分析。通过极差分析明确不同因素对指标影响程度的主次顺序和因素的最优水平组合。

将铰削有限元仿真得到的F和F波峰均值的切削合力和切削温度进行极差分析，结果见表3和表4。其中k、k、k、k分别对应不同因素4个水平的平均值，F表示F和F波峰均值的切削合力，T表示切削温度（即最高切屑温度），R表示因素的极差值（即R=k-k），通过比较R值大小可得到后角与主偏角对F或T影响程度的大小。

由表3可以看出：焊接式刀片角度对切削力的影响程度大小为后角大于主偏角。结合表2，从减小切削力的角度，最优解为后角8°，主偏角65°。

由表4可以看出：焊接式刀片角度对切削温度影响程度大小为后角大于主偏角。结合表2，从减小切削温度的角度，最优解为后角6°，主偏角65°。

4综合考虑切削力和切削温度的刀片参数优化

本文所研究的是关于焊接式铰刀刀片结构优化问题，基于切削力和切削温度2个目标函数，得到刀片后角和主偏角的多目标优化函数。多目标优化模型通常包括目标函数、优化变量及其相应的约束条件，三者之间具有一定的函数关系，关系式为[19]：

y=F（x）=（f（x）， f（x），L f（x））x≤Ω （4）

式中：y为目标函数;x为优化变量;Ω为约束条件。

本文所求解的是带约束的非线性多变量函数的

最小值问题，采用Fmincon优化算法。该算法是求解非线性有约束极值优化问题的一个有效方法，也可用来求解线性规划、非线性规划和多目标规划等优化问题。

4.1目标函数的建立

应用响应面分析法（RSM）获得目标函数，选择刀片后角和主偏角作为变量，变量及其数据在表3中给出。RSM数学模型为[20]：

式中：Y是预测响应;β是常数项;β是线性響应;β是相互作用响应;β是平方响应。

对于2个变量输入参数x和y（其中x代表刀片后角，y代表刀具主偏角）和目标函数Y可以调整为：

Y=β+βx+βy+βx+βy+βxy （6）

使用MATLAB软件拟合出关于切削力F与切削温度T的公式如下：

F=-53.52-37.66x+9.281y+1.403x-0.069 5y+0.209 8xy （7）

T=625.6-29.16x-10.48y+1.461x+0.070 75y+0.114 7xy （8）

求解多目标优化问题的方法有多种，其中评价函数法应用最广泛，该方法是将多个需要优化的目标函数通过分配权重的方式转化为单目标函数，以便求取最优解。加权系数的值代表所对应子目标的重要程度，本文的优化目标是寻找使切削力和切削温度最小的刀片结构参数后角和主偏角。设定切削力和切削温度的加权系数均为0.5[21]，设定约束条件为后角范围为4°～10°，主偏角范围为65°～80°，综合优化目标函数可表示为：

Z=0.5F+0.5T（9）

4.2刀片结构优化结果

加工条件不变，以加权后函数的最小值为优化目的，对所建立的式（9）模型经过优化求解，可以得到目标函数最优解的具体数值及三维变化图，其优化结果如图13所示。

考虑到刀具磨制难度，最终优化结果取近似整数。可以看出刀片结构最优解为：后角8°，主偏角65°。

4.3最优解对比分析

根据表5可得，以最小切削力为优化目标时最优刀具几何结构为后角8°，主偏角65°;以最小切削温度为优化目标时最优刀具几何结构为后角6°，主

偏角65°;综合考虑切削力和切削温度时最优刀具几何结构为后角8°，主偏角65°。

由表3可知，当后角8°，主偏角65°时切削力为152.6N，切削温度为159.4℃;当后角6°，主偏角65°时切削力为163.7N，切削温度为156.6℃。综合对比以上2种情况的切削力与切削温度数值，可以得出，当后角8°，主偏角65°时切削力、切削温度值均为最小。因此，在使用刀片对气门导管加工时，推荐使用后角8°、主偏角65°的刀片。

5结论

以UG19.4为基础，联合PyQt可视化模块对刀片、工件几何结构进行建模;考虑径向、切向切削力时变特性，建立灰铸铁气门导管三维铰削仿真模型;对切削过程应力场、温度场进行分析;通过仿真实验结果获得不同刀具几何参数对切削力、切削温度的影响，并对刀具几何参数进行优化设计。随刀具几何结构改变，得到切削力、切削温度的变化规律具体如下：

1）随着后角的不断增加，铰削过程中的径向力F、切向力F都有所减小;随着主偏角的不断增加，铰削过程中的径向力F有所增大、切向力F几乎不变。随着后角的增大，铰削过程中的切削温度先降低再升高;随着主偏角的增大，切削温度逐渐升高。

2）通过正交试验和极差分析可得，焊接式刀片角度对切削力和切削温度的影响程度大小均为后角大于主偏角。若以减小切削力为目的，刀片角度最优的搭配组合为后角8°，主偏角65°;若以减小切削温度为目的，刀片角度最优的搭配组合为后角6°，主偏角65°。

3）基于Fmincon优化算法，以综合考慮切削力和切削温度为优化目标，刀具结构参数最优解为后角8°，主偏角65°。

参 考 文 献：

[1]YIN J， YANG W， WANG Y G. Simulation Analysis of Aviation Aluminum Alloy Reaming Processes by Using PCD Reamer[J]. Key Engineering Materials，2020（866）：3.

[2]SCHUTZER K， ROTH M， ABELE E， et al. Experimental investigation of Hole Quality During Reaming Applications Using Multi-Blade Tools[J]. Journal of the Brazilian Society of Mechanical Sciences and  Engineering，2014，36（4）：797.

[3]PILNY L， MULLER P， CHOIFFRE L D. Reproducibility of A Reaming Test[J]. International Journal of Manufacturing Research，2014，9（2）：157.

[4]韩鹏亮.加工碳钢用复合铰刀前角的实验研究[D].大连：大连工业大学，2015.

[5]宁世友， 程耀楠， 王志刚， 等. 铰削试验研究和铰刀优化[J].黑龙江工程学院学报， 2005， 19（1）： 1.

NING Shiyou， CHENG Yaonan， WANG Zhigang， et al. The Reaming Experiment Research and ReamerOptimization[J]. Journal of Heilongjiang Institute of Technology， 2005， 19（1）： 1.

[6]鲁柱. 不锈钢冷切削加工技术的应用研究[J].现代制造技术与装备， 2019， 277（12）： 129.

LU Zhu. Research on Cold Cutting Technology Application of Stainless Steel[J]. Modern Manufacturing Technology and Equipment， 2019， 277（12）： 129.

[7]王志刚， 李振加， 曲国军， 等. 基于模糊综合评判的铰刀优化研究[J].哈尔滨理工大学学报， 2005， 10（5）： 34.

WANG Zhigang， LI Zhenjia， QU Guojun， et al. Study of Reamer Optimize with Fuzzy Comprehensive Evaluation of Reaming[J]. Journal of Harbin University of Science and Technology， 2005， 10（5）： 34.

[8]许小村， 张莉， 葛杨， 等. 胶接式气门座铰刀的开发研制[J].哈尔滨理工大学学报， 2001， 6（4）： 35.

XU Xiaocun， ZHANG Li， GE Yang， et al. Development of Bonded Carbide Valve Seat Reamer[J]. Journal of Harbin University of Science and Technology， 2001， 6（4）： 35.

[9]TOWFIGHIAN S， BEHDINAN K， PAPINI M， et al. Finite Element Modelling of Low-Speed Femur Reaming Using Reamers with Irregular Tooth Spacing[J]. Journal of Sound & Vibration，2008，318（4-5）：868.

[10]HORST B， NATALIYA L， MARKUS M， et al. Verification and Application of A New 3D Finite Element Approach to Model the Residual Stress Depth Profile after Autofrettage and Consecutive Reaming[J]. Procedia CIRP，2014，13（3）：72.

[11]YANG Changyong， HUANG Jianzhong， XU Jiuhua， et al. Investigation on Formation Mechanism of the Burrs during Abrasive Reaming Based on the Single-Particle Abrasive Micro-Cutting Behavior[J]. The International Journal of Advanced Manufacturing Technology，2021（113）：907.

[12]王大明.缸盖气门座圈切削过程仿真与优化[D].吉林：吉林大学，2011.

[13]高凯晔.基于加工仿真的钛合金Ti6Al4V螺旋铣孔专用刀具优化设计[D].浙江：浙江大学，2015.

[14]李玉平， 周里群， 吳义斌， 等. 金属二维正交切削的有限元分析与刀具角度优化[J].精密制造与自动化， 2012， 1（3）： 13.

LI Yuping， ZHOU Liqun， WU Yibin， et al. Finite Element Analysis and Tool Angle Optimization of Twodimensional Orthogonal Cutting of Metal[J]. Precise Manufacturing & Automation， 2012， 1（3）： 13.

[15]夏江， 丁文锋， 仇博， 等. 镍基高温合金高速超高速磨削成屑过程的三维仿真研究[J].金刚石与磨料磨具工程， 2020， 40（6）： 59.

XIA Jiang， DING Wenfeng， QIU Bo， et al. 3D Sim-ulation Study on the Chip Formation Process in Hig-h Speed and Ultra-high Speed Grinding of Nickel-b-ased Superalloy[J]. Diamond and Abrasives Enginee-ring， 2020， 40（6）： 59.

[16]王玉龙.灰铸铁HT250铣削加工实验与仿真研究[D].昆明：昆明理工大学，2016.

[17]岳彩旭， 郝胜宇， 黄翠， 等. 淬硬钢模具曲面铣削有限元仿真及试验研究[J].哈尔滨理工大学学报， 2018， 23（5）： 40.

YUE Caixu， HAO Shengyu， HUANG Cui， et al. 3D FEM Simulation and Experiment Research for Milling Process of Hardened Curved Mold[J]. Journal  of Harbin University of Science and Technology， 2018， 23（5）： 40.

[18]张阳.氮化硅刀具车削灰铸铁的有限元仿真分析及实验验证[D].广州：华南理工大学，2019.

[19]岳彩旭， 刘鑫， 刘智博， 等. 基于有限元仿真的拼接模具铣削用刀具优化[J].中国机械工程， 2020， 31（17）： 2085.

YUE Caixu， LIU Xin， LIU Zhibo， et al. Tool Optimization for Splicing Die Milling Processes Based on Finite Element Simulation[J]. China Mechanical Engineering， 2020， 31（17）： 2085.

[20]IMEK B， TANSEL Y， IMEK E H. A RSM-Based  Multir-Response Optimization Application for Determining Optimal Mix Proportions of Standard Ready-Mixed Concrete[J]. Arabian Journal for Science and Engineering， 2016， 41（4）： 1435.

[21]李峰， 曹一凡， 刘维伟， 等. 基于萤火虫算法的CFRP材料铣削刀具结构优化[J].宇航材料工艺， 2019， 49（1）： 21.

LI Feng， CAO Yifan， LIU Weiwei， et al. Optimization of Tool Geometric Parameters in Milling of CF-RP Based on Firefly Algorithm[J]. Aerospace Materials & Technology， 2019， 49（1）： 21.

（编辑：温泽宇）