怎样求平面直角坐标系内三角形的面积
2022-05-25曹翁云
曹翁云
在平面直角坐标系中求三角形的面积,一般要根据三角形各顶点的坐标,确定图形的边长和高,进而利用面积公式求得.但根据三角形的三边与坐标轴的位置关系不同,求解面积的方法也有所区别.下面介绍三角形的三边在平面直角坐标系中不同情况下三角形面积的求法,以供大家参考.
一、求一边在坐标轴上的三角形的面积
当三角形有一边在x轴(或y轴)上时,一般以x轴(或y轴)上的边为底边,其长等于x轴(或y轴)上两个顶点横坐标(或纵坐标)差的绝对值,这边上的高就等于另一个顶点纵坐标(或横坐标)的绝对值,然后直接利用三角形的面积公式求解.
例1如图1,三角形ABC的三个顶点的坐标分别是A(4,0),B(-2,0),C(2,4),求三角形ABC的面积.
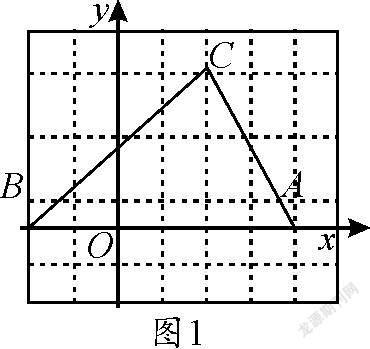
分析:要求三角形的面积,需要分别求出其底边及高.由图1可知,三角形ABC的邊AB在x轴上,容易求得AB的长,而AB边上的高,恰好是C点到x轴的距离,也就是C点的纵坐标的绝对值.
解:∵A(4,0),B(-2,0),∴AB=4-(-2)=6.
∵C(2,4),∴C点到x轴的距离,即AB边上的高为4,
点评:当三角形的两个顶点同时在x轴(或y轴)上时,求面积的关键就是求出三角形的高.这个距离就等于这个点的纵坐标(或横坐标)的绝对值.
二、求一边平行于坐标轴的三角形的面积
当三角形中有一条边与坐标轴平行时,我们解题的思路与例1相似,选择平行于坐标轴的线段作为底,这条边的长等于两个顶点横坐标(平行横轴)或纵坐标(平行纵轴)的差的绝对值;这条边上的高则等于平行于坐标轴的边与第三个点的距离.
例2如图2,已知A(-3,-2),B(3,-2),C(-2,2),求△ABC的面积.
分析:由于A、B两点的纵坐标都是-2,所以线段AB平行于x轴,因此,我们以AB为三角形的底边,过点C作CD⊥AB,垂足为D,再根据坐标的意义分别求出AB的长和AB边上的高CD的长,即可求出这个三角形的面积.
解:过点C作CD⊥AB,垂足为D,如图2.
∵A(-3,-2),B(3,-2),∴AB=3+3=6 .
又∵C(-2,2),
∴点C到AB的距离为2+2=4,即AB边上的高CD的长为4.
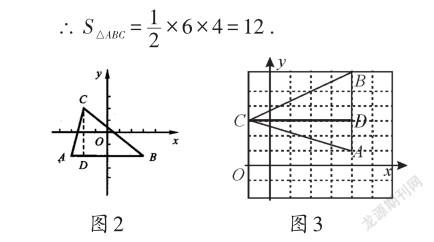
例3如图3,三角形ABC三个顶点的坐标分别为A(4,1),B(4,5),C(-1,2),求三角形ABC的面积.
分析:由A(4,1),B(4,5)两点的横坐标相同,可知边AB与y轴平行,因而易求AB的长度.作AB边上的高CD,则D点的横坐标与A点的横坐标相同,也是4,这样就可求得线段CD的长,进而可求得三角形ABC的面积.
解:∵A,B两点的横坐标相同,
∴边AB∥y轴,∴AB=5-1=4.
作AB边上的高CD,则D点的横坐标为4,
∴CD=4-(-1)=5,

点评:这两类题目都是最基础的求三角形面积问题,都可以直接利用三角形的面积公式求解.求底时一般选择位于坐标轴上或平行于坐标轴的线段,利用两点的纵坐标之差或横坐标之差得出边长,关键点在于找到底边对应的高.
三、求直角坐标系中任意三角形的面积
如果三角形三边均不平行于坐标轴,无法直接求边长和高,我们通常采用割补法.用平行于坐标轴的直线将三角形割补成“横平竖直”的基本图形,或将三角形补为长方形、直角梯形,运用求差法计算三角形的面积;或将三角形分割成几个小直角三角形,运用求和法求得原三角形的面积.
例4在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(-3,-1),B(1,3),C(2,-3),求△ABC的面积.
分析:本题所求三角形的面积不易直接计算,可运用分割法或形补法将三角形转化为其他易于求解的图形,通过求有关图形面积的和或差求得原三角形的面积.
解法1:形补法.
如图4,分别过B、C作y轴的垂线,再分别过A、C作x轴的垂线,组成矩形EFCR,
∵A(-3,-1),B(1,3),C(2,-3),
∴EH=FQ=3,EM=RN=3,FM=CN=3,RH=CQ=2,AM=1,
∴EA=3+1=4,RE=3+1=4,BR=2- 1=1,RC=3+3=6,CF=2+3=5,

点评:由于平面直角坐标系的特殊性,水平线段和竖直线段的长度比较容易计算.当所求三角形的面积不易直接计算时,就可以利用割补法得到各种基本图形的面积来进行和差计算.
