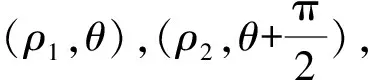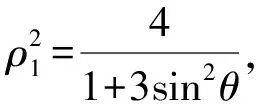数学理科试题(适用于全国卷)
2022-05-23刘海涛
刘海涛
(安徽省芜湖市第一中学 241000)
一、选择题

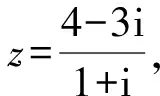
A. (-2,+∞) B. (-∞,2) C.AD.B
解题思路因为A=(-3,+∞),所以A∪B=A,故选C.
3.若函数y=(a2-2a-2)xa2-3a-4为幂函数,且图象与两坐标轴无交点,则实数m的值为( ).
A.3 B.3或1 C.3或-1 D.-1
解题思路由于函数y=(a2-2a-2)xa2-3a-4为幂函数,所以a2-2a-2=1.又幂函数图象与两坐标轴无交点,所以a2-3a-4≤0,解得a=3或a=-1,故选C.
4.为贯彻落实党中央关于党史学习教育的总体部署,今年4月,教育部在中小学部署开展了“从小学党史 永远跟党走”主题教育活动.某校开展了学党史读书活动,学生积极参加,现对该校学生每周学党史读书时间进行统计,统计结果绘制成频率分布直方图,如图1,则该校学生每周学党史读书的平均时间(单位:小时)为( ).

图1
A.11.6 B.11.20 C.11.25 D.11.30
解题思路由题意得频率之和为1,即(0.1+a+0.4+0.25+0.1)×1=1,解得a=0.15,则学党史读书时间的平均数为9.5×0.10+10.5×0.15+11.5×0.40+12.5×0.25+13.5×0.10=11.6(小时),故选A.
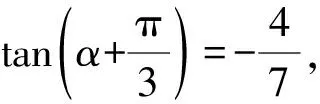
解题思路依题意,得
故选B.
6.已知函数f(x)=ln(x+2)+m的图象不经过第二象限,则m的取值范围为( ).
A.m<-ln2 B.m≤-ln2
C.m>ln2 D.m≥ln2
解题思路由对数函数的图象和性质,可知函数f(x)在(-2,+∞)单调递增,若函数图象不经过第二象限,则ln(0+2)+m≤0,解得m≤-ln2.
故选B.
7.已知等比数列{an}中,a1=1,a9=64,则a5=( ).
A.8 B.-8 C.10 D.±8
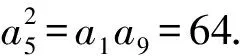
故选A.



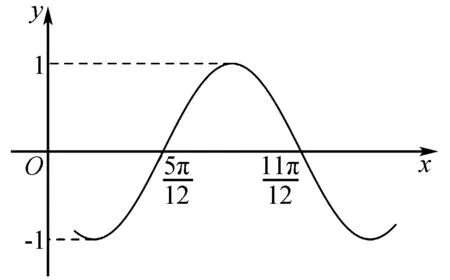
图2

A.①②④ B.②③④ C.①②⑤ D.③④⑤
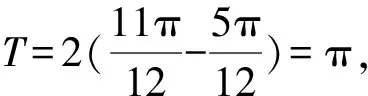




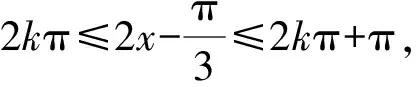
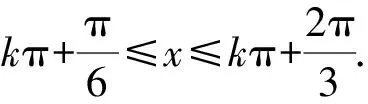

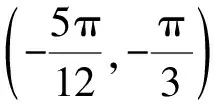
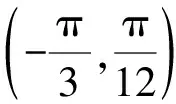



解题思路1 由题知两条渐近线方程为4x±3y=0,设P(x0,y0),则lPP1:3x+4y-3x0-4y0=0,lPP2:3x-4y-3x0+4y0=0.







故选D.
11.由0,1,2,3,4,5组成的没有重复数字的五位数,从中任意抽取一个,则其恰好为“前3个数字保持递增,后3个数字保持递减”(如五位数“12543”,前3个数字“125”保持递增,后3个数字“543”保持递减)的概率是( ).


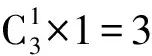
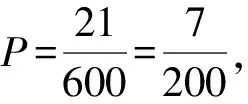
C.(-1,1) D.(-1,+∞)
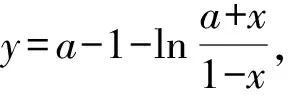
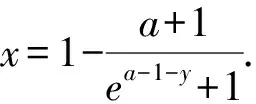
由g(x)与f(x)互为反函数,得
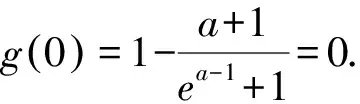
即ea-1=a,构造函数φ(x)=ex-1-x,求导得φ′(x)=ex-1-1,当x<1时φ′(x)<0,当x>1时φ′(x)>0,所以φ(x)在(-∞,1)上单调递减,在(1,+∞)上单调递增.
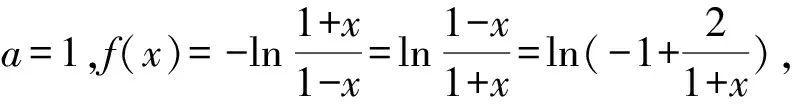
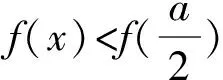
二、填空题


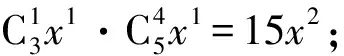

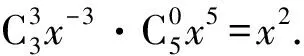
综上该展开式中含x2项的系数为46.
14.已知△ABC的内角A,B,C的对边分别为a,b,c,且b2>a2+c2,sinB=sinC.设△ABC的面积为S,若4bS=a(b2+c2-a2),则A=____.
解题思路由4bS=a(b2+c2-a2),得2abcsinB=2abccosA,即sinB=cosA.
由b2>a2+c2,得cosB<0,即B为钝角.

又sinB=sinC,所以cosA=cos2A.
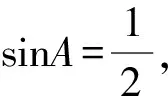
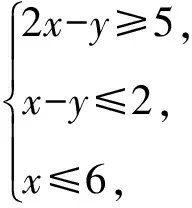

图3

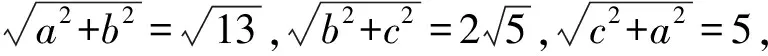
三、解答题
17.已知数列{an}的前n项和Sn满足Sn=2an-1(n∈N*).
(1)证明:数列{an}为等比数列,并求an.
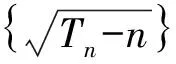
解题思路(1)当n=1时,得a1=1.当n>2时,Sn-1=2an-1-1,所以an=Sn-Sn-1=2an-2an-1.所以an=2an-1.所以{an}是以1为首项,2为公比的等比数列,所以an=2n-1.
(2)设等差数列{bn}的公差为d(d≥0),则T1=b1=2,T2=4+d,T3=6+3d.
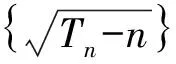
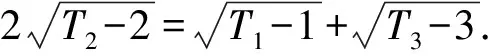
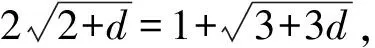
所以Tn=n2+n.
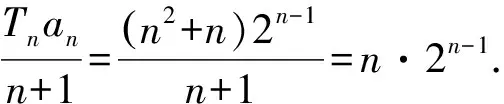
所以Wn=1·20+2·21+3·22+…+n·2n-1.
故2Wn=1·21+2·22+…+(n-1)·2n-1+n·2n.
两式相减,得
-Wn=20+21+22+…+2n-1-n·2n
=2n-1-n·2n.
所以Wn=(n-1)·2n+1.
18.新冠病毒变异株奥密克戎导致欧美多国新冠病例数激增,为全球抗疫带来新的挑战.某市防疫部门为保障该市的防疫物资质量,联合质检部分对该市甲、乙两家口罩生产企业进行检查,分别从这两家企业生产的某种同类口罩中随机抽取了100个作为样本,并以样本的一项关键质量指标值为检测依据.
已知该质量指标值对应的产品等级如下:

质量指标值[15,20)[20,25)[25,30)[30,35)[35,40)[40,45)等级次品二等品一等品二等品三等品次品
根据质量指标值的分组,统计得到了甲企业的样本频率分布表和乙企业的样本频数分布直方图(如图4,其中a>0).

质量指标值[15,20)[20,25)[25,30)[30,35)[35,40)[40,45)频数2184814162
(1)为确保口罩使用者的防疫安全性,甲企业将所有次品口罩销毁,并将一、二、三等品的售价分别定为2元、1元、0.5元.一名顾客随机购买了甲企业销售的2个口罩,记其支付费用为X元,用频率估计概率,求X的分布列和数学期望;
(2)如果你是某学校的后勤采购人员,需要为学校师生采购口罩,请你根据图表数据,自定标准,对甲、乙两企业口罩质量的优劣情况进行比较,来决定购买哪个企业生产的口罩.

随机变量X的分布列为:

X11.522.534P1361919161314
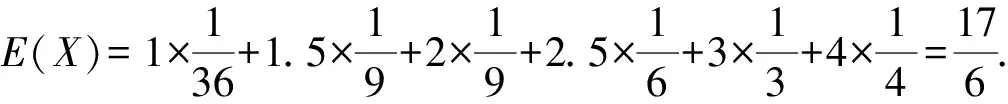
(2)答案不唯一,参考如下:
①以口罩的合格率(非次品的占有率)为标准,对甲、乙两家企业的口罩质量进行比较,由图表可知,(a+0.020+0.022+0.028+0.042+0.080)×5=1,得a=0.008,所以乙企业的样本中次品的频率为(a+0.020)×5=0.14,则合格率约为0.86,甲企业口罩的合格率约为0.96,所以甲企业口罩的合格率高于乙企业口罩的合格率,故认为甲企业的口罩生产质量更高,故采购甲企业的口罩.
②以口罩中一等品的概率为标准,对甲、乙两家企业的口罩质量进行比较,根据图表可知,甲企业口罩中一等品的概率约为0.48,乙企业口罩中一等品的概率约为0.4,即甲企业口罩中一等品的概率高于乙企业口罩中一等品的概率,所以甲企业的口罩生产质量更高,故选择采购甲企业的口罩.

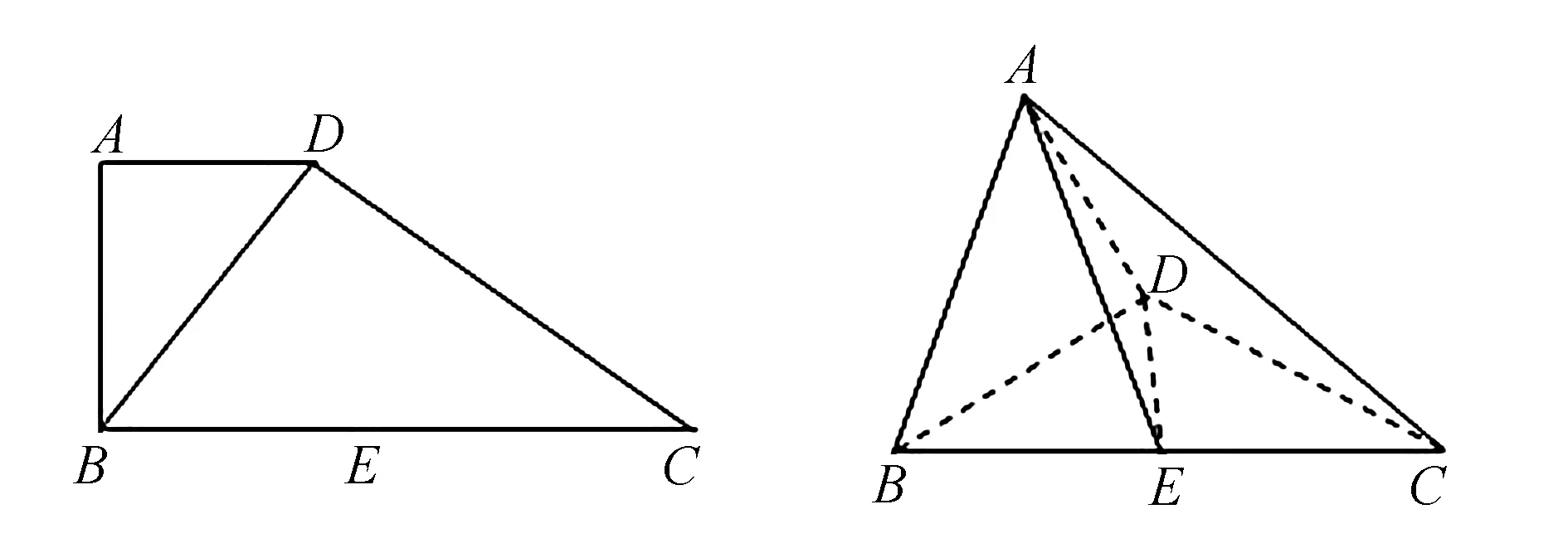
图5 图6
(1)求证:平面ABD⊥平面ADC;
(2)求直线AC与平面ADE所成角的正弦值.


图7
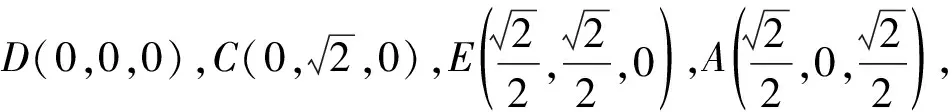



图8
(1)求椭圆Γ的离心率;
(2)若椭圆Γ的短轴长为2,直线AB与AC分别交直线l:x=a+1于E,F两点,求△AEF的面积最小时,k1+k2的值.


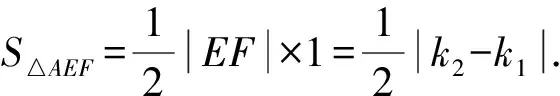
21.已知函数f(x)=e-x+sinx,g(x)=ax(a∈R).
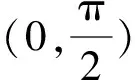
(2)若函数h(x)=f(x)-g(x)在区间(0,2π)内单调递减,求实数a的取值范围.

当x∈(0,t)时,f″(x)>0,f′(x)单调递增;

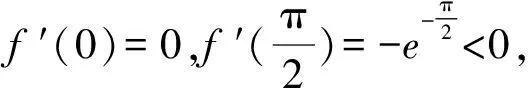
当x∈(0,x0)时,f′(x)>0,f(x)单调递增;

所以x0为f(x)的极大值点,得证.
(2)由题意可知h(x)=e-x+sinx-ax在(0,2π)上单调递减,则h′(x)=-e-x+cosx-a≤0在(0,2π)上恒成立,参变分离得a≥-e-x+cosx,x∈(0,2π),令φ(x)=-e-x+cosx,x∈(0,2π),φ′(x)=e-x-sinx,当x∈(π,2π)时,φ′(x)>0恒成立,所以φ(x)在(π,2π)上单调递增;当x∈(0,π)时,φ″(x)=-e-x-cosx单调递增,
φ″(0)=-e0-cos0=-2<0,
综上,a≥φ(2π)=1-e-2π.

(1)求曲线C1的极坐标方程;
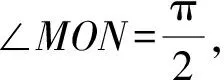
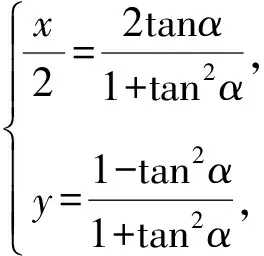
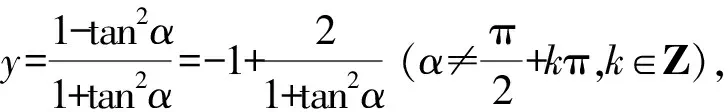
所以-1 因为y≠-1,所以曲线C1的极坐标方程为 23.已知f(x)=|2x-2|+|x+3|, (1)求不等式f(x)≤x+3的解集;