运用刚体的不形变特性 求解相关运动学问题

王伟民

(安徽省太和县宫集镇中心学校 236652)

例题1如图1所示，细棒AB水平放置在地面，A端紧挨着墙面，C为AB棒的中点.现让棒的A端沿着墙面匀速上移，当B端与C点的速度大小相等时，AB棒与水平地面的夹角为( ).

A.30° B.45° C.60 D.90°

图1 图2

分析在细棒AB按题目所给条件运动过程中，棒的两端点分别在竖直墙面和水平地面上运动，细棒与墙面和地面始终围成一个直角三角形，因为直角三角形斜边的中线等于斜边的一半，所以，棒AB的中点C到直角顶点O的距离始终等于AB长度的一半，因此，在棒AB的整个运动过程中，其中点C的运动轨迹是以O为圆心，棒长一半为半径的四分之一圆弧.我们用多种方法对该问题进行解析——

解法1——微元法

解析如图2所示，设棒长AB=L，在棒运动过程中的某一时刻，棒AB与水平地面的夹角∠ABO=θ，此后在时间元内，A端运动一段微元dL到E，与此同时，B端在水平地面运动到D，棒的中点C沿弧线运动到H.

先确定端点B速度的大小.

=dLtanθ

∴vB=vtanθ

再确定AB中点C的速度大小.

图2中，分别过E和B作EF∥OB，BF∥DE，两线相交于F，则四边形EFBD为平行四边形，∴BF=DE,∵DE=AB=L,∴BF=DE=L.

设∠HOC=dθ,则∠ABF=∠AGE=∠HDO-∠HBO=∠HOB-∠COB=dθ,

∴△OCH∽△BAF(同为等腰三角形),

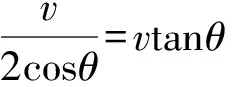
故，本题的正确选项是A.

解法2——确定瞬心法

刚体转动问题中，在刚体上取任意两点，过这两点分别作这两点在某一时刻运动方向的垂线，两垂线的交点便是该时刻刚体转动的速度瞬心.

解析如图3所示，设棒AB在运动过程中的某一时刻，它与水平地面的夹角为θ，分别过A、B作AD⊥OA，BD⊥OB，两线交于点D，则D为该时刻棒AB的瞬心，易知四边形ADBO是矩形，其对角线的交点便是AB的中点C，当B、C两点的速度相等时，有DC=DB

∴∠DBC=60°,∴θ=30°

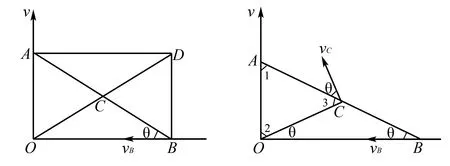
图3 图4

解法3——根据“刚体上任意两点的速度在这两点所确定直线方向上的分量相等”进行求解

由于刚体不形变，所以，刚体在运动过程中(包含平动和转动)，刚体上任何两点之间的距离保持不变，因此，刚体上任意两点在任意时刻的速度在这两点确定直线方向上的分量始终保持相等.

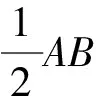
∵OC=CA=CB

∴∠COB=∠CBO=θ

∴∠2=∠3

∵∠2=∠1

∴∠1=∠2=∠3=60°

∴θ=30°

比较三种解法可以发现，后面的两种解法比较简洁.我们不妨利用第三种方法对例题1的一个变式进行求解.

例题2 如图5所示，细棒AB水平放置在地面，A端紧挨着墙面，C为AB棒的中点.现让棒的A端沿着墙面匀速上移，当C点速度大小是B端速度大小的n倍时，AB棒与水平地面的夹角是多大？(结果可以用反三角函数表示)

图5

解析由上面解法三的分析可知，在图5中α+β=90°，α=2θ.因为vB和vC在AB方向上的分量相等，所以有：

vBcosθ=vCcosβ

∵vC=nvB

∴cosθ=ncosβ

∴cosθ=nsinα

∴cosθ=nsin2θ

∴cosθ=2nsinθcosθ

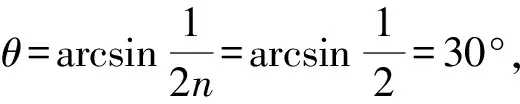
实际上，例题1给出的问题只是例题2问题的一个特例，因此，例题2对应的问题是例题1对应问题的更具一般性的推广.