基于卷积神经网络的人群突散异常行为检测

徐桂菲，王 平，罗凡波，王 伟，胡 军，宋秋霜

(1.西华大学 电气与电子信息学院，四川 成都 610039； 2.国网四川省电力公司 达州供电公司，四川 达州 635000)

0 引 言

基于智能视频监控系统可以有效检测人群异常行为，除了在运动场等特殊场景下，人群突散行为本就是一种具有隐藏危害的人群异常行为[1]，近年来随着城市人口日益增多，城市中车站、商场等场所人群密度越来越大，一旦发生人群突散行为，极大可能会发生拥挤踩踏人群事件[2]，造成极为严重的公共安全事件。传统的视频监控主要还是依靠人力时刻观察监控画面，从而实现对人群异常行为的判定，这类方法不仅耗费人力，且对于异常行为的判定具有一定的主观性。因此，采用智能视频监控[3]进行人群突散异常行为的检测具有重大意义，其能提高监控检测的时效性和准确性[4]。

目前，国内外已有不少的研究者已经在人群异常行为检测方面做了不少的研究工作。其相关工作大致可以分为3类：第一类是基于运动轨迹的分析。如Zhou等[5]通过KLT获得行人轨迹，通过建模来确定行人异常突散轨迹帧；王洪雁等[6]根据算法获得人群运动轨迹图，再使用双流卷积神经网络(TS-CNN)检测人群突散异常行为。但这类方法在杂乱拥挤的场景中不能准确地检测和定位视频事件，在雨雾天等背景复杂模糊的场景下识别精度不理想。

第二类是基于底层特征的分析，如周培培等[4]结合灰度值和光流法提取运动目标特征，使用分类器建模检测人群异常行为。马国祥等[7]通过卷积网络和光流法提取视频中行人的特征来进行突散异常判定。Li等[8]提出一种动态纹理模型来进行异常行为的检测和定位。这类方法需要根据具体场景进行建模，鲁棒性不够好，且时效性较差。

第三类则是基于深度学习的特征分析，这类方法通过神经网络[9]可以有效提取图像的特征信息，实现目标检测。如孙月驰等[10]提出一种基于卷积神经网络嵌套模型的人群异常行为检测方法。胡学敏等[11]提出一种基于深度时空卷积神经网络的人群中异常行为检测和定位的方法。但这类方法大多都是基于个体目标进行的检测和定位，缺少对整个群体异常的检测。

针对上述方法检测中时效性较差且大多都是针对个别异常行为进行检测，本文提出一种基于多尺度卷积神经网络的人群突散异常行为检测方法。该方法使用改进的多尺度卷积神经网络(MCNN)预测行人头部坐标点，再使用坐标点计算人群平均动能、人群密度、人群分布熵这3种运动状态特征值，最后再将运动状态特征值输入到差分进化粒子群优化的极限学习机(DE-PSO-ELM)中进行训练预测，最终实现人群突散异常行为的分类。本文通过使用坐标点进行运动状态特征值的计算，相较于传统方法中使用光流法来计算，很大程度上减少了计算量。最后仿真结果表明，该算法不仅减少了计算量，检测准确率也较高。

1 人群突散异常行为检测流程

本文提出的基于深度卷积神经网络的人群突散异常行为检测方法流程如图1所示，先通过改进的多尺度卷积神经网络(MCNN)训练人群计数模型，再预测提取视频图像每一帧中每一个行人个体的头部坐标点，再使用提取的坐标点计算每一帧的运动状态特征值，最后再将运动状态特征值输入到差分进化粒子群优化的极限学习机(DE-PSO-ELM)中进行训练预测，最终得到突散异常的检测结果。

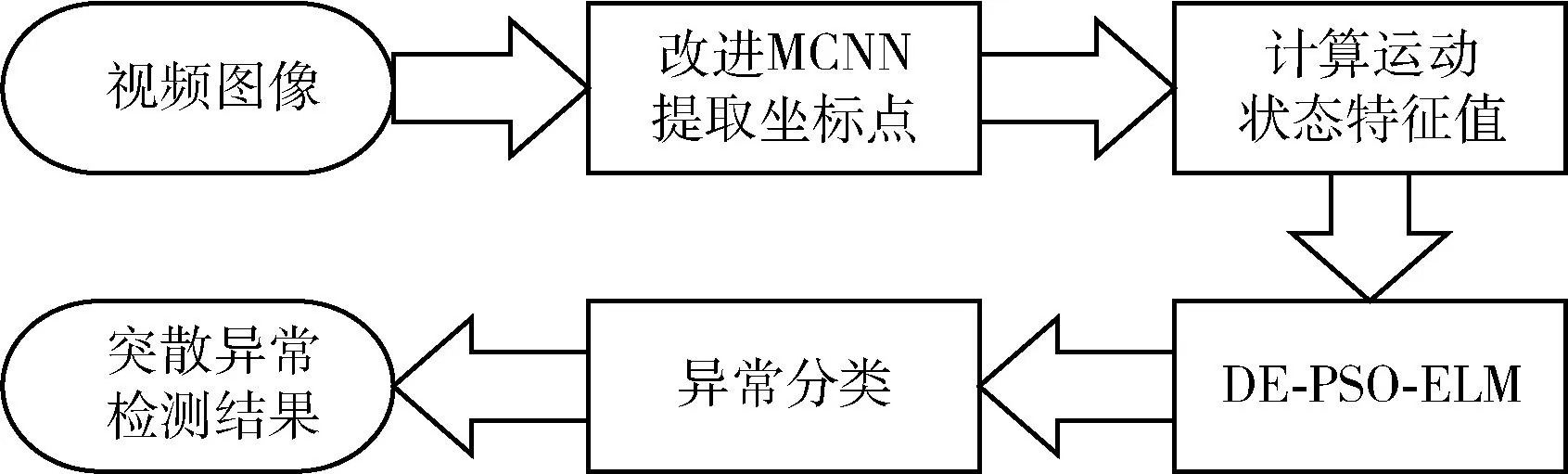
图1 人群突散异常行为检测流程

1.1 获取坐标点信息

为了减少后续工作的计算量，使用改进的MCNN人群计数网络进行人群密度图的绘制以及行人头部坐标点信息的获取。

1.1.1 人群密度图绘制

人群密度图可以更好更直观地理解人群在图中的分布情况。人群密度图绘制是通过标注行人头部，使用几何自适应高斯核来估计行人头部大小并转为密度图，然后将人群密度图输入到网络中进行训练。假设图中有一位行人头部中心坐标位置在像素点xi， 将这一点用函数表示为δ(x-xi)， 那么图中有N个行人头部中心的人群图像表示为式(1)

(1)

使用几何自适应高斯核函数Gσi(x) 生成的密度图F如式(2)所示

(2)

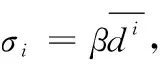
1.1.2 改进的MCNN网络结构

MCNN网络[12]即多尺度卷积神经网络，多尺度体现在使用了3列不同大小的卷积核，L列卷积核大小为 [(11×11),(9×9),(7×7)]， M列卷积核大小为[(9×9),(7×7),(5×5)]， S列卷积核大小则为[(7×7),(5×5),(3×3)]。 由于监控视频下存在透视、头部大小不一致等问题，使用多尺度卷积核可以适应不同尺度的头部大小。此外由于每一个卷积核中的值都是随机生成的，采用多核卷积的思想，在两层之间多增加一个卷积层，用来学习不同的特征。最后合并3列卷积神经网络，生成人群密度图。改进后的MCNN网络结构如图2所示。

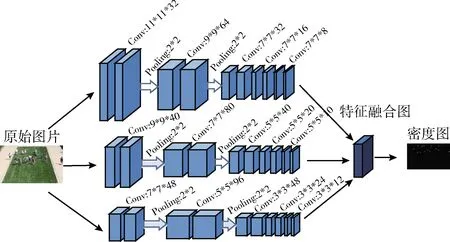
图2 改进的MCNN网络结构

损失函数定义如式(3)

(3)

其中，θ为MCNN中一个可学习的参数，Ni为训练图像的数量，Xi为输入图像，Fi为Xi的真实密度图，F(Xi;θ) 为估计密度图，L为估计密度图与真实密度图之间的损失。

根据以往人群计数网络的评价指标，我们同样采用平均绝对误差(MAE)和均方误差(MSE)作为网络的评价指标。定义如下

(4)

(5)

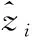
从图2可以看出，网络中使用了两层最大池化层，因此输出的密度图为输入图像的1/4大小，所以在制作训练数据的标签密度图时，也要将其制作为原图的1/4大小，几何自适应高斯核也应被限制在25个像素内。

通过改进MCNN训练以及测试，我们可以得到预测的人群密度图、每一帧的总人数以及每一个行人头部位置所对应的坐标点，为后续进行人群突散异常行为检测做准备。

1.2 突散人群运动状态特征值计算

人群行为都是处于不断运动的状态之中，本文通过动态的特征值变化去判定是否发生人群突散异常行为，定义为以下3种人群运动状态特征值。一是人群平均动能，在监控场景下，人群发生突散行为时人群平均动能会有所增大；二是人群密度值，由于监控视频下监控范围有限，当人群发生突散行为时，会出现人群离开监控视频，人群密度值就会随之减小；三是人群分布熵，发生突散行为，监控区域的人群分布会有所变化，随着突散进行，人群分布熵会随着人群分散越来越大。

1.2.1 人群平均动能

动能简单来说就是物体因运动而具有的能量，传统方法通过以前景为模板掩模来提取角点信息确定特征点，再计算特征点的运动矢量来计算人群的动能。本文的动能是指监控区域内的人群平均动能，对于每一帧图像选取图像中心点位置 (x0,y0) 作为参考点，先计算第i帧内网络预测坐标点到参考点的平均距离si， 设第i帧内一共预测出j个行人头部坐标点，该帧中的行人头部坐标点用 (xj,yj) 来表示，计算公式如式(6)，再计算第i+1帧的平均距离si+1， 再根据帧率计算其速度，从而计算人群平均动能，其计算公式如式(7)

(6)

(7)

其中，Eavg表示人群平均动能，t为单帧的时间，si为第i帧的平均距离，由于运动场景中运动对象大小相似，故m=1。

1.2.2 人群密度值

人群密度值是评判一帧中人群所占相应面积的比例大小。改进MCNN可以在生成密度图的同时，计算得出该帧的预测人数，具体得人群密度值如式(8)

(8)

式中：Ni为第i帧中预测的人群总数，λ为图像总人数修正因子，Si为第i帧图像面积，为方便计算，本文取Si=1。

1.2.3 人群分布熵

熵最开始是热力学中表征物质状态的参量之一，其物理意义是体系混乱程度的度量。1948年香农提出了信息熵的概念，对信息的多少进行了度量，体现了随机时间的不确定性。本文对人群分布计算采用信息熵的理念，来对人群分布进行说明，若人群分散，人群分布熵则会增大，反之，减小。首先将坐标进行归一化处理，使之处于 [-1,1] 之间，再将该区域平均划分为20个连续的小区域，即 [-1,-0.9)…(0.9,1]， 再计算人群分布熵，计算公式如下

(9)

其中，S(i) 为第i帧的分布熵，pj为样本在yk区间内出现的概率，count(yk) 为坐标点归一化后在yk区间的个数，k=20。

1.3 DE-PSO-ELM异常分类

极限学习机(ELM)[13]是一类基于前馈神经网络构建的机器学习方法，由Huang教授提出的单隐层前馈神经网络，具有训练参数少，学习速度快，泛化能力强的优点。在此算法中，输入层和隐含层的连接权值，隐含层的阈值都是随机设定的，且设定之后不需要再调整，输出层权重通过广义逆矩阵理论计算得出。将本文已经计算得到的3种人群运动状态特征值送入到DE-PSO-ELM中进行模型训练从而得到预测结果，由于人群运动状态值是一个动态变化的过程，最终得出的预测结果也是动态变化的。

1.3.1 差分进化粒子群算法

粒子群(PSO)优化算法[14]的基本思想是通过群体中个体之间的协作和信息共享来寻找最优解。粒子群算法通过模拟鸟群中的鸟来设计一种无质量的粒子，该粒子具有速度V和位置X两个属性，V表示粒子移动的快慢，X表示粒子移动的方向。每个粒子先在搜索空间中通过迭代方式单独搜寻个体最优解Pbest， 再将个体极值Pbest与整个群体中的其它粒子共享位置信息，寻找到整个粒子群中的全局最优解Gbest， 以此来调整自己的速度和位置。根据式(10)～式(11)更新粒子的速度和位置

Vi(t+1)=ωVi(t)+c1Rand(0,1)(Pbesti-Xi(t))+c2Rand(0,1)(Gbesti-Xi(t))

(10)

Xi(t+1)=Xi(t)+Vi(t+1)

(11)

其中，ω为惯性权重因子，t为当前迭代次数，Vi为粒子速度，Xi为粒子位置，c1,c2为加速因子，c1=c2=2，Pbest表示当前个体最优粒子的位置，Gbest表示当前群体最优粒子位置。

但粒子群优化算法容易陷入局部最优，会导致收敛精度低和不易收敛。故本文加入差分进化(DE)算法[15]进行全局优化，先计算其个体适应度，未达到最优值时，将两个随机个体向量进行变异操作，将变异向量与其父代向量进行交叉操作，再得实验向量，将实验向量与父代向量进行适应度比较，择优选择进入下一代，如此反复进行优化，最终得到全局最优解。

1.3.2 DE-PSO-ELM

本文利用DE-PSO优化ELM的输入层权值和隐含层偏置。先初始化种群，将种群随机分给PSO和DE算法，对于PSO算法，设定粒子群规模、惯性参数ω、 学习因子c1和c2、 迭代次数和最大速度等参数。计算适应度，根据最优适应度更新个体极值Pb和全局极值Gb。 对于DE优化算法，先初始化最大迭代次数Gm， 种群数Nr， 设置变异算子F、 交叉算子CR和相应的差分策略，然后对每个个体进行变异、交叉、选择操作，选择出最优个体。再将PSO选择的极值与DE选的最优个体进行种群混合重新分配执行寻优操作，最终确定最优个体值对应的输入层权重和隐含层偏置。DE-PSO-ELM算法流程如图3所示。

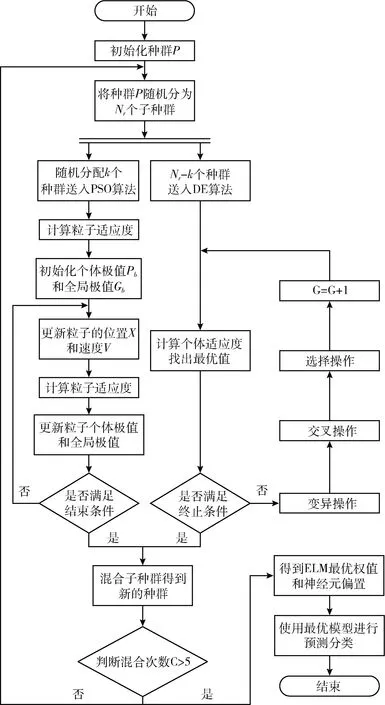
图3 DE-PSO-ELM算法流程

2 实验与结果分析

本次实验在普通PC机上进行，CPU为AMD Ryzen 5 3600，3.60 GHz，16 G内存，显卡为RTX 2070 SUPER，8 G，改进的MCNN网络是在Anaconda3+Pytorch1.3.1+cuda10.1+cudnn7.5.1+Python3.7.1环境下搭建进行训练测试的，最后人群状态特征值和异常分类是在MATLABR2020a环境下完成的。

本文使用的数据集为明尼苏达州大学创建的UMN数据库，其中每个视频起始部分都是正常行为，随后为异常行为视频序列。本文主要采用人群单方向奔跑以及人群四散的异常行为视频。

2.1 人群密度图与人群计数

改进的MCNN的训练迭代次数为2000次，其学习率设置为0.000 01，动量系数为0.9，能量为0.75，权重衰减系数为0.05。训练迭代2000次的MAE和MSE变化曲线如图4所示，横坐标表示训练次数，纵坐标为训练过程中的MAE和MSE这两个评价指标值。从图中可以看出，MAE趋于稳定在21左右，MSE区域稳定在11左右。在训练过程中，本文最佳模型MAE=10.64，MSE=19.28。

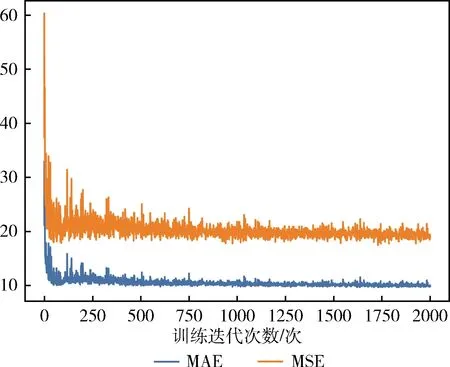
图4 训练过程网络评价指标变化曲线

将改进的MCNN网络用来预测生成视频内每帧图像的人群密度图，使用UMN数据集进行人群密度图的预测。

图5(a)、图5(d)两个图为UMN数据集中在草坪上拍摄的人群的人群异常行为视频中的两张原图，图5(a)为前期人群正常行走时候的一帧图像，图5(d)为后期人群即将要四散的图像，图5(b)、图5(e)两张图为真实的人群密度图，图5(c)、图5(f)为改进的MCNN网络预测的人群密度图。

图6(a)、图6(d)两个图为在广场上拍摄的人群异常行为视频中的两张原图，图6(a)为前期人群正常行走时候的一帧图像，图6(d)为后期人群已经四散的图像，图6(b)、图6(e)两张图为真实的人群密度图，与图6(c)、图6(f)为改进的MCNN网络预测的人群密度图。对于图6和图5的人群密度图，可以看出，图6中预测的人群密度图要优于图5中预测出来的密度，是因为图5中的行人阴影对预测有一定的影响，导致有些行人头部的预测不是很准确明显。

2.2 人群特征状态值

本文特征值计算使用的是明尼苏达大学的数据集UMN中异常人群活动的视频。本文定义了人群平均动能、人群密度值和人群分布熵3种特征状态，根据3种特征值进行无规则突散和同向突散异常的区分。

由图7(a)、图7(b)、图7(c)这个图对比可以看出，在360帧左右3种特征值都开始出现明显变化，动能和人群分布熵开始突增，人群密度逐渐减小，再对应视频中相应的帧数发现，3种状态特征值变化的拐点与视频中人群刚开始突散的时刻相对应，此时人群开始突然散开，奔跑起来，动能和分布熵逐渐增大。人群密度随着行人跑出监控区域逐渐减小。从图中可以看出人群平均动能和人群分布熵在前面正常行走的阶段也有一定的小波动，出现小波动的原因是期间有人进入或者离开监控区域，再对比图7(b)人群密度，可以看出对应帧数有人数的增减。

图8为同向突散异常行为的3个人群状态特征值的动态变化图。从图中看出，在290帧左右动能出现了明显的增大变化，再应对视频相应帧数，人群开始朝同一个方向突散，从图8(c)中可以看出分布熵的值在前期的波动较为稳定，到290帧左右，熵值开始增加，但熵值变化较小，说明人群有一定程度的分散，但分散的程度不大。相对应时刻的人群密度也开始逐渐的减小，即监控视频范围内的人群在逐渐减少，监控视频范围内的行人逐渐跑出监控之外，最终人群密度有所回升是因为后续又检测到行人进入监控区域。

2.3 DE_PSO_ELM异常分类

本文在图9及图10中对比了ELM[16,17]异常分类和基于差分进化粒子群优化的极限学习机(DE-PSO-ELM)的异常分类结果。

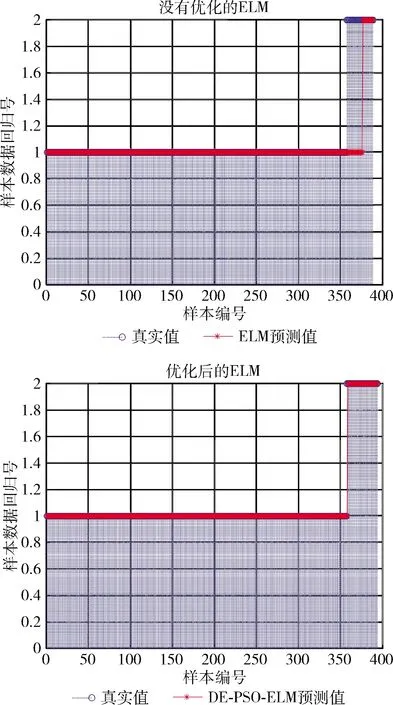
图9 无规则突散异常分类预测对比

图10 同向突散异常分类预测对比

从图9、图10中对无规则突散行为和同向突散行为的异常分类预测对比图可以看出，使用差分进化粒子群优化后的ELM对异常分类的预测要更加准确对于无规则突散的异常分类准确率达到99.75%，同向突散的异常分类准确率为99.69%，其中模型通过MAE、MAPE以及识别所用时间这3个指标进行评价。评价指标数值见表1。

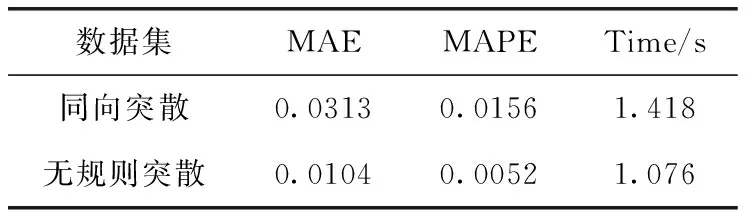
表1 模型评价值

本文通过行人头部坐标点进行人群行为的3种特征值分析，由于每一个人只会有一个坐标点，对于后续的分析计算减少了计算量，加快了计算速度，再结合MAE和MAPE值说明改进的DE-PSO-ELM模型更加适合。

以下是本文算法与文献[4]、文献[7]和文献[10]的检测准确率对比见表2。

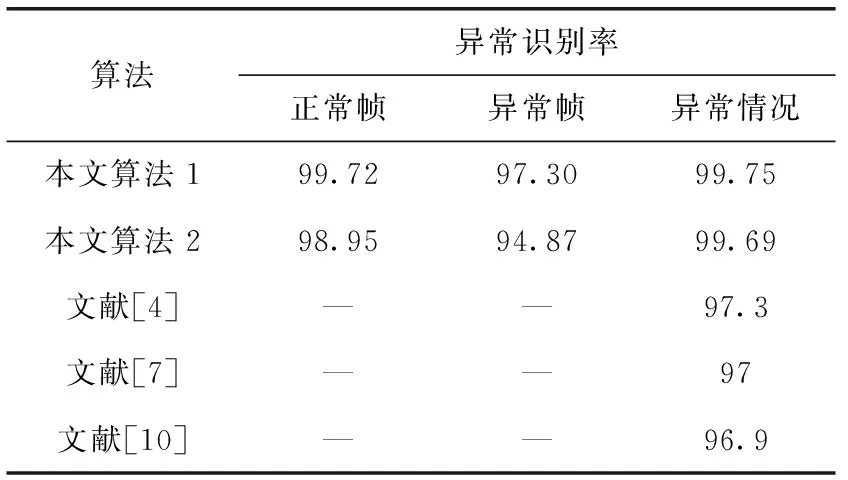
表2 检测准确率对比/%

本文算法通过改进MCNN提取行人头部坐标点，再通过坐标点计算群体间的人群平均动能、人群密度值以及人群分布熵3种动态的群体运动状态特征值，最后再将特征值送入到DE-PSO-ELM中进行异常分类，准确率达到97.69%。文献[4]和文献[7]都是通过提取外观和运动两种特征，再进行建模，最后进行异常检测分类。文献[10]通过嵌套mlpconv层改进卷积神经网络提取前景目标，再将学习到的特征输入到softmax分类器进行异常行为检测。

3 结束语

本文提出的基于深度卷积神经网络的人群突散异常行为检测方法，通过改进的MCNN提取待检测视频中行人的头部坐标点，再根据坐标点计算本文定义的3种人群运动状态特征值，减少计算量，加快运算速度。最后再将人群运动状态特征值送入DE-PSO-ELM分类模型中进行异常分类。在UMN数据集中几个场景下的实验结果表明，该方法对人群中异常突散行为检测较为准确、快速。