初中生数学建模能力测评分析与启示

孙 凯, 蔡支梅

(1.阳山实验初级中学校，江苏 苏州 215151;2.相城区漕湖学校，江苏 苏州 215000)

1 研究背景

进入21世纪以来，各国与各地区启动的新一轮课程改革都将学生数学模型思想的形成以及数学建模能力的培养作为数学教育的重要目标之一.能力通常是指一个人能够以知识性和反思性的方式解决一类困难[1].初中生数学建模能力(以下简称建模能力)是指初中学生利用形式化的数学模型去反映现实问题中的关系结构，通过对数学模型的求解和检验，解答现实原型中某些问题的能力[2].数学建模能力作为初中生(以下简称学生)最重要的数学能力之一，理应引起一线初中数学教师的重视.数学建模能力如此重要，那么学生的数学建模能力水平怎么样？学生建模能力水平的影响因素有哪些？怎样培养学生的数学建模能力？这些问题亟待研究和解决.

2 测评分析

2.1 测评对象

测评对象为某市辖内某区域全部初中学校的八年级学生，采用学业质量监测学科抽测的方式采集样本，从7 092名学生中抽测了2 389名学生，抽测比率为33.7%.抽测试题为两道典型建模试题，分别涉及“数与代数”“图形与几何”这两个领域，每题12分，根据学生的答题情况，分别赋0～12分.

2.2 测评维度

为更好地了解学生在学业质量监测中数学建模能力的具体表现，把学生在测试中表现出的数学建模能力水平划分为4个层级，并根据答题中具体的能力表现，将学生的试题得分(每题12分)相应划分为4个得分段(如表1).

表1 初中生数学建模能力水平的具体表现

2.3 试题设计

例1(“数与代数”领域)某市推广绿色家园理念，准备建立绿色无公害水果基地.现有老李、老王两家种植户，种植苹果、橙子两种果树，两家种植户种植的果树棵数与年总收入如表2：

表2 种植的有关信息

1)苹果、橙子两种果树，每棵果树的平均年收入各是多少万元？

2)若有一个种植户准备种50棵果树，为了使总收入不低于13.5万元，且苹果树、橙子树至少各种植10棵，那么该种植户所有种植方案共有多少种？该种植户最高年收入可以达多少万元？

试题说明试题是以现实生活中的果树种植为载体的应用类问题，从情境类别来看属于个人生活情境.为了符合学生的认知特点，将问题情境做适度的抽象、简化，以“文字+图表”的形式给出相关信息，使该问题有着浓厚的“现实味”和“建模味”.对学生而言，这是一道源自现实原型的建模试题，从考查内容维度看，其涉及“数与代数”领域的“方程与不等式”的内容.从考查能力维度看，主要考查学生的数学建模能力、数学运算能力.其中数学建模能力主要考查学生建构“方程与不等式”模型分析和解决问题的能力，具体的数学模型是二元一次方程组、一元一次不等式(组).试题主要考查学生从文本信息和表格信息中正确获取有用信息、抽象出数学问题、用数学符号建立“方程、不等式”模型并解决问题的能力.

例2(“图形与几何”领域)近年来，很多国家都在积极发展无人机技术，拓展无人机的行业应用.现阶段，民用无人机的用途很多，广泛应用于消防、农业、地质、气象、电力、抢险救灾等行业.

1)某次军事演习中，一架无人机停在空中对地面目标点A、点B进行侦察.已知点A，B在水平地面l上相距600 m，若要求点C处的无人机与两个目标点同时保持500 m距离(如图1)，则该无人机最高飞多高？

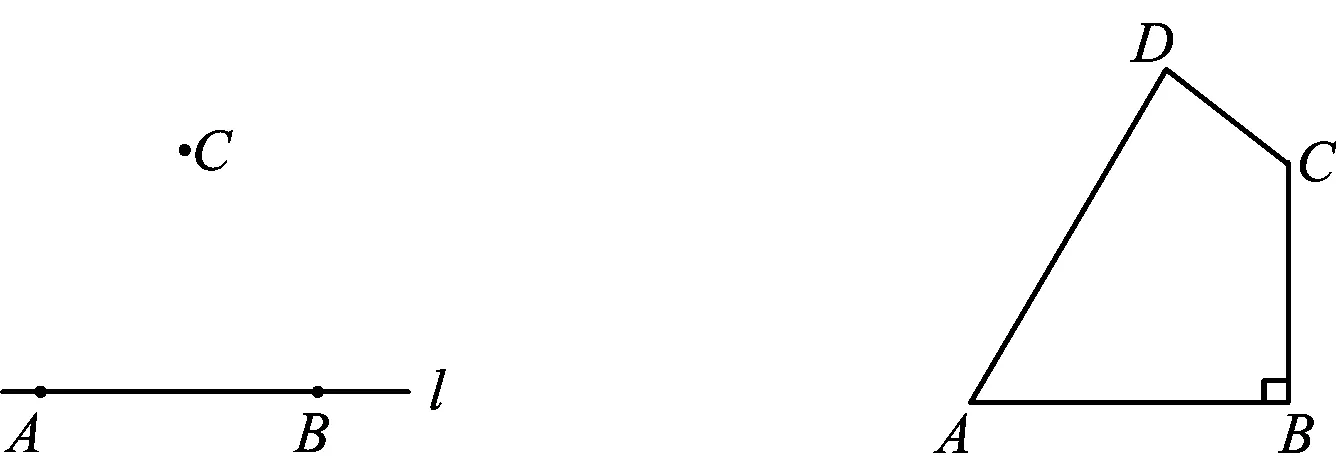
图1 图2

2)工业级无人机一般都配备了自动驾驶仪，不需要操作人员手动控制，仅需要在地面控制站上下达指令即可.比如指定航线，无人机就能按照航线自动飞行.某农业部门利用工业级无人机进行土地测绘，无人机从点A出发，沿A→B→C→D→A的顺序绕四边形地块ABCD飞了一圈(如图2)，测得AB=2 km，BC=1.5 km，CD=0.7 km，DA=2.4 km，且AB⊥BC，求地块ABCD的面积.

试题说明试题是以现实生活中的无人机为载体的应用类问题，从情境类别来看属于科学情境，以“文本+图形”的形式给出信息.从试题涉及的几何模型看，是对数学问题的一种“回译”，即将数学问题回译至现实生活，赋予数学问题现实背景及意义，将其转变成数学建模问题，使学生经历运用数学知识解决实际问题，体会数学建模的意义.从考查内容维度看，其涉及“图形与几何”领域的等腰三角形性质、勾股定理及逆定理等数学知识.从考查能力维度看，主要考查学生数学建模、逻辑推理、数学运算等能力，其中数学建模能力主要考查建构“勾股定理及逆定理”模型并解决问题的能力.

3 结果与分析

3.1 答题情况

例1从答题内容统计看，存在以下现象：很多学生不能从“文本+图表”的信息中提取有效信息，无法完成从具体情境中抽象出数学问题；不能理解具体情境中的数量关系，无法完成用数学符号系统对数学问题进行表征；不能完成或者只能部分完成方程(组)模型或不等式(组)模型的建构；数学模型求解出现错误；用数学模型求解的结果解释实际问题出现失误.从答题数据统计看，学生得分情况如图3所示，数学建模4个水平分布如图4所示.数学建模水平一占比33.2%，其中得分为0的学生高达19.8%；数学建模水平二占比20.2%，其中得5分的学生居多；数学建模水平三占比7.2%；数学建模水平四占比39.4%，其中完全正确率(满分)为总人数的20.8%.

图3

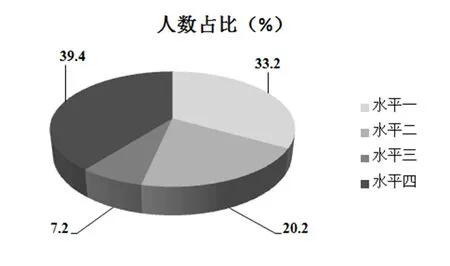
图4

例2从答题内容统计看，存在以下现象：很多学生不能从“文本+图形”信息中提取任何有效的信息，答题区域空白；将实际问题转化为数学问题时，出现理解错误；在建构数学模型求解时，模型建构不当或者对模型求解出现错误；答题不规范，答题不完整.从答题数据统计看，学生得分情况如图5所示，数学建模4个水平分布如图6所示.数学建模水平一占比25.4%，其中得0分的学生为16.9%；数学建模水平二占比19.6%，其中得4分的学生占比最多；数学建模水平三占比5.2%；数学建模水平四占比49.8%，其中完全正确(满分)的学生数为总人数的33.9%.

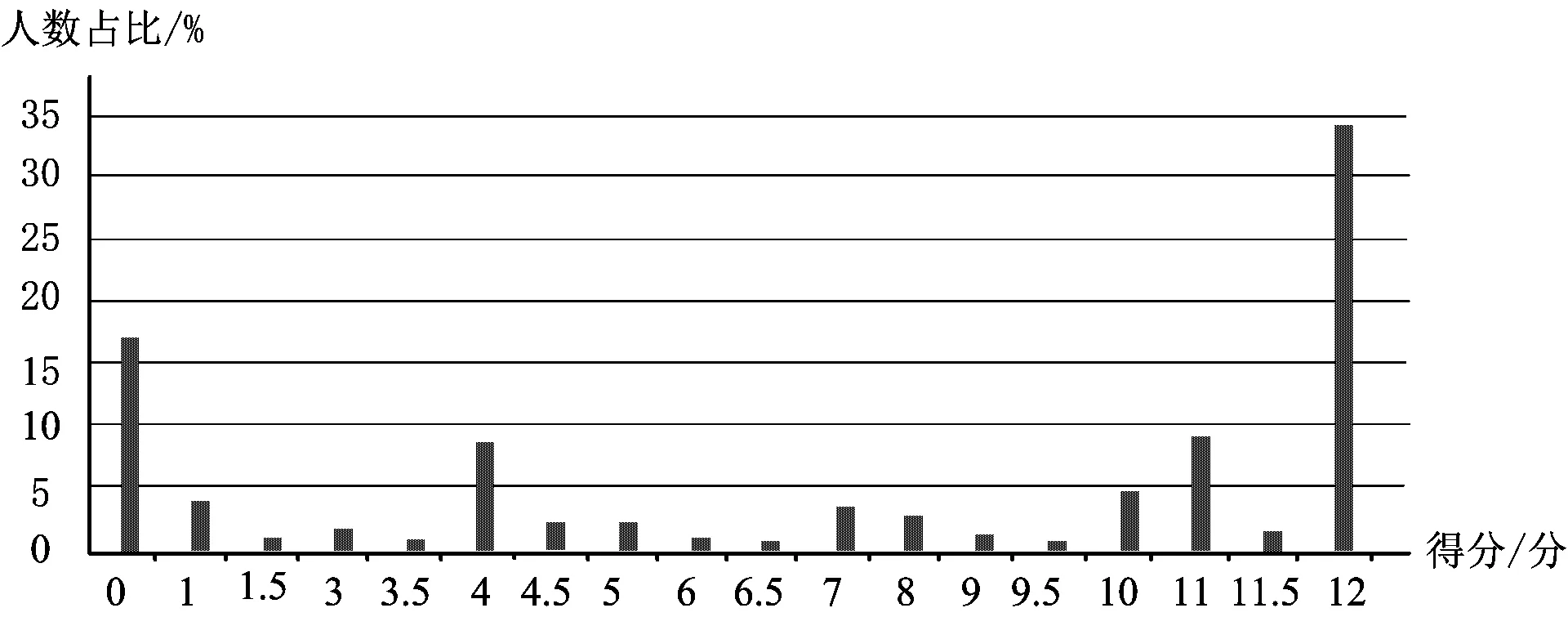
图5

图6

3.2 结果分析

数学建模能力包括：阅读理解能力、逻辑推理能力、数学化能力、计算能力和自我监控能力[4].从学生的答题情况看，存在的问题主要聚焦在阅读理解能力、数学化能力、计算能力这3个维度上.

3.2.1 阅读理解能力参差不齐

从学生答题情况看，学生的阅读理解能力参差不齐，其中大约20%的学生阅读理解能力较强，能快速、准确地获取图文信息，顺利地完成数学建模.处于数学建模能力水平一的学生中，大约19%的学生存在阅读障碍，甚至出现“密集文本信息恐惧”现象，主要表现为两种行为特征：一是心理上抵触文本信息量大的应用类问题，难以集中精力阅读理解信息甚至直接放弃阅读，导致实际问题数学化难以达成，无法完成答题；二是能认真完成阅读，只能理解和获取部分有效信息，能用数学符号表达实际问题中的部分数量关系，完成数学建模过程的某个环节.这些表现与数学建模能力水平一吻合.

比如在例1中，部分学生读不懂表2提供的信息，找不到这些数量之间的关系.又如一部分学生对“为了使总收入不低于13.5万元，且苹果树、橙子树至少各种植10棵”这句话不太理解，不知道如何进行数学表达.再如例2中“该无人机最高飞多高”的不当表述放大了学生的阅读障碍，导致约26%的学生产生了思维障碍，甚至束手无策.这些现象表明学生的数学阅读理解能力和数学表达能力有待提高.

3.2.2 数学化能力表现出较大差异

学生求解数学建模试题的首要任务是在阅读理解的基础上将实际问题数学化，即将实际问题转化为数学问题，并进行数学表达，这是能否有效建立数学模型并解决问题的关键.然而很多学生在这个环节出现错误，表现为不能将实际问题正确表达为清晰完整的数学问题，导致建构数学模型不当甚至出现错误.这些表现与数学建模能力水平二、水平三基本一致.

比如在例2第1)小题中，获得的数学问题应为“如图7，CA=CB=500 m，AB=600 m，求点C到AB的距离”.接着学生根据“等腰三角形性质”作高，建构“勾股定理”模型，计算求解即可.但有部分学生难以表达出清晰的数学问题，导致数学模型建构不当或无法完成建构.又如在例2第2)小题中，学生对△ADC的形状尚未做出判断，就直接将其看做直角三角形进行面积计算，出现模型建构失误.

图7

3.2.3 计算能力有待加强

完成数学模型建构意味着实际问题已成功地转入数学内部，对数学模型的计算求解并检验是重要环节.处于这一阶段的数学建模能力水平对应于水平四.从学生计算求解情况看，例1中出现很多的计算错误，比如方程组求解出现错解、不等式组求解出现错误、求解结果的综合判断出现错误等；例2中也出现一些面积计算上的错误现象.这些问题表明学生的数学运算能力有待加强，但仅从数学建模能力发展水平看，其水平属于较高层次.

4 思考与启示

4.1 注重数学阅读理解能力培养

数学阅读是从背景、数据等材料中获取信息的心理活动过程[5]，包含对数学语言(文字、符号、图表等)的感知和认读、新概念的同化和顺应、阅读材料的理解和记忆等各种心理活动因素[6].数学阅读理解是数学建模过程的重要组成部分，数学阅读的价值和目标在于建构数学模型解决问题.在教学中，要以教材上应用类问题为载体，加强对学生的数学阅读理解训练.这样做，一方面帮助学生克服对阅读的抵触情绪，坚定信心，踏实认真地逐字逐句完成阅读，读懂题意；另一方面帮助学生掌握阅读技巧，对文字、图表、图形等不同素材采取不同的阅读策略，弄清楚材料中的每一个关键词语、每一个数量关系，理解题目中的每一个重要信息，使学生想读、能读、会读，熟练进行文字、图形、符号这3种数学语言的转换[7]，促进数学建模能力水平尚处于水平一的学生向水平二或水平三进阶.

4.2 注重数学化能力的培养

《义务教育数学课程标准(2011年版)》明确要求学生初步形成模型思想，“通过用代数式、方程、不等式、函数等表述数量关系的过程，体会模型思想”，并且“结合实际情境，经历设计解决具体问题的方案，并加以实施的过程，体验建立模型、解决问题的过程”.初中生数学建模所面对的现实问题一般分为3类：现实原型、实际模型、数学形式.教材上的应用题和试卷上的建模试题都属于实际模型，对学生数学化能力要求并不高，学生只需建构熟悉的数学模型即可解决问题.对于实际模型类问题(应用题)，教师要将模型思想融入教学中，把常规的数学问题、数学模型放在不常规的背景下，根据问题的实际背景、数学意义对学生的求解方案进行评价[8]，有意识地引导学生经历“实际模型—数学模型—求解验证—现实结果”的问题解决过程，强化数学计算技能，提高学生综合运用数学知识解决非常规问题的能力，为学生达成数学建模能力水平四奠定基础.

4.3 注重开展真实的建模活动

教材上那些传统的文字题(应用题)，只是用现实世界的辞藻给纯数学问题加了层“外衣”，在这种情况下，所谓的数学建模只是“去掉外衣”(自然语言翻译成数学语言)，适合问题解决的数学模型就在手边[9].从两道试题的内容及设置的问题来看，例1和例2尚属于一般的数学问题解决，不同于真正的数学建模问题.在初中阶段的数学学习中，开展数学建模活动是培养学生数学建模能力的有效途径.为解决实际模型类问题在培养学生数学化能力上的欠缺，我们建议以现实世界的问题解决为抓手，每学期开展1～2次适合初中生的综合实践活动或数学建模主题活动，在完整的数学建模活动中促进学生形成模型思想，提高数学建模能力.比如开展“出租车收费问题”主题活动，自由组建数学建模团队，经历问题分析、调查、数据收集、提出假设、构建模型、模型计算、分析结果、模型验证、模型改进等数学建模过程，在以实际问题解决为指向的数学建模活动中培养学生的数学建模能力.