过程酝酿函数味道
——“锐角三角函数”的教学设计及反思
2022-05-23蔡友山
蔡友山
(宁波市第七中学,浙江 宁波 315000)
近期,在围绕“数学概念教学”这个主题进行研讨时,笔者有幸执教了浙教版《数学》九年级下册第1.1节“锐角三角函数”,由于课前和组内同行对本课进行了充分的研究和思考,课后受到与会教师的一致好评.现将本课的教学研究、教学过程及课后反思整理如下,与各位同行交流.
1 课前研讨
笔者从理解数学、理解学生、理解教学这3个维度着重思考了以下3个问题:
1)相对其他函数,锐角三角函数有何特殊性?本节课教学的重点应放在何处?
2)学生现有基础如何?他们对锐角三角函数概念的理解难在哪里?
3)教师对锐角三角函数概念的教学存在哪些误区?应如何实施锐角三角函数的概念教学?如何突破教学难点?
锐角三角函数虽然是基本初等函数,但其相对于一次函数、二次函数和反比例函数又有其自身的特殊性,这种特殊性主要体现在以下3个方面:1)对应关系的特殊性.锐角三角函数是以锐角为自变量,该角所在直角三角形的两边之比为因变量的函数.2)书写形式的特殊性.与学生此前认识的函数存在巨大反差.3)在学习弧度制之前,用角度制表示的锐角与它所在的直角三角形的两边之比并不是严格意义上的“实数”与“实数”的对应关系.单从初中阶段对函数的定义来理解锐角三角函数概念确有一定困难.这种形式与内涵的双重特殊性使其“函数”特征十分隐蔽,增加了学生理解的难度.而在实际教学中,有些教师不太重视锐角三角函数概念的形成过程,从而导致许多学生课后根本不清楚为何把它也称为“函数”.如何组织教学?本节课是一节概念课,其核心是让学生经历概念的形成过程和运用过程,在过程中让学生感悟锐角三角函数,深化对概念的理解和能力的培养.基于此,我们要突破以下4点:一是让学生发现这种边角对应关系具有“函数”的基本特征,帮助学生理解这种边角对应关系为什么是函数关系;二是引导学生对这种函数关系进行表达;三是利用题组巩固概念;四是引导学生利用定义尝试探索其性质.
2 教学设计
2.1 “锐角三角函数”概念的形成过程
环节1创设情境,引入概念.
播放滑雪影片,从中抽象出一个角,针对此情境连续设问:

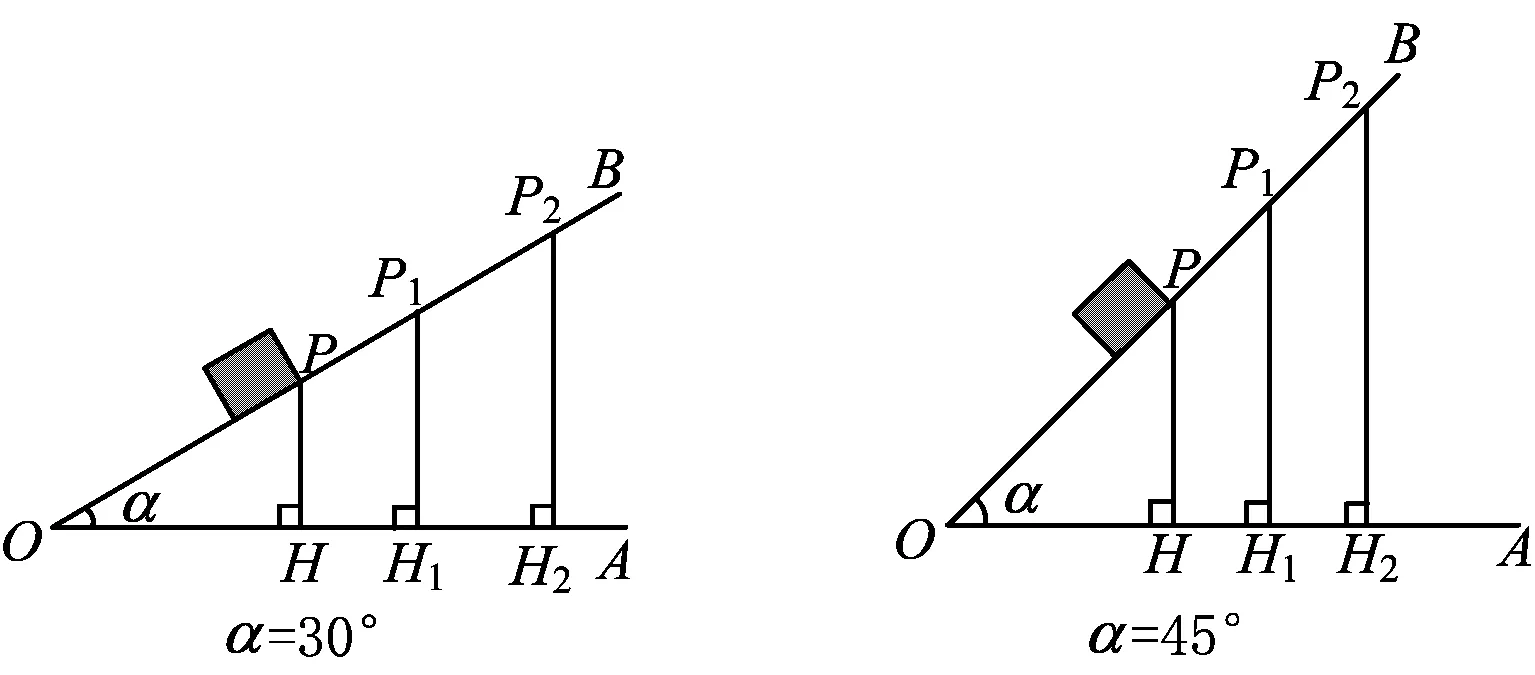
图1 图2



图3 图4

教学说明通过以上4个问题可引导学生发现:

环节2提炼本质,归纳概念.
1)纵向观察表1中的信息,你发现了什么规律?
2)横向观察表1中的信息,你又能发现什么规律?

表1 直角三角形中锐角α及的值

4)如果是函数关系,那么谁是自变量?谁是谁的函数?如何表达这种函数关系?

环节3横向比较,精致概念.
1)畅所欲言:锐角三角函数相对我们前面学习的一次函数、二次函数和反比例函数有其自身的特殊性,这种特殊性主要体现在哪里?
2)教师介绍:到了高中阶段,当锐角扩展到任意角、弧度制取代角度制时,三角函数是在平面直角坐标系中进行定义的.
教学说明通过“畅所欲言”引导学生横向比较不同类型的4种函数,让学生感悟锐角三角函数所表示的是直角三角形的边角关系,正是这种边角关系让我们今后解决直角三角形问题更方便、灵活.
通过“教师介绍”让学生了解三角函数知识的延续性和发展性,激励学生为今后高中阶段学习三角函数打下坚实的基础.
2.2 “锐角三角函数”概念的巩固过程
利用3个例题巩固“锐角三角函数”概念:
例1如图5,在Rt△ABC中,∠C=90°,若AB=10,BC=6.求∠A和∠B的正弦、余弦和正切的值.
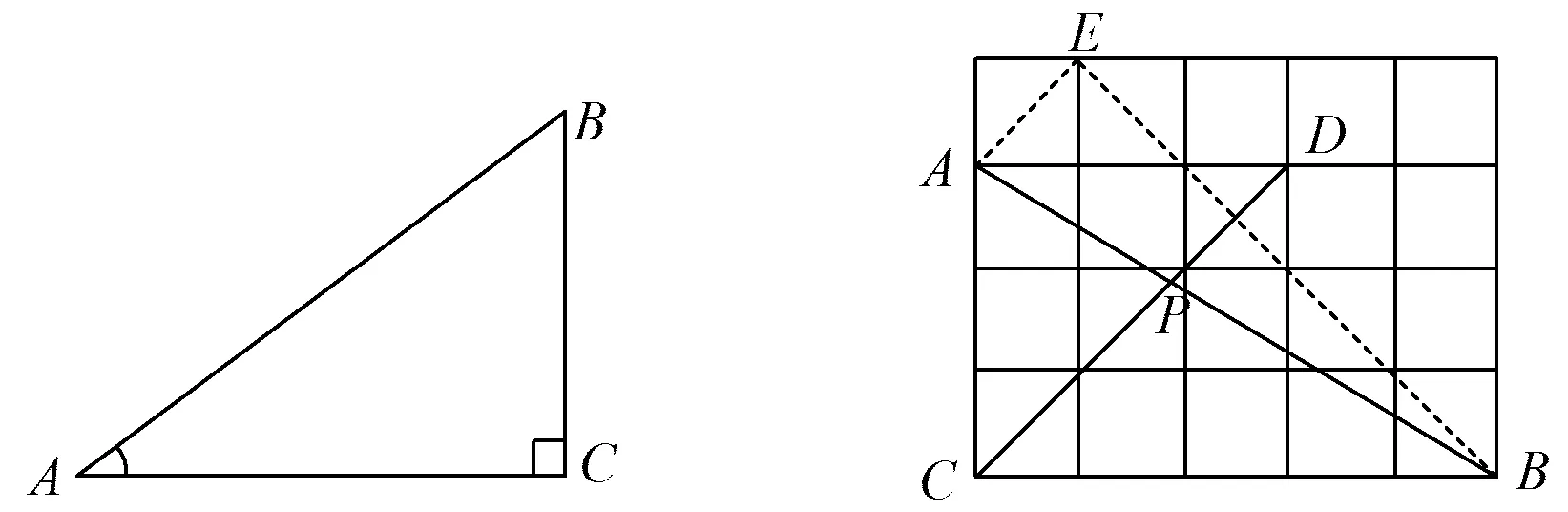
图5 图6
例2如图6,在5×4的网格中,线段AB,CD相交于点P(点A,B,C,D,E均为小正方形的顶点),则tan∠DPB的值等于
( )
A.2 B.3 C.4 D.5
例3如图7,请在6×6的网格中画出正切值等于3的锐角α(要求:用3种不同的方法,且顶点都在格点上,标出锐角α).

图7
教学说明通过以上3个例题引导学生分别从定量计算、网格求值和网格作图3个不同的角度巩固锐角三角函数的概念,培养学生分析问题和解决问题的能力.
2.3 “锐角三角函数”性质的探究过程
出示以下2个例题,让学生展开探讨:
例4如图8,在Rt△ABC中,∠C=90°,若BC=a,AC=b,AB=c.利用锐角三角函数定义探究以下问题:

图8 图9
1)∠A和∠B的三角函数值之间有什么特殊关系?
2)对于任意一个锐角α,请求出sinα与cosα的取值范围;
3)对于任意一个锐角α,你能发现sinα,cosα与tanα之间的关系吗?
4)对于任意一个锐角α,请计算sin2α+cos2α的值.
例5如图9,将一根木棒绕着点O从OA1位置顺时针旋转到OA2,OA3位置.请思考以下几个问题:
1)随着锐角α的增大,∠α的对边和邻边在做怎样的变化?
2)结合图9,探索锐角三角函数的增减性(填“增大”或“减小”或“不变”):
正弦值随锐角α的增大而______;余弦值随锐角α的增大而______;正切值随锐角α的增大而______.
3)利用第2)小题中探索的结论比较大小(填“﹥”或“﹤”或“=”):
sin 23°______sin 65°, cos 76°______cos 43°,
tan 53°______tan 78°.
教学说明通过以上问题引导学生利用锐角三角函数的定义从定性的角度探索锐角三角函数的如下性质:
1)若∠A+∠B=90°,则sinA=cosB,cosA=sinB;
2)0 4)正弦值随锐角α的增大而增大,余弦值随锐角α的增大而减小,正切值随锐角α的增大而增大. 引导学生从知识和思想方法角度回顾本节课的收获,教师从函数的发展和演变方面对知识进行提升,激发学生继续学习函数知识的欲望,课堂在学生的畅想和掌声中结束. 锐角三角函数反映的是一个直角三角形的锐角与两边之比的对应关系,正是这种特殊的边角关系使得我们今后解决直角三角形问题更方便、更灵活.同时,也为高中阶段学习任意角的三角函数知识打下了坚实基础.本节课着眼于培养学生分析、抽象、概括等能力,注重概念的形成过程,突出锐角三角函数概念的本质,在过程中酝酿“函数”味道,这种函数味主要体现在以下两个方面: 概念教学的核心就是“概括”,即以若干典型事例为载体,引导学生分析各事例的属性,抽象概括其共同本质属性,从而归纳获得数学概念[1].章建跃博士在数学核心素养的解读中强调:从数学知识发生发展过程的合理性、学生思维过程的合理性上加强思考,这是落实数学学科核心素养的关键点.要把如何抽象数学对象、如何发现和提出数学问题作为教学的关键任务[2]. 鉴于锐角三角函数概念在形式和内涵上的双重特殊性和其“函数”特征的隐蔽性,教师分两步实施其概念教学:一是通过对含30°、45°、50°这些特殊角的直角三角形的边角关系进行研究,并引导学生观察发现“在直角三角形中,一个锐角所对的直角边与斜边之比是随锐角的大小变化而变化的,当锐角的大小一定时,这个比值也随之唯一确定.”这突显的“函数”特征十分自然地唤醒学生大脑中沉睡的记忆——函数.至此,学生顿悟这种边角关系就是他们熟悉的函数关系.二是引导学生对这种函数关系进行表达.具体分3步实施:尝试表达、规范定义、类比推广.在学生认识到直角三角形的边角关系存在函数关系后,教师并没有急于告诉学生该如何表达这种函数关系,而是让学生自己尝试着表达,在学生渴望表达而又力不从心时,教师适时给出规范的定义和表达.锐角三角函数包括正弦、余弦和正切等多种表达形式,在教学时,教师选择正弦做重点突破,再类比给出其他函数形式.通过本环节教学,锐角三角函数概念已悄无声息地植入学生头脑. 利用定义和图像探索性质是研习函数的必经之路.所谓探索重在“探”的过程,即学生在问题的引导下,自主研究,归纳总结,发现其变化规律,挖掘其内在本质.荷兰数学教育家弗赖登塔尔指出:学习数学的方法是实行“再创造”,也就是由学生本人把要学的东西自己去发现或创造出来,教师的任务是引导和帮助学生去实现这种再创造,而不是把现成的知识灌输给学生[3].基于此理念,本节课在整合教材时增加了探索性质这一环节,并在此环节安排了两个例题:其中例4让学生利用定义从定性的角度探索任意锐角的三角函数值之间的关系,其目的是让学生自主发现互余的两个锐角的三角函数值之间的关系,理解同一个锐角的三角函数值之间存在着内在必然的联系;例5是从动态角度探索锐角三角函数的增减性,让学生自主发现锐角三角函数值的大小随角的大小变化并不是表面现象,有其内在的规律.由此可见,选择这些问题作为探究素材,完全符合学生的现有基础和认知规律,这一探索过程也使得本节课的“函数”味道更浓.2.4 回顾盘点,画龙点睛
3 教学反思
3.1 注重概念的形成过程,揭示函数的本质特征
3.2 注重性质的探索过程,再现函数研究路径
