对《电路理论教程》及相关文献中问题的讨论
2022-05-23吉培荣
吉培荣
(三峡大学 电气与新能源学院, 宜昌 443002)
在陈希有教授主编的《电路理论教程(第1版)》(简称为《教程(1版)》)里,作者在前言中总结该教程的特色为:①加强电路理论的电磁学基础,……;④强调概念的重要性,……[1]。不过,笔者细读《教程(1版)》后却发现了一些概念性问题。在高等学校电路和信号系统教学与教材研究会第十、十一届年会(2016年8月,兰州;2018年8月,常州)上,笔者发表了“电路理论教程中的若干问题商榷”“电路理论教程及相关文献中的若干问题商榷”两篇论文,指出了《教程(1版)》和相关文献“由卷积想到的计量单位及相关物理概念”(简称为“概念”)一文中存在有多处问题[2]。陈希有教授参加了这两次会议,并就相关问题与笔者有过多次面对面交流。从交流情况看,笔者的有些观点能够得到认可,但有些观点被认为没有道理。
目前《电路理论教程(第2版)》(简称为《教程(2版)》)已出版,可以看到《教程(1版)》中的一些问题已按笔者观点得到了改正,但有些问题依然存在[3]。本文对《教程(2版)》中依然存在的问题进行分析,这些问题也存在于“概念”中。
需要说明,在“概念”中,单位阶跃响应也称为单位阶跃特性,用d(t)表示;单位冲激响应也称为单位冲激特性,用h(t)表示。在《教程(1、2版)》中,单位阶跃响应s(t)称为单位阶跃特性,单位冲激响应h(t)称为单位冲激特性。
1 问题1及分析
1.1 问题1及笔者观点
问题1:定义式中的δ(t)单位为1/s=s-1。
笔者观点:δ(t)的定义式是纯数学式,其中的δ(t)无单位,t也无单位。δ(t)与物理量发生联系时,δ(t)本身是数值无单位,但自变量t有单位。
1.2 对问题1的分析
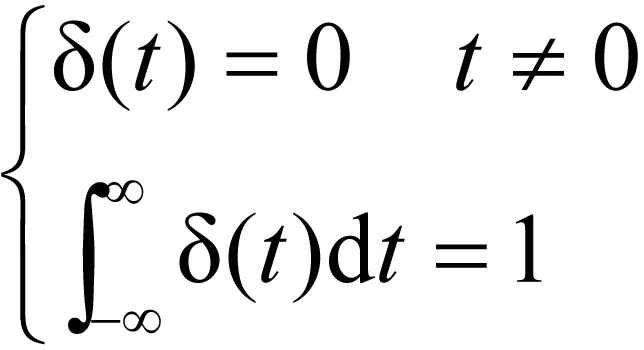
由定义可知,δ(t)本身具有时间倒数的量纲,单位为1/s=s-1。“概念”中有类似表述。
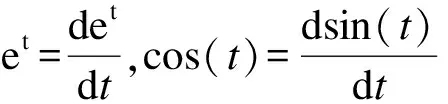
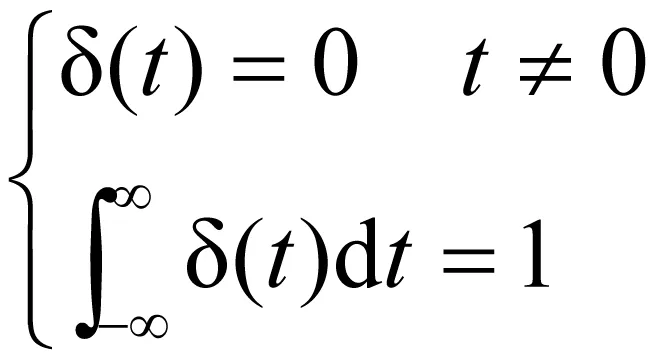
不过,单位冲激函数与物理量发生联系时,其自变量有单位,所表达的物理量也有单位,但冲激函数本身并无单位。例如,设某一电流为i(t)=δ(t)A,这里i(t)、t均是物理量,既有数值又有单位,i(t)的单位为A,t的单位为s,但δ(t)仅为数值而无单位。再如,单位直流信号的傅立叶变换对为
1(-∞ 式中单位冲激函数δ(ω)的自变量ω具有角频率的单位[4-6]。 问题2:单位冲激响应的单位等于相应单位阶跃响应的单位比上时间的单位。 笔者观点:单位冲激响应的单位与相应单位阶跃响应的单位相同。 问题3:单位阶跃响应s(t)的单位既不是电流的单位,也不是电压的单位,有四种情况:电流比(无量纲)、V/A=Ω、A/V=S、电压比(无量纲)。 笔者观点:单位阶跃响应s(t)的单位为电压的单位或电流的单位,有二种情况:A或V。 《教程(2版)》321页中有:单位阶跃特性s(t)是阶跃响应电压或电流除以阶跃电源的幅值,不再具有电压和电流的量纲,例如,无量纲或具有电导的量纲。 文献[8]中有如下论述:对单一激励的线性、时不变电路,指定响应对激励之比定义为网络函数,记为H,即 激励可以是电压源电压或电流源电流,响应可以是任一支路的电压或电流。对电阻电路,H为一实数。例如,对单个电阻R,若以外施电流作为激励,其两端出现的电压作为响应,则H=R(单位:Ω)为一实数。 按“概念”中所说幅值包括数值和单位,则有 这时的阶跃响应s(t)实为网络函数H,这显然有问题。由此也可说明幅值包括数值和单位的观点不对。 当“幅值”对应为“幅度的数值”而不包括单位时,单位阶跃响应s(t)的单位与阶跃响应的单位就是一致的,为电压或电流的单位。许多文献中的观点均如此[4-11]。 问题4:单位冲激响应h(t)的单位既不是电流的单位,也不是电压的单位,有四种情况:A/C=1/s、V/C=Ω/s、A/Wb=S/s、V/Wb=1/s。 笔者观点:单位冲激响应h(t)的单位为电压的单位或电流的单位,有二种情况:A或V。 《教程(2版)》327页中有:可以用电源的冲激强度去除冲激响应,得到规范化的冲激响应,称为单位冲激特性,用h(t)表示;如果激励是冲激电流源,冲激强度是库仑(C),响应是电压,单位是伏(V),h(t)的单位就是V/C=Ω/s。《教程(2版)》331页中有:h(t)的单位为s-1。 本文对文献[1~3]中存在的一些问题进行了分析,这些问题也部分存在于陈希有教授以前主编或参编的文献中[13-14]。相关分析是否存在不妥之处?还敬请同行学者们批评指正。 本文的讨论不仅有利于澄清相关概念,对“电路理论”课程的教学也有积极作用。2 问题2及分析
2.1 问题2及笔者观点
2.2 对问题2的分析
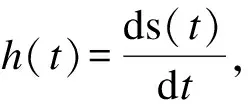
3 问题3及分析
3.1 问题3及笔者观点
3.2 对问题3的分析
4 问题4及分析
4.1 问题4及笔者观点
4.2 对问题4的分析

5 结语
