钢板梁桥腹板间隙变形及力学特征

2022-05-20吉伯海高玉强傅中秋

华东交通大学学报 2022年2期

姚悦，吉伯海，高玉强，傅中秋

（河海大学土木与交通学院，江苏南京 210098）

钢桥具有自重轻、强度高、抗震性能好、施工快捷方便等特点，近年来我国正在推广钢结构桥梁的建设，并建议70 m 以下跨径时宜采用组合钢板梁桥的结构形式。以钢板梁作为主梁结构形式的中小跨径钢桥将成为我国钢桥的主梁桥型之一[1-2]。

钢板梁桥上部主要结构包括主梁、横向联结系、纵向联结系和桥面板[3-4]。由于其构造复杂且数量较多，各构件之间约束作用明显，在车辆荷载的作用下，单个构件的变形会引起其他构造的次应力，导致疲劳裂纹的出现，影响桥梁的运营安全[5-7]。国外经过长期的钢桥运营养护发现，加劲肋与翼缘连接部位存在较大的约束与残余应力，应力水平较大。因此，后期规范要求加劲肋在腹板上截止，从而在主梁腹板上下两端形成了一段间隙，一般称之为“腹板间隙”，该位置由于较小的局部刚度以及较大的面外变形，是钢板梁桥出现疲劳裂纹最多的细节[8-12]。针对钢板梁桥腹板间隙部位的疲劳研究，早期学者主要从宏观变形角度，考虑主梁之间的相对竖向位移差，将其等效为腹板间隙上的转角作用[13]。然而，前期研究显示，腹板间隙会受到横向联结系导致的向内、向下的变形作用，从而在腹板间隙端部产生一定位移。若仅考虑宏观变形上的转角作用，在计算腹板间隙的弯矩及应力时，可能导致一定误差。此外，由于转角与位移之间存在应力耦合的关系，在一定程度上也会增加评估的难度。有必要进一步明确腹板间隙的变形特征，考虑转角与位移共同作用下，腹板间隙的应力特征，从而提高该细节疲劳评估精度。此外，基于腹板间隙构造长度较短、厚度较大的特点，考虑其弯曲切应力作用可能相对显著，对腹板间隙的正应力剪应力作用特征进行了进一步分析。

本文建立了钢板梁桥全桥有限元模型，考虑了不同主梁结构形式，明确了腹板间隙的局部变形特征，提出了转角与位移共同作用下的梁段计算模型，并通过实桥应力测试数据与有限元计算结果验证其正确性。基于该模型，进一步对腹板间隙端部的正应力与剪应力作用进行计算分析，明确其正应力与剪应力的作用比例特征，从而在腹板间隙端部焊缝的疲劳评估中，可以通过正应力及应力比例关系进行抗疲劳设计及损伤评估，无需获取剪应力或主应力，简化了细节的评估过程。

1 钢板梁桥有限元模型

1.1 有限元模型

以交通部2019 年发布的《钢板组合梁桥通用图》中4×35 m 的双主梁四跨连续组合钢板梁桥为研究对象，采用ABAQUS 有限元软件建立有限元模型[14]。主梁采用工字梁双主梁，为了方便计算，暂不考虑钢板梁的变截面特性，工字梁沿全桥纵向截面参数一致，上翼缘厚32 mm，宽度800 mm，腹板厚度20 mm，高度1 666 mm，下翼缘厚度50 mm，宽度960 mm，横桥向上双主梁之间间距为6 760 mm。

钢主梁选取Q345qD 钢材，密度为7.85 g/cm3,弹性模量E=2.1×105MPa，泊松比v=0.3。桥面板为钢筋混凝土桥面板，为方便有限元模型建立，将其简化为各向同性的材料，密度为0.25 g/cm3，弹性模量选取钢筋混凝土等效值E=3.55×104MPa，泊松比v=0.2。不考虑钢主梁与桥面板之间的相对滑移。在全局模型采用实体模型，C3D8R 单元进行划分，桥面板网格尺寸为100 mm，钢主梁网格尺寸为50 mm。

当对主梁位移及受力特征进行分析时，选取纵向桥第二跨靠近中支座第二个带有横向联结系、长度1 m 范围内的主梁段作为子模型进行精细计算。提取全桥模型中的结果作为边界条件，保留所有桥面板表面应力作为子模型的边界与荷载条件，同时为保持子模型梁体在全桥竖向位移上的相应，对下翼缘底部及四周进行约束。将主梁上翼缘与腹板设置自由端，以反映主梁腹板上更细致的变形特征。对子模型的网格进行细化，桥面板网格尺寸为50 mm，为反应焊缝应力特征，焊缝长度方向上网格尺寸设置为10 mm，焊趾部位及腹板间隙段网格尺寸为2 mm，有限元模型及尺寸如图1 所示。

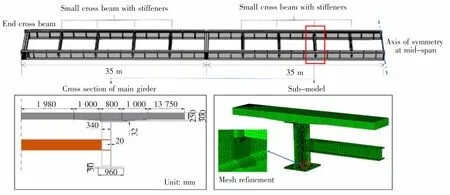
图1 有限元模型Fig.1 Finite element model

1.2 荷载模型

考虑连续梁桥中主梁自重对结构内力特征的影响，设置主梁自重作为初始荷载。同时，在桥面板上施加疲劳车荷载，分析腹板间隙的疲劳受力特征。荷载模型采用《公路钢结构桥梁设计规范》（JTG D64-2015）中的疲劳荷载模型Ⅲ，桥面板上设置10 cm 铺装层，并考虑其对荷载的应力扩散作用，单个荷载面尺寸为800 mm×400 mm，荷载集度为0.1 875 MPa[15]。

车辆荷载位置会对结构的约束及受力特征产生影响，为此考虑了不同的荷载纵横向位置进行计算。纵桥向上，车辆荷载自端支座外部向中间支座纵向每500 mm 移动并计算一次。考虑到桥梁纵向四跨内的对称性，仅对荷载位于第一跨与第二跨时进行计算，荷载纵向位置变化如图2 （a）所示。横桥向上，以主梁中心为横向荷载中心位置，根据桥梁的设计图纸，当荷载横向位置为1 200 mm时，车辆恰好位于行车道中部，为关键荷载分布位置，并以此进行第二节的计算。同时，后续为了明确横向荷载位置对结构力学特征的影响，计算横向荷载位置在0～4 400 mm 的主梁应力，横向位置移动梯度为400 mm，荷载横向位置变化如图2（b）所示[16]。

图2 荷载位置（单位：mm）Fig.2 Load position(Unit:mm)

1.3 主梁结构形式

钢板梁桥结构形式多样，其中最明显的差异是横向联结系的结构形式，目前我国主要采用的是以工字梁作为小横梁的形式。考虑到结构形式导致的构件之间约束差异，建立了不同主梁结构，包括X型横向联结系、大横梁与小横梁，其中小横梁考虑了单个加劲肋与成对加劲肋的结构形式，如图3 所示[17-18]，以分析腹板间隙局部的位移变化。

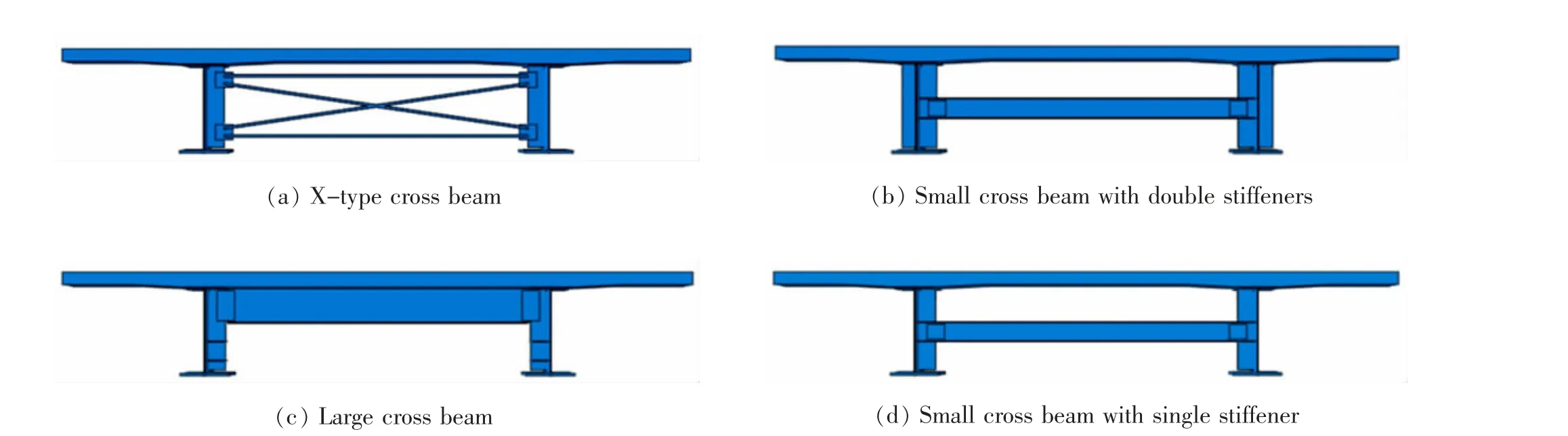
图3 主梁结构形式Fig.3 Main girder structure

2 腹板间隙变形特征分析

为了明确腹板间隙的变形特征，选取腹板间隙上端、腹板间隙下端与加劲肋端部3 个位置，分析其在车辆荷载作用下的位移变化进行判断，如图4所示。计算横向荷载位置为1 200 mm 时，各点在水平方向与竖直方向的位移变化。当腹板间隙上端与下端存在水平位移差时，则腹板间隙梁段截面存在位移变形。当腹板间隙上端与加劲肋端部存在竖向位移差时，则腹板间隙上端存在转角作用。

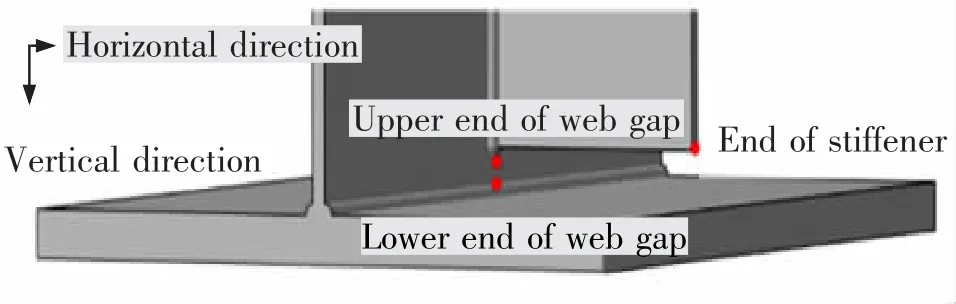
图4 位移选取点Fig.4 Selection point of displacement

以X 型横向作为横向联结系的主梁为例进行分析，提取各点随着车辆荷载纵向位置移动的位移变化如图5 所示。当车辆距离主梁截面较远时，各点之间的位移几乎一致，表明各构件之间不存在明显的约束作用，相应的应力也较小。但当车辆荷载靠近研究对象主梁时，各点之间的位移差明显。加劲肋上下两端的竖向位移基本重合，表明腹板间隙局部的竖向刚度较大，不会产生明显的面内变形。

图5 位移变化Fig.5 Displacement variation

为了便于分析，对比荷载纵向位置恰好位于该主梁正上方时的位移值进行对比，如表1 所示。不同主梁结构形式下，腹板间隙上下两端之间的水平位移、腹板间隙上端与加劲肋端部的竖向位移差值均超过0.03 mm 以上。相关研究表明，对于钢板梁桥腹板间隙细节，当腹板间隙的相对面外变形在0.013～0.025 mm，腹板间隙处的弯曲应力在10～97 MPa[19]。腹板间隙存在明显的“位移”与“转角”的共同作用。

表1 构件位移Tab.1 Component displacement mm

3 腹板间隙梁段计算模型建立与验证

3.1 模型建立

目前，对于疲劳性能与强度的评估方法，主要包括名义应力法、热点应力法以及缺口应力法。其中名义应力法是一种将材料力学中的应力分析和典型焊接细节疲劳强度相结合的一种评估方法，不考虑由于焊接所引起的应力集中现象，可根据结构力学计算方法获取。

已有研究表明钢板梁桥腹板间隙上端与下端会产生转动方向相同的弯矩，出现双向弯曲特征，这与两端固结的超静定梁杆的受力特征类似。Fisher[11]，Jaijch 等[13]也提出将腹板间隙简化为两端固结的梁杆，对腹板间隙的面外应力进行评估的方法。然而，上述方法仅考虑了腹板间隙的转角变形。根据前面的研究，腹板间隙端部会同时出现转角与位移变形。本文进一步将腹板间隙简化为两端固结的梁体，考虑其在转角与位移共同作用下的弯矩与剪力，计算模型如图6 所示，图中腹板间隙长度与厚度分别为g，t，腹板间隙上端转角与位移分别为θ，Δ。

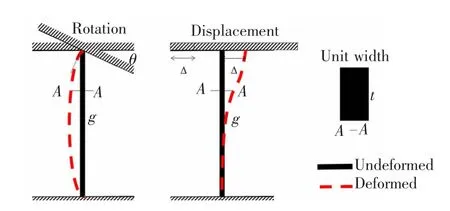
图6 简化模型Fig.6 Simplified model

由于腹板间隙较小，且实际结构的转角一般极小，在转角较小的范围内可以认为，转角的正切值与角度值一致，从而将转角与位移值进行关联，如图7 所示，得到转角与位移的关系

图7 转角与位移的关系Fig.7 Relationship between rotation and displacement

根据上述简化模型，选取单元宽度，以腹板厚度中心位置进行计算，同时考虑腹板间隙端部的转角与位移作用，由于钢梁厚度较大且长度较小，其刚度较大，将腹板间隙模拟为两端固结的梁段进行名义应力的计算。

3.2 双向弯曲特征验证

为了验证该“转角+位移”梁段计算模型的正确性，对腹板间隙表面的正应力进行分析，通过等截面单跨超静定梁杆端弯矩与剪力计算公式（表2）进行计算。表2 中，Mθ，MΔ分别为由于转角、位移产生的弯矩；Vθ，VΔ分别为由于转角、位移产生的剪力；i=EI/g，E为材料的弹性模量，I 为横截面对中心轴的惯性矩。

表2 弯矩剪力计算公式Tab.2 Calculation formula of bending moment and shear force

将转角与位移作用下的弯矩进行叠加，得到腹板间隙上下两端的弯矩值（Mu，M1），见式（3）。腹板间隙上下两端的弯矩均为负值，即在腹板间隙上端弯矩方向与转角方向相反。且上下两端弯矩方向相同，说明腹板间隙呈双向弯曲状态，这与现有研究结果中腹板间隙呈双向弯曲，且腹板间隙上端上表面受拉而下表面受压的应力状态一致。

此外，将腹板间隙上下两端的弯矩进行比值，发现上下两端的弯矩比例为1∶2。腹板间隙为等截面，且腹板间隙之间没有外力作用，正应力应与弯矩作用比例一致，确为线性变化，即腹板间隙表面两端正应力比例也为1∶2。腹板间隙的弯矩、方向及正应力分布如图8 所示。腹板间隙上表面1/3 高度处正应力为0。

图8 腹板间隙两端正应力特征Fig.8 Normal stress characteristics at both ends of web gap

3.3 模型正确性验证

为了证实上述正应力比例计算结果的正确性，通过腹板间隙表面正应力分布进行验证。考虑到腹板间隙长度对结构应力特征的影响，在子模型中设置了26，32，40，54，76.2 mm 共5 个子模型工况，计算腹板间隙表面上端至下端的正应力，如图9 所示。正应力随着与腹板间隙上端的距离逐渐减小变为负值，且在中间高度处存在正应力零点位置。

根据3.2 节分析，零点位置应位于腹板间隙的1/3 高度，然而仅考虑转角作用的模型，经过名义应力计算得到的零点位置则应位于腹板间隙2/3 高度处，绘制零点位置与腹板间隙长度关系，如图10 所示。分别采用实测应力数据与有限元计算结果进行验证。有限元计算数据选取图9 中的正应力零点位置。实测数据依据FHWA/PA-84-016 报告，该工程对钢桥腹板下翼缘端部的腹板间隙进行应力测试，布置3 个垂直围焊端部的应变片，不考虑靠近焊缝两端的非线性应力，以线性趋势表达腹板间隙的正应力变化，并进一步计算正应力零点位置[20]。基于本文有限元模型计算得到的零点位置基本为腹板间隙1/3 高度，而应力测试数据由于测试中不可避免的误差与应力集中的影响，零点位置存在一定偏离，但均在腹板间隙1/3 高度上下波动。而仅考虑腹板间隙端部的转角作用时，其计算结果与结构实际受力状态存在明显误差。对于腹板间隙构造，应同时考虑其“转角”与“位移”的变形作用，可以更准确的模拟腹板间隙的应力特征。

图9 腹板间隙表面正应力Fig.9 Normal stress on the web gap surface

图10 正应力零点位置Fig.10 Zero position of normal stress

4 腹板间隙应力作用特征分析

4.1 基于名义应力的剪应力正应力作用比例推导

腹板间隙上端，即腹板与竖向加劲肋连接焊缝的围焊端部是钢板梁桥最主要的开裂部位之一。基于第3 节中的模型，对该细节的应力特征进一步的分析。根据表2，将转角与位移作用下的弯矩与剪力叠加，得到腹板间隙上端的弯矩与剪力

由式（9）可知，腹板间隙上端的剪应力与正应力比值与荷载作用特征无关，仅与腹板间隙的构造尺寸相关，即与腹板厚度呈正比，与腹板间隙长度呈反比。

4.2 比例特征影响因素验证

4.2.1 荷载横向位置影响

根据4.1 节分析，腹板间隙剪应力与正应力作用比例与荷载作用无关。为了验证上述应力特征，提取有限元计算中不同横向荷载作用位置下，腹板间隙上端的正应力与剪应力，如图11 所示。

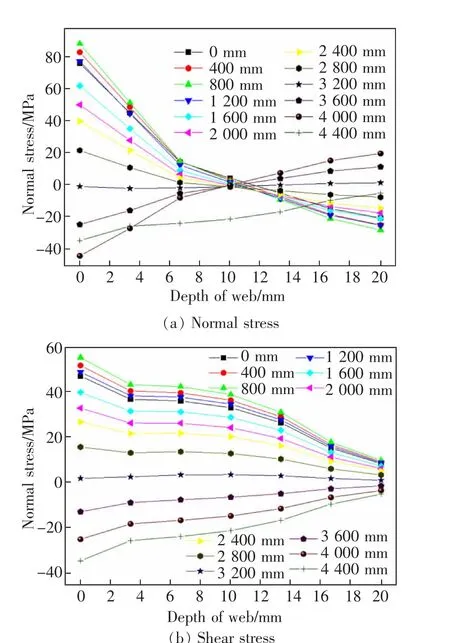
图11 横向荷载位置对应力的影响Fig.11 Effect of load lateral position on stress

实桥中，腹板与竖向加劲肋焊缝表面最易开裂，选取腹板间隙深度为0 的位置进行剪应力与正应力进行比例计算，见图12。当荷载位于双主梁之间时，正应力与剪应力的比值较为稳定，在0.6～0.7波动。就本文分析的钢板梁桥模型，车辆荷载在常规行驶路径下，横向荷载作用位置在±3 200 mm，剪应力与正应力比值的平均值为0.649，方差与标准差分别为0.000 271 与0.017，表示剪应力与正应力的比值相当稳定，即腹板间隙上端的剪应力与正应力比值不随横向荷载作用位置的移动而变化。

图12 横向荷载位置下剪应力与正应力作用比例的影响Fig.12 Effect of lateral load position on ratio of normal stress and shear stress

4.2.2 荷载纵向位置影响

车辆荷载纵向范围对结构应力的影响有限，仅当荷载在所分析细节桥跨内时，对主梁结构产生明显的应力作用，仅考虑荷载位于第二跨内时的应力变化，如图13 所示。随着荷载纵向位置的变化，剪应力与正应力变化趋势一致，且剪应力与正应力比值相对稳定，平均值为0.6 315，方差与标准差分别为0.0 373 与0.00 136。在纵向荷载主要作用位置下，腹板间隙端部的剪应力与正应力比值基本稳定，且与纵向荷载作用位置无关。

图13 纵向荷载位置下对剪应力与正应力比例的影响Fig.13 Effect of longitudinal load position on ratio of normal stress and shear stress

4.2.3 腹板间隙长度

根据式（9）计算结果，腹板间隙的剪应力与正应力作用比例与其长度呈反比。对不同腹板间隙长度下（16，26，32，40，54 mm 与76.2 mm）的正应力与剪应力进行计算，如图14 所示。除腹板间隙长度16 mm 以外，因其长度厚度比小于1，刚度特征发生了变化，其余腹板间隙长度下的正应力与剪应力均随腹板间隙长度的增加呈增大趋势。

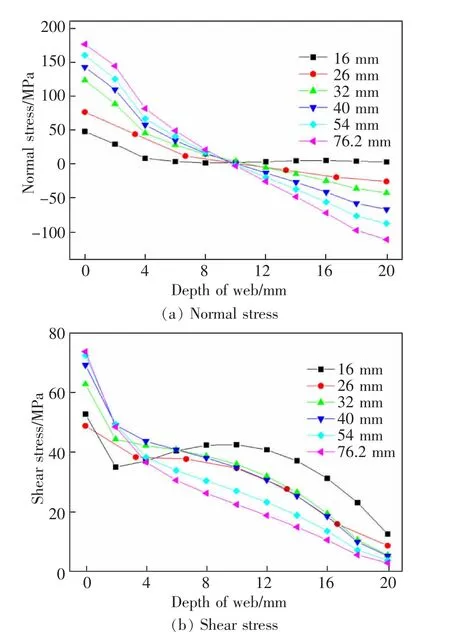
图14 腹板间隙长度对应力的影响Fig.14 Effect of web gap length on stress

将上述腹板上表面的剪应力与正应力进行比例计算，并绘制式（9）中的表达式，如图15 所示。有限元计算结果显示，随着腹板间隙长度的增加，剪应力与正应力的比值逐渐减小，并且其变化趋势与公式中的反比例函数关系一致。然而，在定量关系上仍存在明显差异，这主要是由于本文中提出的梁段计算模型是基于名义应力计算的结果，未考虑焊缝等构造导致的应力集中的影响。对于腹板间隙细节应采用热点应力等方法进行更细致的分析。

图15 不同腹板间隙长度的剪应力正应力比Fig.15 Ratio of normal stress and shear stress with different web gap length

4.2.4 腹板间隙厚度

根据式（9）计算结果，腹板间隙端部的剪应力与正应力作用比例与其厚度呈正比。分别计算腹板厚度为16，20 mm 以及24 mm 时的正应力与剪应力，如图16 所示。腹板间隙上表面的剪应力与正应力比分别为0.505，0.530 与0.531。然而，3 个试件的厚度比为1∶1.25∶1.5。剪应力与正应力比例与试件的厚度比并非呈正比例关系。导致该差异的原因在于，腹板间隙上端为焊接构造，剪应力分布特征并不等同于等截面剪应力分布的抛物线形式。后续还将对围焊端部的剪应力分布特征开展进一步的分析。