Model-Free Predictive Control for a Kind of High Order Nonlinear Systems

Ye Tian and Baili Su

(School of Engineering College, Qufu Normal University, Rizhao 276826, Shandong, China)

Abstract: For a type of high-order discrete-time nonlinear systems (HDNS) whose system models are undefined, a model-free predictive control (MFPC) algorithm is proposed in this paper. At first, an estimation model is given by the improved projection algorithm to approach the controlled nonlinear system. Then, on the basis of the estimation model, a predictive controller is designed by solving the finite time domain rolling optimization quadratic function, and the controller’s explicit analytic solution is also obtained. Furthermore, the closed-loop system’s stability can be ensured. Finally, the results of simulation reveal that the presented control strategy has a faster convergence speed as well as more stable dynamic property compared with the model-free sliding mode control (MFSC).

Keywords: nonlinear system; compact dynamic linearization (CDL); model predictive control (MPC); model-free control (MFC); projection algorithm

0 Introduction

Thecontrollerdesignisusuallyfoundedonthemathematicalmodelwiththecontrolledprocesspreciselygiveninmoderncontroltheory.However,themodel-basedcontrolalgorithmsoftencannotachievetheexpectedeffectintheactualproductionapplicationduetotheunmodeleddynamicsanduncertainvariousfactorsinthemodelingprocess.Inthewakeoftheprogressofscienceandtechnology,becauseoftheincreasingscaleofindustrialproductionandtheincreasingcomplexityofthenonlinearsystemintheactualproductionprocess,wecannotgetaprecisesystemmodelinrelationtothecontrolledprocess.Therefore,weconsiderdesigningcontrolmethodswhicharenotbasedonprecisemathematicalmodels.

MFCmethodisakindofdata-drivencontrol(DDC)methods.Itonlyusesthecurrentandpastinput/outputdata(IOD)ofthecontrolledprocesstopredictfuturedynamics.ThemainMFCmethodsintheearlystudiesarebasedonthespeciallinearsystemstructureandthegradientestimationmethodbasedontheIODofthecontrolledsystemforgeneralnonlinearsystems.Just-in-timemodelingisakeystepindata-drivencontrol.Just-in-timemodeling,alsocalledtheinstance-basedlearning[1],on-demandmodel[2],ordelaylearning[3],isfirstproposedinRef.[4].Therefore,asaneffectivecontrolmethod,scholarshavecarriedoutextensiveresearchonMFCmethodinrecentyears.Ref.[5]putsforwardamodel-freeadaptivecontrolmethod(MFAC)inlinewiththeCDLtechnologyregardingakindofHDNS.ThedesignofthecontrolleronlyutilizestheIODofthecontrolledobjecttoensurecontrolperformanceandtheconvergencetowardstrackingerrors.Inallusiontoakindofordinarydiscrete-timenonlinearsystemswhicharemulti-inputandmulti-outputsystems(MIMO),Ref.[6]proposesadata-drivenMFACalgorithmbasedonpseudo-partialderivatives,andtheCDLandpartialdynamiclinearization(PDL)arediscussedrespectively.Ref.[7]changesthenonlineartime-varyingtrafficnetworkdescriptionintothesimplifieddatamodel,sothatthemodel-freemodelhasbeensuccessfullyappliedinpractice.

MPCisafinitetimeoptimizationcontrolmethodgeneratedfromindustrialprocess.MPCincludesthreefundamentalcharacteristicswhicharemodelprediction,rollingoptimization,andfeedbackcorrection.Itisacontrolstrategythatusesthesystemdynamicmodeltopredictthefuturesystemresponse.BecauseMPChastheadvantagesoflowrequirementonmodel,easyon-linecalculation,andoptimizationdesign,inrecentyearsmanyscholarshavecombinedMPCwithmodel-freemethodtoproduceabatchofhigh-qualitycontrolmethods.Atthebeginningofthe21stcentury,somescholarscombinedMFACwithMPCandputforwardthemodel-freeadaptivepredictivecontrolmethod[8].However,thismethodrequiresthepredictionofthepan-modelfeaturevectorsatfuturemoments,andthecontroleffectisnotidealduetotheimpreciseprediction.Therefore,inrecentyears,ithasbecomeahottopicforsomeresearcherstousethelinearmodeldescribedbypseudopartialderivativematrix(PPDM)tocharacterizetheHDNS,andithasbeenappliedinvariousdomains,forexample,food,chemical,industry,aviation,andsoon.Ref.[9]presentsanMFACmethodforakindofnonlinearsystemswhicharedepictedbynonlinearautoregressivemovingaveragemodelbasedonRefs.[5]and[6].Ref.[10]studiestherelationshipbetweenMFPCandMPCwhichisgroundedonparameterestimation.Thenoisepollutionconditionisaddedintothehypothesis,andtheobtaineddataareoptimizedtoobtainmoreaccuratedata.Ref.[11]introducesanMFPCmethodfornonlinearsystemsbasedonpolynomialregressionexpression.TheMFPCmethodbasedonthelinearregressionvectorofIODisextendedtothepolynomialregressionvector.Ref.[11]isgeneralizedtoMIMOsystemsinRef.[12]whichrealizesitsapplicationinwastewatertreatment.Ref.[13]proposesamodel-freepredictivehybridsensitivity(PHS)H∞controlmethodbasedontheIODtoobtaintheoptimalPHSperformancebyusingthemaximumminimizationmethod.Furthermore,itappliesthecontrolstrategytothesolarpowergridsystem.However,theseMFPCalgorithmsoftenrequirealargeamountofcomputationandneedtosolvecomplexnonlinearprogrammingproblemsonline,soitisnotfaciletoacquiretheexplicitanalyticsolutions.InallusiontoakindofHDNSwhichhaveunknowndynamics,anMFSCapproachbasedonthesystem'sIODandtheconstructionofanadaptiveobservertodeterminethePPDMisproposedinRef.[14].Butthismethodhassomelimitationsinsystemselectionandhashigh-frequencytremor,sothecontrolofsomecomplexindustrialprocesseswillbecomedifficultandunsatisfactory.

ThispaperproposesanMFPCmethodforakindofHDNSwhichareapproachedbyanestimationsystem.Comparedwithothernonlinearcontrolalgorithms,itnotonlyrequireslesscomputation,butalsosolvestheoptimizationproblem,andstablestheclosedloopsystem.Theremainderofthearticleisdescribedbrieflyasfollows:inSection1,theCDLtechniqueisusedtoestablishadata-drivenmodelregardingHDNS.InSection2,anestimationsystemisdesignedandtheestimationofthePPDMisgiven.InSection3,thepredictionmodelisestablished,andtheappropriatecontrollawisobtainedafterrollingoptimization.Then,therationalityandeffectivenessofthemethodareverifiedviathesimulationresultsfromSection4.Intheend,thesumming-upisarrangedinSection5.

1 Question Description

ConsidertheHDNSbelow,whichhasanextendedexternalinput:

(1)

wherexi∈R(i=1,2,…,n),y∈R,andu∈Rarestatevariables,output,andinputofthesystem,respectively.txi,jandtudenotesystemorders.Thefunctionsfi(·)(i=1,2,…,n)representtheunidentifiedsmoothfunctions.

CDLmethodintroducestheconceptofPPDMandpseudo-order,andonlyconsidersthedynamicrelationshipbetweenthenextmoment’soutputvariationandthecurrentmoment’sinputvariation.CDLtechnologycanbeusedtotransformtheHDNSintoalineartime-varyingdynamicdatamodelwithscalarparameters.InordertoadopttheCDLapproach,wemakethefollowingassumption.

Assumption 1Partialderivativeregardingfi(·) (i=1,2,…,n-1)inrelationtox1(t), …,xi-1(t),xi+1(t),andpartialderivativeregardingfn(·)inrelationtox1(t),…,xn-1(t),u(t)keepcontinuous.Justforthesakeofpresentation,leti=1，2，…,n,ifi=n,then,xn+1(t)=u(t).

Theorem 1Groundedontheaboveassumption,system(1)canberepresentedasthefollowingform:

ΔX(t+1)=Η(t)Λ(t)

(2)

where

ΔX(t+1)=[Δx1(t+1),…,Δxn(t+1)]T

Λ(t)=[Δx1(t),…,Δxn(t),Δu(t)]T

Δxi(t+1)=xi(t+1)-xi(t)

Δu(t)=u(t)-u(t-1)

whereH(t)∈Rn×(n+1)standsforPPDM,γijrepresentsγij(t).

ProofLet

xl-1(t-txl-1,i),xl(t-1),xl(t-1),…,

xl(t-txli),…,xi+1(t),…,xi+1(t-

txi+1,i))(l=1,…,i-1,i+1)

Fromsystem(1),theequationisrepresentedasfollows:

Δxi(t+1)=ϑi+ξi

(3)

where

(4)

(5)

AccordingtotheLagrangemeanvaluetheorem,hereupon

(6)

Similarly,ξiisredescribedasfollows:

(7)

where

gib(x(t))=gib(x1(t-1),…,x1(t-tx1i-1),…,xb-1(t-txb-1,i-1),xb(t),xb(t-1),…,xb(t-

txbi-1),…,xi+1(t),…,xi+1(t-txi+1,i-1))

Inallusiontoeveryfixedt,thefollowingequationwhichinvolvethevectorωi(t)isconsidered.

gi,i+1=ωi(t)ΔΨ(t)

(8)

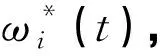
ξi=βi1(t)Δx1(t)+…+βi,i-1(t)Δxi-1(t)+

βi,i+1(t)Δxi+1(t)

(9)

where

(10)

FromEq.(9),thefollowingequationcanbeobtained:

IncombinationwithEqs.(6)and(9),Δxi(t+1)isrewrittenasfollows:

Δxi(t+1)=γi1Δx1(t)+…+γi,i-1Δxi-1(t)+

γi,i+1Δxi+1(t)

(11)

where

(12)

FromEq.(11),Eq.(1)canberepresentedinanotherformasEq.(2).

2 PPDM Estimation

Thetime-varyingparametersoftheunknownPPDMareestimatedusinganapproximationinthissection.Manyalgorithmscanbechosen,forexample,theleakagerecursiveleastsquaresalgorithm,theimprovedprojectionalgorithm,ortheleastsquaresalgorithmwhichhastime-varyingforgettingfactor.Here,animprovedprojectionalgorithmisusedtoestimatePPDM.

DividingH(t),Λ(t)intoblocks,then

X(t+1)=X(t)+Η1(t)Λ1(t)+Η2(t)Δu(t)

(13)

whereX(t),X(t+1)∈Rn,H(t)∈Rn×(n+1),H1(t)∈Rn×n,H2(t)∈Rn,Λ1(t)∈Rn,andΛ(t)∈Rn+1.

Anestimationsystemisdesignedasfollows:

(14)

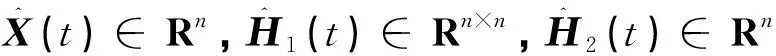
Let

f(x,u,Η1)=Η1(t)Λ1(t)+Η2(t)Δu(t)

(15)

ReferringtoRef.[15],theimprovedprojectionalgorithmisusedtoestimatePPDM.Thepseudopartialderivativeestimationcriteriaisselectedasfollows:

(16)

(17)

Similarly,

(18)

wheretheconstantμ1,μ2>0aretheweightfactor.

(19)

Remark 1：InEq.(16),asquaretermwithaweightingfactorofμ1isintroducedtopenalizelargeparametererrors,whichmakestheestimationalgorithmrobustwhenthereareindividualabnormaldata.ItcanbeseenfromEqs.(17)and(18)thattheintroductionofμ1,μ2canavoidtheoccurrenceofzerodenominator.

Remark 2：Thefactorsθ1andθ2areaddedtoEqs.(17)and(18)toenhancethegeneralityofthealgorithm.

3 MPC

3.1 MPC

Inthispart,theestimationsystem(14)isutilizedasapredictionmodeltodesignapredictioncontroller.

AccordingtoEq.(13),thesystemmodelcanbeexpressedasfollows:

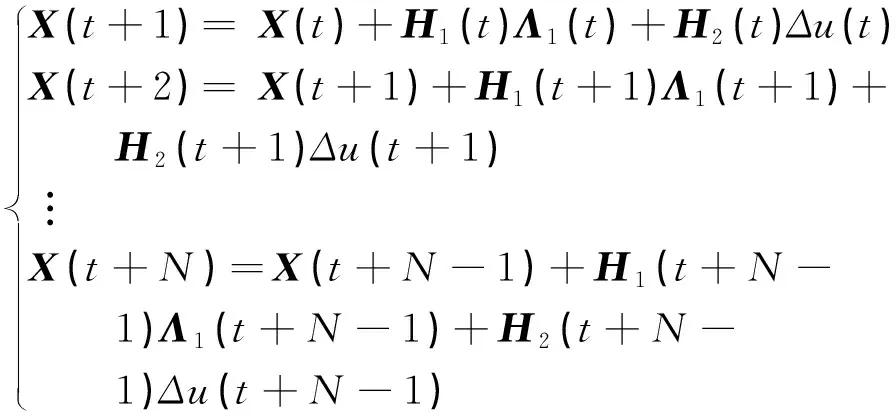
(20)

UnfoldingX(t+s)(s=1,2,…,N-1),whichareontherightsideofEq.(20),Eq.(20)canberewrittenasfollows:

XM(t)=PX(t)+Η1M(t)Λ1M(t)+Η2M(t)ΔU(t)

(21)

where

XM(t)=[XT(t+1),XT(t+2),…,XT(t+N)]T

P=[I,I,…,I]T

ΔU(t)=[Δu(t),Δu(t+1),…,Δu(t+N-1)]T

whereI∈Rn×nistheidentitymatrix,H1M(t)∈RnN×nN,H2M(t)∈RnN×N,P∈RnN×n,ΔU(t)∈RN,Λ1M(t)∈RnN,andXM(t)∈RnN.

Attimet,giventhepredictionofthestatesabouttheestimationsystem(14).Similarly,itcanbeinterpretedasfollows:

(22)

where

FromEqs.(21)and(22),thefollowingequationcanbededuced:

(23)

whereEM(t)=[ET(t+1),ET(t+2),…,ET(t+N)]Thequadraticfunctionofrollingoptimizationinfinitetimedomainisusedastheperformanceindex:

(24)

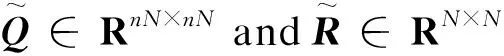
ReferringtoRef.[16],substituteEq.(23)toEq.(24).Thereis

(25)

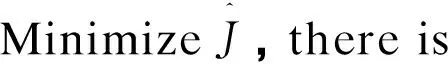
(26)

Let

u(t)=u(t-1)+ΞΔU(t)

(27)

whereΞ=[1,0,…,0],Ξ∈R1×N.Thesystemcanbestabilizedbyusingthecontroller(27).

3.2 Steps

Basedontheaboveanalyses,thebasicstepsoftheMFPCalgorithmproposedinthispaperareasfollows:

Step 4:Applyu(t)tosystem(13)toobtainthesystemstatesatthetimeoft+1.

Step 5:Lett=t+1andkeepuptoStep1.

4 Simulation

Inthispart,threesimulationexamplesareusedtoprovetheabovealgorithm.

Example 1:

Thetunneldiodeisacrystaldiodewhosemaincurrentcomponentisthetunneleffectcurrent.Ithassuchcharacteristicsashighspeedandhighrunningfrequency.Hence,thetunneldiodeiswidelyusedinsomeswitchingcircuitsandhighfrequencyoscillationcircuits.Inthispart,thenonlinearmodeloftunneldiodecircuitistakenasaninstancetoprovethefeasibilityoftheMFPCalgorithm.

ConsideringthetunneldiodecircuitwhichisdescribedinFig1,whereL,C,R,andDrepresentinductance,capacitance,resistance,andthetunneldiode,respectively,iandvarethecurrentandvoltagepassingthroughthecorrespondingcomponent.ThecharacteristicofthiscircuitisiD=h(vD).Definex1=vC,x2=iL,E=u.Inthiscase,L=5,C=2,R=1.5,andh(x1)=17x1-103x12+229x13areselected.AccordingtoKirchhoff'slawofcurrentandvoltage,thecontrolsystemisdescribedasfollows:

Fig. 1 Tunnel diode circuit

Fig.2 State x1

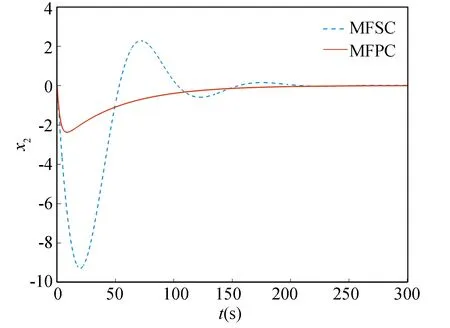
Fig.3 State x2

Fig.4 Input u

Fromthesimulationresultsofthetunneldiodecircuit,itcancometotheconclusionsthattheMFPCalgorithmproposedinthisarticlecanwarrantthatthesystemstatesarefinallystableforthediscretenonlinearsystemwithunknownsystemmodel.TheovershootoftheMFPCalgorithmissmallerandthesystemconvergesfasterincomparisonwiththeMFSCalgorithm.

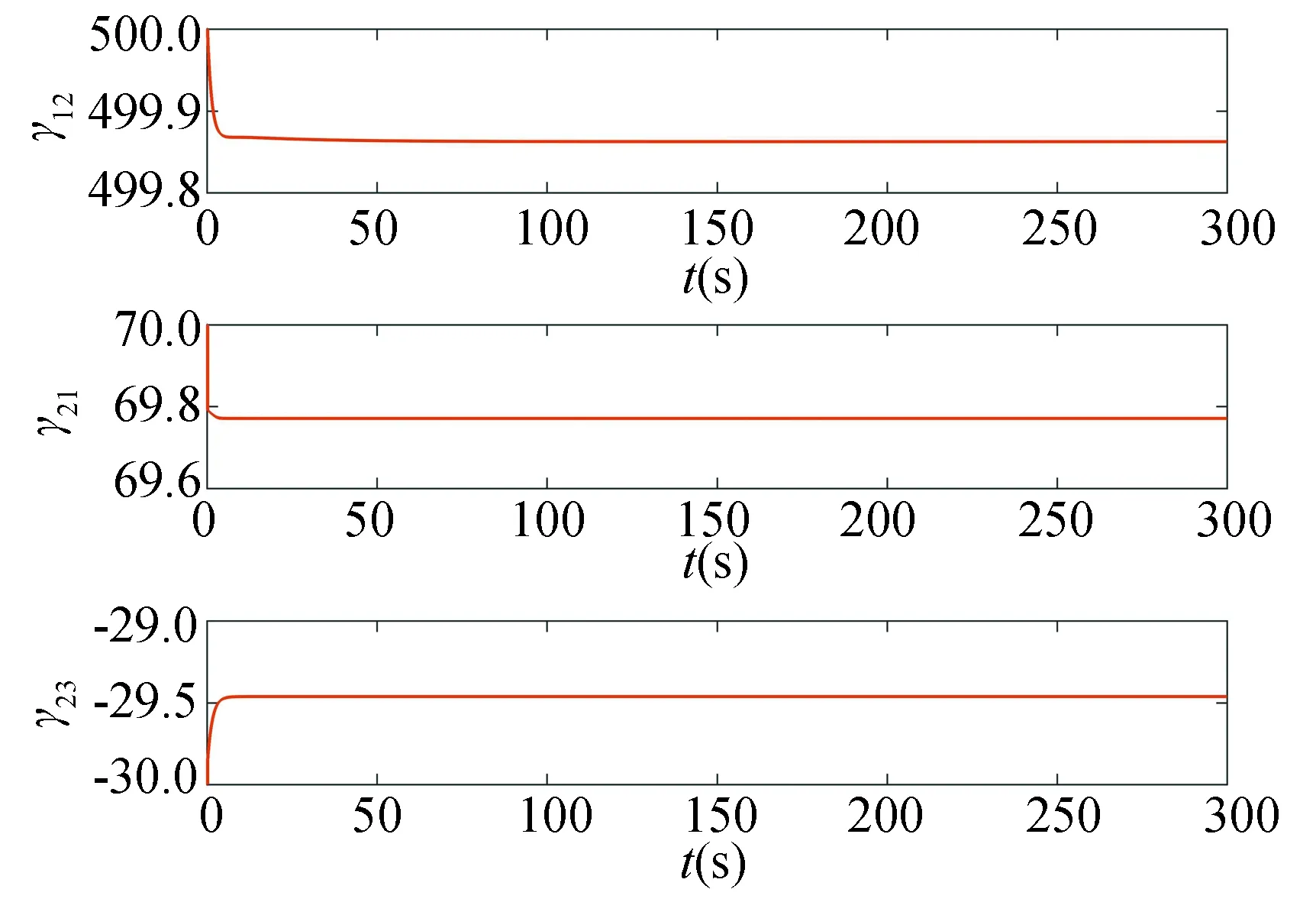
Example 2:

ThestirredtanksystemunderastandardmodelingassumptionistakenasaninstancetoprovethefeasibilityoftheMFPCalgorithm.Thecontrolsystemisdescribedasfollows:

Fig.6 State x1

Fromtheabovesimulationresults,itcanbeseenthatbothcontrollerscanwarrantthatthesystemstatesarefinallystableforthediscretenonlinearsystemwithunknownsystemmodel.However,theMFPCcanreachstabilityataboutt=100s,whiletheMFSCcanbestableataboutt=200s.Moreover,comparedwiththeMFSC,theMFPChaslessovershoot.

Fig.7 State x2

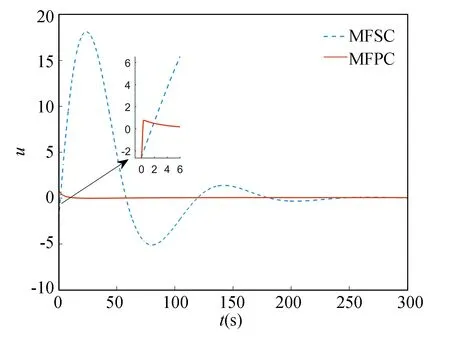
Fig. 8 Input u

Example 3 (Robust problem):

ForthesysteminExample1,anonlinearperturbationtermisaddedtothesystemmodel:

Assumingthatthediscretetime,initialvalue,andparametersremainunchangedasinExample1.ThesimulationconsequencesonthebasisoftheabovearegiveninFigs.10-12.

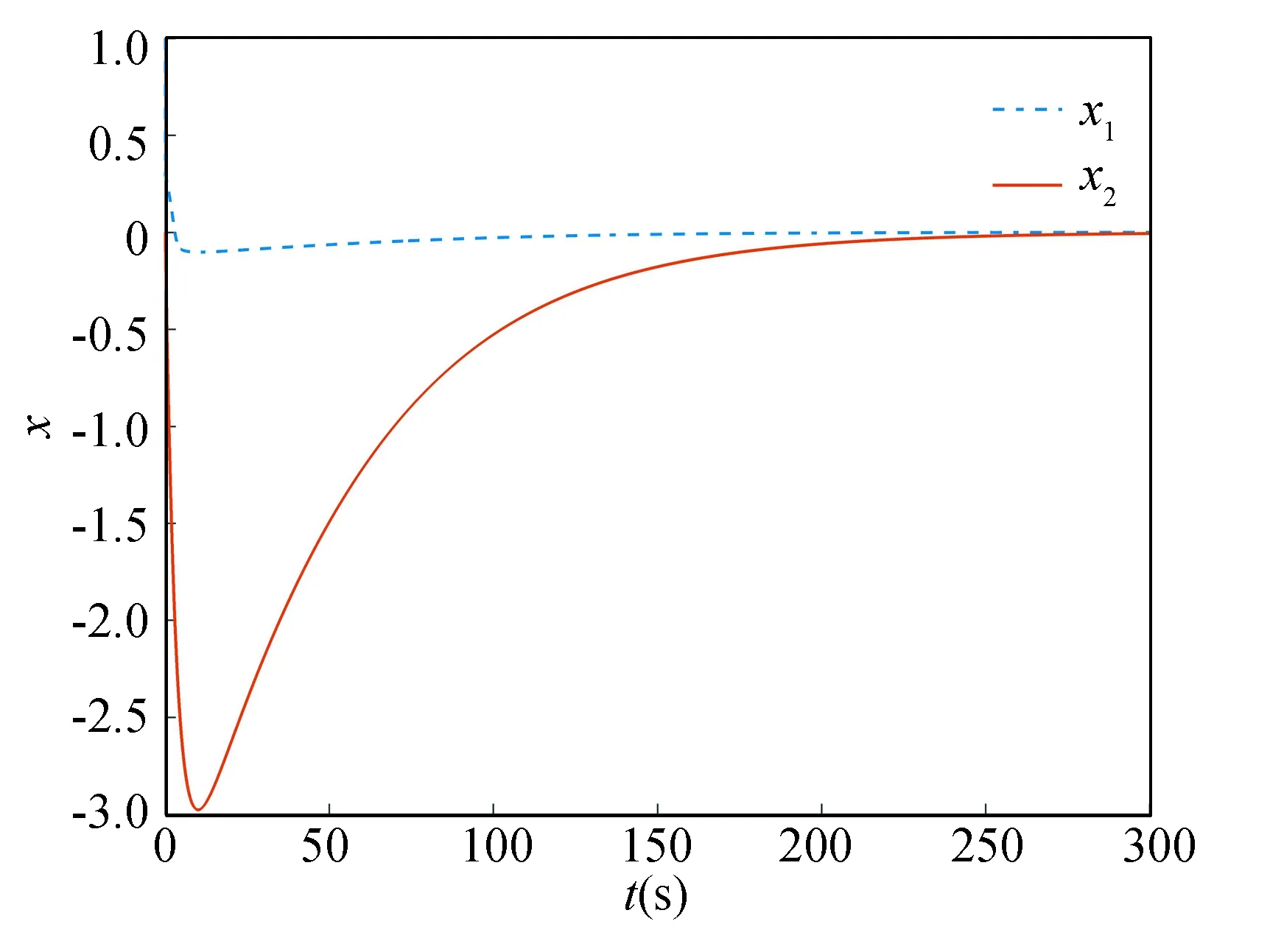
Fig.10 State x

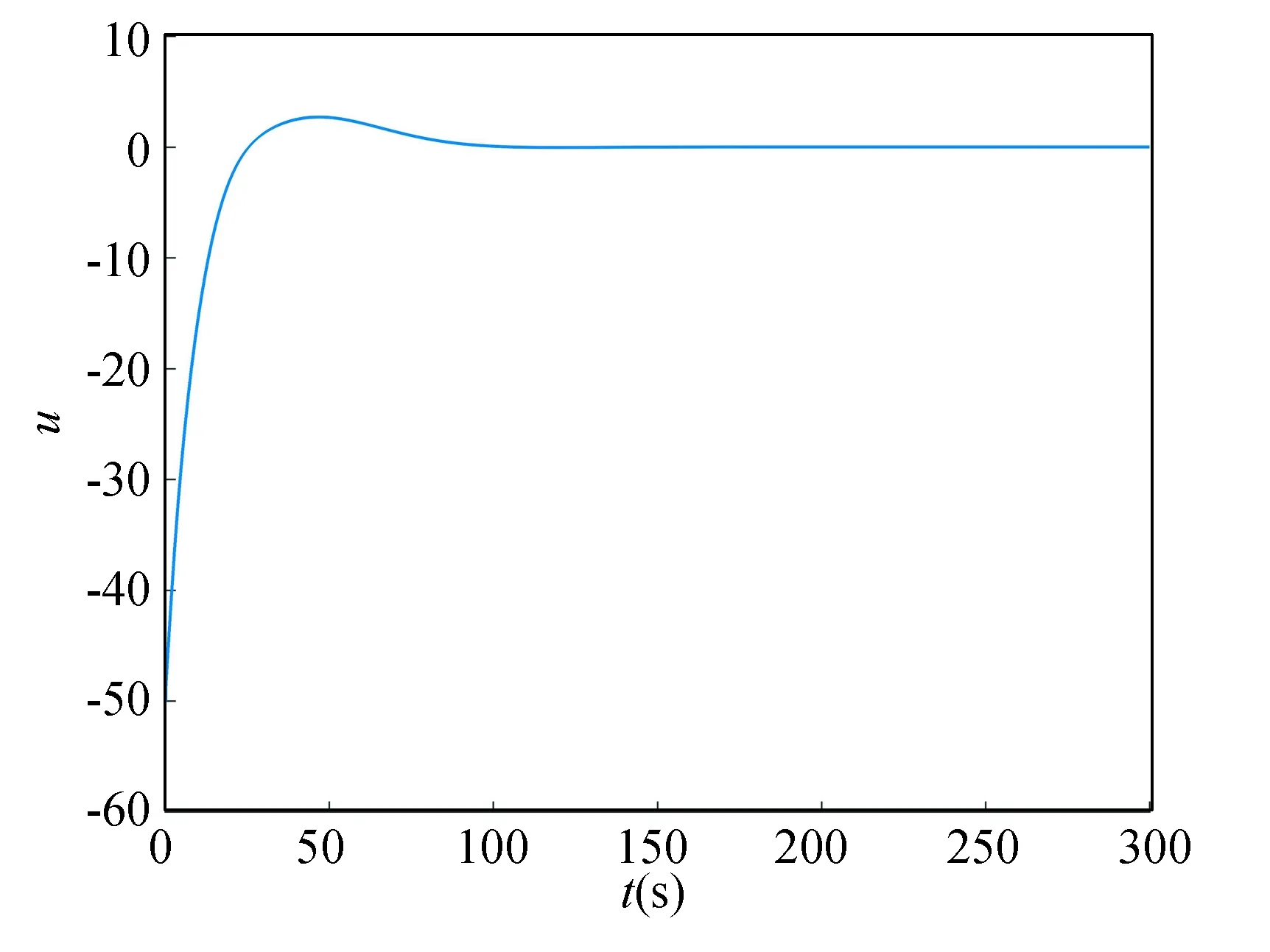
Fig.11 Input u

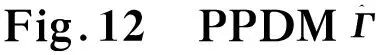
Itisclearfromtheabovesimulationfindings,theMFPCsuggestedinthischaptercanstillmakethesystemstableafteraddingthenonlineardisturbancetermintothesystem.Therefore,theMFPChasgoodrobustness.

5 Conclusions

Inthisarticle,anMFPCmethodisdevisedforakindofHDNSwhosesystemmodelsareundefined.Thesystemexpressedbypseudo-partialderivativematrixisobtainedbycompactformdynamiclinearizationmethod.Theimprovedprojectionalgorithmisusedtodesignanestimationsystemtoapproximatethecontrolledsystem.Anappropriatepredictivecontrollerisdesignedandtheexplicitanalyticalsolutionofthecontrolisobtained,whichfinallymakesthesystemstable.TheMFPCapproachhasexcellentrobustnessandstabilityaccordingtothesimulationconsequences.ComparedwiththeMFSCmethod,theMFPCmethodproposedinthispaperhassmallerovershootandfastersystemconvergence.Futureworksgroundedonthisarticleshouldcomprise:

1)expandingtheproposedMFPCtoMIMOnonlinearsystems;

2)thecontrolproblemsofotherspecialtypesofnonlinearsystemssuchasfractionalordersystemswithtimedelay.