Characteristics of Convection Heat Transfer in Power-Law Fluid Saturated Porous Media Channel

Xingwang Tian, Kun Zhang, Feng Liu*, Ping Wangand Shiming Xu

(1. School of Ocean and Civil Engineering, Dalian Ocean University, Dalian 116023, China;2. School of Energy and Power Engineering, Dalian University of Technology, Dalian 116024, China)

Abstract: Considering Brinkman-Forchheimer extended Darcy flow and local thermal non-equilibrium effect, a general model of forced convection with viscous dissipation in power-law fluid saturated porous media channel was established. The dimensionless temperature profiles and Nusselt number were numerically solved using the classical fourth-order Runge Kutta method under a constant heat flux boundary condition. The conclusion showed that the fluid-solid temperature distributions were significantly affected by dimensionless Bi, k, Da, Br, and F, and the effects of power-law indexes on convection heat transfer characteristics were also non-negligible.

Keywords: viscous dissipation; power-law uid; porous medium; thermal non-equilibrium; numerical simulation

0 Introduction

Flow and heat transport through porous media is widespread in natural system and engineering practice[1-3]. Two types of models for the energy equation were commonly described in various heat transfer process, involving local thermal equilibrium (LTE) or non-equilibrium (LTNE) model[4-6]. Using LTE and LTNE models respectively, Lee and Vafai[7]obtained and compared the exact temperature solutions of thermal transfer in a porous media channel. The thermal bifurcation phenomenon in a forced convection porous medium channel by employing LTNE model was analyzed by Yang and Vafai[8]. Considering the Darcy-Binkman-Forchheimer flow, Jiang and Ren[9]used LTNE model to discuss forced convection process in a porous media channel. A metal foam microchannel heat sink was constructed by Li et al.[10], and the heat transfer characteristics were numerically investigated using Brinkman extended Darcy and LTNE model. Based on fully developed flow and LTNE model, Xu[11]theoretically investigated the flow inertia, velocity jumps, and thermal slips in a microchannel partially filled with micro-porous media. Using LTNE model, Shen et al.[12]numerically studied the heat exchange characteristics of copper metal foam with different shapes in micro channels. Based on the Brinkman-Darcy momentum equation, considering viscous dissipation effect, Chen and Tso[13]numerically simulated the forced convection process using LTNE model in a porous media channel, and gained the fluid-solid temperature distributions with invariant heat flux.

Most initial research is based on Newtonian fluid. In numerous practical engineering applications, many fluids belong to the category of non-Newtonian fluid, such as blood and cell fluid in human body, slurry, pigment, paint, and industrial grease in chemical production, milk, and beverage in food industry, showing rheological properties of non-Newtonian fluid[14-15]. In the study of Thayalan and Huang[16], the momentum boundary layer integral method was used to solve the velocity distribution and the temperature distribution using LTNE model. The effects ofDa,n,Bi, andkon convection heat transfer were analyzed. However, the inertial effect and viscous dissipation effect of non-Darcy flow were not considered. Using Brinkman-Forchheimer extended Darcy flow model, Tian et al.[17]compared and analyzed three different viscous dissipation terms on forced convection thermal characteristic of power-law fluid in a porous media channel, but did not take into consideration fluid-solid temperature difference.

To strengthen heat transfer of tube-fin heat exchangers[18]or heat dissipation of microelectronic equipment, microchannel cooling technology using nanofluid is an effective solution. For example, for the convection heat transfer process of magnetic nanofluid[19-20]in porous microchannels, the non-Newtonian characteristics of nanofluids[21-22], LTNE effects, and other micro scale effects[23](such as viscous dissipation effect of nanofluids, nonlinear drag inertia effect, thermal dispersion effect, etc.) may need to be considered concurrently.

In summary, for the rheological characteristics of power-law fluid, there are few reports on the thermal transport in porous media including fluid-solid temperature difference, Darcy-Brinkman-Forchheimer flow, and viscous dissipation effect at the same time. In this paper, a convection model of power-law fluid in porous media channel is established. The effects of dimensionless parameters, such asBi,k,Br,Da,F, andnon temperature distribution and heat transfer characteristics are analyzed numerically.

1 Physical Mathematical Model

In this study, as shown in Fig. 1, an infinite parallel channel of height 2Hwas investigated. Considering the fully developed steady state of two-dimensional laminar flow heat transfer, thez-direction flow heat transfer is not considered (the width of the model is much larger than the height, and the conditions in the width direction are uniform and symmetrical). Assume the fluid is a single-phase, incompressible power-law fluid, the porous skeletons are rigid and isotropic, and the fluid and skeletons are in local thermal non-equilibrium. Except for the fluid viscosity, the themo-physical properties of the fluid and solid phases are considered constant. The velocity gradient along flow direction (inx-direction) is infinitesimal, and the chemical reaction, radiation heat, and the axial conduction are ignored.

The Forchheimer-Brinkman extended Darcy's law by modifying the momentum equation for power-lawuid[24]is expressed as

(1)

Dimensionless parameters are defined as follows:nrepresents the power-law index, transverse coordinateY=y/H; centerline velocityuc=(K*dp/(μdx))1/n; characteristic velocity based on centerline velocityU=u/uc; inertial parameterF=ρbK*(uc)2-n/μ;DanumberDa=K*2/(n+1)/H2/ε2n/(n+1).Then Eq. (1) with its boundary conditions is non-dimensionalized as

(2)

Fig. 1 Model of the considered problem

The corresponding energy equations are written as

(3)

(4)

(5)

whereTf,Ts,ks,eff,kf,effare fluid-solid temperature and thermal conductivity, respectively;Ωis representative of different viscous dissipation, involving Darcy term (internal heating), Al-Hadhrami term (frictional heating), and Forchheimer term (nonlinear drag power);hsfandasfare interface heat transfer coefficient and specific surface area, respectively.

(6)

(7)

Substituting Eqs. (4), (6), and (7) into Eq. (3), combining with Eq. (5), and integrating along the channel cross section, the following energy equation is obtained:

(8)

When the channel wall has finite thickness and the thermal conductivity is relatively high, under the fully developed steady state of two-dimensional flow heat transfer,θf=θs=θw, and considering axisymmetric boundary conditions, the corresponding dimensionless boundary conditions can be justified by

Y=0,U=U'=0,θf=θs=0

(9a)

Y=1,dU/dY=dU'/dY=0,∂θf/dY=∂θs/dY=0

(9b)

It is noteworthy thatBrcharacterizes the intensity of the viscous dissipation (Br=0, which indicates no viscous dissipation). It can be seen from the above expression that the viscous dissipation effect is closely related toBr,Da,F, andn.The Nusselt number[25]can be evaluated as

(10)

For LTE model,θf=θs. According to Eqs. (8) and (9), the dimensionless Nusselt number can be rewritten as follows:

(11)

The difference between LTE and LTNE models can be evaluated asE=NuLTE-Nu

2 Numerical Methods and Solvers

From the expressions of momentum equation and energy equation, it can be deduced that when the inertia flow and viscous dissipation effect are considered, there is a strong nonlinear effect of non-Darcy flow in porous media, which must be solved by numerical method. To do this, Eqs. (2) and (8) are first recombined and reduced to first order differential Eqs. (12). Obviously, this is a boundary value problem of ordinary differential equations. Then, assuming the initial value and a reasonable step size (0.01), the classical Runge Kutta method is used to carry out variable alternating numerical iteration from 0 to 1 until the iteration accuracy (10-5) and the boundary condition Eqs. (13) are satisfied. The parameters defined are as follows:

y1=U(Y),y2=(dU/dY)n

y7=Um,y8=(Um)n+1

y13(f)=θ(f)(Y),y13(s)=θ(s)(Y)

y14(f)=dθ(f)/dY,y14(s)=dθ(s)/dY

and

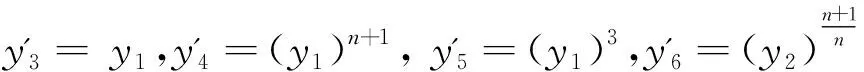
y'7=y'8=y'9=y'10=y'11=y'12=0,y'13=y14

y'14(s)=Bi(y13(s)-y13(f))

(12)

y7(0)=y3(1),y8(0)=(y3(1))n+1

y9(0)=(y3(1))3,y10(0)=y4(1)

y11(0)=y5(1),y12(0)=y6(1)

(13)

Then the expression of theNunumber can be obtained by the Eqs. (10), (11), and (12):

(14)

(15)

To prove the validation of the numerical program, the present solution with indirect decoupling analytical solution by Wang et al.[1]is compared in Fig. 2, which illustrates dimensionless fluid-solid temperature profile with varying Biot number andknumber along the cross section whenDa=0.1,Br=0, andF=0. It can be seen that the present numerical predictions and the work by Wang et al.[1]are in good agreement.

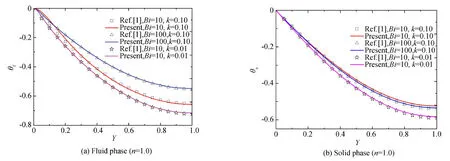
Fig. 2 Validation and comparison of present solution with indirect analytical solution (Da=0.1, Br=0, F=0)

In order to further verify numerical solution, supposeBr=F=0,θ(f)=θ(s)(assuming LTE model). Whenn=1 (Newton fluid),Da≤0.001, the value ofNuis 5.92, which is in line with the conclusion that when Darcy is a small number (i.e., piston flow,Nuis close to 6); whenDa≥1000, the simulation result,Nu=4.121, is also consistent with the conclusion that when Darcy is very large (i.e., parallel plate Poiseuille flow,Nutends to be 70/17), which is consistent with the research of Nield et al.[26]Whenn≠1 (non-Newtonian fluid),Da≥100, the simulation result of non-Newton fluid (n= 0.5, andn=1.5) are 4.380 and 4.010, respectively, which are in line with the conclusion of Chen and Tso[27].

3 Results and Analysis

To characterize the effects of dimensionless parameters on convection heat transfer characteristics, such asBi,k,Br,Da,F,n, and so on, there are many variables of velocity field and temperature field that can be solved. The velocity field is mainly affected by dimensionless Darcy number and Forchheimer number, and the dimensionless velocity profile of fluids for different power-law indexes with varyingDaandFnumber had been characterized and analyzed in Ref. [17]. The relationship of temperature distribution and the Nusselt number of power-law fluid of shear thinning are focused on here.

3.1 Impact of Bi

Fig. 3 describes the temperature profile of fluid and solid with change of Biot number and power-law indexes along the cross section in porous media. As depicted in Fig. 3, with the increase ofBi, the temperature difference of fluid and solid decreases gradually. WhenBi=100, the change of temperature difference is not obvious. It can be inferred that with a lagerBi(>1000), the temperature of the two phases tends to be the same. This shows that a largerBireduces fluid-solid thermal resistance and enhances convection heat transfer rate. Meanwhile, it is found that the direction of heat flux near wall is opposite, and the phenomenon of heat flux divergence[28]occurs. With the decrease ofBi, the phenomenon of heat flux divergence is more obvious. It can also be seen that with the decrease ofn, the fluid-solid temperature difference increases gradually, indicating the fluid-solid heat exchange is gradually weakened. It can be inferred that with the decrease ofn, the rheological property of pseudoplasticity is enhanced, the ability of intermolecular entanglement is strong, and the mesh structure formed between the molecules has larger resistance to the flow, which affects the velocity distribution. Meanwhile, the skeleton shear makes the viscosity dissipation between molecules further enhanced, reducing local convection heat transfer rate.

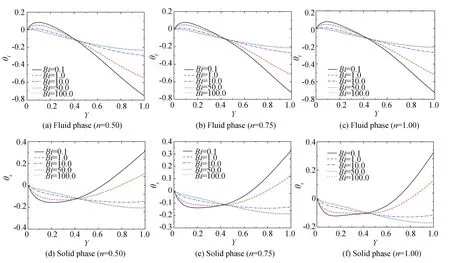
Fig. 3 Temperature profile for varied Bi(k=1,Br=1,Da=0.1,F=0.1)

3.2 Impact of k

The temperature profile with variable ofknumber and power-law indexes in porous media along the cross section is described in Fig. 4. With the increase ofk, both fluid and solid temperatures increase, but fluid temperature rises faster than that of solid, which makes the fluid-solid temperature difference slightly reduce. As shown in Fig. 4, it is found that with the decrease ofk(especially whenk<0.1), similar toBi, bifurcation phenomenon appears at the temperature gradient near the wall, which indicates that the heat flow divergence will occur under certain parameter combination. It can also be seen that with the decrease ofn, the fluid-solid temperature difference increases gradually, indicating that convection heat transfer rate decreases.

3.3 Impact of Br

Fig. 5 describes the temperature profile with the change ofBrand different power-law indexes in porous media along the cross section. It is shown that without the viscous dissipation terms (Br= 0), the temperature distribution of the two phases corresponding to three different fluids is almost equal, and the fluid-solid temperature difference is also small. When considering viscous dissipation effect (Br≠0), the fluid-solid temperature difference changes obviously with the increase ofBr, which can be explained that when numbers ofBr,Da, andFare not zero, the viscous dissipation effect generated by Darcy term, Alhdharami term, and Forchheimer term will overlap with each other. With the increase ofBr, the friction heat dissipation effect corresponding to Alhdharami term is more intense in the vicinity of the wall and decreases towards the channel center. The fluid temperature increases by heating effects[29], and the temperature gradient bifurcation phenomenon also appears near the wall. On the contrary, the internal heat dissipation generated by Darcy term plays a major role near the channel center, which reduces fluid temperature and increases solid temperature. It should be noted that there is a critical value ofBr, where the sign of the dimensionless temperature changes. It can also be seen that with the decrease ofn, the rheological property of pseudoplasticity is enhanced, and the temperature difference increases gradually, which shows that the convection heat transfer between two phases decreases somewhat, and the effects ofBron the pseudoplastic fluid is more obvious.

Fig. 4 Temperature profile for varied k (Bi=1, Br=1, Da=0.1, F=0.1)

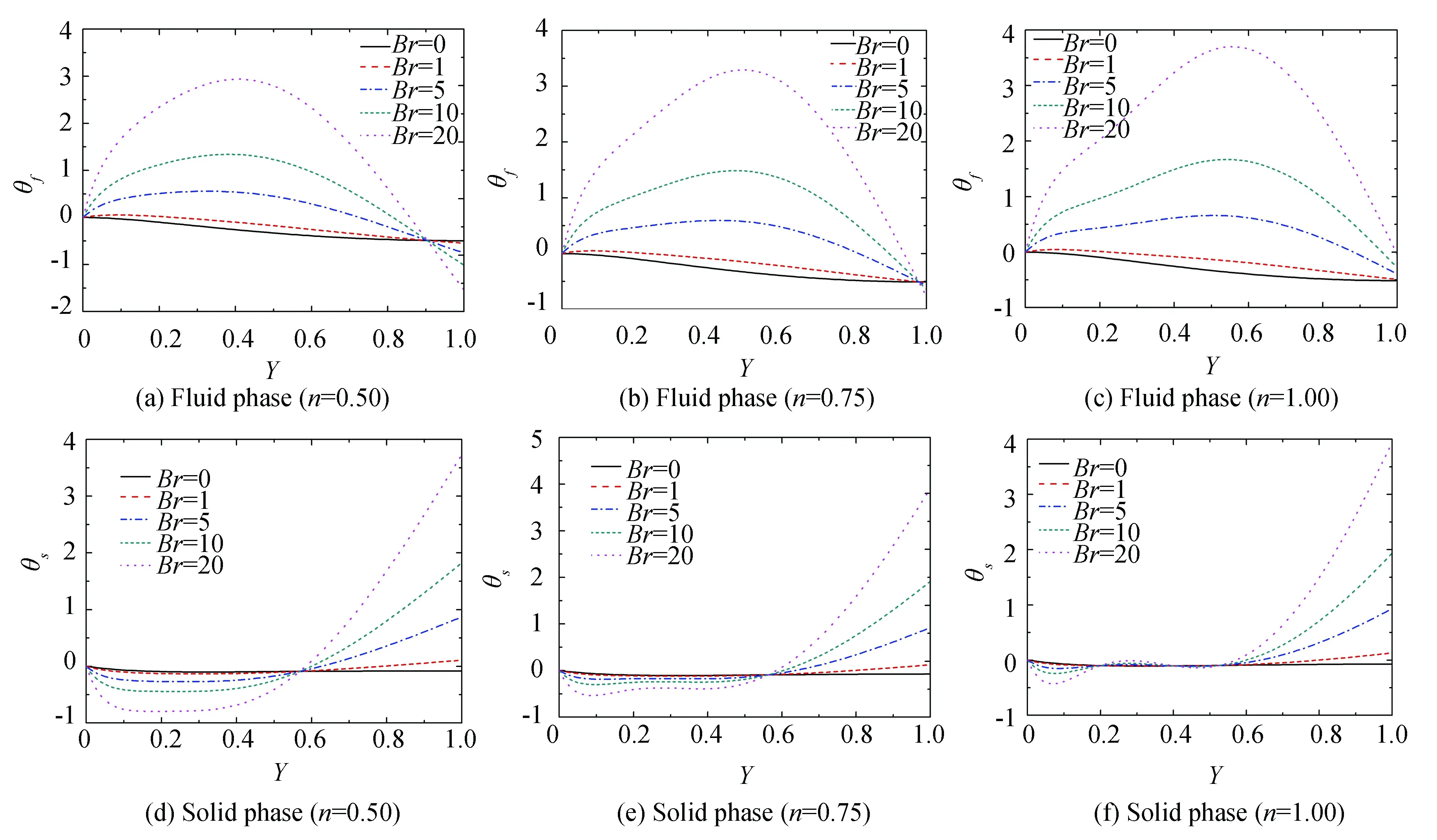
Fig. 5 Temperature profile for varied Br (Bi=1,k=1,Da=0.1,F=0.1)

3.4 Impact of Da

Fig. 6 plots the temperature profile with change of Darcy number and different power-law indexes along the cross section. It is observed that the fluid-solid temperature difference increases obviously with the increase ofDa. It can be explained that the largerDamakes the flow deviate from Darcy flow, and the non-Darcy flow area increases gradually. The velocity profile tends to be a parabola shape, the contact surface area of heat transfer decreases for the increased porosity, leading to the decrease of convection heat transfer rate, and the fluid-solid temperature difference gradually increases. Meanwhile, it is presented that whenDais small, the temperature difference increases with decrease ofn, indicating the convection heat transfer is weakened. On the contrary, with a largeDa, a smaller fluid-solid temperature difference is obtained with the decrease ofn, and the convection heat transfer is enhanced. The above results show that the range of influence ofDaon pseudoplastic fluid is small, which is consistent with Ref. [17].

Fig. 6 Temperature profile for varied Da(Bi=1,k=1,Br=1,F=0.1)

3.5 Impact of F

The temperature profile along the cross section with the change ofFnumber and different power-law indexes is depicted in Fig. 7. It is observed that increasingFinduces a slight increase of fluid and solid temperatures, and the phenomenon of heat flux divergence occurs near the wall. The flow speed increases with a largerF, and the flow resistance of solid matrix to the fluid increases. However, it can produce a larger velocity gradient near the wall, and the velocityeld will be modified by Drag forces dissipation effect. The influence of the change ofFon shear thinning fluid is also more obvious.

3.6 Impact of Parameters on Nu

The convection heat transfer characteristics with the change of related parameters (Bi,k,Br,Da,F, andn) is described in Fig. 8. The difference between LTE model and LTNE model is also evaluated. As described in Fig. 8(a), with the increase ofBiandn,Nuincreases gradually, while the difference ofEdecreases gradually with the increase ofBiand the decrease ofn. Contrary to Fig. 8(a), with the increase ofk,Nudecreases quickly as depicted in Fig. 8(b), while the difference ofEdecreases with the increase ofkand the decrease ofn. Fig. 8(a) and Fig. 8(b) show that the local thermal equilibrium is approaching with a larger number ofBiandk.

As illustrated in Fig. 8(c), because of the reverse of fluid temperature,Nuhas negative value, which shows that for a certain combination of other parameters, there is a maximum value ofNuwhen an appropriateBrnumber is selected. The general trend of the difference decreases with the increase ofBr. Fig. 8(d) shows that with the increase ofDa, the number ofNuandEdecrease gradually, but the decrease is becoming slower for pseudoplastic fluid. As depicted in Fig. 8(e), with the increase ofFandn, the number ofNuandEincreases gradually. It can be explained that the larger velocity makes the fluid flow deviate from the Darcy region, and LTNE effect is more significant.

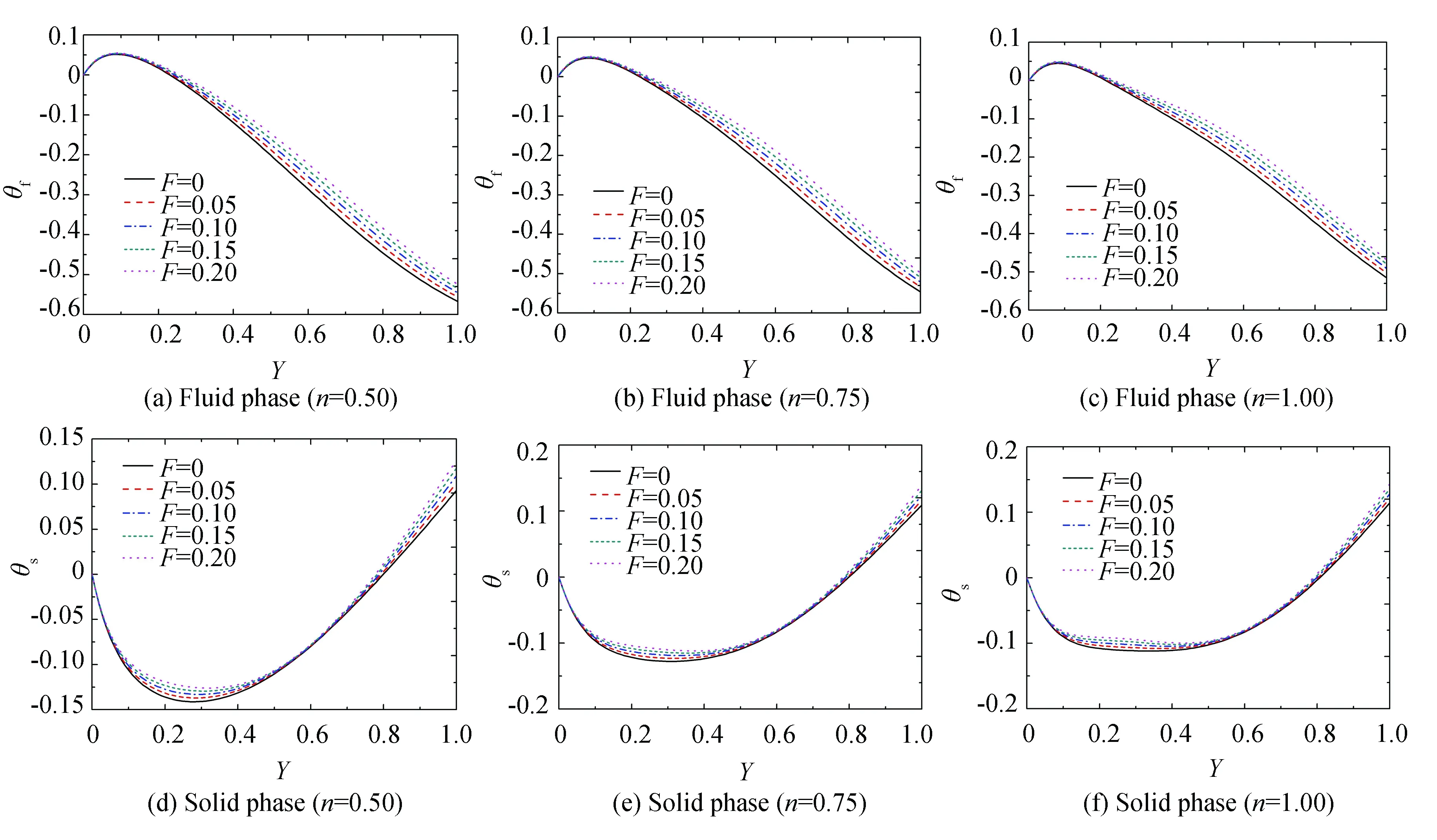
Fig. 7 Temperature profile for varied F(Bi=1, k=1, Br=1, Da=0.1)

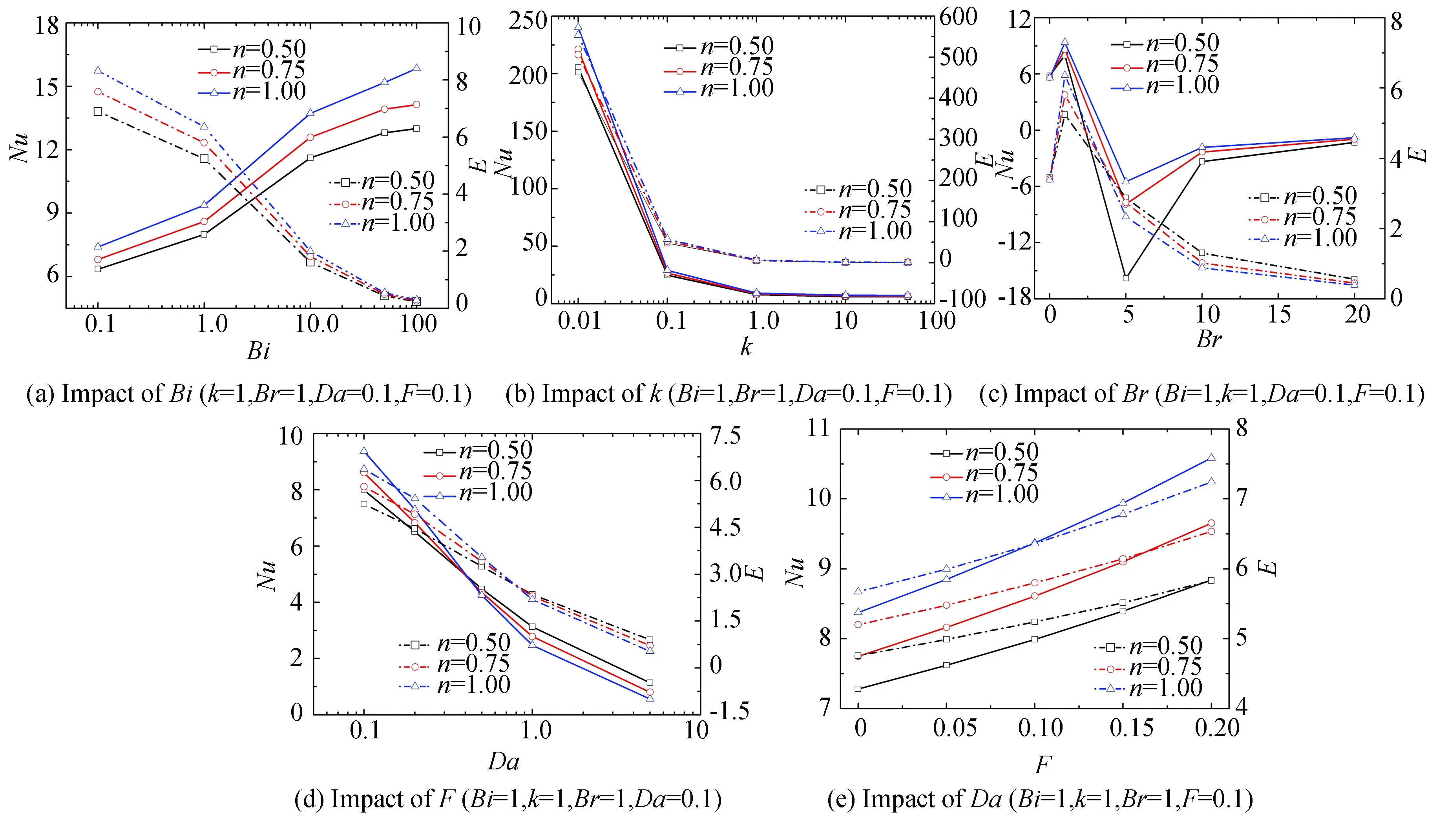
Fig. 8 Effects of related quantities on Nu

4 Conclusions

1) The general model of power-law fluid forced convection considering LTNE and viscous dissipation effects in a porous media channel was established. The calculation expressions of dimensionless fluid-solid temperature profiles and Nusselt number were derived with a clear relationship between physical parameters. The classical fourth-order Runge Kutta method was applied to numerically solve self-programmed solution under a constant heat flux boundary condition.

2) With a biggerBiandk, the temperature profile of solid was close to that of fluid, which means a local thermal equilibrium was reached. While with the decrease ofBi,k,Br,Da, and the increase ofF, the difference of temperature profile between fluid and solid increased gradually, intensifying the thermal non-equilibrium effect, and the fluid with different power-law indexes also had a non-negligible impact on the convection heat transfer characteristics.