电力变压器铁心振动特性分析*
2022-05-20徐秋元
王 青 李 怡 林 焱 徐秋元 连 雯
(1. 三变科技股份有限公司 台州 317100;2. 南昌大学信息工程学院 南昌 330031)
1 引言
电力变压器是电力系统中的重要设备,其可靠性与稳定运行是维持电网安全、正常工业生产与社会生活的重要保证[1]。振动是伴随变压器变换并传输交流电能过程中的固有现象[2]。在电力系统容量不断增长的背景下,电力变压器振动带来的问题也愈发突出:一方面,长期的振动将导致变压器结构件松动、绝缘磨损,危害设备健康;另一方面,因振动产生的噪声问题将影响周围人们的身心健康[3]。因此,变压器工作过程中的振动噪声水平成为了衡量变压器产品品质的重要指标,而在变压器设计与研究过程中,振动特性日益受到相关研究人员的重视[4-5]。
变压器的主要振动来源为绕组与铁心:绕组振动在变压器内部漏磁场中受到电磁力的作用,发生周期性振动现象;铁心振动是硅钢片在交变磁场的作用下,由磁致伸缩效应导致的周期性振动[6]。近年来,随着硅钢片性能以及铁心搭接技术的改进,硅钢片接缝处漏磁减小,在变压器的额定工作磁密范围内因漏磁产生的绕组振动往往会远小于因磁致伸缩引起的硅钢片振动,因此铁心振动成为了电力变压器正常工作时最主要的振动来源[7]。
现阶段,相关文献针对变压器铁心的磁致伸缩振动开展了相关研究工作,文献[8]从磁致伸缩的物理发生机制出发,建立了适用于晶粒取向性硅钢片的磁致伸缩本质模型,为准确模拟实际变压器铁心的磁致伸缩提供了依据;文献[9]通过修正铁心的动力学参数,利用能量法分配等效磁致伸缩力载荷,建立电磁-结构-声场耦合的仿真计算模型,为预估变压器铁心振动噪声提供了分析手段;文献[10]通过建立联结变压器的电磁——结构力场多物理场分析模型,为联接变压器振动噪声的预测及优化设计提动力参考;文献[11-15]从材料学角度针对硅钢片的磁致伸缩特性、电磁损耗等问题开展了建模与研究工作。除自身振动特性外,相关文献针对变压器正常工况下固有振动频率开展了研究工作,文献[16]利用弹性动力学理论,提出了一种高效的变压器绕组共振有限元分析模型;文献[17]分析了负载状态对变压器固有振动频率的影响;文献[18]利用“磁-机械”耦合理论,实现了变压器运行过程中电磁力激励下绕组振动特性模拟;文献[19-20]通过建立三维有限元分析模型,得到了正常工况下的振动波形与变压器固有频率。然而,通过分析现有文献可以看出,针对不同工况对电力变压器振动特性影响研究的相关工作仍然较少。
本文首先分析了变压器铁心磁致伸缩振动的机理,利用多项式拟合硅钢片的磁滞伸缩特性,随后利用有限元方法建立某企业生产的S13-M-400/10NX2型号配电变压器的三维电-磁-力多物理场分析模型,并结合实际应用环境分析不同工况下电力变压器的振动特性,总结了配电变压器的铁心振动规律。
2 变压器铁心电磁-力耦合机理
2.1 基本电磁参数与电磁耦合机理
S13-M-400/10NX2型号配电变压器正常工况下电气参数如表1所示。正常工作时,变压器铁心受到原边电压激励,三相瞬态激励电压Uk(k=u,v,w)表达式为

式中,Um为激励电压峰值。相应地,原边线圈中瞬态电流ik(k=u,v,w)表达式为

式中,Im为线圈中电流峰值。结合式(2)可以得到每相线圈中瞬态电流密度为

式中,S为导线截面积,可由表1中原边导线参数计算得出。最后,利用麦克斯韦方程组,实现计算模型中电场与磁场间的耦合
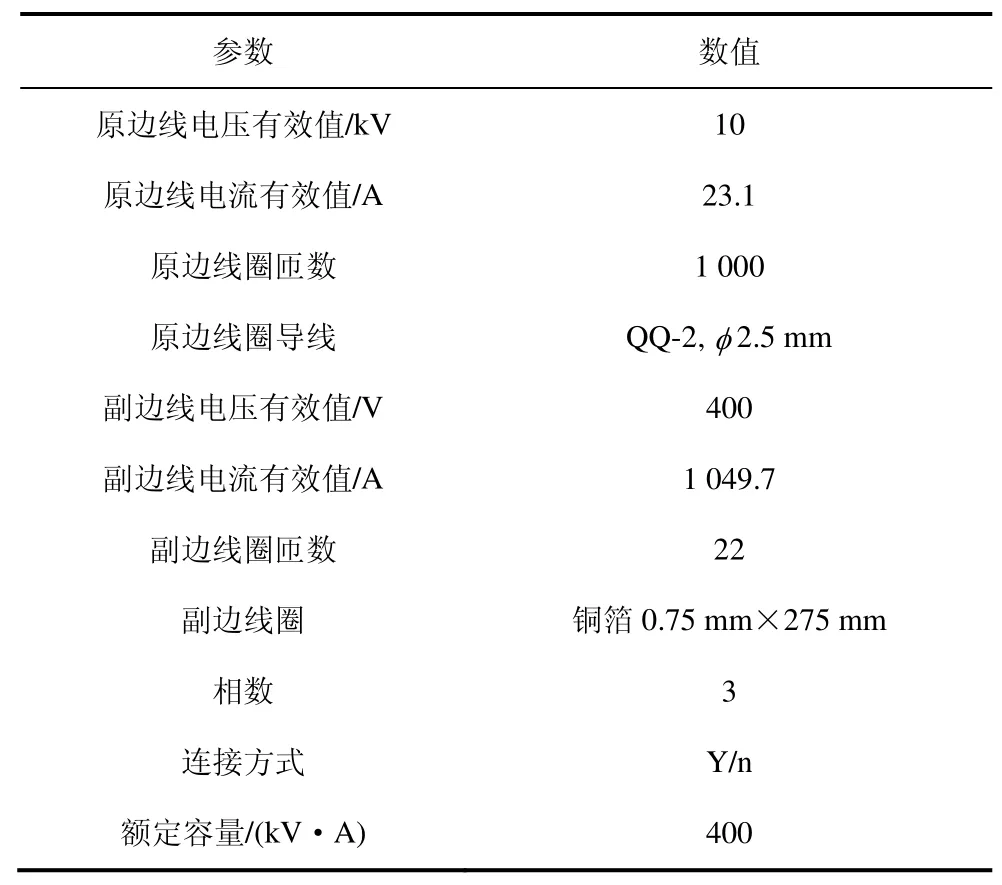
表1 S13-M-400/10NX2电力变压器电气参数

式中,H和B分别为磁感应强度和磁场强度;Jc、Jv分别为传导电流密度和运流电流密度;D为电通密度;q为电荷量。在电磁耦合过程中,硅钢片B-H曲线采用B23R080的磁化曲线数据。
2.2 变压器电-磁-力耦合机理
变压器铁心振动来源包括:硅钢片之间因感应出的涡流相互作用产生的电磁力导致振动以及硅钢片因内部交变磁通产生的磁致伸缩振动。
硅钢片间的相互电磁力作用示意图如图1所示。

图1 叠片间电磁力示意图
硅钢片间相互作用的电磁力满足麦克斯韦应力张量模型[3]

式中,Tij为第i号硅钢片与第j号硅钢片间的相互作用力;δij为Kronecer系数;ωm为叠片中的磁共能密度。硅钢片受到的电磁力F1为

式中,S表示包围铁磁材料结构件的闭合曲面。考虑到每一层叠片的厚度,可以将硅钢片的受力简化为二维平面下的计算,因此,F1可以简化为
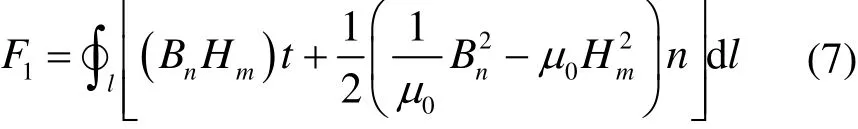
式中,t和n分别为积分路径的切向单位矢量以及积分路径的法向单位矢量;μ0为真空磁导率。
硅钢片的磁致伸缩是铁磁材料的基本性质,当其内部有磁通,材料磁畴因磁化加强而趋向于同一特定方向排列。一般材料用如式(8)所示的磁致伸缩系数(或应变系数)λ来描述磁场中铁磁材料的磁致伸缩效应。

式中,λ为磁致伸缩系数(或应变系数),单位为10−6;l为由铁磁材料构成的结构件原始尺寸;Δl为在磁场作用下因铁磁材料的磁致伸缩特性结构件改变的尺寸。与磁化曲线类似,硅钢片的磁致伸缩系数随磁通密度呈现非线性变化,硅钢片铁心磁致伸缩曲线如图2所示,磁致伸缩系数按照扎制方向与垂直方向进行区分,由图2中对比可以看出,硅钢片铁心磁致伸缩沿扎制方向磁致伸缩系数大。
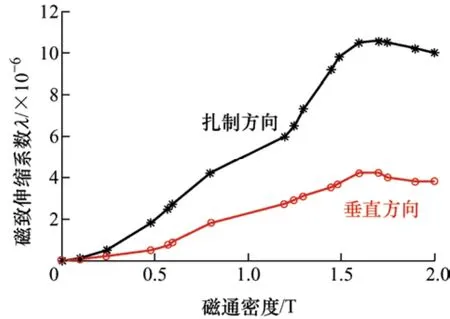
图2 磁致伸缩拟合曲线
根据铁心硅钢片的工作特性,可以得到磁致伸缩系数和磁化强度M的关系[3]
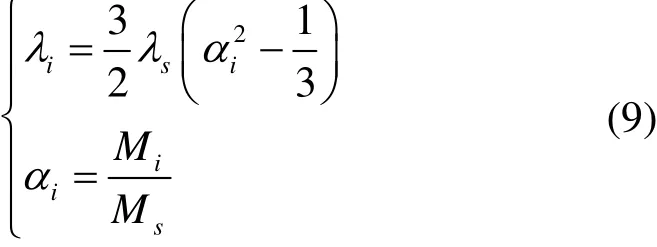
式中,λi与Mi分别表示各个方向的磁致伸缩系数以及各个方向上的磁化强度;λs与Ms分别为磁饱和状态下的磁致伸缩系数以及该铁磁材料磁饱和时的磁化强度,修正系数1/3为未被磁化时的随机去向。若铁心在磁化过程中磁矩与磁化方向垂直,则λi可简化为

2.3 铁心结构力学分析
因变压器铁心结构的限制,铁心各部位磁通密度分布不均,无法由材料的特性模型构建精确、完整的变压器铁心振动数学分析模型。因此,下面依照铁心结构,将铁心按照铁心柱、铁轭两个部件进行分析。铁心柱振动的等效模型如图3a所示,将铁心柱等效为一连续的弹性杆体,图3中y轴方向代表铁心柱轴向(本文约定为竖直方向)的位置。在磁致伸缩的作用下,铁心柱将受到竖直方向上的应力,铁心柱中的每个质量单元都将由初始位置y0开始,发生位移。借鉴结构力学中的机械振动方程,由铁心柱部分受力分析可得到铁心柱振动的力学过程为
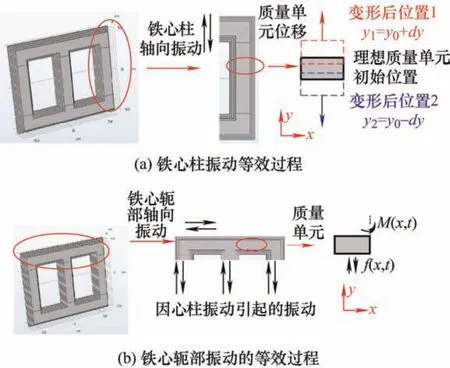
图3 铁心振动过程等效分析模型

式中,e为硅钢片的弹性模量;u为轴向位移;f(y,t)为磁致伸缩作用在每个质量单元y轴方向上的等效作用力;ρ为硅钢片密度;s为质量单元的横截面积。
铁心轭部将因受到铁心柱振动产生的作用力而产生y轴方向上的振动。铁心轭部振动的示意图如图4所示。容易知道,铁轭在x轴方向振动的力学过程与铁心柱在y轴上振动的力学过程有类似的表达

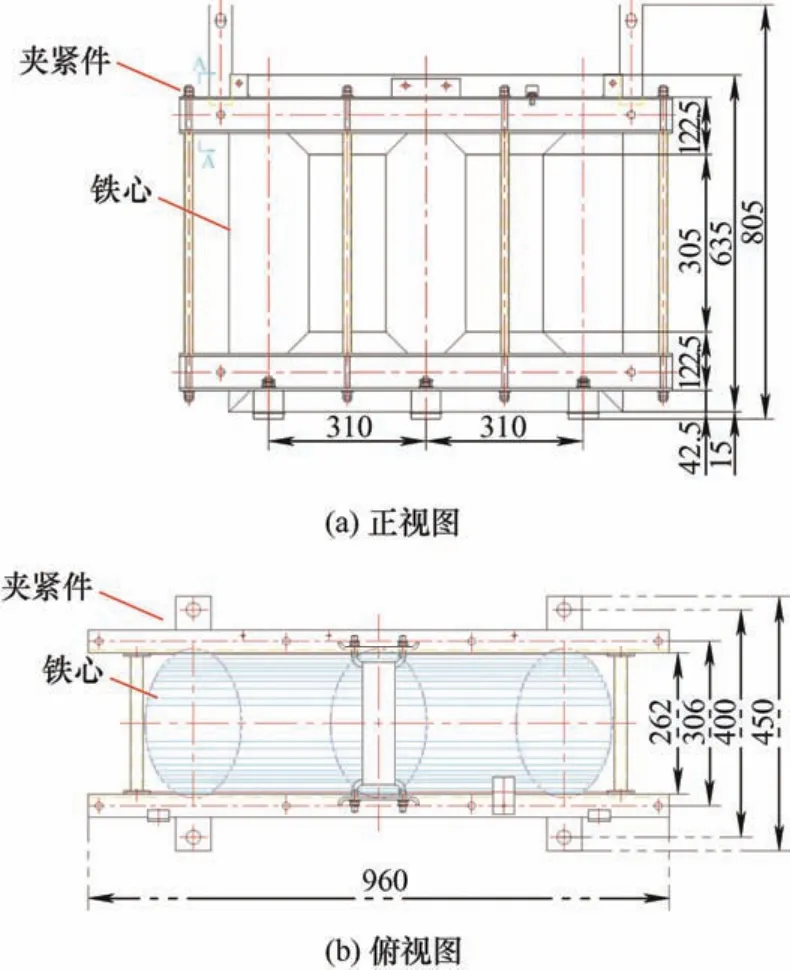
图4 配电变压装配图(mm)
在铁心轭部自激振动、铁心柱自激振动、硅钢片间电磁力以及铁心固定件预紧力的共同作用下,铁轭将会产生如图3b中M(x,t)所示的弯矩,表达式如下所示[3]
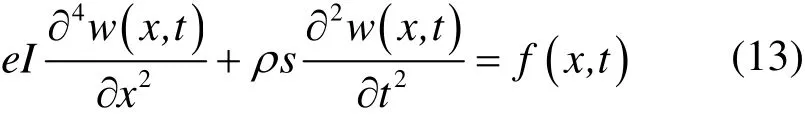
式中,I为轭部的转动惯量;w(x,t)为轭部在x轴方向上的位移;f(x,t)为单位长度上的作用力。
3 多物理场仿真模型
3.1 基本假设
对于实际运行的电力变压器,使用环境以及结构件装配工艺均会对铁心振动造成较大影响。本文在进行变压器铁心振动特性的分析过程中对研究对象进行如下假设[21]。
(1) 忽略实际工况中环境温度以及变压器温升变化对绕组内阻、硅钢片磁致伸缩特性的影响。
(2) 认为变压器铁心为一刚性结构的整体,忽略不同变压器厂商因夹紧工艺的差异对硅钢片磁致伸缩特性以及铁心振动特性的影响。
(3) 认为变压器正常运行状态下铁心的机械振动不会使变压器各结构件产生明显的形变,不会发生相对位移。
上述假设条件排除了制造工艺、使用环境、实际工况等因素对变压器铁心振动情况的影响,在简化计算过程的同时仍然能够有效地反映出正常工况下铁心振动的科学规律与变化趋势。
3.2 几何分析模型
S13-M-400/10-NX2型配电变压器装配的正视图与俯视图如图4所示,变压器铁心在竖直方向上通过结构件由上夹紧件与下夹紧件固定,在垂直方向上由螺杆固定。绕组线圈与变压器铁心柱的装配图如图5所示,由图5a可以看出,变压器原边与副边绕组随铁心柱绕制,呈现出椭圆;在图5b中,低压线圈匝数较少、线径较大,分布在靠近铁心柱侧,高压线圈匝数较多、线径较小,分布在外侧。

图5 绕组与铁心装配图
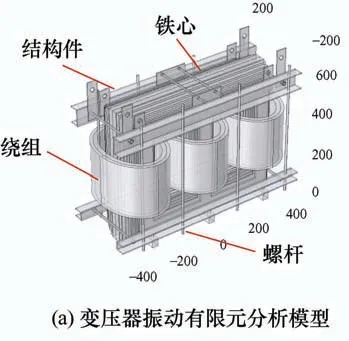
按照以上结构参数对共计63块硅钢片、3个高压线圈绕组、3个低压线圈绕组以及相应的夹紧与固定件进行建模,得到如图6a所示的几何模型。考虑到与变压器铁心相比,夹紧与固定件质量较小,在对变压器进行振动分析的过程中,可以在夹紧件与硅钢片接触面设置相应的预紧力后将夹紧件省略以简化计算模型,简化后的分析模型如图6b所示。将简化后的模型按照空气域、铁心以及线圈分别进行剖分,得到如图6c所示的剖分结果。
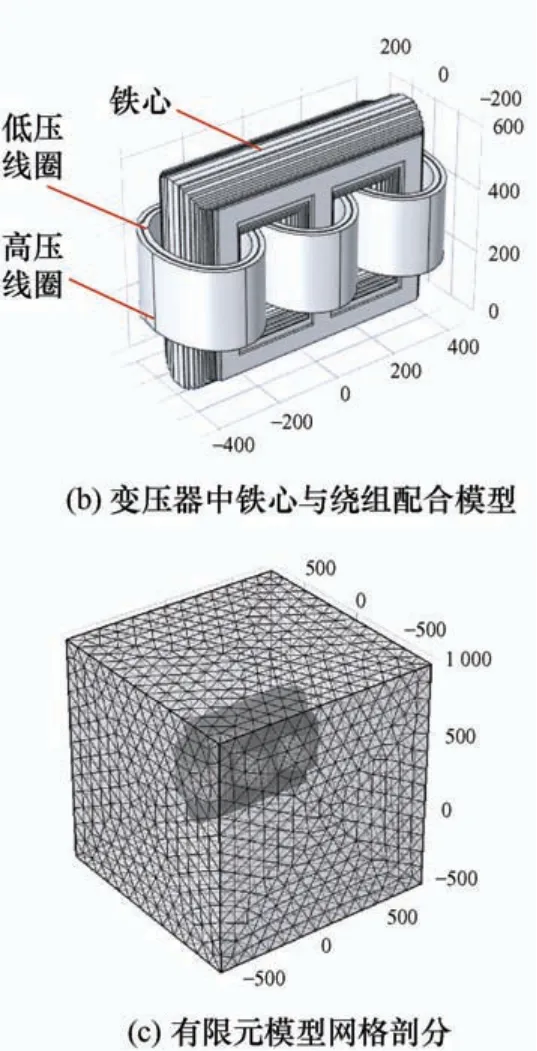
图6 配电变压器振动有限元分析模型(mm)
4 计算结果与分析
4.1 额定工况下振动分析
将变压器高压侧受10 kV,50 Hz三相正弦交流电压激励,输出功率为400 kV·A的工况设置为额定工况,在铁心与夹紧件接触面设置2.6 MPa的预紧力。在COMSOL有限元软件中对模型进行瞬态计算,求解时间范围为0~0.05 s,求解步长设置为2×10−3s,涉及物理场接口包括“电路”、“磁场”以及“固体力学”,多物理场耦合形式为“磁致伸缩”,选择“NUMPS求解器”。
额定工况下变压器不同时刻磁通密度计算结果如图7所示。由图7计算结果可以看出,变压器铁心上窗口内测磁感应强度较高。
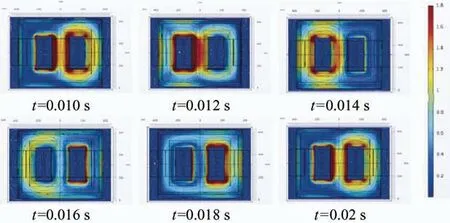
图7 变压器铁心磁通密度分布
变压器铁心应力分布以及放大1.3×105倍之后的形变分布如图8所示,由结果可以看出,窗口内侧应力最大;受到铁心柱和轭部的共同作用,在铁心柱和轭部连接处形变最大。
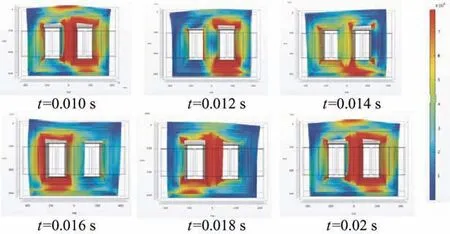
图8 变压器铁心应力及形变分布
如图9所示,在铁心振动分析模型中选取四个分析点,坐标分别为A(0, 0, 350),B(0, 0, 500),C(350,0, 500)以及D(350, 0, 350)。以上述四个分析点为研究对象,对铁心柱以及轭部受力形变情况进行进一步分析。

图9 配变中分析点标注(mm)
由图10中各分析点位移曲线可以看出,四个分析点位移曲线均随原边激励电压变化呈现周期性变化。对比四条位移曲线峰值,可以看出铁心轭部与铁心柱搭接处(图9中所示C点)位移峰值最大,形变最为明显。

图10 分析点位移曲线
4.2 激励电源对振动特性的影响
为分析不同工况下变压器铁心振动变化规律,本节对不同电源激励下变压器位移曲线进行敏感性分析,各分析结果取t=0.01 s时刻。
4.2.1 激励电压幅值对振动特性的影响
定义激励电源电压标幺值如式(14)所示,图11为不同电压幅值激励下A、B、C、D(图9)四个分析点位移曲线计算结果。

式中,U为变压器一次侧激励电压有效值;U0为变压器额定一次侧电压有效值(U0=10 kV)。由图11计算结果可知,各分析点发生的形变随着电压幅值的上升而加剧。
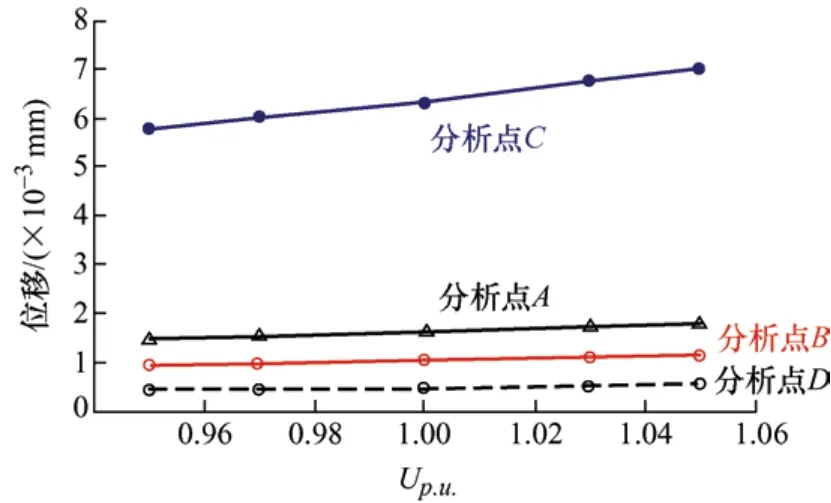
图11 不同电压幅值下铁心位移特性
4.2.2 激励电源频率对振动特性的影响
定义频率标幺值fp.u.如式(15)所示,图12为各分析点在不同一次侧电源频率下位移曲线。
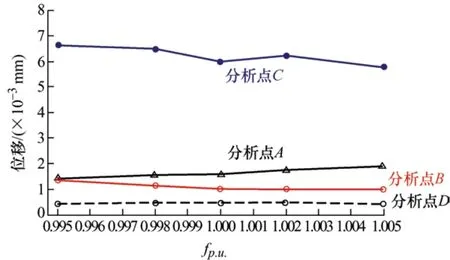
图12 不同电压频率下各分析点位移

式中,f为变压器一次侧电压变化频率;f0为变压器一次侧额定电压频率(f0=50 Hz)。
由图12可以看出,变压器一次侧电源变化频率对变压器形变将产生影响,且形变程度随一次侧电源变化频率增大而减小。
4.2.3 激励电源谐波对变压器振动特性的影响
除上述激励电压幅值、激励电压变化频率外,配电网中谐波含量同样会通过影响变压器铁心中主磁通变化来影响电力变压器的振动特性。由于变压器铁心主磁通受一次侧激励电压影响,本节仅考虑配电网中电压谐波对变压器铁心振动特性的影响。参考国家标准GB/T 14549—1993《电能质量公用电网谐波》,本节在分析过程中对各次谐波含量限制如表2所示,并按式(16)定义一次侧电压的总谐波含量

表2 不同电压等级下谐波电流限制(部分)
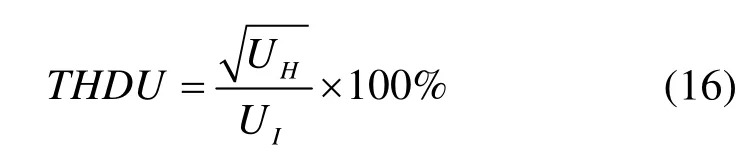
式中,UH与UI分别为变压器一次绕组激励电压各次谐波分量的平方和以及基波含量。鉴于本文研究对象一次侧额定电压为10 kV,变压器激励电压各次谐波最大含量取10 kV计算标准并按式(17)进行取值(假设其他次谐波含量为0%)。

为单独研究各次谐波注入对铁心振动特性的影响,首先在额定工况下标准正弦激励的基础上对激励电源注入各次谐波含量最大值。此时所得位移计算结果可以包含因基波(额定工况下理想正弦激励)产生的位移以及因注入的谐波激励产生的位移两部分。将总位移y0、因基波产生的位移yi以及因注入的谐波产生的位移Δy按叠加原理近似,可以由式(18)得到给次谐波对铁心振动特性的影响。

线性化处理后计算结果如图13所示,变压器形变受三次谐波影响最大,与第2节理论分析结果基本相符,具有一定的通用价值。
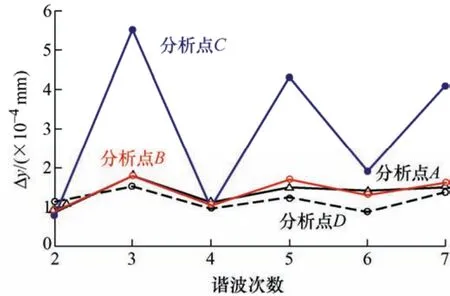
图13 不同次数谐波对铁心振动特性的影响
5 结论
本文针对电力变压器铁心振动特性开展了建模与研究工作,首先分析了变压器铁心电-磁-力耦合机理,随后以某企业生产的S13-M-400/10NX2型号配电变压器为研究对象,建立了电-磁-力多物理场分析模型并针对铁心的振动特性开展了研究工作,得到了以下结论。
(1) 得出了变压器铁心磁通密度、形变与应力分布图,分析应力与形变分布,可以看出在变压器铁心轭部与铁心柱接缝处承受应力最大。
(2) 分析了高压侧激励电压波动对变压器振动特性的影响,发现变压器形变随高压侧激励电源幅值增大而增大。
(3) 分析了高压侧激励电源频率对变压器振动特性的影响,发现变压器形变随高压侧激励电源频率增大而减小。
(4) 分析了电网中各次谐波含量对变压器振动特性的影响,发现三次谐波对变压器振动影响最大,该结果与本文理论分析结果相符,具有一定的通用性,变压器所接线路中应避免三次谐波的含量。
