基于组合赋权和改进灰色关联分析的配电网可靠性影响因素研究

王梦帆 郑建勇 梅 飞

(1. 东南大学电气工程学院 南京 210096；2. 河海大学能源与电气学院 南京 211100)

1 引言

随着科技的不断发展，我国主网构架日益优化，电网供电可靠性逐渐成为电力行业关注的焦点[1-3]。如何对配电网可靠性进行准确、全面的评估，分析影响配电网可靠性的关键因素及其影响程度，对于保障电网供电质量、指导配电网规划改造方向、推进电网智能化发建设都有着重要意义，是近几年电力系统研究中的研究领域之一。

目前，配电网的可靠性评估方法主要有解析法和模拟法两种[4-5]。文献[6]采用解析法中的最小割集法量化评估馈线自动化系统对配电网供电可靠性的影响。文献[7]计及分布式电源和负荷的时变特性，采用分时段方法，并依据贝叶斯网络逻辑关系求解配电网可靠性指标。文献[8]针对传统蒙特卡洛模拟法收敛速度慢的问题，提出一种基于交叉熵蒙特卡洛模拟的含微网配电网可靠性评估方法，提高了计算效率。文献[9]将市场化因素量化引入可靠性评估模型，建立了基于非序贯蒙特卡洛模拟的市场化环境下发输电系统的可靠性评估模型。然而，解析法局限于系统网络拓扑结构，不适合规模较大的系统，而模拟法计算量大、精度低，不利于工程应用[10-12]。

此外，部分配电网拓扑结构不明确或因投入时间较短基础数据有限，不适用上述可靠性评估方法，且传统可靠性评估方法无法快速判断影响配电网可靠性的关键因素及其影响程度。因此部分学者提出了基于数据关联关系分析的可靠性评估方法。这类方法通过相关性分析提取影响配电网可靠性的主要因素，同时挖掘可靠性指标与各影响因素间的关联程度，计算量小，评估速度快，可以有效量化配电网可靠性优劣并且应用于配电网可靠性提升措施优选等。在指标相关性分析方面，文献[13]针对可靠性指标众多且相互关联的问题，提出一种基于变异系数法和聚类分析的可靠性指标体系简化方法，并引入灰色关联分析法进行配电网可靠性评估。文献[14]采用主成分分析法和并行关联规则提取主要指标，筛选影响配电网可靠性的关键因素，减少评估工作量，实现快速精准评估。在关联度分析方面，文献[15]利用故障树分析确定影响用户平均停电时间的多种因素，计算关键因素指标灰色关联度并排序，从而提出针对性的改造措施。文献[16]针对传统灰色关联分析中固定的分辨系数会导致可靠性评估结果趋于平均化的问题，引入分辨系统动态确定方法和模糊加权，改进了基于灰色关联分析的可靠性评估模型。文献[17]建立基于改进熵权的灰色关联分析模型，提高了配电网可靠性评估的客观性。然而，上述研究大多采用客观赋权法，只考虑指标实际的波动情况，忽视了专家对不同指标的重视程度。此外，已有研究大多只针对单一可靠性指标进行影响因素分析，实际上表征配电网供电可靠性的评价指标数目众多，研究关键影响因素对多种可靠性指标合成的综合评价指标的影响是必不可少的。

因此，本文提出一种基于组合赋权和改进灰色关联的配电网可靠性评估及其影响因素分析方法。首先，分别采用G1法和CRITIC法计算各可靠性指标的主、客观权重，构建最小二乘优化模型求解进行合理赋权，合成配电网可靠性综合评价指标。其次，选取与配电网可靠性相关的关键影响因素，采用改进灰色关联分析确定各影响因素相对于可靠性评价指标间的影响程度。引入动态分辨系数克服传统灰色关联中固定分辨系数导致的数据差异性降低问题，并结合TOPSIS方法思想，计算各影响因素与正、负向理想序列的综合灰色关联度。然后以此为依据进行优劣排序，指导配电网可靠性提升措施决策。最后，结合某地区配电网相关数据，验证本文所提方法的有效性。

2 基于G1-CRITIC的组合赋权

配电网的可靠性评估指标数目众多，常用的系统可靠性指标包括系统年平均停电时间SAIDI、系统年平均长时停电频率SAIFI、用户平均缺供电量AENS等[18]。对各影响因素与单一可靠性指标进行关联分析，无法准确评价各因素指标对配电网可靠性的影响程度，进而影响配电网的可靠性评估结果，不利于可靠性提升措施的决策。因此本文针对上述三种可靠性指标，采用基于G1-CRITIC的组合赋权方法，克服单一指标无法全面、真实地反映配电网可靠性水平的问题，形成配电网可靠性综合评价指标，为影响因素关联分析及可靠性评估模型的建立提供基础。

2.1 序关系分析主观赋权法

序关系分析法[19]又称G1法，是一种主观赋权方法。相比于其他几种常用的主观赋权法如专家评分法、层次分析法等，G1法的主要原理是在确定各指标序关系的基础上，对相邻指标的重要程度进行对比，免去了所有指标间两两比较并构造判断矩阵的复杂过程，规避了一致性检验易出错的问题。基于G1法流程简单、计算量小等优势，本文采用G1法为可靠性指标进行主观赋权。

2.1.1 确定序关系假设对某对象，共有m个指标，构成指标集{y1,y2,… ,ym}。在指标集{y1,y2,… ,ym}中，若指标yj相对于yi重要性程度更大，则记为yj>yi。专家根据经验对这m个指标按照如下步骤进行排序，从而确定指标集{y1,y2,… ,ym}的序关系。

(1) 专家在指标集{y1,y2,… ,ym}中选择重要程度最高的指标，记为y1*。

(2) 在剩下的m−1个指标构成的指标集中，选择重要程度最高的指标，记为

(4) 将这m个指标按照的顺序排序，其中则称指标集确立了序关系。

2.1.2 确定重要性标度

式中，jω和ωj1−分别为指标yj与yj−1的权重；hj的取值参考表1。

表1 重要性标度hj取值参考

2.1.3 计算主观权重

根据文献[19]的推导，可知确立了序关系的指标集中各指标的权重为

2.2 CRITIC客观赋权法

CRITIC法[20]是由DIAKOULAKI提出的一种通过计算指标数据中蕴含的信息量来赋权的客观赋权方法，指标信息量越大，相应的权重就越大。作为熵权法的一种改进，CRITIC法同时考虑了指标间的对比强度和冲突性，能够更客观准确地进行赋权。

2.2.1 指标预处理

假设对于某评价目标，共有m个指标，n个评价对象，构成指标矩阵。由于各指标间存在量纲和数量级差异，采用CRITIC法赋权前，应对指标进行标准化处理，从而得到标准化矩阵

对于逆向指标，按照式(4)进行标准化处理

对于正向指标，按照式(5)进行标准化处理

2.2.2 确定标准差及相关系数

CRITIC法通过标准差和相关系数来体现评价指标的对比强度和冲突性，标准化处理后的各指标标准差和相关系数计算公式如下

2.2.3 计算客观权重

以cj表示指标j所包含的信息量

由CRITIC法确定的客观权重计算方法如式(9)所示，记为

2.3 最小二乘法优化模型

序关系分析法具有一定主观局限性，CRITIC法则没有考虑专家对不同指标的重视程度，因此本文以组合权重对应的综合评价值与主客观权重对应的评价值偏差最小为目标函数，建立最小二乘法优化模型如式(10)所示，实现主客观统一。

3 基于改进灰色关联的影响因素分析

考虑到与配电网可靠性相关的影响因素指标数目众多，需要对其进行筛选，选出与可靠性相关性强的核心影响因素指标，减少复杂度和计算量。本文构建影响因素指标体系如图1所示。

图1 配电网可靠性影响因素指标体系

为量化和判定各影响因素对可靠性的影响程度差异，本文通过改进灰色关联分析，计算各影响因素与可靠性指标的关联度并进行排序，进而从可靠性提升角度，对配电网的改造方向提供参考。

3.1 灰色关联分析基本原理

灰色关联分析[13]的核心思想是通过比较各因素序列曲线在变化势态、方向、大小等方面的相似程度，判断各因素序列间的关联程度。在考虑影响因素关联关系的配电网可靠性评估问题中，以可靠性指标序列作为正向理想序列，并计算各影响因素序列与正向理想序列的灰色关联度，灰色关联度越大，表示该影响因素相对于配电网可靠性的重要程度越大。关联度计算步骤如下。

(1) 确定评价矩阵。假设参与可靠性评估的配电网数量为n，以可靠性综合评价指标作为正向理想序列，记为与可靠性相关的影响因素序列记为假设影响因素有m个，则可以确定原始评价矩阵X。

各影响因素指标间存在量纲和数量级差异，因此采用式(13)对各影响因素序列进行无量纲化处理。

考虑到可能存在影响因素序列与可靠性评估指标变化趋势相反的情况，对于这类影响因素序列，应在无量纲化处理后取倒数，使其变化势态与可靠性指标一致，避免产生关联度计算偏小的问题，最终得到评价矩阵

(2) 计算关联系数。第i个可靠性影响因素的第j个数的关联系数ijβ计算公式如下

式中，ε为分辨系数，其范围为0～1，通常取0.5。(3) 确定关联度。第i个可靠性影响因素与可靠性综合评价指标序列X0的整体灰色关联度为

3.2 改进灰色关联分析

传统灰色关联分析存在一定局限性，只能分析不同待评价序列中相同因素间的关联性，且通常在计算关联度时固定分辨系数为0.5，不能很好地体现数据间的差异性，所以时常出现与实际情况不符的结果。本文引入动态分辨系数和TOPSIS法对其进行改进。

3.2.1 动态分辨系数

由式(14)可知，关联系数ijβ的计算结果与ε的取值以及各影响因素序列波动性有关。当影响因素序列波动性较小时，Δmax和ijΔ的数值较接近，若ε取0.5则会导致关联系数数值较小且分布十分接近，当影响因素序列波动较大时，Δmax远大于ijΔ和Δmin，若此时仍取ε为0.5，则式(14)的分母完全由ε决定，忽略了ijΔ的作用，且最终计算出的关联系数都接近于1。

因此本文引入判断系数εΔi表征各影响因素序列的波动性

以0.5为分界值，当判断系数εΔi＞ 0 .5时，说明影响因素序列较平稳，取任意ε∈[ 0.8,1]，均可增强关联度间的差异性；当εΔi＜0 .5时，说明影响因素序列波动较大，此时ε应取较小值来减少Δmax对计算结果的影响，本文中取

3.2.2 结合TOPSIS思想的灰色关联分析

灰色关联分析中的灰色关联度，可以看成待评价序列与正向理想序列的距离，灰色关联分析的核心思想就可以理解为通过比较不同待评价序列与正向理想序列的距离进行优劣评价。然而如图2所示，当待评价序列Xi、Xj相对于正向理想序列X0距离相同时，无法在Xi、Xj间进行优劣判断。引入TOPSIS方法思想，设负向理想序列为，则可以通过观察Xi、Xj相对于的距离，作出Xi优于Xj的判断。

图2 结合TOPSIS思想的综合灰色关联度示意图

将这种思想引入灰色关联分析，则第i个可靠性影响因素与负向理想序列的整体灰色关联度为从而通过综合灰色关联度iψ表征各影响因素对配电网可靠性的影响程度。

3.3 整体流程

本文基于可靠性综合评价指标与各影响因素之间的关联分析，建立可靠性评估及其影响因素分析模型，整体算法流程如图3所示。

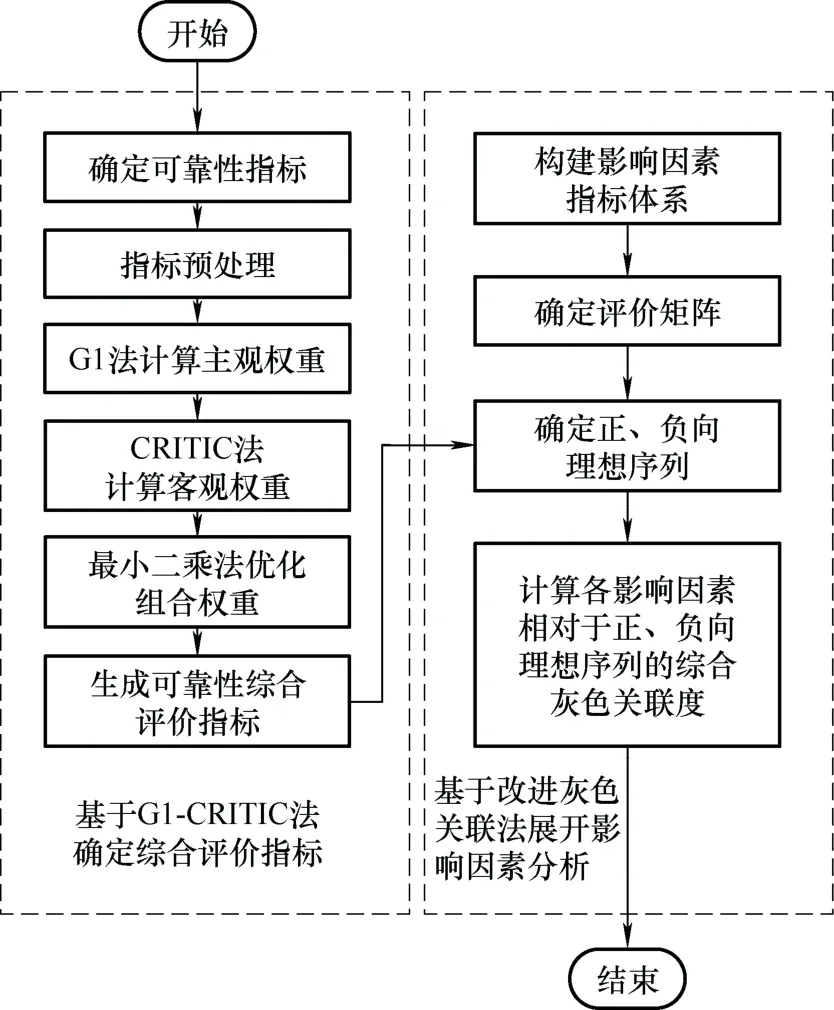
图3 可靠性评估及其影响因素分析流程图

4 算例分析

为了验证本文所提方法的有效性和可行性，以某地区8个配电网为例进行分析。可靠性指标具体数据如表2所示。

表2 各配电网可靠性指标数据

根据第3节构造的影响因素指标体系可知，本文共选取X1～X9共9种影响因素指标。各配电网可靠性影响因素指标数据如表3所示。

表3 各配电网可靠性影响因素指标数据

4.1 可靠性综合评价指标合成

运用序关系分析法，根据专家经验确定可靠性指标的序关系，参考表1确定相邻指标间的重要性标度，最终求得SAIDI、SAIFI、AENS的主观权重为W1=[0.17, 0.53, 0.30]。

运用CRITIC法进行客观赋权，根据式(6)～(10)计算得到各指标客观权重：W2=[0.48, 0.33, 0.19]。

由此可见，CRITIC法的赋权结果与序关系分析法相比差异明显，脱离了实际经验，而只采用序关系分析法的赋权结果又忽视了数据自身包含的信息。因此采用基于最小二乘优化模型的组合赋权法，结合序关系分析法和CRITIC法的优点，在考虑数据本身信息量和相关性的同时，兼顾了专家经验，为各可靠性指标合理赋权。模型采用遗传算法求解得到各指标的组合权重：W=[0.30, 0.44, 0.26]。

根据式(11)计算各配电网可靠性综合评价指标X0=[0.782 5, 0.669 2, 0.753 1, 0.732 1, 0.796 8,0.863 5, 0.801 7, 0.886 8]。按照各配电网可靠性综合评价指标值对配电网进行可靠性排序，即配电网8＞配电网6＞配电网7＞配电网5＞配电网1＞配电网3＞配电网4＞配电网2。因此可以得到该地区中配电网8的可靠性最好，而配电网2的可靠性最差的结论。针对可靠性较差的配电网，接下来将通过影响因素关联性分析，为配电网提升可靠性提供参考。

4.2 影响因素关联性分析

对各影响因素指标数据按第3.1节所述方法进行相应处理后得到评价矩阵设置正向理想序列为X0，负向理想序列为

引入动态分辨系数调整策略，根据式(14)～(21)分别计算影响因素指标序列与正、负向理想序列的灰色关联度，最终得到各影响因素指标的综合灰色关联度iψ=[0.825 7, 0.849 8, 0.861 1, 0.836 5,0.412 3, 0.907 1, 0.601 2, 0.943 6, 0.865 8]，从而得到各影响因素相对于配电网可靠性的影响程度排序：

可以得出以下结论：配电自动化水平对该地区配电网可靠性影响程度最高，而配电变压器平均复杂率的影响程度最低。因此，加强配电网自动化建设，提高配电网自动化水平是提升该地区配电网可靠性的最有效措施，而与配电变压器平均负载率相关的各项措施则提升效益相对较低。因此针对该地区内可靠性最低的配电网2，采取提升配网自动化水平的相应措施可以最有效改善其可靠性。

为了进一步验证本文所提方法的有效性和准确性，采用不同方法对影响因素进行关联性分析作为对比，分别为① 仅对SAIDI作影响因素关联性分析；② 仅对SAIFI作影响因素关联性分析；③ 仅对AENS作影响因素关联性分析；④ 采用TOPSIS与传统灰色关联分析相结合的方法对综合评价指标作影响因素关联性分析；⑤ 采用引入动态分辨系数调整策略的灰色关联分析方法，对综合评价指标作影响因素关联性分析。计算结果如表4所示。

表4 多种关联性分析方法结果

观察上述5种方法和本文所提方法求得的影响因素关联度，发现无论采用哪种方法，配电自动化水平X8和中压电网平均故障修复时间X9的关联度都较大，而配电变压器平均负载率X5和带电作业指标X7的关联度则在这几种计算方法所求的结果中普遍较小，证明了本文所提方法与传统方法的计算结果具有一定程度上的一致性，本文所提方法是合理可信的。

方法1得到的影响因素排序为X1＞X8＞X9＞X6＞X3＞X5＞X2＞X4＞X7，方法2得到的影响因素排序为X8＞X9＞X6＞X3＞X2＞X4＞X1＞X7＞X5，方法3得到的影响因素排序为X3＞X9＞X4＞X8＞X6＞X2＞X1＞X5＞X7。以上三种排序差异较大，可见采用单一可靠性评价指标不利于准确分析影响因素与可靠性间的关联关系，进而影响配电网可靠性提升决策。而本文采用G1-CRITIC法对多项可靠性指标组合赋权，合成可靠性综合评价指标，既可以用来检验前期规划成效，又能为后续配电网改造升级提供较为全面的指导。

采用方法4时，关联度较大(＞0.7)的数据分布范围较小，影响因素关联度序列方差为0.026 9。而采用本文方法时，关联度较大(＞0.7)的影响因素关联度序列方差为0.071 4。可以看出本文采用的分辨系数动态赋值方法，增强了各影响因素关联度间的差异性，验证了本文所提方法的有效性。

方法5得到的影响因素关联度计算结果中X6关联度与X8关联度几乎一致，在配电网可靠性提升措施优选中难以对他们进行抉择。而本文所用方法结合了TOPSIS思想，计算结果中X6关联度与X8关联度的差距明显增加，从而可以对这两个影响因素进行优劣区分，弥补了方法5的不足。

5 结论

本文提出了一种结合了基于G1-CRITIC法的综合指标权重计算和改进灰色关联的配电网可靠性评估及其影响因素分析方法，结论如下。

(1) 相比于常规可靠性评估研究，本文所提方法不局限于网络拓扑结构，计算速度快，计算量小，且可以快速分析各影响因素对配网可靠性的影响程度。

(2) 采用基于最小二乘的G1-CRITIC法计算组合权重，合成可靠性综合评价指标，对区域内各配电网可靠性进行综合评价，使各影响因素对配网可靠性的影响程度分析更为全面。

(3) 采用动态分辨系数改进传统灰色关联分析法，突出影响因素间的差异性，能够更有效地识别出对可靠性影响较大的因素。

(4) 引入TOPSIS方法思想，弥补了无法对两关联度相近的影响因素进行抉择的问题，可以为配电网可靠性提升措施优选提供更准确的指导。