多变换器系统无源控制策略研究*

2022-05-20王振业王久和张梦壕

电气工程学报 2022年1期

王振业王久和张梦壕

(北京信息科技大学自动化学院北京 100192)

1 引言

随着电力电子技术的发展，多变换器系统(Multi-converter system，MCS)已经广泛应用在直流微电网、工业制造、国防科技、电网配送电以及新能源发电等领域[1]。在能源短缺以及环境问题日益严重的大背景下，包含MCS系统的直流微电网得到了广泛关注[2]。同时，直流微电网具有成本低、变换环节少、损耗较低等优点，且不存在无功、相位等问题，具有广泛的应用前景[3-4]。

电力电子变换器在系统中是实现能量传递与转换的主要功率处理单元，它们之间的相互作用会引起功率振荡进而影响系统的稳定性[5]。同时，闭环控制下的电力电子变换器在输入端会呈现恒功率负载特性。恒功率负载(Constant power load，CPL)具有负阻特性，其在MCS中的比例越来越大也会对系统的稳定性产生不利影响[6]。因此，如何维持MCS的稳定高效运行是值得进一步探究的问题。

直流微电网系统中包含多个电力电子变换器，学者们对其进行整体建模并进行了大量的研究分析。但是由于分布式能源的灵活性和不确定性，MCS可能具有时变的系统结构和运行方式。这一特性对传统的基于固定和完整系统模型的稳定性分析方法提出了挑战[7]。

ORTEGA等[8]提出的无源控制(Passivity based control, PBC)从能量角度分析问题并进行控制器设计，为非线性控制提供了有效的方案。由无源控制理论可知：若系统是无源的，则系统是稳定的；若系统由多个无源子系统构成，则系统仍然是无源的，亦为稳定的[9]；这为多变换器系统的稳定性问题提供了有效的方案。文献[10-11]基于无源控制理论提出了自律稳定控制策略，即通过保证每个变换器的无源稳定性达到整个系统稳定的目的。自律稳定控制策略有效避免了对系统的整体建模，同时论证了无源控制分散致稳的可行性，但是该策略是基于小信号模型下的分析和设计。尽管小信号分析是简单可行的，但是局部线性化的模型只在一个稳定点的附近是正确的，在系统受到大扰动时并不适用。

本文采用无源控制分散致稳的思想，基于欧拉-拉格朗日(Euler-Lagrange, EL)模型，结合自抗扰控制技术，提出一种多变换器系统无源控制策略。将MCS分为若干个子系统，将致稳的责任分散到各个子系统，通过子系统的无源稳定来保证MCS的稳定性。通过大信号稳定性分析，不仅可以保证期望点附近稳定可控，还可以保证系统受到大扰动时的全局稳定可控。在Matlab/Simulink搭建的MCS仿真模型下，与PI结合无源控制相比，本文提出的控制策略使得直流母线电压得到了更好的控制，系统具有更好的鲁棒性和灵活性，进而验证了控制策略的可行性与优越性。

2 系统结构和分散致稳控制策略

2.1 系统结构

MCS在直流微电网系统中有着广泛的应用，本文以直流微电网系统为例对多变换器系统进行研究。MCS系统结构图如图1所示，该系统中包含了多个电力电子变换器。系统中能量的传输与母线电压的稳定都离不开变换器的控制。分布式电源等装置给负载供电时，需要通过变换器接入直流母线；交流电网和部分负载也需要通过变换器才能从系统中吸收能量。

图1 MCS结构图

为了避免对系统的复杂的整体建模，本文采用无源控制理论，以变换器为核心将系统划分多个不同子系统，子系统结构图如图2所示。

图2 MCS子系统结构图

2.2 分散致稳控制策略

分散致稳控制策略以无源控制为基础，通过各分散子系统的无源稳定来保证互联大系统的稳定。无源控制理论着重于从系统的能量方面来研究系统的稳定和控制问题。从根本上来说，系统无源性的物理背景和无源性定义与Lyapunov稳定性函数有一定的联系[12]。实际系统中各物理量都在发生变化，从能量的角度来看，控制了系统的能量变化即控制了系统的物理量，进而可以实现系统的稳定[13]。

如果一个系统存在连续可微半正定的存储函数H(x(t))，并满足耗散不等式，即

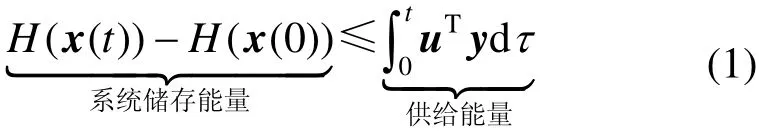
或

则系统是无源的。式中，x(t)表示系统的状态变量；u是系统的输入，y是系统的输出；uTy是供给率，反映流入系统能量的速率。

若存在正定函数Q(x)且满足

或

则系统是严格无源的。无源控制理论还指出多个无源系统通过并联或者反馈连接结合在一起得到的系统也是无源的，这一结论可以推广到任意数目互联的无源子系统[11]。

在实际系统中，任何线性的RLC网络无论其多么复杂，总是无源且稳定的。因此，无源控制理论适用于研究复杂的、由多个非线性电力电子变换器组成的多变换器系统。它可以将大系统的稳定性问题转化到分散的子系统变换器层面。通过相互连接的子系统的能量变化来确定整个系统的行为。

本文以boost变换器和buck变换器组成的简易系统为例来研究MCS，其结构图如图3所示。

图3 简易MCS结构图

该MCS由三个子系统组成。若子系统A、B、C都是严格无源的，设此时三个子系统的储存函数分别为H1(x)、H2(x)、H3(x)，且其组成的大系统的储存函数为H(x)。

结合式(4)可得

式中，Q1(x)、Q2(x)和Q3(x)都为正定函数。

由式(5)可得

由式(6)可以看出，互联之后的大系统依然满足耗散不等式，依然是无源的；即使负载子系统B或负载子系统C被切除，以及增加新的无源子系统，互联系统仍然是无源的，这一结论为系统的灵活性提供了理论支持，同时这一结论可以推广到任意数目互联的无源子系统。

3 系统建模与控制策略

3.1 系统建模

MCS拓扑结构图如图4所示。系统中包含boost源变换器、buck负载变换器和boost负载变换器。电源通过boost源变换器升压与直流母线相接，负载通过负载变换器从直流母线上汲取能量。其中ibo和ubo分别是电源的输出电流和电压；Lbo和Cbo分别是boost源变换器电感器的电感和电容器的电容，T1是boost源变换器的开关管；ipo和uDC分别是boost源变换器的输出电流和直流母线电压。Lbi和Cbi分别是boost负载变换器电感器的电感和电容器的电容，T3是boost负载变换器的开关管；ilo2是boost负载变换器的输出电流；uload1和ib分别是boost负载变换器电容器两段电压和流过电感器的电流。Lbu和Cbu分别是buck负载变换器电感器的电感和电容器的电容；uload2和ibu分别是buck变换器的电容器两端电压和流经电感器的电流；ilo2是buck变换器的输出电流。T2是buck负载变换器的开关管，开关S1控制负载的并入。

图4 MCS拓扑结构图

设电源侧boost源变换器子系统输出侧的等效恒功率为PCPL，开关管T1的控制信号的占空比为d。在连续导通模式(Continuous conduction mode, CCM)下，选择电感电流ibo和电容电压uDC作为状态变量，即x=[x1x2]T=[ibouDC]T。根据图4所示结构图，由基尔霍夫定律可得

将式(7)改写为EL模型形式，即

显然Jbo=-Jbo为反对称矩阵，所以式(8)具有EL方程属性。

3.2 无源性分析和无源控制器设计

设系统的存储函数为

则有

令y=x，Q(x)=xTRbox，由式(4)可得系统是严格无源的，可以进行无源控制器设计。

设状态变量x=[x1x2]T=[ibouDC]T的期望平衡点为则误差变量可设为xe=x-x*，误差能量存储函数则为

无源控制器从能量角度入手，通过能量成型及阻尼注入方法使误差能量函数He(x)加速收敛到0来达到xe→0(即)的控制目的。将xe代入式(8)，同时在等式两边加入阻尼耗散项Rboaxe使误差能量函数He(x)更快收敛到0，可得

可得误差能量函数对时间的导数为

并且式(14)小于0恒成立，故可取无源控制律为

将式(15)展开可得

由式(16)可得boost源变换器开关T1控制信号的占空比为

由式(17)可知，d2选择合适的阻尼注入ra2可以使电压uDC快速收敛到期望值但实际上uDC的上升依赖于电源侧的供给，即在ibo没有快速上升的情况下，uDC很难快速到达期望值，所以选择d1作为开关管T1开关信号的占空比，式中的由外环的自抗扰控制器提供。

依据以上步骤可以得到buck变换器开关T2控制信号的占空比为

结合式(4)和式(10)可知，Rbo恒大于0，电感电流取任何正值都不会影响系统的无源性，自抗扰控制器提供电流期望值，自然也不会影响系统的无源性。结合经典稳定性分析方法Lyapunov第二定律可以对所设计的控制器进行稳定性分析选择He(x)为Lyapunov函数，结合式(13)、式(14)和式(17)，可得He(x)的导数为式中，Rbo和Rboa都大于0，只有在系统达到平衡状态，即xe=0时，等号才成立，所以无源控制器能够达到控制效果并且是稳定的[14]。

3.3 自抗扰控制器设计

自抗扰控制器一般由非线性跟踪微分器(Tracking differentiator, TD)、扩张状态观测器(Extended state observer, ESO)和非线性状态误差反馈(Nonlinear state error feedback, NLSEF)三部分构成[15]。由于电流可通过测量直接获得，为减小设计难度，省略TD和ESO环节[16]。简化后的自抗扰控制框图如图5所示。

图5 简化后的自抗扰控制框图

由boost源变换器两端的功率平衡可得

将式(20)整理成自抗扰控制器设计所需的标准形式为

引入典型的非线性函数fal函数

可得误差反馈控制律为

式中，e=(uDC*-uDC)；参数的选择可以依据以下原则：β为可调参数；α为0～1的常数，α越小跟踪越快，但是滤波效果会变差；δ为影响滤波效果的常数，其越大滤波效果越好，但是会增加跟踪的延时。

按照以上步骤也可以求得buck变换器的误差反馈控制律为

进而可得MCS的总控制框图，如图6所示。

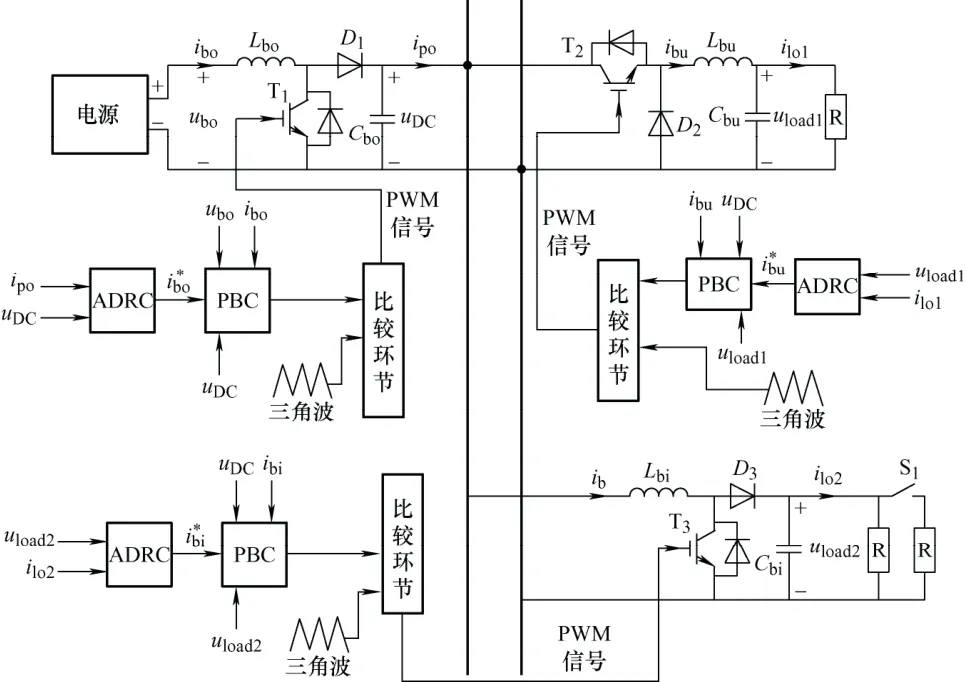
图6 MCS总控制框图

4 仿真研究

根据图4所示MCS拓扑结构图，利用Matlab/Simulink搭建仿真模型，系统参数如表1所示。根据上文提到的参数选择原则，选择控制器参数如表2所示。电压和电流的采样由Simulink中的电压和电流测量模块实现。为了验证该控制策略的控制效果，设置多个扰动对系统进行仿真研究。

表1 系统参数

表2 控制器参数

1 s时boost负载子系统接入并联电阻，PCPL由750 W变为1 000 W；2 s时boost负载子系统切除并联电阻，PCPL由1 000 W变为750 W；4 s时，将buck负载子系统切除，PCPL由750 W变为250 W；5 s时，将buck负载子系统重新接入。仿真结果如图7、图8所示。

图7 恒功率负载变化时的直流母线电压

图8 恒功率负载变化时的boost源变换器电感电流

保持多变换器系统PCPL为1 000 W的情况下，在0.5 s时，电源电压由100 V升高到120 V，1 s时恢复到100 V；1.5 s时电源电压跌落到80 V，2 s时恢复到100 V；电源电压变化时系统的动态响应如图9、图10所示。

图9 电源电压变化时的直流母线电压

图10 电源电压变化时的boost源变换器电感电流

根据系统面临不同扰动时的仿真结果可以得到直流母线电压响应指标，如表3所示。与PI结合无源控制相比，本文提出的控制策略解决了快速性与超调的矛盾，使得系统具有更好的动态和稳态性能，在恒功率负载变化以及电源电压变化时具有更好的鲁棒性。同时，在对buck负载子系统进行切除和重新接入操作时，直流母线电压的表现说明系统具有即插即用的灵活性。