二分法在非对称区间积分中的应用*

刘志高

(马鞍山职业技术学院基础部，安徽 马鞍山 243031)

引言

定积分是积分学的一个基本概念， 许多理论和实际问题都归结为计算定积分的问题．牛顿—莱布尼茨公式是计算定积分的最核心最基本的公式， 需要先求出被积函数的原函数，然后代入公式计算出定积分的值．求原函数的常规方法是换元积分法和分部积分法，它们都是从被积函数的特征出发，考虑通过各种变换将复杂的被积函数转化为简单的被积函数，从而达到求出原函数的目的．但对于原函数不易求出或者原函数无法用初等函数表示的被积函数来说，它们就显得山穷水尽了．如果我们换个角度，从积分区间入手，结合被积函数的特征，通过变换来简化积分运算，往往会柳暗花明．文献[1]利用积分区间和积分区域的对称性以及被积函数奇偶性大大简化了定积分和二重积分的计算．文献[2]给出了若干类非奇非偶函数在对称区间上积分的简化计算．文献[3]给出了对称区间上一类含有指数函数的积分公式，提供了若干国内外数学竞赛试题的一种统一解法．实际计算定积分时，常常会遇到积分区间不是对称区间且被积函数不具有奇偶性的情形．文献[4]利用RMI原理将非对称区间上的定积分转化为对称区间上的定积分，从而简化了定积分的计算．文献[5]针对一些原函数不易求出的定积分，通过强化或弱化前提条件，给出了若干类便于计算的通用公式，简化了任意函数在非对称区间上积分的计算．

二分法也叫折半法，广泛应用于数学和计算机领域．如二分法求方程的近似根、二分法查找有序数组中的特定元素等等．

本文利用二分法将非对称区间上的定积分转化为该区间一半上的定积分，再结合被积函数的某些特点，简化定积分的计算．

1 非对称区间积分的计算公式

定理1设函数f(x)在[a,b]上连续，则有

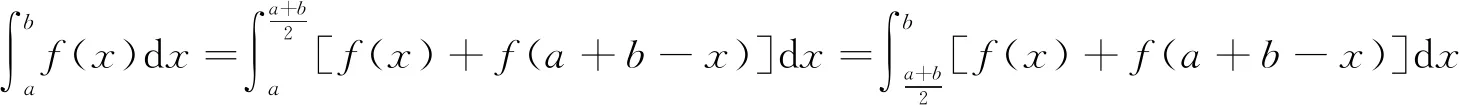
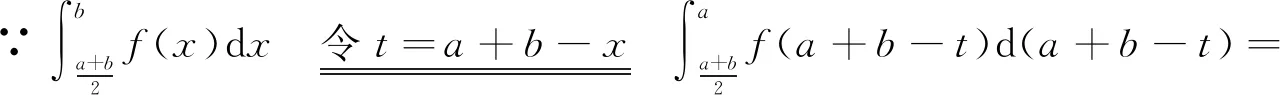
注1 定理1将f(x)在非对称区间[a,b]上的定积分转化为f(x)+f(a+b-x)在该区间一半上的定积分，当f(x)+f(a+b-x)的定积分容易求时，利用上述公式计算定积分非常简便有效．

注2 对于任意有限区间[a,b]，在通常意义下，它不一定是对称区间，但以二分法观点看，它可看作关于区间中点对称的区间．

利用定理1很容易得到对称区间上定积分的一些性质：

推论1 设函数f(x)在[-a,a]上连续，则有

推论2 设函数f(x)在[-a,a]上连续，则有

利用定理1还可以得到以0为左端点的非对称区间上定积分的一些性质：

推论3 设函数f(x)在[0,2a]上连续，则有

推论4 设函数f(x)在[0,1]上连续，则有

2 应用举例

2.1 计算定积分

解 由推论4得，

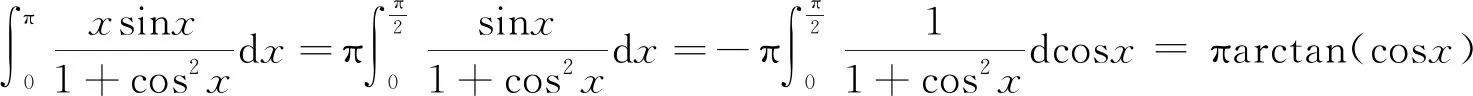
例1是以0为左端点的非对称区间上的定积分，可以用推论4解决．如果是一般的非对称区间上的定积分，则需要用定理1解决．

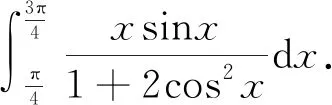
解 由定理1得，

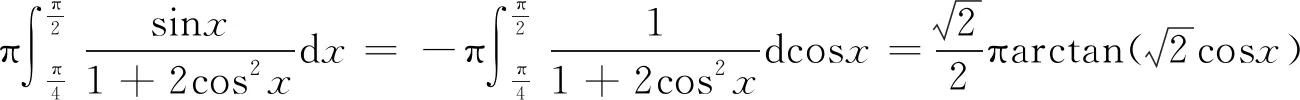
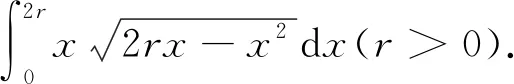
解 由定理1得，

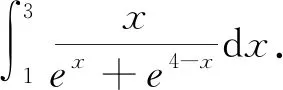
解 由定理1得，

解 由定理1得，

一般地，有如下结论：

解 由定理1得，

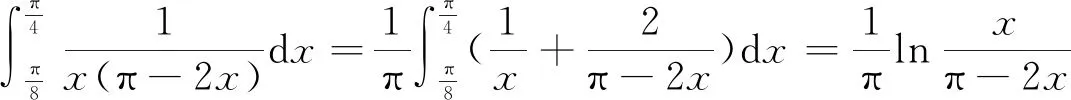
2.2 证明积分恒等式

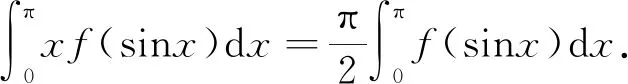
证明 由定理1得，

2.3 证明积分不等式

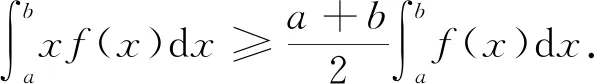
证明 由定理1得，

其中ξ在x与a+b-x之间，

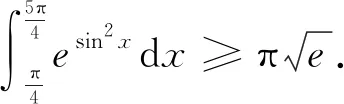
证明 由定理1得，

3 结语

二分法原理为我们解决实际问题提供了一个非常重要的思维方法，在数学中有着极其广泛的应用．对于原函数不易求出或者原函数无法用初等函数表示的被积函数，常规思路往往计算过程比较繁琐，缺乏灵活性和创造性．若能使用二分法，则可将复杂问题简单化，达到事半功倍的效果．

本文利用二分法将f(x)在非对称区间[a,b]上的定积分转化为f(x)+f(a+b-x)在该区间一半上的定积分，通过几个应用实例说明该公式具有一定的普适性和简捷性，不失为计算定积分的一种有效便捷的方法．