基于潮流分布矩阵的电力系统碳排放流计算方法
2022-05-19汪超群陈懿迟长云陶媛李晓波蒋雪冬
汪超群, 陈懿*, 迟长云, 陶媛, 李晓波, 蒋雪冬
(1.浙江浙达能源科技有限公司, 杭州 310012; 2.浙达电力科技(杭州)有限公司, 杭州 310012;3.浙江大学电气工程学院, 杭州 310007)
随着能源危机与气候变化问题的日益突出,世界各国逐步形成了发展清洁可再生能源、减少化石燃料过度消耗、实现低碳可持续发展的重要共识[1]。围绕该共识,中国政府率先提出了2030年“碳达峰”、2060年“碳中和”的宏伟目标[2-3],为全球气候治理树立了积极正面的形象。
“双碳”目标的提出,预示着在今后相当长一段时间内中国的节能减排工作将处于至关重要的地位。与此同时,各行各业尤其是电力行业,将肩负起产业结构调整与转型的重大历史使命。据有关资料统计,电力生产一直是中国碳排放的主要来源之一,其二氧化碳排放量约占全社会碳排放总量的50%[4],面临着前所未有的减碳压力。为了实现电力低碳发展,开展碳排放的分析与统计工作尤为重要。目前,电力系统碳排放计算主要有宏观统计法[5-6]和碳流分析法[7-8]。其中,宏观统计法从宏观数据出发,根据能源消耗总量进行统计,具有计算简单、使用方便等优点。但是该方法的计算结果过于粗放,无法追踪碳排放具体流向,不利于碳排放责任划分与认定。而碳流分析法通常与潮流分析相结合,通过引入节点碳势、碳流率、排放强度等概念实现碳排放具体流向的准确跟踪和定位。相较于宏观统计法,碳流分析法不仅可以精准获取系统的总体碳排放,而且还能够将发电厂的排放公平分摊到各节点负荷和各支路功率,从而极大推动了电力系统碳流分析理论[9-12]的发展和进步。
文献[13]结合网络分析技术,提出了有关碳排放计算的关键指标和概念,初步建立了碳流分析理论的基本体系和框架,为电力系统碳排放计算带来了新的思路和手段。文献[14]在文献[13]的基础上,进一步剖析了碳排放流与潮流的联系,在忽略网损的情况下,提出了电力系统碳排放流的基本计算方法。文献[15]通过定义3种关联矩阵,将发电机组的注入碳流与节点和支路的碳流对应,揭示了碳排放流在电力网络中的分布特性和传输消费机理。考虑到文献[13-15]中的方法均建立在无损网络的基础上,无法适用于实际有损网络的情形。为此,文献[16]将网损分摊到负荷,通过计算线路等效传输功率和节点等效负荷,将有损网络转化为无损网络,从而在一定程度上弥补了碳流分析理论的不足。虽然文献[16]扩展了碳流分析理论的适用范围,使其能够适用于实际有损网络的计算。但是其在计算过程中仍旧对网络损耗做了假设和近似,即认为线路损耗相对于传输功率占比很小,该假设意味着碳流计算的准确性仍有进一步提升的空间。
鉴于此,提出一种计及网损的电力系统精准碳排放流计算方法,以交流潮流计算结果为输入,基于比例分配原则,构造潮流分布矩阵,将发电机有功准确分解到各节点负荷、各支路功率以及网络损耗;然后结合不同发电机的实时碳排率模型,以及网络中的功率分布,利用碳排放流依附于有功潮流的特征,实现电力系统碳排放的公平、合理分摊。最后,以4节点和30节点系统为例,计算对应网络中的碳流分布,分析其合理性,并验证该方法的有效性。
1 电网功率分布
1.1 交流潮流计算
电力系统的碳排放流与功率流直接相关。在碳流计算之前,需事先确定网络中的功率分布。考虑到功率分摊的准确性要求,采用精准的交流潮流模型进行分析计算。对于一个含有n个节点的电力系统,其节点有功和无功潮流平衡方程如式(1)、式(2)所示,利用牛顿-拉夫逊法进行求解,可得到各节点的电压幅值Vi和角度δi。
(1)
(2)
式中:PGi、QGi分别为接入节点i的发电机有功和无功输出;PLi、QLi分别为接入节点i的有功和无功负荷;Gij、Bij分别为支路i-j电导和电纳的负值;Ui、Uj分别为节点i和节点j的电压幅值;δij为节点i和节点j的电压角度差,即δij=δi-δj,其中δi和δj分别为节点i和节点j的电压角度。
根据上述潮流计算结果,各支路传输有功和损耗计算公式分别为
Pij=ViVj(Gijcosδij+Bijsinδij)
(3)
(4)
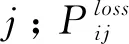
1.2 发电功率分摊
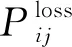
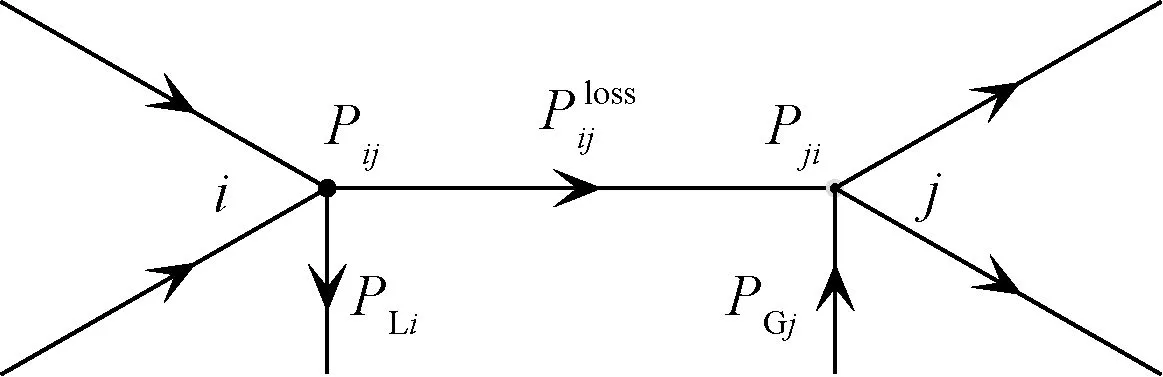
图1 支路功率与损耗Fig.1 Branch power and loss
由节点功率守恒条件,即流过节点的功率等于总流进节点功率,节点j的流过功率可表示为
(5)
式(5)中:Pj为流过节点j的功率,它等于节点j的发电注入功率PGj与各上游节点流入的功率|Pji|(支路功率Pji的绝对值)之和;Sj为节点j的上游节点集合,即与节点j直接连接,并且有功流向j的节点集合。
将式(5)改写为
(6)
式(6)中:Pi为上游节点i的流过有功功率。
进一步地,式(6)可用矩阵形式表示,即
AuP=PG
(7)
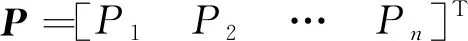
(8)
式(8)中:(Au)ji为矩阵Au中第j行第i列元素。
由式(7)可知,潮流分布矩阵Au建立了发电机功率PG与节点流过功率P之间的联系。根据节点流过功率等于总流出功率(负荷功率与流向下游节点的功率之和),可将发电功率分摊到各节点负荷、各支路功率以及网络损耗。
1.2.1 负荷从发电机汲取的功率
按比例分配原则,节点k的负荷PLk可表示为各发电机的贡献之和,即
(9)
式(9)中:ek∈Rn×1为第k个分量为1,其余分量为0的列矢量;Pk为节点k的流过功率。
节点k负荷从节点i发电机汲取的功率分量PLk,Li可表示为
(10)
式(10)中:ei∈Rn×1为第i个分量为1、其余分量为0的列矢量。
1.2.2 支路从发电机汲取的功率
假设支路k-j的功率流向为节点k到节点j,那么支路传输功率Pkj由节点k的上游发电机功率组成,按比例分配原则有
(11)
式(11)中:接入节点i的发电机对Pkj的贡献份额Pkj,Gi为
(12)
1.2.3 由发电机承担的网损功率
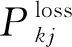
(13)
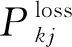
(14)
式(9)、式(11)和式(13)利用潮流分布矩阵Au成功实现了发电功率PG的分解。若给定Au和PG,则可根据式(9)、式(11)和式(13)直接得到节点负荷、支路功率以及网络损耗中各发电机提供的有功分量。考虑到发电机组的功率与其碳排放是同步产生的,两者具有一致性。若已知发电功率对应的碳排放,则可将其按有功分量进行同比例分摊,从而得到机组碳排放在电力网络中的分布特性。
2 碳排放流计算
2.1 机组碳排建模
电力系统的碳排放主要来源于化石燃料燃烧发电所产生的尾气,一般可用碳排放强度指标表示。碳排放强度为机组生产单位电能所产生的二氧化碳排放量,单位为tCO2/(MW·h)。不同类型机组的碳排放强度不同。对于水电机组、新能源机组,其生产单位电能的碳排放近似为0。对于火电机组,其碳排放强度受机组容量、燃料品质、运行状态以及负载率等因素影响,具体可用式(15)、式(16)计算。
根据机组当前运行状态和实时功率,燃煤机组的度电煤耗计算公式为
(15)
式(15)中:ai、bi、ci分别为机组i在正常运行状态下度电煤耗曲线的特性参数,可通过历史数据拟合得到;wi为机组i的度电煤耗,g/(kW·h);ζi为修正系数,其取值与机组状态有关。在正常状态下,ζi取1.0,在停机状态下ζi取0,在深度调峰和快速升降负荷时,ζi取1.01。
燃煤机组碳排放强度EGi计算公式为
(16)
式(16)中:MCO2为二氧化碳的摩尔质量,取44 g/mol;MC为碳的摩尔质量,取12 g/mol;ηi为机组i的燃煤含碳率,可通过元素分析实验获得;ξi为机组i燃煤的碳氧化率,取98%;μi为碳捕集率,取决于电厂安装的碳捕集装置的技术性能。
式(15)和式(16)为燃煤机组的碳排放强度计算公式。对于燃气和燃油机组,其碳排放强度计算公式与此类似,这里不再赘述。
2.2 碳流指标计算
式(9)、式(11)和式(13)定量给出了发电功率在节点负荷、支路功率以及网络损耗中的分布。而碳排放强度则描述了机组生产单位电能的二氧化碳排放量。因此可将机组碳排放强度与机组功率分布两者加以结合,将机组碳排放按发电功率分布进行分摊,从而得到各节点负荷、支路功率以及网络损耗所需承担的机组碳排放份额。
2.2.1 负荷碳流率
根据式(9)和式(16),可得节点k负荷的碳流率为
(17)
式(17)中:RLk为节点k负荷的碳流率,其含义为负荷每小时用电所产生的等效于发电侧的二氧化碳排放量,单位为tCO2/h;diag(PG)表示将列矢量PG转化为对角矩阵;EG为机组碳排放强度构成的矢量。
节点k负荷需承担的机组i的碳流率分量RLk,Gi为
RLk,Gi=PLk,GiEGi
(18)
2.2.2 支路碳流率
根据式(11)和式(16),可得流经支路k-j功率对应的碳流率Rkj为
(19)
接入节点i的发电机对支路k-j的碳流率贡献Rkj,Gi可表示为
Rkj,Gi=Pkj,GiEGi
(20)
2.2.3 网损碳流率
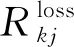
(21)
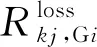
(22)
2.2.4 支路碳流密度
支路碳流密度为支路碳流率与其有功潮流的比值,它表示支路传输单位电能所造成的等效于发电侧的碳排放量,单位为tCO2/(MW·h)。对于支路k-j,其碳流密度可表示为
(23)
2.2.5 节点碳势
节点碳势为流入节点的支路碳流率之和与该节点流过功率之比,表示节点消费单位电能所产生的等效于发电侧的碳排放量,单位为tCO2/(MW·h)。对于节点j,其节点碳势可表示为
(24)
式(24)中:ENj为节点j的碳势。
2.3 碳流计算流程
所提出的电力系统碳流计算流程如图2所示,具体步骤如下。
步骤1获取当前时刻系统中各节点负荷(包括有功和无功负荷)、发电机有功和无功出力、网络拓扑结构以及电阻、电抗等相关技术参数。
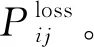
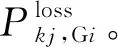
步骤4根据机组有功功率PGi和式(15)、式(16)计算各机组实时碳排放强度EGi。
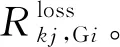
步骤6根据式(23)和式(24)计算各支路碳流密度和节点碳势等指标。
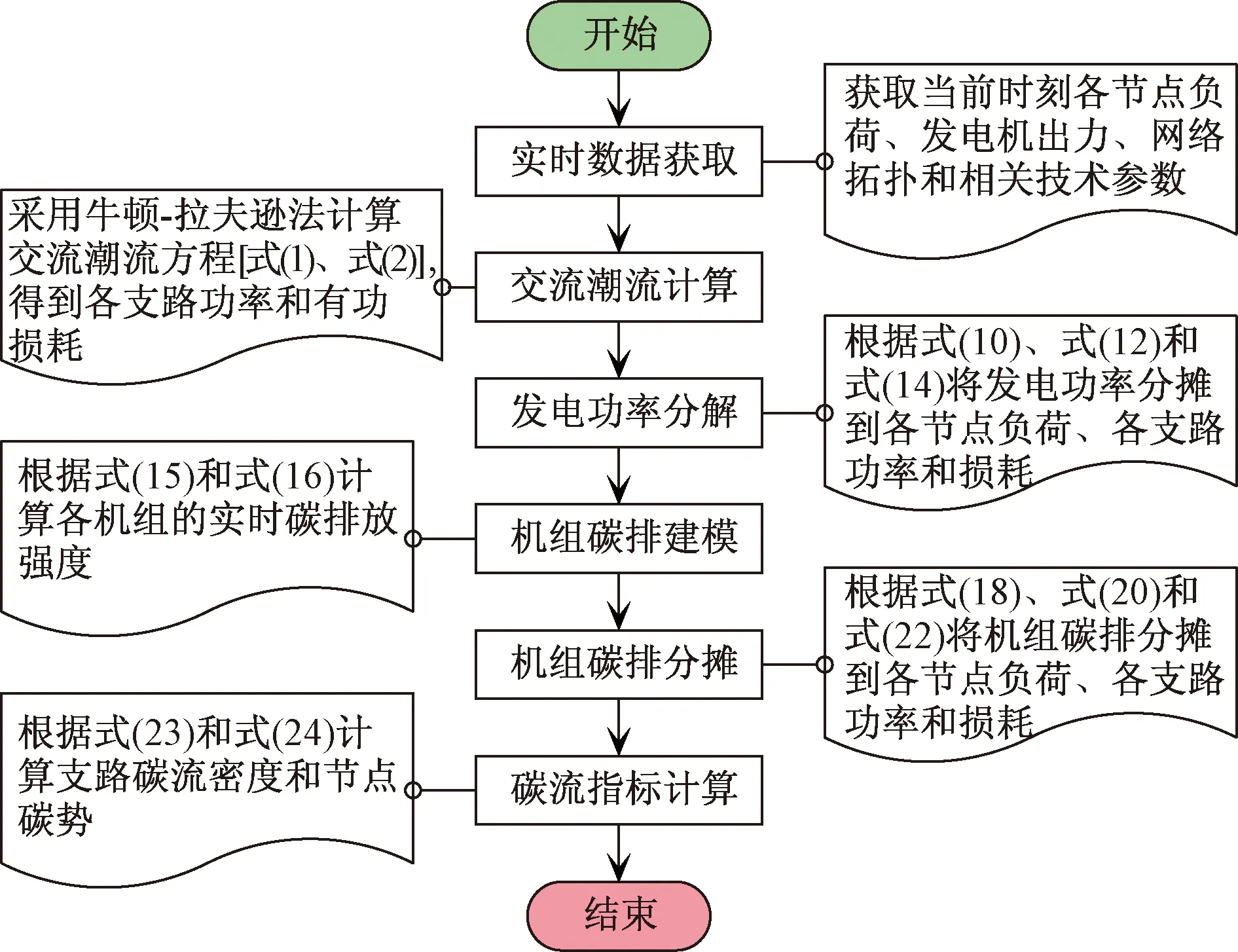
图2 碳流计算步骤Fig.2 Calculation steps of carbon emission flow
3 算例测试及分析
3.1 2机4节点系统
采用4节点系统进行测试,系统拓扑结构如图3所示。其中节点1和节点2分别接入一台火电机组,机组特性参数如表1所示;节点3和节点4为负荷节点,对应有功和无功负荷需求分别为(200+j80) MVA、(300+j120) MVA;各支路的阻抗标幺值为0.019 38+j0.059 17 p.u,对地电纳为0.052 8 p.u。采用牛顿-拉夫逊法计算该系统潮流,得到机组G1的有功出力与各支路的送端和受端有功如图3所示,送端与受端有功之差即为支路的有功损耗。
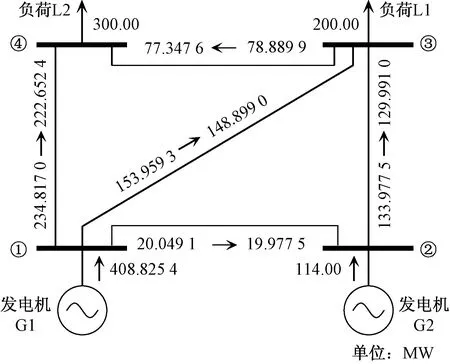
图3 4节点系统拓扑图Fig.3 Topology diagram of 4-node system

表1 机组特性参数Table 1 Unit characteristic parameters
根据潮流结果和式(5)、式(7),得到各节点发电功率为PG1=408.825 4 MW,PG2=114.0 MW,PG3=PG4=0;节点流过功率为P1=PG1=408.825 4 MW,P2=PG2+|P21|=114.0+19.977 5=133.977 5 MW,P3=|P31| +|P32|=278.889 9 MW,P4=|P41|+|P43|=300.0 MW,即有P=[408.825 4, 133.977 5,278.889 9, 300.0]T,PG=[408.825 4, 114.0, 0.0, 0.0]T。由式(8)可知,(Au)21=-|P21|/P1=-0.048 9,(Au)31=-|P31|/P1=-0.364 2,(Au)41=-|P41|/P1=-0.544 6,(Au)32=-|P32|/P2=-0.970 2,(Au)43=-|P43|/P3=-0.277 3,则潮流分布矩阵为
(25)
利用式(9)、式(11)和式(13)将发电功率分解到各节点负荷、支路功率和网络损耗,结果如表2所示。可以看出,负荷1对应的机组G1的功率分量为120.679 9 MW,机组G2分量为79.320 1 MW,两者之和正好等于其有功需求。同样,负荷2、支路功率及损耗对应的发电功率分量之和与分解前各自的功率值分别相等,结果表明本文方法能够保证分解前后的功率平衡。需要说明的是,利用文献[16]中的近似分解方法计算,可以发现支路功率与损耗的分解误差分别为0.426 4%和0.230 3%,而本文能够实现精确分解,充分显示了其优越性。进一步分析表2可知,支路1-2、1-3、1-4的有功和损耗均由机组G1承担,而支路2-3、3-4的功率和损耗则由机组G1、G2共同承担。这是由于机组G2的发电功率流向为2→3→4,而机组G1功率的流通路径包括1→4、1→3→4和1→2→3→4,因此机组G1在各条支路均有功率流动和损耗产生。
根据机组G1、G2的出力和表1中的参数,计算式(15)和式(16)可得机组G1、G2的度电煤耗分别为292.541 7和289.087 7 g/(kW·h),对应碳排放强度为0.168 2和0.831 0 tCO2/(MW·h),即EG=[0, 0, 0.168 2, 0.831 0]T。将机组排放强度EG按式(18)、式(20)和式(22)分摊,结果如表3所示。可以看出,负荷1的碳流率明显高于负荷2,结合前文可知,负荷2的有功需求大于负荷1,即两者的碳流率大小与功率大小关系相反。其原因在于高排放的机组G2给负荷1贡献了更多的CO2份额,反观机组G1虽然承担了负荷2近90%的有功需求,但是其安装的碳捕集装置使得机组G1的排放强度远低于G2,因此出现了负荷碳流率与功率“倒挂”的现象。将机组G1、G2的碳流率分量(不含支路功率碳流率)各自相加,并与其自身的注入碳流率相比,可以发现碳流率分量之和与注入碳流率相等,这说明系统满足总体碳平衡。
3.2 6机30节点系统
采用6机30节点系统进行进一步测试,系统拓扑结构如图4所示,机组G1、G2和G6为燃煤机组,碳排放强度均为0.875 tCO2/(MW·h),机组G3和G5为燃气机组,碳排放强度为0.525 tCO2/(MW·h),机组G4为水电机组,对应碳排放强度为0。
利用所提方法进行功率与碳流计算,计算后的系统功率分布与碳流分摊结果如图4所示。可以看出,机组G1的注入碳流率最大,其值为49.25 tCO2/h。燃气机组G3、G5的碳排放强度虽然小于燃煤机组,但是G3和G5的有功输出较大,导致其碳流率较燃煤机组G2和G6更大。机组G4的碳排放强度为0,即不产生二氧化碳排放,因此其注入碳流率为0,与该机组直接相连的节点和线路(节点8、线路8-6、8-28)的碳流率同样为0。

表2 机组功率分解结果Table 2 Decomposition results of unit power

表3 机组碳排分摊结果Table 3 Allocation results of unit carbon emission
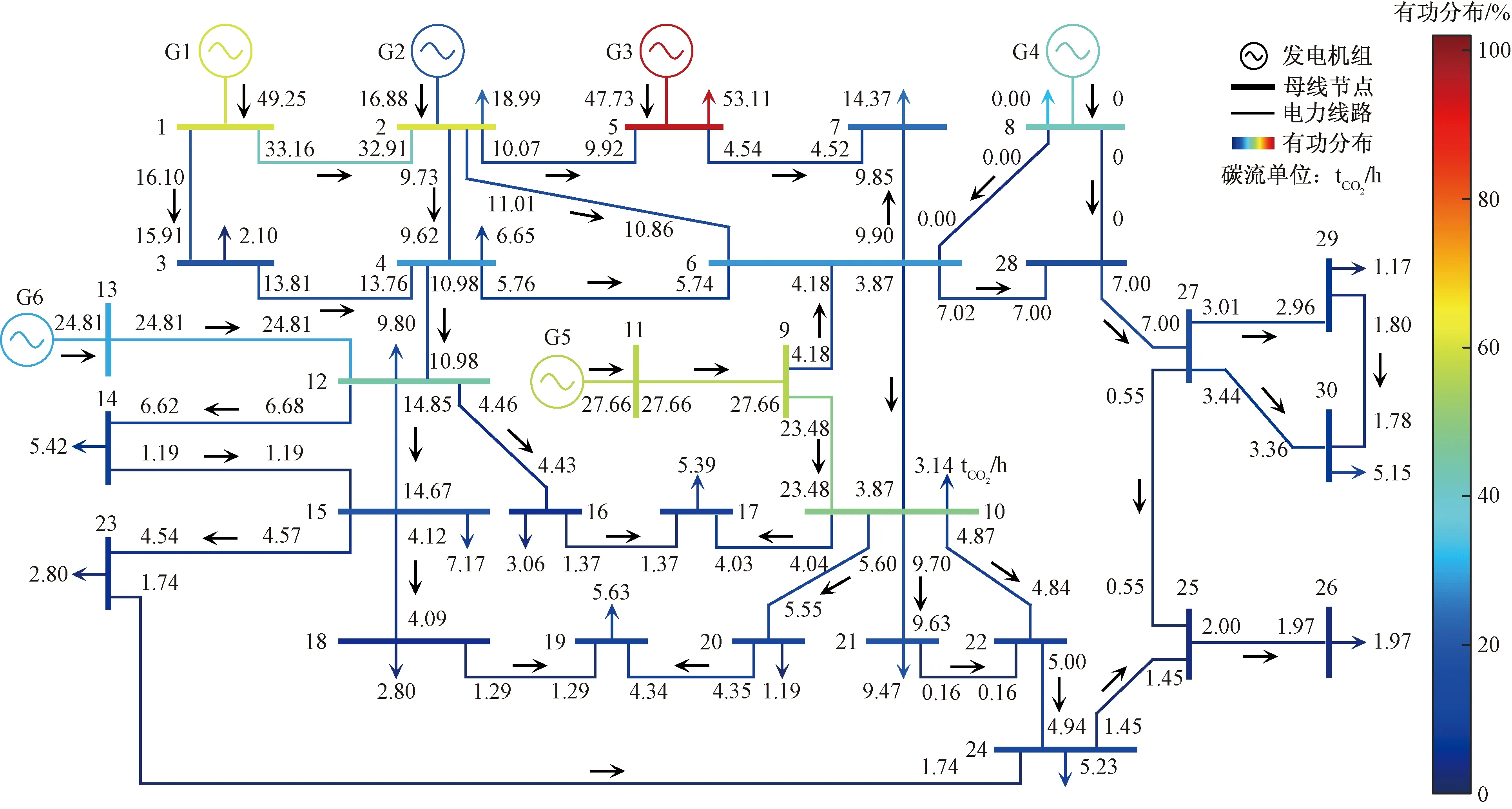
发电机、节点与线路的颜色深浅反映其有功功率的大小;箭头指示方向表示支路碳流具体流向;箭头两侧的数字表示碳流率;两侧数字之差则反映线路损耗所应承担的碳流率大小图4 30节点系统功率分布与碳流分摊结果Fig.4 Power distribution and carbon flow allocation results of 30-node system
图4中各节点的注入碳流率与流出碳流率相等。以连接最为复杂的节点10为例,节点6和节点9分别通过线路6-10、9-10向节点10贡献了总计27.35 tCO2/h的碳流率,而从节点10流向节点17、20、21、22以及节点10负荷的碳流率之和为27.35 tCO2/h,可见节点满足碳流平衡关系,即流入节点的碳流等于流出节点的碳流。如前所述,箭头两侧碳流率之差即为支路损耗应承担的碳流率。如线路1-2的有功损耗0.29 MW,对应损耗碳流率为0.25 tCO2/h,而支路4-12、9-10、28-27因电阻为0导致其损耗碳流率均为0。该结果说明减少线路损耗有助于降低系统碳排放。
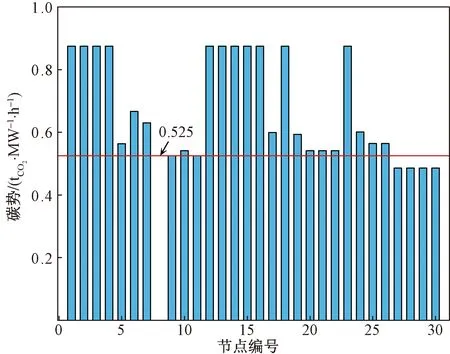
图5 各节点的碳势分布Fig.5 Carbon potential distribution of each node
各节点碳势分布如图5所示。可以看出,节点1、2、13的碳势等于接入各节点机组的碳排放强度,即0.875 tCO2/(MW·h)。结合图4分析可知,节点3、4的注入碳流全部来源于节点1,因此其碳势与节点1碳势相等。同理,节点12、14、15、16、18、23的碳流均由节点1、2、13提供,故上述节点的碳势均一致。节点5的碳势大于接入该节点的机组碳排放强度,这是因为排放强度高的燃煤机组G2通过线路2-5为其注入了一部分碳流,从而抬升了该节点的碳势。节点27~30的碳势均低于燃气机组的碳排放强度,其原因在于零排放的水电机组G4稀释了注入节点27~30的碳流,从而拉低了上述节点的碳势。以上结果表明,节点碳势与节点附近的机组碳排放强度相关。当发现某区域整体碳势较高时,可对区域内的机组进行改造,以达到降低该区域总体碳排放的效果。
4 结论
为了实现电力系统碳排放流的精准计算与分摊,提出了一种基于潮流分布矩阵的电力系统碳流计算方法。该方法首先以交流潮流为基础,通过建立机组功率到节点功率的映射,实现发电功率的准确分解;然后构造多因素影响的机组碳排放模型,并借助碳流与功率流同分布的特征,将发电侧碳排放公平分摊到节点负荷、支路功率和网络损耗,成功揭示了碳排放在电力网络中的传输和流动过程。4节点和30节点系统的测试结果表明,本文提出的碳排放流计算方法,可以精准计算电力系统的实时碳流分布,合理划分不同主体的碳排放责任,对于制定碳减排措施、辅助碳审计决策、助力电力低碳发展具有良好的实用价值。
