连续被动式运动训练器转速切换协调控制方法

胥 燕，郑忠文

（1.成都医学院，四川 成都 610500；2.阜阳师范大学，安徽 阜阳 236000）

1 引言

连续被动式运动训练器主要用于手术后肩关节、膝关节、踝关节、骨关节等可动域功能的恢复，是在连续被动运动原理基础上制成的装置［1-2］。但目前连续式被动式运动训练器由于动力装置的原因，存在可靠性差、结构复杂和噪声大的特点，为此，需要对训练器转速切换协调控制方法进行研究。

文献［3］提出基于预测模型的训练器转速切换控制方法，该方法在动力学模型的基础上建立控制增量形式的预测模型，建立满足约束条件的预测控制模型，实现运动器转速切换的控制。文献［4］提出基于模糊补偿的训练器转速切换控制方法，该方法采用人机协作映射关系结合模糊补偿算法实现训练器转速切换控制。但上述方法没有提取表面肌电信号的特征，控制所用的时间较长，存在控制效率低的问题。

为了解决上述方法中存在的问题，提出连续被动式运动训练器转速切换协调控制方法。通过时域分析法将信号转换为特征值，建立连续被动式运动训练器的运动学模型，来抑制训练器扭振，并通过引入角速度和位置作为状态变量，改善转速控制的抗干扰能力；设计转速切换协调控制器，从而提高转速控制的精度，完成训练器转速切换协调控制方法的设计。通过仿真实验验证，该方法具有较良好的转速切换协调控制性能。

2 表面机电信号特征提取

连续被动式运动训练器转速切换协调控制方法通过时域分析法将信号转变为时间变量函数，通过滤波和整形处理获得Wil⁃lison幅值、积分机电值、幅值直方图、平均肌电值、过零次数、均方根六个特征值［5-6］。

设WAMP代表的是Willison值，其计算公式如下：

式中：N—采样点数量；xi—肌电信号样本值。

设AV代表的是平均肌电值，其计算公式如下：

肌电信号在不同活动程度肌肉下与基线偏离的程度都不相同，将不同幅值段中存在的SEMG 信号的采样个数作为有效特征。在提取特征值之前需要选取一个阈值，对正负阈值间存在的距离进行划分，获得大小不同的幅值段，将不同幅值段中存在的SEMG采样点个数作为肌电信号的特征值［7-8］。

设IAV代表的是绝对值积分平均值，可通过下式计算得到：

设ZC代表的是过零点数，连接数据点，并对正负穿越零点的次数进行计算：

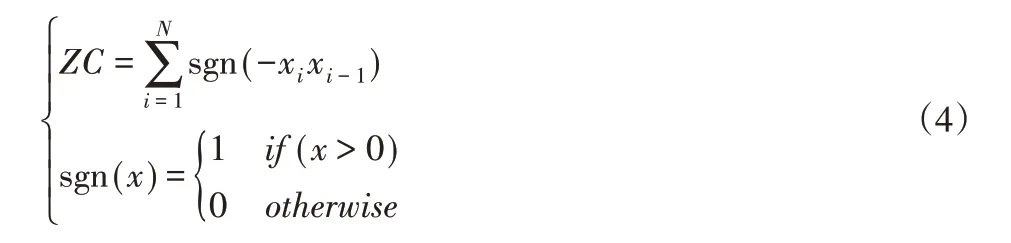
设VAR代表的是方差，RMS代表的是均方根，std代表的是标准差，其表达式如下：

式中：xLAV—肌电信号对应的绝对积分平均值；

3 训练器转速切换协调控制方法

3.1 训练器模型

连续被动式运动训练器模型，如图1所示。

图1 连续被动式运动训练器模型Fig.1 Model of Continuous Passive Exercise Trainer

通过下式描述连续被动式运动训练器的运动学模型：

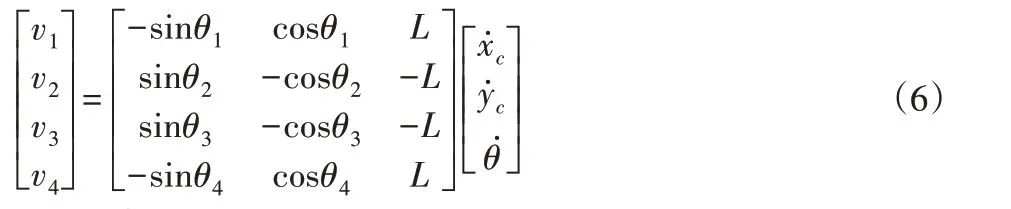
可用下述公式描述上式：

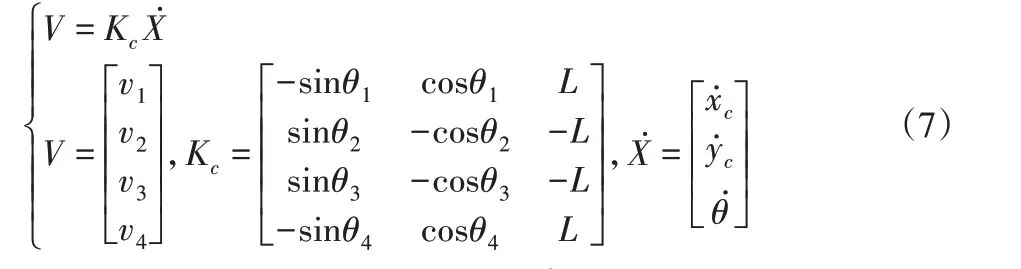
在上述方程的基础上获得速度约束方程v1+v2=v3+v4。

通过下述公式描述连续被动式运动训练器的运动模型：

通过下述公式描述连续被动式运动训练器的动力学模型：

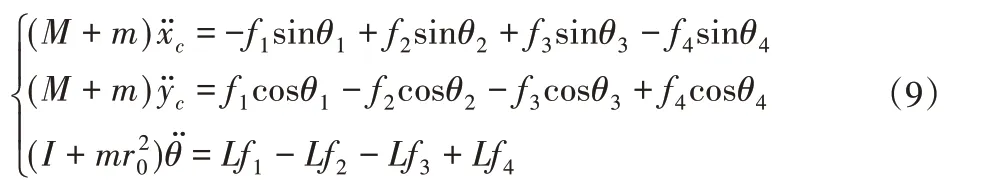
M—连续被动式运动训练器的质量；

f1、f2、f3、f4—系统的输入；

m—康复者对应的等效质量；

L—全方向轮与中心之间存在的距离；

I—训练器对应的转动惯量；

r0—训练器的中心与重心之间存在的距离。

3.2 速度解耦模型

将V′=rw带入连续被动式运动训练器的动力学模型中，获得下式：

式中：w=[w1w2w3]T；r—轮子半径。

假设在连续被动式运动训练器中存在4个输入力，其中存在一个冗余的力，连续被动式运动训练器在跟踪过程中只需要3个力就可以完成转速切换的协调控制［9-10］，令f2=f4，获得整理后的连续被动式运动训练器的动力学模型，其中：

在数学模型的基础上构建连续被动式运动训练器系统的状态方程：

选取连续被动式训练器的角速度w和位置X作为状态变量，获得放射非线性系统方程：

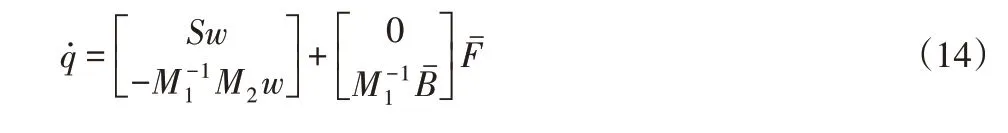
用下述方程描述连续被动式运动训练器系统的数学模型：

式中：u—动力学模型的新输入控制量，可将连续被动式运动训练器系统的输出定义为获得完整的连续被动式运动训练器的仿射非线性系统模型：

3.3 控制器设计

通过设计反馈控制器实现连续被动式运动器训练转速切换的协调控制，根据控制与角速度之间存在的线性关系，设计转速切换协调控制器：

式中，ei—误差；Kpi—常数—参考角速度。

4 实验与分析

为了验证连续被动式运动训练器转速切换协调控制方法的整体有效性，需要对连续被动式运动训练器转速切换协调控制方法进行测试，本次测试在MATLAB软件中进行，操作系统为Win⁃dows10，CPU 处理器为2.80GHz X64。其中，选取的连续被动式运动训练器的结构，如图2所示。

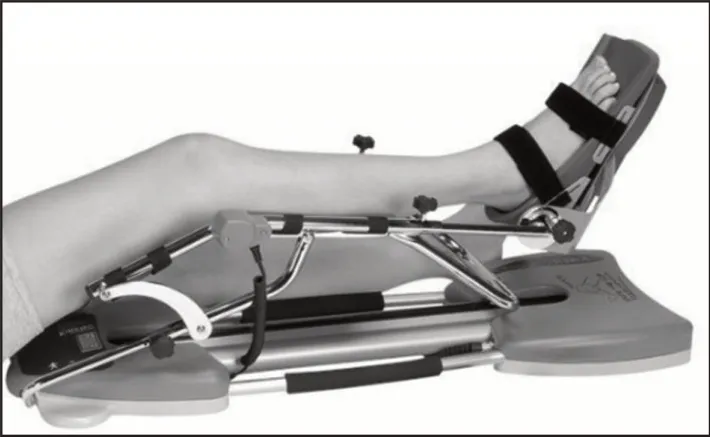
图2 连续被动式运动训练器结构示意图Fig.2 Structure Diagram of Continuous Passive Sports Trainer

将转速控制误差作为测试指标，采用连续被动式运动训练器转速切换协调控制方法（方法1）、基于预测模型的训练器转速切换控制方法（方法2）和基于模糊补偿的训练器转速切换控制方法（方法3）进行对比实验，连续被动式运动训练器系统控制的转速对比结果，如图3所示。

图3 连续被动式运动训练器系统控制的转速对比结果Fig.3 Speed Comparison Results of Continuous Passive Sports Trainer System Control

统计三种方法下多次迭代的平均转速控制误差，测试结果，如图4所示。

图4 控制误差测试结果Fig.4 Control Error Test Results

分析图4 中的数据可知，采用方法1 对运动训练器转速进行协调控制时在多次迭代中的控制误差均控制在0.2rad/s以下，采用方法2和方法3对运动训练器转速进行协调控制时，获得的控制误差分别在第1 次迭代和第2 次迭代中高达0.6rad/s 和0.7rad/s，方法1进行协调控制的误差较低，因为方法1获取了表面肌电信号，并提取了表面肌电信号的特征，降低了方法1的控制误差。

设置稳定性系数φ，在区间［0，1］内取值，稳定性系数越高，表明控制方法的控制稳定性越好，测试结果，如图5所示。

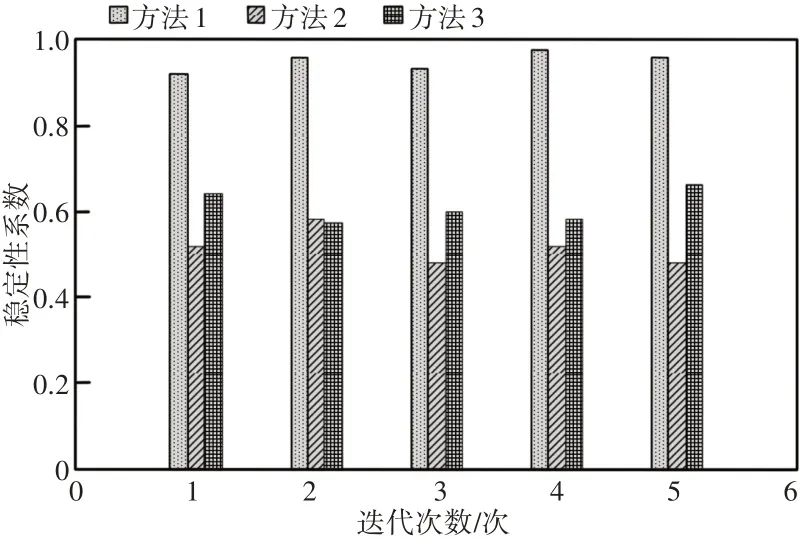
图5 稳定性系数测试结果Fig.5 Test Results of Stability Coefficient

对图5中的数据进行分析可知，采用方法1对运动训练器的转速切换进行控制时，在多次实验过程中获得的稳定性系数均在0.9以上，方法2和方法3对运动训练器的转速切换进行控制时，在多次实验过程中获得的稳定性系数分别在0.5和0.6附近波动，方法1的稳定性系数远远高于方法2和方法3的稳定性系数，因为方法1根据获取的表面肌电信号特征构建了连续被动式运动训练器系统的动力学模型，提高了控制稳定性。

将控制效率作为测试指标，采用方法1、方法2和方法3进行测试，通过控制时间对比不同方法对运动训练器转速切换控制的效率，测试结果，如图6所示。

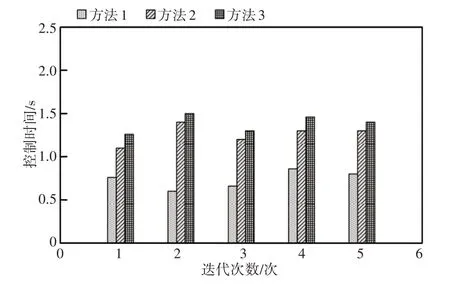
图6 控制效率测试结果Fig.6 Control Efficiency Test Results

通过图6可知，在多次控制实验过程中，方法1将控制时间保持在1.0s之内，方法2和方法3的控制时间均高于1.0s。方法1控制运动训练器转速切换所用的时间较少，因为方法1获取了表面肌电信号，根据表面肌电信号的特征在较短的时间内建立转速切换协调控制器，提高了方法1的控制效率。

5 结束语

这里提出连续被动式运动训练器转速切换协调控制方法，获取表面肌电信号，并提取信号特征，根据提取的特征构建转速切换控制器，实现连续被动式运动训练器转速切换。通过仿真实验证明，设计方法的转速控制误差保持在0.02rad/s之内，稳定性系数在0.9以上，控制时间保持在1s之内，整体转速切换协调控制性能较好。