半导体颗粒整列的整列板运动振型分析
2022-05-19李延民刘锡山庄天宇
李延民,王 振,刘锡山,庄天宇
(郑州大学机械工程学院,河南 郑州 450001)
1 引言
整列机是一种使颗粒物料按照固定的间距和方向自动整齐排列的装置。整列机主要由整列板来完成颗粒物料的整列,整列板上表面分布有固定间距的凹槽。整列机的振动装置驱动整列板振动,板上散乱分布的颗粒与整列板之间发生相对运动并落入凹槽中,从而实现自动整齐排列。目前,文献[1-2]发明了使整列板进行二自由度运动的整列机,相对于人工实现颗粒物料的整列,整列机的使用加快了整列速度,但现有整列机的整列板运动自由度少,颗粒在整列过程中难以快速分散,限制了整列速度的提升。为了解决这一问题,文献[3-9]对物料在多自由度振动筛板上的透筛进行仿真分析,结果表明振动板的多自由度运动有利于物料的快速散开和均布。
为了找出适合制冷片中半导体颗粒整列的最佳运动振型,实现半导体颗粒的快速自动化整列,利用ADAMS软件建立半导体颗粒在整列板上的运动仿真模型。运用正交试验法设计仿真方案来分析不同因素对半导体颗粒整列速度的影响,以半导体颗粒完成整列所需最短时间为仿真指标,对半导体颗粒在整列板上的整列进行动力学仿真。通过对仿真数据的对比分析,找出整列板的最佳运动振型,为新型整列机的结构设计和参数选择提供参考依据。
2 仿真模型的建立
2.1 制冷片的基本结构
制冷片由陶瓷板、导流片、半导体颗粒组成的新型制冷设备。半导体颗粒分为P型半导体和N型半导体,它们之间按固定的间距交错排列,导流条是一种镀锡铜片,把交错排列的P型半导体和N型半导体连接成完整的线路,陶瓷板是一种绝缘但导热性好的氧化铝板,半导体颗粒和导流片组成的完整线路焊接在陶瓷板上,构成制冷片的主体结构。以TECL-12703型制冷片为例,该制冷片中有127对尺寸为(1.1×1.1×2.1)mm的P型和N型半导体,陶瓷板面积为(40×40)mm。该制冷片的内部结构,如图1所示。

图1 制冷片的基本结构Fig.1 The Basic Structure of Cooling Sheet
2.2 整列板结构设计
整列板主要是由模具板、回收板、挡板构成,根据陶瓷板和半导体颗粒的大小确定模具尺寸为(40×40×10)mm,凹槽为(1.5×1.5×2.1)mm。凹槽位置由半导体颗粒在陶瓷板上的分布位置确定。整列板包含12块模具板,回收板分布在模具板前后两端,挡板分布在模具板的左右两侧。在整列过程中回收板和挡板可以阻挡半导体颗粒飞出整列板;整列结束后,回收板可以收集多余的半导体颗粒。
在建立仿真模型时,先利用SolidWorks软件建立整列板三维简化模型,导入到ADAMS软件中。在整列板上的不同位置添加10颗半导体颗粒模型,以整列板的纵向为X轴方向,整列板横向为Y轴方向,整列板的法向为Z轴方向,建立的仿真运动模型,如图2所示。

图2 仿真运动模型Fig.2 Simulated Motion Model
根据半导体颗粒与整列板的相关材料特性,在对半导体颗粒在整列板上的运动进行动力学仿真前,对颗粒与颗粒、颗粒与整列板之间添加相关的参数设置,如表1所示。

表1 接触参数设置Tab.1 Contact Parameter Setting
3 半导体颗粒的受力分析
为了实现半导体在整列板上的分布均匀,在整列时对整列板添加沿Y轴方向的摆动。对摆角为α的整列板上的半导体颗粒进行受力分析,半导体颗粒在整列板上主要受重力G、支撑力N、摩擦力F和惯性力μ,受力情况,如图3、图4所示。其中:

图3 颗粒沿整列板后滑趋势Fig.3 The Back Tendency of Particles to Slide Along the Entire Panel

图4 颗粒沿整列板前滑趋势Fig.4 The Front Tendency of Particles to Slide Along the Entire Panel

式中:m—半导体颗粒的质量;a—整列板的运动加速度;φ—半导体颗粒与整列板之间的摩擦角。
颗粒沿整列板向后发生相对运动的极限条件是:

将上述μx和Fx带入式中可得:

颗粒沿整列板向前发生相对运动的极限条件是:

同理得:
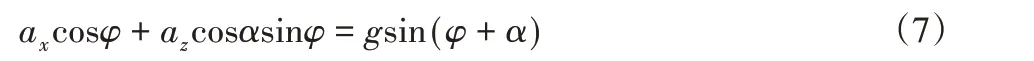
颗粒沿整列板横向发生相对运动的极限条件是:

将上述μy和Fy带入式中可得:

颗粒沿整列板法向不脱离整列板的极限条件为N≥0。

通过上述计算可知,半导体颗粒在整列板上的运动状态主要与整列板的运动加速度、整列板的摆角有关。整列板在振动时主要做简谐运动,简谐运动的加速度与运动振幅和角速度有关,所以整列板上半导体颗粒的运动状态不仅取决于整列板的运动自由度,还与整列板运动过程中的运动振幅、角速度和整列板的摆角有关。要实现在整列板运动过程中半导体颗粒能进入整列板的凹槽中,颗粒与整列板之间就需要有相对运动。在对整列板的运动参数进行选择时,必须满足半导体颗粒在不脱离整列板的基础上实现相对运动的条件。
4 仿真分析设计方案
为了研究整列板的不同运动振型对板上半导体颗粒的运动状态的影响,找出适合半导体颗粒整列的最佳运动振型及运动参数,使半导体颗粒能够快速高效的完成自动整齐排列,在建立的整列板仿真模型的基础上,在ADAMS软件中对整列板分别添加不同运动振型的位移驱动方程[10],对半导体颗粒在整列板的运动状态进行动力学仿真。
通过分析传统的三种振动筛:直线振动筛、圆振动筛和旋振筛中振动筛板的运动振型基础上,考虑在半导体颗粒整列完成后多余颗粒的方便回收,对整列板仿真模型添加以下三种多自由度运动振型:
(1)沿Y轴、Z轴的简谐运动和绕Y轴的摆动;
(2)沿垂直面的圆周运动和沿Y轴的简谐运动以及绕Y轴的摆动;
(3)沿水平面的圆周运动和沿Z轴的简谐运动以及绕Y轴的摆动。
在ADAMS 软件中对整列板的仿真模型分别添加上述三种运动振型的位移驱动方程[10],设置仿真时间和仿真步数,在整列板位移驱动方程中包含有影响半导体运动状态的运动参数,在每个影响因素中选取相关的参数水平,运用正交试验方法设计仿真方案来分析不同影响因素对半导体颗粒整列速度的影响,运行动力学仿真,仿真指标为半导体颗粒在整列板上完成整列花费的时间t。
通过对比整列板在不同运动振型下半导体颗粒的整列速度,找出适合半导体颗粒整列的最佳运动振型及运动参数,为适合颗粒自动化整列的整列机的研发提供理论参考依据。
5 仿真过程和结果分析
5.1 沿Y、Z轴的简谐运动和绕Y轴的摆动
为了使整列板沿Y轴和Z轴方向的简谐运动及绕Y轴方向摆动,在ADAMS软件中添加整列板的驱动为沿Y轴和Z轴方向的运动位移方程Sy、Sz及绕Z轴方向摆动角度θ如下:

式中:Ay、Az、ωy、ωz—整列板沿Y轴和Z轴方向的振幅和角速度;θd、ωd—整列板绕Y轴摆动的最大摆角和角速度。
影响整列板上半导体颗粒运动的因素为整列板的运动参数Ay、Az、ωy、ωz、θd、ωd,对以上6个因素各取5水平,如表2所示。
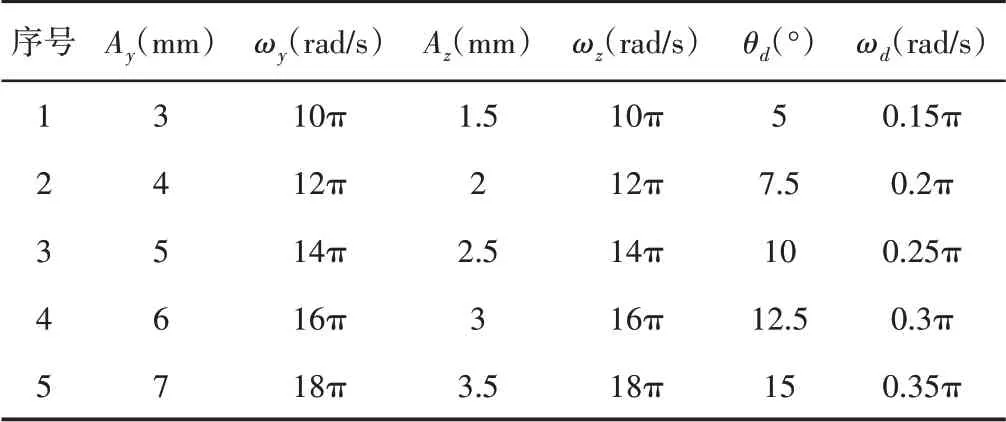
表2 因素水平表Tab.2 Factor Level Table
查正交试验表[11]得6 因素5 水平的正交试验次数为25 组。在整列板位移方程中输入相关参数并运行仿真,得到各组仿真中半导体颗粒完成整列花费时间t。根据仿真结果计算出各因素水平下的平均整列时间,如图5所示。针对缩短整列时间,由图5可知,该运动振型的各试验因素最佳组合为Ay3ωy2Az2ωz4θd3ωd2。把该参数组合输入整列板的位移方程中,再次运行仿真,得出颗粒完成整列的时间为1.46s。
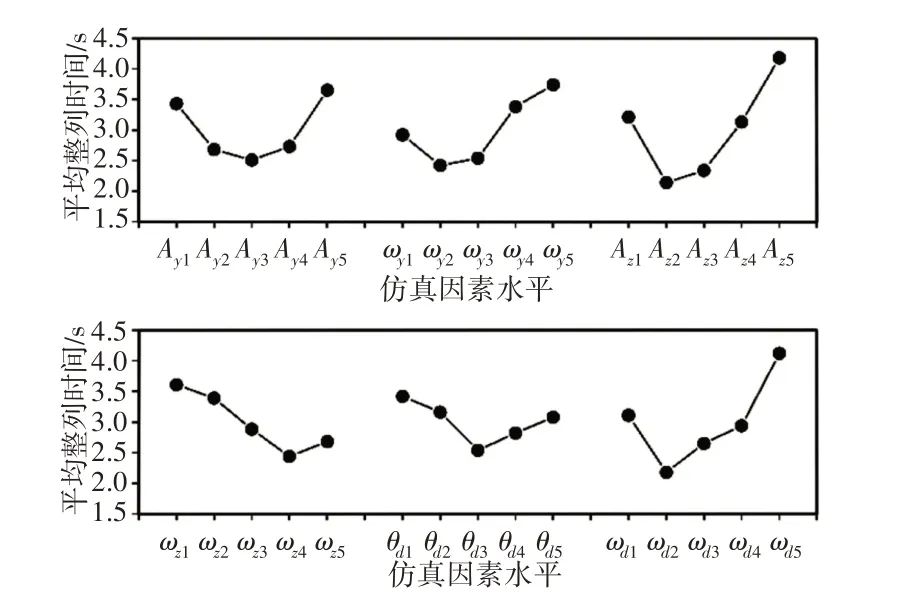
图5 仿真因素对颗粒整列速度的影响Fig.5 Influence of Simulation Factors on the Speed of Particle Array
5.2 沿垂直面的圆周运动和沿Y轴的简谐运动以及绕Y轴的摆动
为了使整列板沿垂直方向的圆周运动、沿Y轴的简谐运动和绕Y轴的摆动,对整列板添加驱动为沿X轴、Y轴和Z轴方向的运动位移方程Sx、Sy、Sz及绕Y轴方向摆动角度θ如下:

式中:R、ω—圆周运动的半径和角速度;
δ—整列板与振动方向的夹角;
Ay、ωy—Y轴方向的振幅和角速度;
θd、ωd—绕Y轴摆动最大摆角和角速度。
影响整列板上半导体颗粒与整列板之间发生相对运动的因素为整列板运动参数R、ω、Ay、ωy、θd、ωd,对以上6个因素各取5水平,如表3所示。
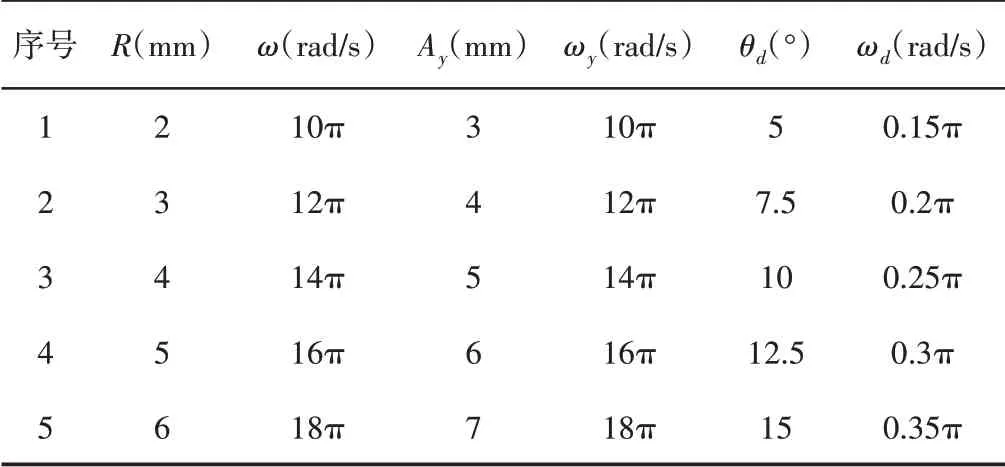
表3 因素水平表Tab.3 Factor Level Table
在整列板位移方程中输入相关参数并运行仿真,得到各组仿真中半导体颗粒完成整列花费时间t。
根据仿真结果计算出各因素水平下的平均整列时间,如图6 所示。针对缩短整列时间,由图6 可以看出,该运动振型的各试验因素最佳组合为R2ω2Ay3ωy1θd3ωd2。把最佳参数组合输入整列板的位移方程中,再次运行仿真,得出颗粒完成整列的时间为1.25s。

图6 仿真因素对颗粒整列速度的影响Fig.6 Influence of Simulation Factors on the Speed of Particle Array
5.3 沿水平面的圆周运动和沿Z轴的简谐运动以及绕Y轴的摆动
为了使整列板沿水平方向的圆形运动、Z轴的简谐运动和绕Y轴的摆动,在ADAMS软件中添加整列板的驱动为沿X轴、Y轴和Z轴方向的运动位移方程Sx、Sy、Sz以及绕Y轴方向摆动角度θ如下:

式中:R、ω—圆周运动的半径和角速度;
δ—整列板与振动方向的夹角;
Az、ωz—Z轴方向的振幅和角速度;
θd、ωd—绕Y轴摆动最大摆角和角速度。
影响整列板上半导体颗粒与整列板之间发生相对运动的因素为整列板的运动参数R、ω、Az、ωz、θd、ωd,根据正交试验方法对以上6个因素各取5水平,如表4所示。
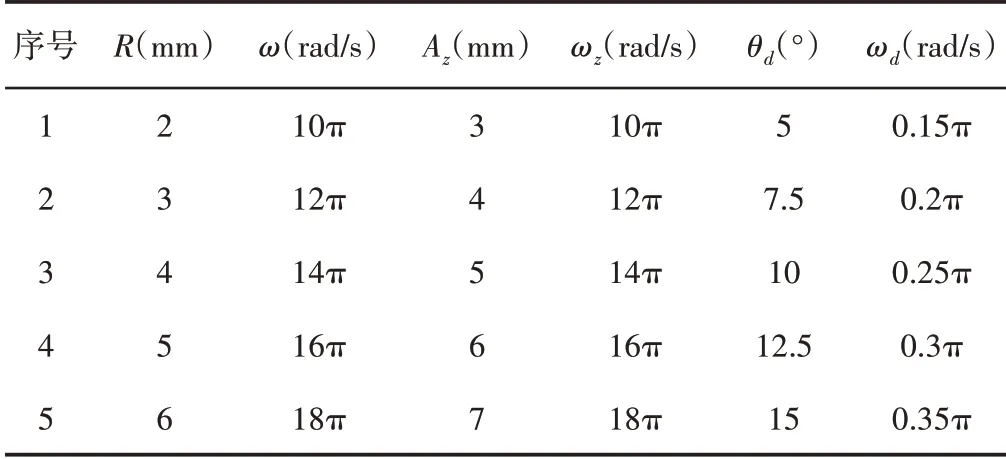
表4 因素水平表Tab.4 Factor Level Table
在整列板位移方程中输入相关参数并运行仿真,得到各组仿真中半导体颗粒完成整列花费时间t。
根据仿真结果计算出各因素水平下的平均整列时间,如图7所示,针对缩短整列时间,由图7可知,该运动振型的各试验因素最佳组合为R3ω2Az2ωz4θd3ωd2。把最佳参数组合输入整列板的位移方程中,得出颗粒完成整列的时间为1.02s。通过对三组仿真数据的对比,得出半导体颗粒整列的最佳运动振型为沿水平方向的圆周运动和沿Z轴的简谐运动以及绕Y轴的摆动,该运动振型最佳运动参数组合为R=4mm、ω=12πrad/s、Az=3mm、ωz=14πrad/s、θd=10°、ωd=0.2πrad/s。
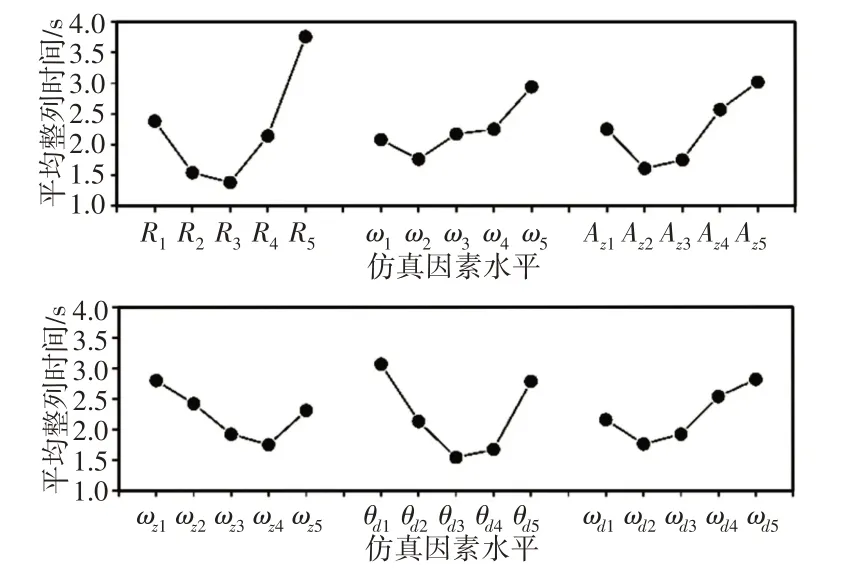
图7 仿真因素对颗粒整列速度的影响Fig.7 Influence of Simulation Factors on the Speed of Particle Array
6 结论
(1)针对制冷片中半导体颗粒实现自动化整齐排列的问题,根据颗粒的排列间距和方向设计上表面布满凹槽的整列板,利用半导体颗粒在整列板上发生相对运动并落入凹槽中,实现半导体颗粒的自动化整列。
(2)利用ADAMS虚拟仿真软件建立半导体颗粒在不同运动振型的整列板上的运动学仿真模型。
(3)对半导体颗粒在多自由度运动的整列板上的受力情况进行分析,找出整列板上半导体颗粒运动状态的影响因素。
(4)对半导体颗粒在整列板上的运动进行动力学仿真时,运用正交试验方法设计仿真方案来分析不同影响因素对半导体颗粒整列速度的影响,找出各影响因素的最优运动参数水平。
(5)对整列板在上述三种运动振型下半导体颗粒的整列速度进行分析,整列板在沿水平方向的圆周运动和Z轴的简谐运动以及绕Y轴的摆动时,各运动参数为R=4mm,ω=12πrad/s,Az=3mm,ωz=14πrad/s,θd=10°,ωd=0.2πrad/s时,10颗半导体颗粒完成整列的速度最快。
(6)通过对半导体颗粒在上述三种振型的整列板上进行动力学分析,找出适合半导体颗粒整列的最佳运动振型及各影响因素的最优参数取值,为新型整列机的结构设计和参数选择提供参考依据。
