有界广义GMM和无阈值递归图的特征提取方法及应用

赵心阳，肖 涵，2，吕 勇，2

（1.武汉科技大学机械自动化学院，湖北 武汉 430081；2.武汉科技大学冶金装备及其控制教育部重点实验室，湖北 武汉 430081）

1 引言

齿轮传动广泛应用于机械设备中，但由于工况的复杂多变，齿轮自身也容易发生故障，统计表明，在齿轮箱的全部零件中，齿轮自身失效引起的设备故障约占全部故障的60%［1］，因此针对齿轮故障诊断方法的研究一直是近年来的热点。齿轮振动信号更多的表现出非线性、非平稳特征是普遍共识［2］，学者往往将振动信号的非线性特征，如Lyapunov指数、分形维数、熵等用于故障诊断，取得一定的效果［2-3］。但由于振动信号通常信噪比较低，而上述参数对噪声较敏感，导致其作为特征量时，故障识别精度不高。

递归性是动力学系统的基本属性之一，1987年Eckman基于相空间重构理论提出递归图（Recurrence Plot，RP）分析方法［4］，用以从递归图的内部层状结构揭示时间序列的复杂性和可预测性，包括传统阈值递归图（Thresholded Recurrence Plot，RP）和无阈值递归图（Un-Thresholded Recurrence Plot，URP）。为了解决递归图分析方法无法定量描述动力学特性等问题，文献［5-6］提出传统阈值递归图特征提取方法-递归定量分析（Recurrence Quantifica⁃tion Analysis，RQA）。通过研究递归点的分布规律，研究者已提出的递归参量已达20余种，且已应用于设备故障诊断领域。但递归参量的选择往往由研究者主观确定，且故障识别精度有待提高。由于URP中递归点间的距离参数被保留下来，因此对于同一时间序列，URP 中往往包含比RP 更多的信息量，近年来针对URP 的研究逐渐成为热点。2018年，文献［7］提出利用URP 分析方法检测绝缘电力电缆因热老化引起的劣化程度。文献［8］根据URP中的欧式距离分布提出了一种基于无阈值递归矩阵的检测器，用于检测噪声环境中信号的出现。但上述研究均是从定性角度分析，无法定量描述URP，限制了其应用。这里提出一种采用有界广义高斯混合模型（BGGMM）进行URP特征提取的方法，用于URP的定量分析，并应用于齿轮故障分类。

2 算法

2.1 无阈值递归图

递归图作为时间序列中重复模式的图形表示，是分析时间序列周期性、混沌性以及非平稳性的一个重要方法［2］。算法流程如下：

（1）对于一维时间序列xi(i=1，2，3，…N)，经相空间重构后，得到高维相空间：

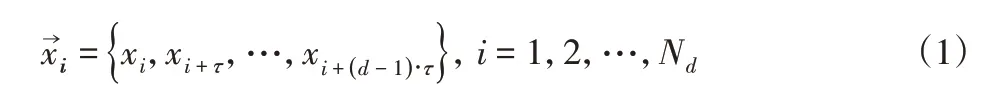
式中：Nd=N-(d-1)τ，τ—延迟时间；d—嵌入维数。

（2）对于相空间中的轨迹x→i(i=1，2，…Nd，x∈Rd)，无阈值递归图定义为：

式中：‖ ∙‖—向量范数，常用范数包括1-范数，2-范数和∞-范数，这里采用∞-范数；与传统阈值递归图不同，无阈值递归图由于没有阈值ε的限定，其递归矩阵Ri，j(unthres)—相空间中两个向量x→i和x→j之间的欧式距离。

2.2 有界广义高斯混合模型

基于高斯分布的混合模型一直都是研究的热点，广泛应用于模式识别、图像处理和故障诊断等领域。其中高斯混合模型（GMM）［9］是应用较多的混合模型之一，但由于其具有奇异性，即样本数不足时参数估计会更加困难，从而导致算法发散。为解决GMM 的不足，学者提出更具鲁棒性的广义高斯混合模型（GGMM）［10］。相较于传统GMM，GGMM 嵌入额外参数λ用以控制拟合曲线尾部凸起与否，因此可适应更多类型数据。但是上述混合模型都未考虑数据边界问题，当数据存在支撑边界时，将导致参数估计存在较大的偏差。因此文献［11］2014年提出有界广义高斯混合模型（BGGMM）用以拟合高斯分布和非高斯分布数据，并考虑数据的边界问题，近年来广泛用于模式识别等领域。文献［12-13］成功将BGGMM 应用于视频和图像降噪以及图像分割领域。文献［14］结合独立分量分析方法（ICA）和BGGMM成功实现对关键字进行无监督识别。

2.2.1 算法简介

高斯混合模型（GMM）是单高斯概率密度函数的延伸，广泛应用于模式识别、图像处理、故障诊断［6］等领域。

K个分量的GMM，其定义为：

式中：Θj—模型参数，ωj作为混合权重系数，满足ωj≥0。

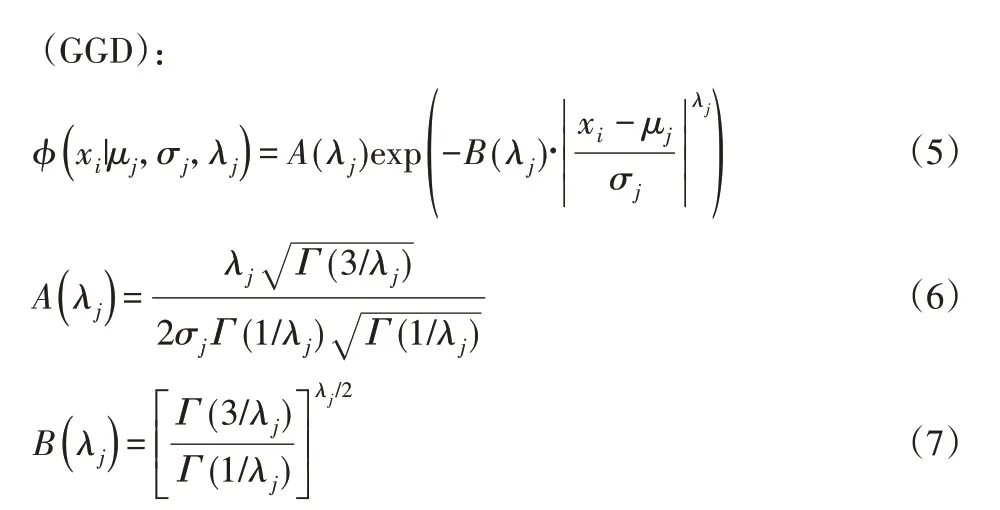
式中：μj和σj—混合模型中的均值和方差，参数λj控制该分布的尾部凸起与否；Γ(∙)—伽马函数。值得提出的是，GMM 和GGMM是BGGMM的特殊情况：当λj=2，H(xi|Ωj)=1时，式（4）可表示为GMM的概率密度函数；当H(xi|Ωj)=1时，表示为GGMM的概率密度函数。

2.2.2 参数估计

期望最大化（Expectation-Maximum，EM）算法在统计学中广泛被用于参数的最大似然估计，同时也是基于高斯分布的混合模型中常用的参数估计方法［15］。EM算法以迭代的形式实现最大似然函数的最大化，包括E-Step 和M-Step，在这里所应用的BGGMM中，最大似然函数定义如下：

为了最大化式（8），采用其负数方程作为误差方程，此时最大化似然函数即等效为最小化误差式（9），误差方程定义如下：

在E-Step中，后验概率定义为：

在M-Step 中，根据式（10）得出的后验概率更新模型参数如下：

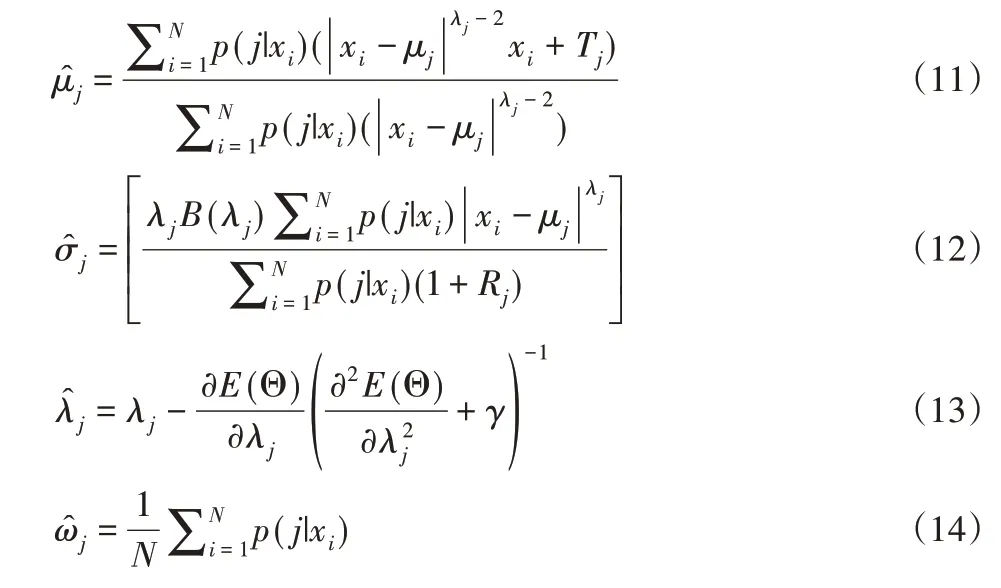
其中：

式中：γ—比例因子—从混合模型特定组分j的广义高斯分布中提取的随机变量；M—大正整数；当x≥0时，sign(x)=1，否则sign(x)=0。

最后，对式（9）中的误差函数进行评估，检查收敛准则。若不满足收敛条件，则从E-Step重新开始下一次迭代，直到满足收敛准则为止。

3 URP统计定量分析

无阈值递归图（URP）可以检测递归点之间距离的微小变化，而如果这些变化小于预定义的截止距离，则在RP中无法检测到。因此，URP中的模式可以比RP提供更多的信息。为了从统计学角度量化URP，这里提出采用BGGMM进行URP统计定量分析方法，算法流程如下：

（1）输入时间序列x(t)；

（2）通过式（1）和式（2）经相空间重构获得无阈值递归矩阵Ri，j(unthres)，然后将递归矩阵中值的直方图进行归一化处理；

（3）初始化模型参数Θ=(ωj，μj，σj，λj)；

（4）通过式（10）式（14）迭代更新模型参数Θ；

（5）检测迭代收敛准则。若不满足，返回步骤（4）继续迭代，直至满足条件，迭代停止；

（6）输出均值和方差，组成特征向量(μ，σ)，对URP进行定量描述。

本节中，为了验证该方法的有效性，利用两组仿真信号进行分析。（1）周期信号：x(t)=sin(2π10t)；（2）Lorenz信号：

周期信号和Lorenz信号的时域波形图、对应的URPs以及归一化后的欧式距离分布直方图，如图1所示。从图1可看出，正弦周期信号URP的递归点沿主对角线平行或垂直分布，而混沌信号URP中出现大量平行与主对角线的线段。其对应的分布直方图近似服从于高斯分布，所不同的是，图1（a）中的直方图明显存在数据边界，数据也更加分散；图1（b）中，数据更接近于高斯分布，且相对集中，这表明原始信号存在差异。经BGGMM拟合（K=1），提取均值分别为1.45和1.92，方差分别为7.04和1.91，提取的均值和方差均存在差异，其中方差存在较大的差异也解释了直方图数据的集中程度的不同，这表明混合模型的参数可作为URP的定量分析指标。

图1 仿真信号时域图及其对应的URPs和欧式距离分布直方图Fig.1 Time-Domain Plot and their URPs as well as the Euclidean Distance Distribution Histogram of Simulate Signals

4 齿轮故障分类识别实验

这里将该方法应用于齿轮故障的分类，提出的齿轮故障分类算法的流程图，如图2所示。

图2 齿轮故障分类算法的流程图Fig.2 The Flowchart of Fault Classification Algorithm

4.1 实验装置

为了验证所提方法的有效性，通过齿轮故障实验台采集不同齿轮状态下的振动信号，实验台及其结构简图，如图3 所示。实验台包括550w（220V-50Hz）电机，带有一对啮合齿轮的齿轮箱，联轴器和磁粉制动器。其中，电机的转速和负载在（300～1217）r/min和（0～20）N·m范围内变动；小齿轮的齿数为20，大齿轮37，模数均为3；振动信号由安装在输入轴承座的垂直方向上的加速度传感器采集。

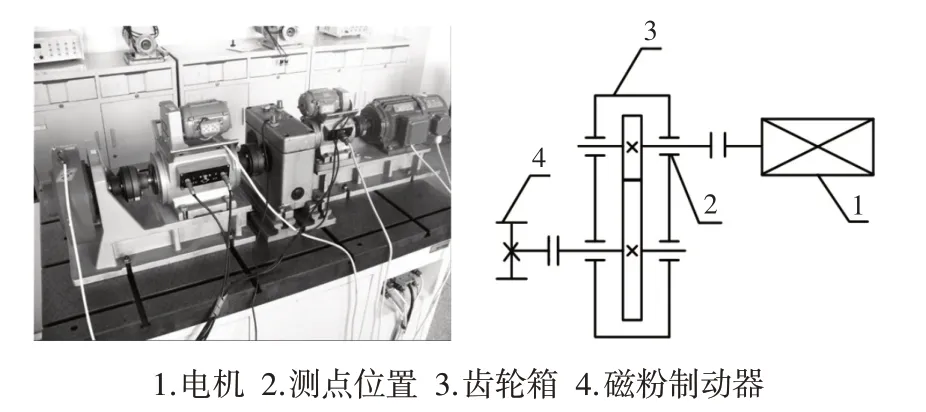
图3 齿轮故障实验台及其结构简图Fig.3 Gear Failure Test Table and its Structure Diagram

4.2 时域信号及无阈值递归图

采用上述实验台，分别采集四种齿轮状态的振动信号各100组，采样频率10kHz，采样时间0.1s。四种齿轮故障状态的时域信号波形图及其对应的URP，如图4、图5所示。原始信号不进行降噪处理，采用虚假邻域法确定嵌入维数d=4，平均互信息算法［16］确定延迟时间τ=4。

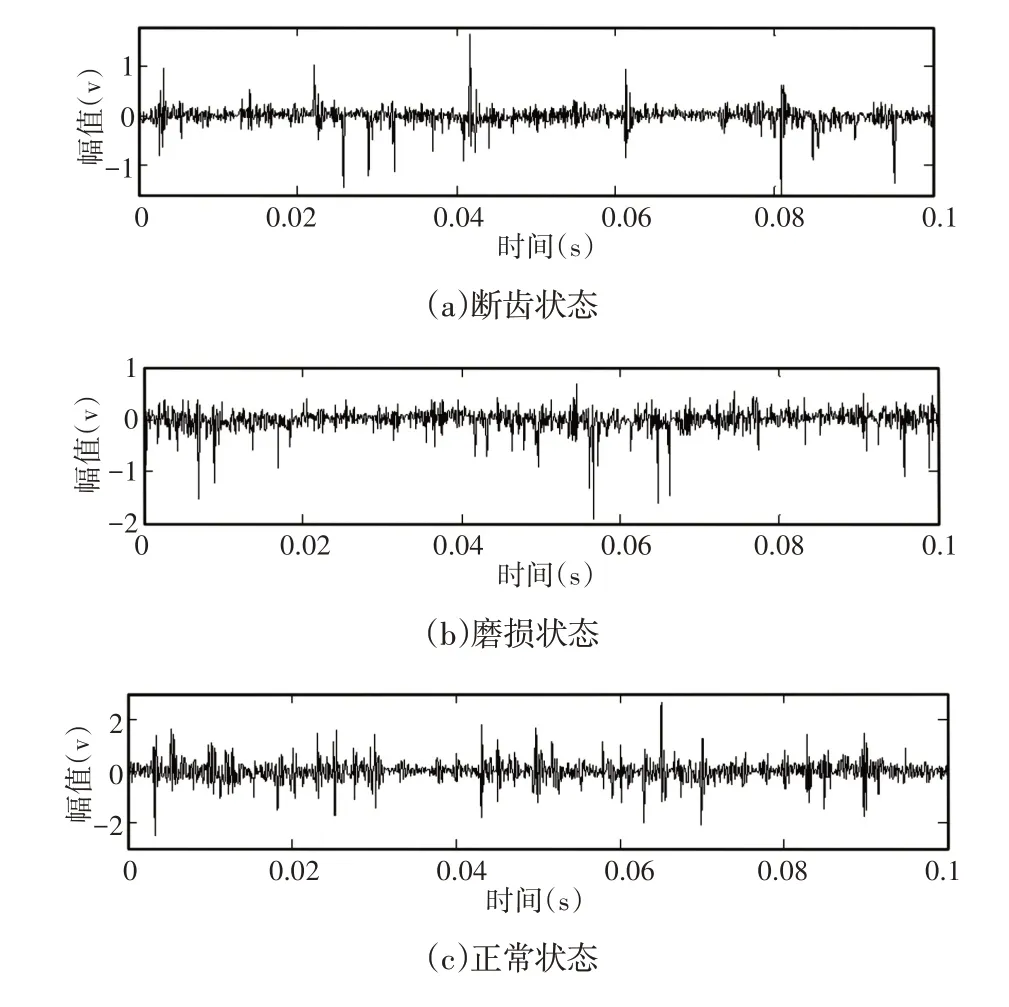
图4 四种齿轮状态时域波形图Fig.4 Time-Domain Signals of Four Gear States

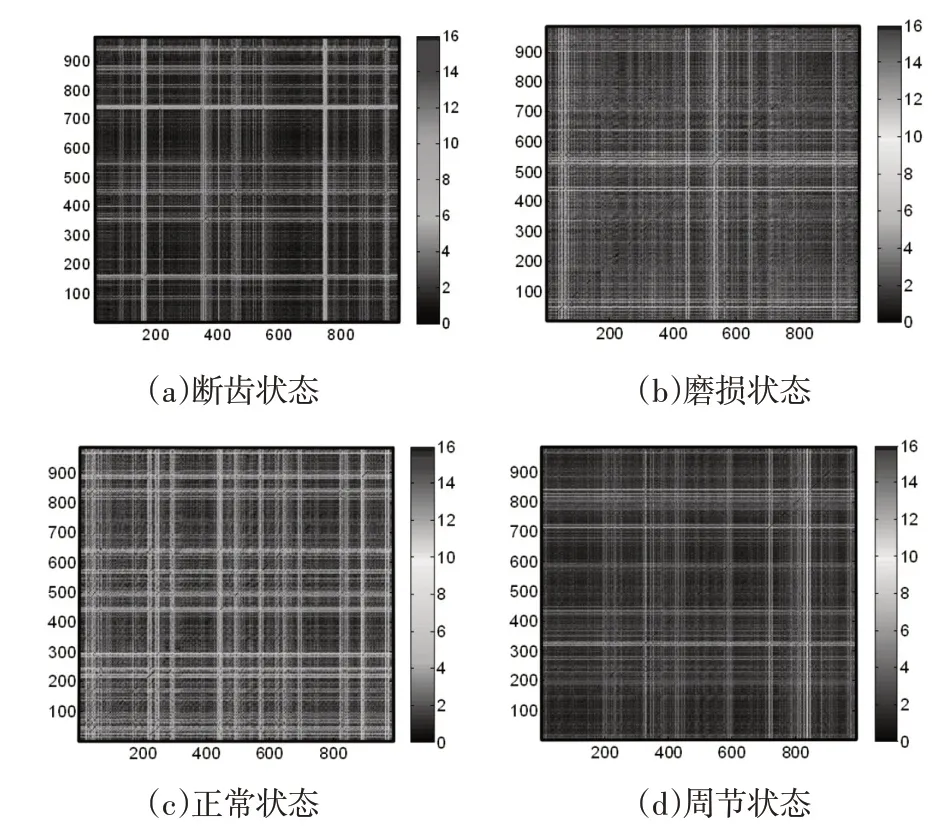
图5 四种齿轮状态的无阈值递归图Fig.5 Un-Thresholded Recurrence Plots of Four Gear States

从时域波形图看，原始信号掺杂噪声较多，无法直接从原始时域信号区分四种齿轮故障状态；从URP中看出，递归图中的递归点主要呈垂直分布，动力学系统所决定。

4.3 故障识别结果及对比

无阈值递归图中，向量之间的欧式距离大小由颜色深浅不一的递归点映射在图像中，如图5 所示。四种齿轮故障模式下的URP 颜色深度不同，表明递归点的欧式距离分布存在差异。应用BGGMM 拟合URP 中递归点欧式距离分布直方图，并提取均值和方差组成特征向量(μ，σ)用以齿轮的故障分类。分别以均值(μ)和方差(σ）为横纵坐标绘制，如图6 所示。由图6 可以看出，四种齿轮故障状态下的振动信号特征向量的分布存在较大的差异，除了断齿和周节两种状态存在少量重叠外，四种故障齿轮的特征向量基本完全被分开。

图6 BGGMM提取的特征向量分布情况Fig.6 Distribution of Feature Vectors Extracted by BGGMM

为了验证该方法的有效性，将所采集的各齿轮故障状态数据按1：1的比例分为训练数据和测试数据，即前50组数据用于训练，后50组数据用于测试，建立高斯混合模型，应用贝叶斯最大似然分类器进行分类。并与传统RQA的10种递归定量［16］（RR、DET、L、Lmax、ENTR、LAM、TT、Vmax、T1/T2）作为特征向量时的识别率进行比较，结果如表1所示。

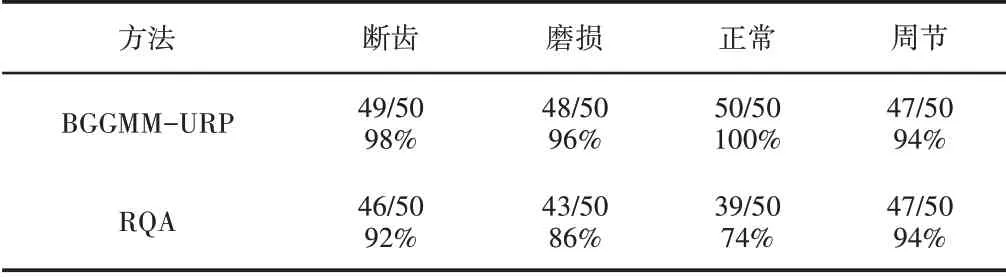
表1 URP定量分析和传统RQA方法的识别率Tab.1 Identification Rates of URP Quantitative Analysis and Traditional RQA Methods

从表1可以看出，基于BGGMM的URP定量分析方法的识别率明显高于传统RQA方法，四种齿轮故障状态的识别率均高于90%，其中对齿轮正常状态的识别率较高，达到100%。对于齿轮磨损和正常两种状态，较传统RQA 方法分别提高10%和26%。表明这里所提出的齿轮故障分类方法具有一定的优势。

5 结论

近年来，递归定量分析广泛应用于故障诊断等领域，但其诊断精度有待提高，此外，目前缺乏针对无阈值递归图定量分析的有效方法。这里提出一种采用BGGMM进行URP特征提取的方法，用于定量分析URP，并成功应用于齿轮的故障分类中。实验结果显示，与传统的RQA方法相比，该方法在齿轮故障识别方面具有更好的性能和更高的分类精度。

所提方法是从模式识别的角度，对无阈值递归图的一种统计定量分析方法，将递归矩阵中欧式距离的分布直方图的统计参数作为定量分析指标。但提出的定量指标所对应的动力学特征还需进一步研究，此外，研究其它的统计学参数作为定量分析指标也是后续的研究内容。