多子群社会群体优化算法的无人机航迹规划

2022-05-19项峻松

机械设计与制造 2022年5期

项峻松

（浙江交通职业技术学院，浙江杭州 311112）

1 引言

无人机可以在极端环境下进行高效作业，在军用和民用等领域得到广泛应用。无人机飞行航迹不仅影响其工作效率，而且对无人机飞行安全也有至关重要的影响［1］。因此研究无人机航迹规划具有重要的安全意义和经济意义。

无人机航迹规划是指在满足自身动力学约束、航程约束等约束条件下，规划出一条某种意义下最优的航迹［2］。无人机航迹规划可分为节点生长类方法和智能算法类规划方法，节点生长类方法是以航迹起始点为始节点，不断向目标点生长从而规划出航迹，包括A*算法、Dijkstra算法等，文献［3］将航迹规划分为静态规划和动态规避两个步骤，动态规避航迹使用A*算法的节点生长方法；文献［4］在元细胞环境模型下，使用改进D*算法进行路径规划，与D*算法相比减少了转弯次数和规划时间。智能算法类规划方法，通过建立模型将航迹规划问题转化为寻优问题，包括人工鱼群算法［5］、人工蜂群算法［6］、粒子群算法［7］等。智能算法类航迹规划质量主要受两方面影响，一是模型精度，二是智能算法的性能。

这里以二维环境下无人机航迹规划为研究对象，建立了威胁模型和航迹规划模型，提出了多子群社会群体算法的规划方法。在社会群体算法基础上，将个体分为多个子群，通过对提高阶段和获得阶段改进、子群间信息交流，实现了提高算法种群多样性和寻优能力的目的，最终规划出航程短且安全性高的航迹。

2 威胁分析及规划模型

2.1 航迹生成方法

这里研究内容是无人机在二维环境下的航迹规划问题，此时无人机在定高度飞行，或飞行高度起伏不大。为了简化轨迹表达方法，这里直接将坐标系的OX轴建立在起点与终点连线上，然后将起始点与目标点间的线段等分成N段，只需规划出各等分点处的纵坐标值（y值）就实现了航迹规划，如图1所示。

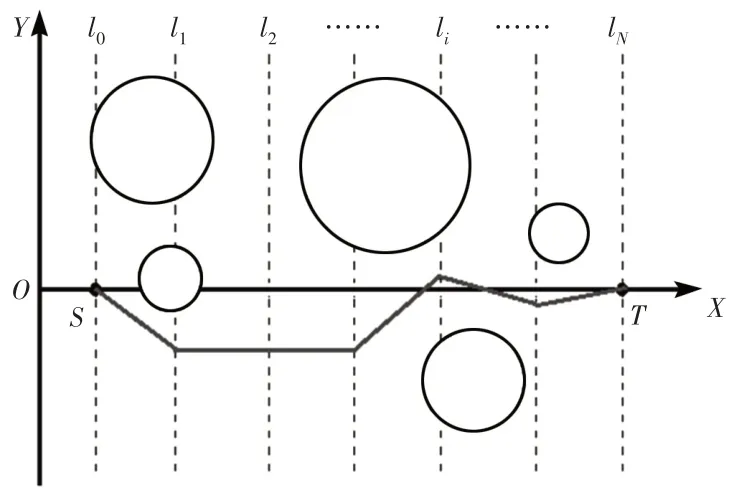
图1 航迹生成方法Fig.1 Route Generating Method

2.2 威胁分析

无人机在特定高度飞行时，可能遭受的威胁包括山体等障碍物的碰撞威胁、雷达的探测威胁、导弹火炮等的打击威胁等，下面具体分析。

（1）雷达的探测威胁。在理想情况下，雷达的探测范围是一个半球形，但是考虑到雷达的探测角限制，雷达的实际探测范围是一个近似圆锥形。在特定高度上，雷达探测范围可视为圆形［8］，即：

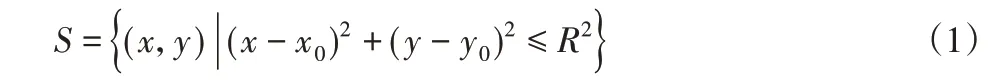
式中：R—圆形探测区域半径，半径大小根据探测能力确定。

雷达通过接收探测无反射的回波捕捉目标，捕获概率与回波质量有关，雷达接收的回波功率为：

式中：Pr—雷达接收功率；Pt—雷达发出功率；Gt—发射天线增益；λr—雷达波长；σr—被探测目标反射面积；Ft—传播因子；dr—目标与雷达间距离，且为无人机飞行高度；drt—飞行面内无人机与雷达距离。

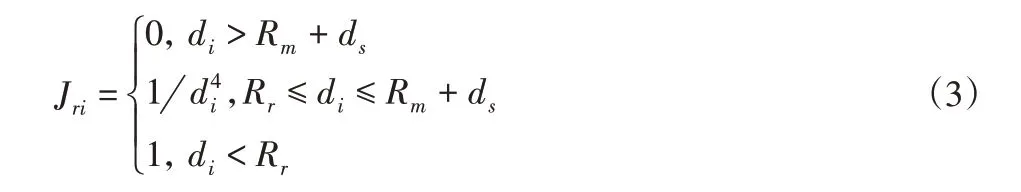
（2）导弹的打击威胁。导弹的对空打击具有最小攻击角和最大攻击角限制，从三维看，类似于中空的圆锥形，在特定高度的二维平面上，导弹打击范围为一个圆环，如图2中阴影部分所示。圆环的内半径r与外半径R由最大最小攻击角及飞行高度确定。

图2 导弹打击区域Fig.2 Missile Striking Area

导弹对无人机的命中概率与两者间的距离无直接关系，只要无人机在导弹攻击范围内，命中概率与导弹的性能具有直接关系，因此为了保证无人机的绝对安全，这里将导弹打击区域设置为禁飞区，即第i条航迹li受导弹打击威胁为：

式中：Jsi—第i条航迹受的打击威胁；

Rs—导弹打击区域的外半径；

di—第i条航迹li与导弹的最短距离。

（3）障碍物威胁。无人机飞行过程中的障碍物包括山体、高楼等，高楼的二维投影图一般为方形，因此根据投影图尺寸使用方形表示高楼障碍物。对于单山峰地形，山体在特定高度的截面类似于圆形，因此使用圆形代表山体障碍物。将障碍物对无人机威胁设置为无穷大，即无人机航迹必须完全避开障碍物区域，在实际操作时，将障碍物威胁取为较大值，则第i条航迹li受障碍物威胁为：

式中：Sobs—障碍物区域；

M—较大常值，可取为100。

综合以上分析，无人机在整个飞行过程中受到的雷达探测、导弹打击、障碍物等的综合威胁J为：

式中：N—航迹段数量。

2.3 航迹规划目标函数

航迹规划的目标是在满足无人机转弯、航程等约束条件下，规划出一条飞行安全、航程最短的航迹。按照图1的航迹生成方法，得到航迹长度为：

式中：li—第i条航迹的长度。

由式（6）和式（7）得到航迹规划的目标函数为：

式中：w1、w2—安全系数和航程系数，其作用是：（1）调节两优化指标处于同一数量级；（2）调节优化重心，通过取值不同得到不同侧重点的优化结果。

2.4 约束条件分析

对于二维环境下的无人机航迹规划，其约束条件包括航程约束和转弯角约束。

2.4.1 航程约束

由于无人机携带的燃料有限，在进行航迹规划时，从起点至终点的航迹长度不能超过无人机最大航程，记无人机最大航程为lmax，则：

2.4.2 转弯角约束

这里指出，规划出航迹纵坐标{y1，y2，…，yN-1} 后使用B 样条均值曲线对航迹进行平滑处理，若使用等分点处的转弯角给出约束条件则有些不符合实际情况，这里使用等分点处的转弯半径进行约束，记无人机的最小转弯半径为rmin，则：

式中：ri—各等分点处的转弯半径。

3 多子群社会群体优化算法

通过第2节的建模过程，将航迹规划问题转化为带约束条件的优化问题，本节提出了多子群社会群体优化算法用于求解此优化模型。

3.1 社会群体优化算法

当个体能力不足以解决复杂问题时，个体需要向周围其他个体或拥有此能力的个体学习，社会群体优化算法就是基于这一思想提出的，包括种群初始化、提高阶段、获得阶段三个步骤完成［9］。

3.1.1 种群初始化

记种群规模为D，使用随机方式初始化种群，为：

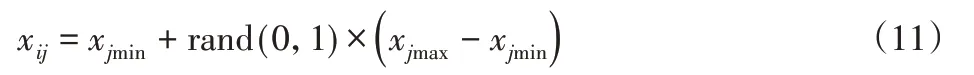
式中：xij—第i个个体在第j维上的取值，i=1，2，…，D，j=1，2，…，N-1；xjmax、xjmin—j维上最大值和最小值；rand(0，1)—（0，1）上的随机数。

3.1.2 提高阶段

在提高阶段，个体向群体最优学习，从而获得解决问题的能力，方法为［10］：

式中：c∈(0，1)—自我反省参数，其经验值为c=0.2；gbestj—最优个体在第j维上的取值。

3.1.3 获得阶段

在获得阶段，从种群中随机选取一个个体作为学习对象，并结合全局最优信息对自身位置更新，方法为［10］：

若个体i优于个体k，则位置更新方法为：

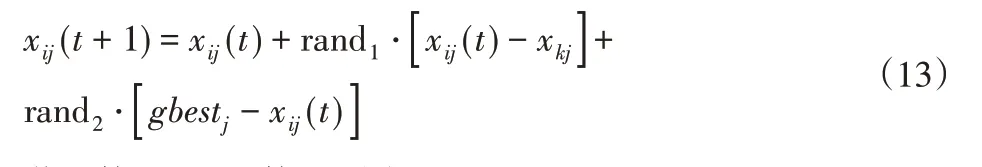
若个体i劣于个体k，则位置更新方法为：

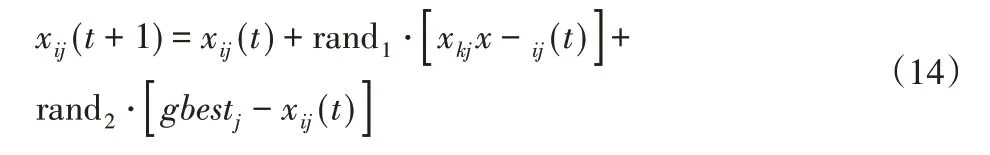
式中：rand1、rand2—（0，1）间的随机数。

3.2 多子群社会群体优化算法

由3.1节可以看出，在算法的提高阶段和获得阶段，个体均向当前最优个体学习，这种单目标或单向学习方式虽然能够加速算法收敛，但是严重破坏了种群多样性，极易导致算法早熟，尤其当前最优为局部极值时，会引导算法陷入局部最优。为了改善算法搜索过程中的种群多样性，提出了多子群社会群体优化算法。首先按照等分原则，将D个个体等分为E个子群，不能等分时，将多余粒子随机分配到若干子群中。

3.2.1 改进提高阶段

在多子群算法中，提高阶段按照就近向“好同学”学习的原则，向子群最优个体学习，使其在局部区域内获得能力增长，为：

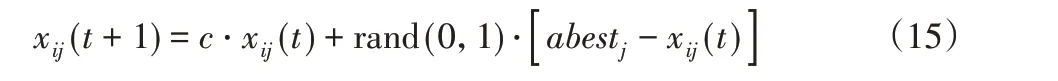
式中：abestj—子群a最优个体在j维上的取值。

3.2.2 改进获得阶段

为了兼顾学习范围的局限性和学习方法的多样性，在知识获得阶段，提出三种知识来源：一是子群内其他个体，二是任意子群的最优个体，三是整个种群的最优个体。这种多渠道知识获取方法和学习方法，对提高种群多样性具有重要意义。基于以上思想，个体i的学习和更新机制为：

若个体i优于个体k，则：

若个体i劣于个体k，则：

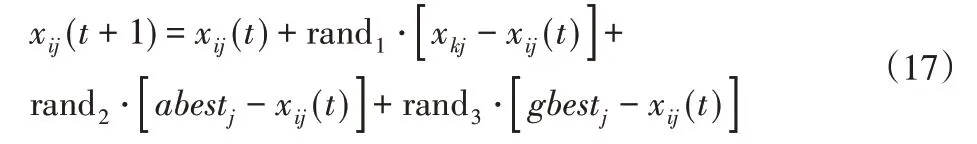
式中：xkj—与个体i处于同一子群内的个体k在j维上的取值；abestj—任意子群a的最优个体在j维上的取值；gbestj—种群最优个体在j维上的取值。

3.2.3 子群重组与信息交流。

算法搜索过程中只关注最优个体，而不关注种群均值，因此算法改进应倾向于增加种群多样性使种群在搜索区域较为平均地分布。随着算法的迭代进行，个体必然向较优区域靠拢，就导致个体聚集度越来越高而多样性越来越差，为了维持种群多样性，每当算法迭代一定次数后，将子群重新随机分配，分配方法依然使用等数量随机分配。记子群重新分配的迭代周期为T，T越大有利于种群收敛，T越小有利于种群多样性。

3.3 多子群社会群体优化算法流程

根据3.2节对多子群社会群体优化算法的描述，制定算法流程，如图3 所示。图中：iter—当前迭代次数；mod—取余函数；itermax—最大迭代次数。

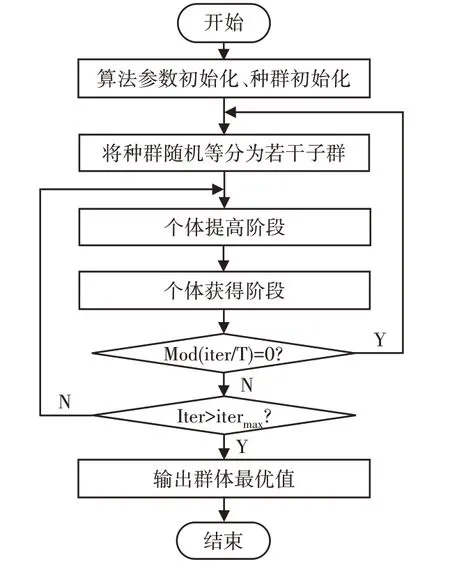
图3 多子群社会群体优化算法流程Fig.3 Multiple Subgroups Social GroupOptimizing Algorithm Flow

4 仿真验证与分析

本节对两个方面的内容进行验证：（1）验证多子群社会群体优化算法的多样性和寻优性能；（2）验证多子群社会群体优化算法在航迹规划中的性能。

4.1 多子群算法的种群多样性和性能测试

种群多样性的计算方法有多种，包括所有个体的平均汉明距离、所有个体与群体中心距离之和、所有个体与群体中心距离熵等，这里使用平均汉明距离计算种群多样性。

种群中个体pi与pl间的距离H(pi，pl)为：

两者的归一化距离为：

所有个体的平均汉明距离为：

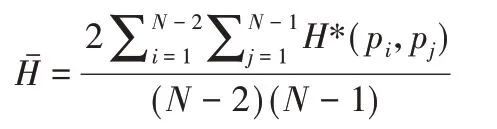
多子群社会群体优化算法参数设置为：种群规模D= 50，子群规模为10，算法最大迭代次数为400，选择标准测试函数中的Schwefel 函数和Rotated Schwefel 函数进行性能测试，两函数维度均设置为50，自变量变化范围为［-500，500］，在此范围内的函数最小值均为0。两种算法对两种测试函数均独立运行30次，随机选择某次算法迭代过程中，种群多样性变化过程，如图4所示。

图4 迭代过程中种群多样性测试Fig.4 Population Diversity Test in the Iteration Process

从图4中可以看出，对Schwefel函数寻优时，在前30次迭代过程中，社会群体算法的种群多样性急剧下降，而多子群社会群体算法的种群多样性虽然经历了下降过程，但是经过子群重组和信息交流，种群多样性又恢复到较高水平。对Rotated Schwefel函数的寻优过程中，多子群社会群体算法的种群多样性也保持较高水平，总体上远远大于社会群体算法，说明这里的改进措施对增加算法的种群多样性具有明显效果。

两种算法对两种基本测试函数的寻优结果，如表1所示。

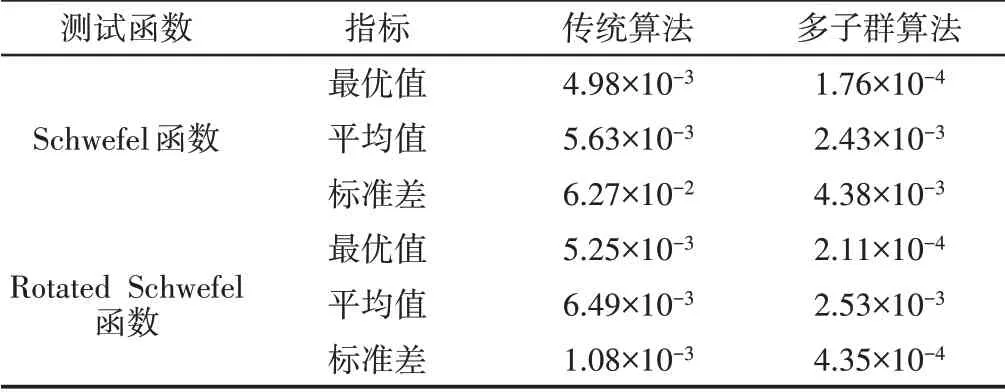
表1 测试函数的寻优结果Tab.1 Optimizing Result of Different Testing Function

由表1可以看出，通过增加物种多样性的方式提高了算法的最优解精度，相比于传统的社会群体算法，多子群算法搜索的测试函数最优解均提高了一个数量级，但是寻优结果的平均值相差不大，这是因为通过增加种群多样性，使个体在搜索空间较为均匀的分布，必然会留有较多劣质解拉低平均值。这里只关注种群中的最优解，因此多子群社会群体算法的寻优能力远远优于传统算法。而且从方差上看，多子群算法的寻优稳定性优于传统算法。

4.2 航迹规划结果及分析

为了验证多子群社会群体算法在航迹规划中的性能，使用MATLAB R2014a软件进行仿真实验。算法种群规模D=50，子群规模为10，算法最大迭代次数为400。无人机飞行环境设置在（100×100）km2区域内，起点为（10km，10km），目标点为（90km，90km）。航迹等分点数设置为N=21，航迹点搜索范围为［0，100km］。环境中的威胁设置，如表2所示。

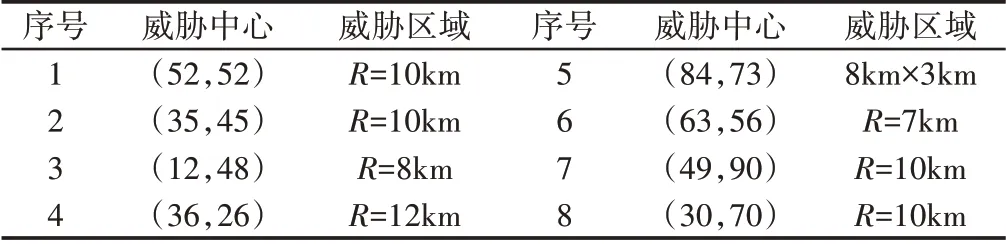
表2 威胁分布情况Tab.2 Distribution of Every Threaten

分别使用社会群体优化算法和多子群算法规划从起始点到目标点的航迹。两种算法各独立运行20次，挑选出两种算法各自的最优航迹结果，如图5所示。图中阴影覆盖的圆形威胁为山体，阴影覆盖的方形威胁为建筑物，其余圆形威胁为雷达、导弹威胁等。实线为使用多子群社会群体算法规划的航迹，虚线为使用传统社会群体算法规划的航迹。

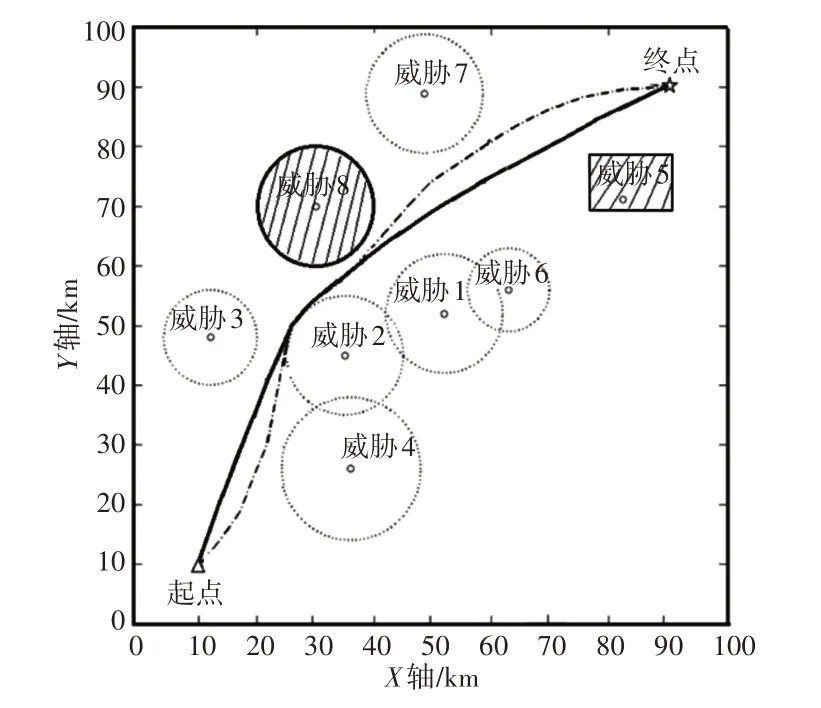
图5 不同算法规划的航迹Fig.5 Route Planned by Different Algorithm

由图5可以看出，多子群算法规划的航迹明显短于传统算法规划的航迹，从受威胁程度看，两个航迹在威胁2边沿处转弯时受的威胁最大，航迹其余段均绝对安全。经统计，传统算法在迭代至100代时适应度不再下降，搜索的目标函数值为103.25；多子群算法在算法迭代至40代时搜索到最优值，目标函数最优值为96.38，相比于传统算法减少了6.65%。综合图5和统计数据可知，多子群社会群体算法规划的航迹长度和安全性方面均优于社会群体算法规划的航迹，且算法完成收敛的迭代次数大大减少，这是因为多子群算法将个体分为多个子群，通过对提高阶段、获得阶段进行改进，使个体通过多渠道获得知识，实现了学习方式多样性；而且通过子群重组实现了子群间的信息交流，维持了算法在整个迭代过程中的种群多样性，最终实现了提高算法搜索能力的目的。