基于OpenFOAM的礁坪上波浪底部切应力数值模拟研究
2022-05-19李岩汀胡乾明刘清君孙天霆王登婷
黄 哲,李岩汀,胡乾明,刘清君,孙天霆,王登婷*
(1.南京水利科学研究院,南京 210024;2.水文水资源与水利工程科学国家重点实验室,南京 210029;3.河海大学 港口海岸与近海工程学院,南京 210098)
礁盘地形通常由陡峭的礁前斜坡和水深较浅的礁坪组成,波浪在礁缘或礁坪上传播会发生剧烈的变形和破碎。波浪破碎区是泥沙起动及物质输运的重要区域,因此,开展该区域床面切应力研究,分析底部切应力随水深、入射波高和波周期等因素变化规律,对于研究礁盘地形上的生态环境和地形演变具有重要的科学和现实意义。
目前,关于床面切应力的研究多采用物理模型试验的手段。Mirfenderesk[1]使用应力板分别测量了光滑和粗糙床面的波浪床面切应力。Seelen[2]使用应力板测量了孤立波作用下的床面切应力。Arnskov[3]使用热膜探针测量了波、流共同作用下的床面切应力。Tanaka[4]应用嵌平式热膜探针在波浪水槽内测量了椭圆余弦作用下层流边界层内床面切应力。徐华等[5]采用柔性热膜式壁面切应力传感器测量了波、流共同作用下床面切应力。郝思禹[6]在坡度1:5的斜坡上开展了切应力模型试验研究,发现波浪破碎前后切应力具有较大差异。刘清君[7]对岛礁地形上礁缘处和礁坪后方波浪稳定区床面切应力进行了研究。黄海龙[8]研究了完全直接测量二维波浪和水流共线作用时床面切应力仪的设计和制作。
关于床面切应力的数值模拟研究一般通过计算区域流场或紊动场,然后根据流速与切应力之间关系计算得到底部切应力,常见计算方法有二次阻力律法、对数拟合流速剖面法等。Jonsson[9]提出波浪摩阻系数定义式,通过边界层外近底最大自由流速计算床面切应力。Cox[10]在此基础上引入近底床面瞬时流速,建立了瞬时床面切应力二次阻力律公式。张庆河[11]通过对大量波浪边界层和床面切应力数据进行分析,建立了可用于波浪作用下层流和紊流边界层床面摩阻系数计算式。流速剖面法假定近底流速沿水深近似满足对数分布,通过近底区域内流速拟合得到摩阻流速,在通过摩阻流速计算床面切应力[12]。Yuan等[13]在振荡水槽中对比各种计算床面切应力计算方法,认为流速剖面法准确性最好。
结合国内外研究情况,以往波浪底部切应力的研究大都集中于平底地形或单一的斜坡地形,针对复合地形的试验测点布置较少,不足以分析波浪底部切应力在礁盘地形上的沿程变化规律[7]。为此,本文基于OpenFOAM开源代码中两相流求解器OlaFlow建立礁盘地形的数值波浪水槽,对礁盘地形上的波浪传播进行数值模拟,分析水深、入射波高和波周期对礁坪上波浪底部切应力沿程变化的影响。
1 数学模型
1.1 控制方程
OpenFOAM中OlaFlow两相流求解器采用的控制方程为三维VARANS方程
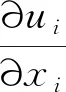
(1)
(2)
式中:ui为xi方向的速度分量;ρ为流体密度;t为时间;p*为动压力;g为重力加速度;Xj为控制体中心点的位置分量;μtot为有效动力粘度系数,μtot=μ+μt,μ为粘度系数,μt为紊动粘度系数,取决于所选用的紊流模型。
采用SSTk-ω紊流模型[14]确定VARANS方程中的紊动粘度系数μt,具体如下
(3)
(4)
(5)
式中:k为紊动动能;ω为紊动能耗散率;S为应变率张量;F1、F2为混合函数;紊流模型中各参数取值如下:β*=0.09,α1=5/9,β1=3/40,α2=0.44,β2=0.082 8。
1.2 造波和消波边界
在计算域入口使用速度入口边界条件[15],速度入口边界条件通过设定波面和流体速度进进行造波。根据LeMehaute波浪理论适用范围[16],结合本文所模拟的波浪要素,采用二阶斯托克斯波理论进行造波。在计算域入口和出口处设置主动消波边界[17]进行消波,消波边界通过产生与入射波速度相同方向相反的速度进行消波。主动消波方法相比于松弛域消波或多孔介质消波等被动消波方法,可以显著减小计算域大小,节省计算资源。
1.3 固壁边界及底部切应力
数值水槽中一般将固壁边界设为不可滑移边界条件,但这样规定边界条件就必须将微分方程对黏性底层积分。由于黏性底层中的流速梯度很大,为了得到理想的数值解,必须在近壁面区域布置极细密的网格,极大的增加了计算成本,也容易造成网格畸形导致计算发散。为了解决上述问题,模型中引入壁面函数,建立了近壁面网格点至壁面之间的流速非线性变化模型。底部切应力可以利用切应力的定义式并结合壁面函数求出。
壁面切应力按式(6)计算,式中的系数vnew由式(7)确定。
(6)
(7)
式中:uc为靠近壁面第一层网格中心点平行于壁面的流速;uw为壁面上的流体速度,可取0;κ为卡门常数,取0.41;E为常数,取9.8;y+为靠近壁面第一层网格中心点到壁面的无量纲垂直距离。
1.4 数值方法
OpenFOAM使用有限体积法进行离散求解。本文各控制方程中,时间导数项采用隐式欧拉格式,梯度项采用高斯线性插值,对流项采用Gauss limited Linear V1格式,拉普拉斯项采用高斯线性修正格式,速度压力耦合方程采用PIMPLE(PISO-SIMPLE)算法求解。PIMPLE算法是将单个时间步长内流动看作是稳态流动使用SIMPLES算法进行求解,在时间步进上采用PISO算法进行求解。
2 数值模型建立与验证
2.1 数值模型建立
假定礁盘地形为梯形平台,平台高0.5 m,迎浪斜坡坡度为1:1,右侧礁坪长度为8 m,礁盘总长8.5 m。
礁盘地形数值波浪水槽网格及边界条件示意图见图1。水槽长14 m,宽1 m,高1 m,礁盘坡脚设置在距离造波边界3倍波长处。为能够精确捕捉自由水面和避免波浪沿程衰减,在静水面上下3倍波高范围内对网格进行加密,加密后的网格长度小于波长的1/300,网格高度小于波高的1/20。同时,为适应壁面函数边界条件的要求,对礁坪上近壁面0.01 m范围进行网格加密,加密后网格长度和高度均为0.002 5 m。为保证计算的稳定性和收敛性,计算时间步长的选取应使得Courant数小于1,本文取波周期的1/1 000。

图1 数值域网格及边界条件设置Fig.1 Numerical grides and boundary condition of the numerical domain
2.2 计算工况
数值计算中考虑波周期、波高和礁坪上相对水深对波浪底部切应力的影响,试验波浪采用规则波,波高选取0.05 m、0.06 m、0.07 m和0.08 m,波周期选取1.0 s、1.5 s、2.0 s和2.5 s,礁前水深选取0.6 m、0.65 m、0.7 m和0.75 m,不同参数之间进行组合,共计10组计算工况。
2.3 模型验证
利用礁盘地形上波浪传播物模试验结果[7],通过波面过程线、最大平均流速沿水深分布和底部切应力等方面对比,验证所建礁盘地形数值波浪水槽模型。
(1)波高验证。
参考模型试验中波高测点位置,在数值模型中分别选取距离坡脚0.5 m、1.0 m、2.0 m、6.5 m的4个测点,给出波浪历时曲线对比图,如图2所示。图中可以看出,波高过程计算值与实测值吻合良好,表明该模型能够有效地模拟波浪在礁盘地形上的浅水变形和波浪破碎。
(2)断面流速验证。
为了进一步验证模型的合理性,分别对断面最大平均流速沿水深分布进行了验证。其中断面最大平均流速选取距离坡脚1.3 m和2.3 m两个断面,测点水深分别为-0.2h2、-0.4h2、-0.6h2、-0.73h2和-0.95h2,流速验证情况如图3所示,其中向岸为正,离岸为负。

X=0.5 m X=1.0 m

X=2.0 m X=6.5 m2-a H=0.05 m

X=0.5 m X=1.0 m

X=2.0 m X=6.5 m2-b H=0.07 m

X=1.3 m X=2.3 mX=1.3 mX=2.3 m3-a H=0.05 m3-b H=0.07 m
图3中可看出,向岸和离岸的最大平均流速沿水深均存在不同程度的衰减,向岸流的衰减幅度大于离岸流。且随着波高的增大,向、离岸最大流速分布相对0值位置的不对称性明显较大,流速分布整体向正方向偏移。数值模拟研究可以较为准确地反映出这一现象及沿程不同水深处的流速分布规律。
(3)底部切应力验证。
底部切应力验证选取的两个测点分别位于距离坡脚0.6 m和4.0 m处,图4给出了剪切力随时间的变化对比图,图中向岸切应力为正,离岸切应力为负,切应力计算值与实测值吻合较好,极值较为接近。

X=0.6 m X=4.0 m4-a H=0.05 m

X=0.6 m X=4.0 m4-b H=0.07 m
3 数值计算结果分析
为了分析波浪底部切应力在礁坪上的沿程变化,从礁缘处开始,每隔0.5 m设置数据采集点,用于采集流速和紊动粘性系数,然后通过计算得到底部切应力。
3.1 礁坪上相水深对底部切应力影响
礁坪上相对水深△(△=h2/h1)是影响礁坪上波浪破碎和底部切应力的重要因素,其中h2为礁坪上水深,h1为礁前水深。
图5反映了入射波要素为H=0.06 m,T=1.0 s时,不同△条件下向岸和离岸切应力沿程变化情况。整体来看,向岸和离岸切应力均随着△的减小而呈现出增大趋势,主要原因是随着△的减小,波浪传播受礁盘地形影响增大,波浪发生浅水变形,波峰变得尖陡而波谷变得平坦,非线性效应逐渐增强,当波高达到破碎值后波浪发生破碎,产生的紊动水体会扩散并影响近底流速,进而引起切应力增大。
图5中向岸和离岸切应力在礁坪上的沿程变化情况可以看出,当△较大时,向岸和离岸切应力在礁坪上沿程变化幅度相对较小,而随着△的减小,切应力沿程变化幅度增大。结合△=0.17时切应力沿程变化情况可见,向岸和离岸切应力均随与礁缘间距离的增大呈现先增大后减小的趋势,且在礁缘处的4倍波长左右(X=1.5 m)达到峰值,主要是由于波浪传播至该处时发生卷破,水舌投入水中后引起水体发生剧烈紊动,导致离岸和向岸切应力增大。
波浪在礁坪上部传播一段距离后趋于稳定,除△=0.23,其他△工况下,稳定后的切应力大小相近,表明礁坪上水深对波浪稳定后的底部切应力影响相对较小,其值一般由入射波浪条件控制。
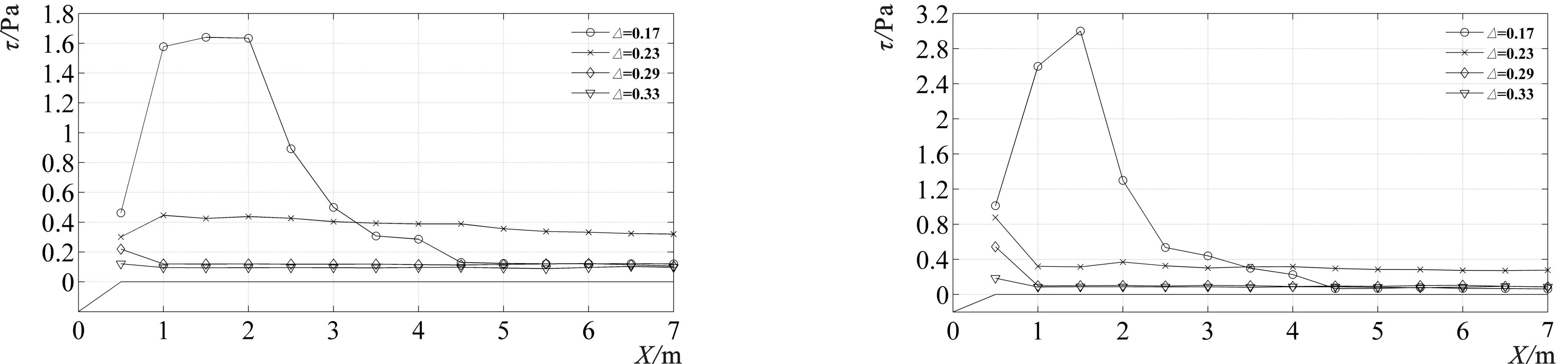
5-a 向岸切应力 5-b 离岸切应力图5 沿程切应力随相对水深变化(H=0.06 m,T=1.0 s)
3.2 入射波高对底部切应力影响
入射波高作为波浪的重要参数,是波浪在礁坪上变形与破碎的重要影响因素,图6为△=0.23,周期1.0 s时,不同入射波高条件下,向岸和离岸切应力沿程变化图。
总体上看,向岸和离岸切应力均随着入射波高的增加而增大。向岸切应力最大值大都出现在X=1.0 m附近,而离岸切应力主要出现在礁缘处,且离岸切应力的最大值约为向岸切应力的2.5倍至3倍。这是由于向岸切应力主要受波高影响,波浪传播至礁坪上发生破碎,破碎点处波高增加,使得向岸切应力增加,而离岸切应力主要由波谷作用时离岸回流引起,波谷传播至水深突变的礁缘处水体回落,会在礁缘处产生剧烈的离岸流。

6-a 向岸切应力 6-b 离岸切应力图6 沿程切应力随入射波高变化(T=1.0 s,h2=0.15 m)
图6-a中,不同入射波高对波浪稳定后切应力有一定影响,入射波高越大,向岸切应力越大,而图6-b中,不同波高稳定后离岸切应力差别相对较小,入射波高对稳定后离岸切应力几乎无影响。
3.3 入射波周期对底部切应力影响
图7为不同波周期条件下,向岸和离岸切应力沿程变化关系图。
图7-a可见向岸切应力最大值出现在礁缘后方破波点附近。随着入射波周期的增加,礁坪上最大切应力增大且最大值所在位置向礁缘后方移动。在X>7.5 m之后,向岸切应力沿程增加,这是因为波浪破碎后会形成段波向后方传播,行进波的形成影响近底流速,使向岸切应力增加。图中可以看出波周期越大,稳定后的向岸切应力也越大。
由图7-b可见,离岸切应力在礁缘处达到最大值后迅速衰减,不同于向岸切应力,离岸切应力在礁坪上保持沿程衰减,在波浪传播达到稳定后,大周期波浪相应的离岸切应力略大,但不同周期下波浪稳定处的切应力差值整体较小。
综上可见,周期对稳定后的向岸切应力影响大于离岸切应力。

7-a 向岸切应力 7-b 离岸切应力图7 沿程切应力随入射波周期变化(H=0.06 m,h2=0.15 m)
4 结论
本文基于OpenFOAM中两相流求解器OlaFlow建立礁盘地形数值波浪水槽,对礁盘地形上波浪传播进行数值模拟,分析了相对水深、入射波高和波周期对礁坪上的波浪底部切应力沿程变化的影响,得到主要结论如下:
(1)礁坪上向岸和离岸切应力随相对水深的减小而增大,随入射波高和入射波周期的增大而增大;
(2)礁坪上波浪稳定后的向岸底部切应力随入射波高和入射波周期的增大而增大,受相对水深影响较小。
(3)礁坪上波浪稳定后的离岸底部切应力受入射波高、入射波周期和相对水深影响均较小。
(4)向岸切应力最大值主要出现在礁缘后方,随入射波周期增大,向岸切应力最大值出现位置向礁缘后方移动;离岸切应力最大值主要出现在礁缘处。
