导数在双变量函数中的应用赏析

■安徽省霍邱县第一中学 陈仿云 余其权(特级教师)

一、结构统一,构造函数

例1(2022届深圳市实验学校月考)已知函数f(x)=,g(x)=alnx。

(1)若曲线y=f(x)-g(x)在x=2处的切线与直线x+3y-7=0垂直,求实数a的值;

(2)设h(x)=f(x)+g(x),若对任意两个不等的正数x1,x2,都有＞2恒成立,求实数a的取值范围。

解析:(1)由y=f(x)-g(x)=-alnx,得y＇=x-。

(2)h(x)=f(x)+g(x)=+alnx。

因为对任意两个不等的正数x1,x2,都有＞2 恒成立,设x1＞x2,则h(x1)-h(x2)＞2(x1-x2),即h(x1)-2x1＞h(x2)-2x2恒成立。

令F(x)=h(x)-2x,则问题等价于函数F(x)=+alnx-2x在(0,+∞)上为增函数,所以F＇(x)=x+-2≥0在(0,+∞)上恒成立,即a≥2x-x2在(0,+∞)上恒成立,即a≥(2x-x2)max=1。

故实数a的取值范围为[1,+∞)。

二、寻找关系,变量化一

例2(2022届阳春市第一中学月考)已知函数f(x)=x2+ax+2lnx(a为常数)。

(1)当a≤4时,讨论函数f(x)的单调性;

(2)若f(x)存在两个极值点x1,x2,且|x1-x2|≤,证明:|f(x1)-f(x2)|≤-4ln 2。

解析:(1)因为f(x)=x2+ax+2lnx,x∈(0,+∞),所以f＇(x)=2x+a+。

设g(x)=2x2+ax+2,x∈(0,+∞)。

当-4≤a≤4时,Δ≤0,2x2+ax+2≥0成立,则有f＇(x)＞0,所以函数f(x)在(0,+∞)上单调递增。

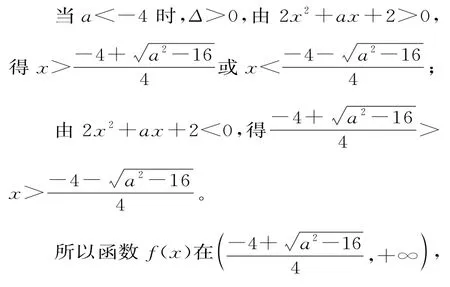
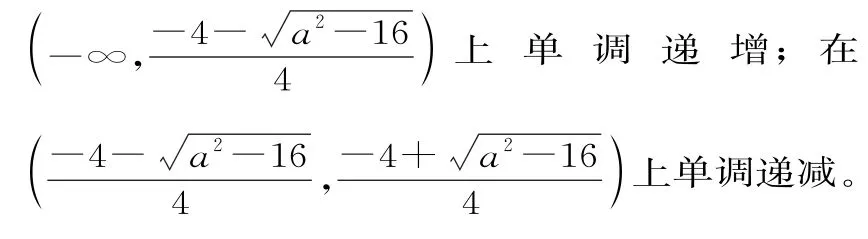
(2)由(1)知函数f(x)的两个极值点x1,x2满足2x2+ax+2=0,所以x1·x2=1,x1+x2=。

不妨设0＜x1＜1＜x2,则f(x)在(x1,x2)上是减函数,故f(x1)＞f(x2)。

评注:本题的关键点为利用函数的两个极值点求得x1,x2的关系,利用函数的单调性求得|f(x1)-f(x2)|=f(x1)-f(x2),代入解析式替换掉x1后得到仅含有一个变量x2的解析式,然后构造函数求导,利用单调性解决问题。

三、差的代换,变量化一

例3(2021 届湛江市高三第一次模拟)已知函数f(x)=ex,g(x)=2ax+1。

(1)若f(x)≥g(x)恒成立,求a的取值集合;

(2)若a＞0,且方程f(x)-g(x)=0有两个不同的根x1,x2,证明:＜ln (2a)。

解析:(1)令u(x)=f(x)-g(x)=ex-2ax-1,则u＇(x)=ex-2a。

若a≤0,则u＇(x)＞0恒成立,u(x)在R上单调递增,又因为u(0)=0,当x＜0 时,u(x)＜0,不合题意,故舍去。

若a＞0,令u＇(x)=0,得x=ln(2a),故当x＜ln(2a)时,u＇(x)＜0,u(x)单调递减;当x＞ln(2a)时,u＇(x)＞0,u(x)单调递增。故u(x)max=u(ln(2a))=2a-2aln(2a)-1≥0。

令h(x)=x-xlnx-1,所以h＇(x)=-lnx,令h＇(x)=0,得x=1,故h(x)在(0,1)上单调递增,在(1,+∞)上单调递减,故h(x)≤h(1)=0,即h(x)=x-xlnx-1≤0,即2a-2aln(2a)-1≤0,故2a=1,即a=。

综上可得,a的取值集合为。

(2)方程f(x)-g(x)=0有两个不同的根x1,x2,不妨令x1＜x2。

令t=＞0,即证e2t-1＞2tet,令g(t)=e2t-1-2tet,则g＇(t)=2et(et-t-1)。

因为et＞t+1,所以g＇(t)＞0,故g(t)单调递增,g(t)＞g(0)=0,命题得证。

四、商的代换,变量化一

例4(2022届皖西七校联考)已知函数f(x)=2lnx-ax2-bx(a,b∈R),g(x)=-lnx。

(1)当a=-2时,f(x)与g(x)在定义域上的单调性相反,求b的取值范围;

(2)设x1,x2是函数f(x)的两个零点,且x1＜x2,求证:＜a(x1+x2)+b。

解析:(1)因为a=-2,所以f(x)=2lnx+2x2-bx,由题意可知,f(x)与g(x)的定义域均为(0,+∞)。

又当a=-2时,f(x)与g(x)在定义域上的单调性相反,所以f(x)=2lnx+2x2-bx在(0,+∞)上单调递增,所以f＇(x)=+4x-b≥0对x∈(0,+∞)恒成立,即b≤+4x对x∈(0,+∞)恒成立,所以只需。

总之,证明或求解双变量函数或不等式的基本思想是将二元函数或不等式转化为一元函数或不等式,可以合理利用双变量之间的关系直接代入消元,也可以分散双变量后直接构造函数,还可以变换不等式使两个变元成为一个整体即重组双变量后换元成单变量的函数,掌握这些常用的方法,则这类函数问题就能迎刃而解。