基于改进BP神经网络探究航班与航空旅客关系

王 欢, 赵 慧, 周正全

(北京市市政工程设计研究总院有限公司, 北京 100082)

随着我国民航业的快速发展，机场的规模和业务量日益扩大，如何在海量航空运输数据的基础上，定量研究航班数量和航空旅客数量的关系，对于保障航班计划的合理制订和机场的高效运行，具有重要的意义. 在以往传统研究中，由于数据体量有限、科学技术落后，对航班数量和航空旅客定量关系的研究相对较少，研究精度相对较低. 现阶段随着科学技术的快速发展，大数据理念和人工智能算法的出现为学术研究和应用实践的开展提供了便利和指引.

基于北京市市政工程设计研究总院有限公司“服务于机场陆侧典型交通设施设计的多源数据挖掘分析”研究报告数据，本文以2017年首都国际机场10月份进港航班和航空旅客数据为例，使用传统的数据拟合方法，如线性拟合、多项式拟合、对数拟合和幂函数拟合等，定量研究二者之间的关系，部分拟合结果如图1所示.

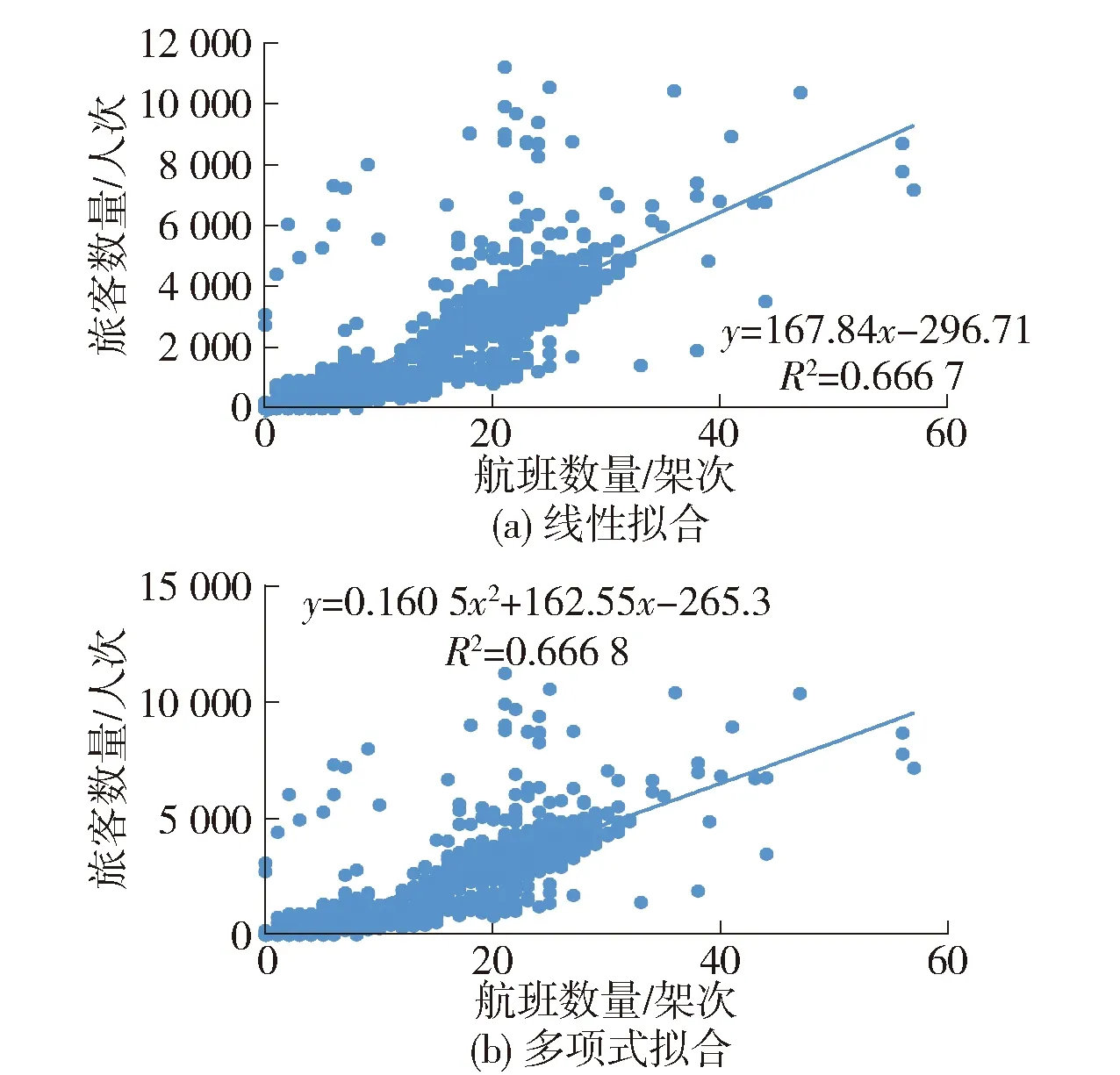
图1 传统拟合结果

从图1中可看出，传统拟合方法的R2在0.7以下，说明拟合效果相对较差. 理想条件下航班数量和航空旅客数量成正相关的关系，但是受票价、满载率、天气等各种因素的影响，传统的数据拟合方法难以准确反映二者之间的关系. 因此，基于海量的航空数据，需要研究一种更为智能的方法，以探究航班数量和航空旅客数量之间的定量关系.

1 改进BP神经网络及其参数选取

1.1 算法

神经网络算法(Back Propagation，BP)是一种广泛应用的人工智能算法. 其基本思想是输入学习样本，使用反向传播算法对网络的权值和偏差进行反复的调整训练，从而使输出向量与期望向量尽可能地接近，当网络输出层的误差平方和小于指定的误差或达到指定训练次数时训练完成，保存网络的权值和偏差[1-3]. BP神经网络算法在理论上可逼近任意函数，基本的结构由非线性变化单元组成，具有很强的非线性映射能力. 但是网络的层数、各层之间的传递函数、网络的训练函数、隐含层神经元的个数和算法运行次数等均会对算法的运行结果产生不同的影响[4].

1.2 参数选取

1.2.1 神经网络层数

BP神经网络的拓扑结构包括输入层、隐含层和输出层. 其中，隐含层可设置多层，网络的复杂程度与隐含层的层数成正相关关系. 研究表明，在闭区间内，单隐层的BP神经网络可用来逼近任何一个连续的函数[5]，因此，本文设置隐含层的层数为1层.

1.2.2 传递函数

BP神经网络的输入层至隐含层、隐含层至输出层之间需要确定两个传递函数. 根据网络输出值的正负，Sigmoid 函数可分为Logsig函数和Tansig函数[6]，其中Logsig函数的输出值在0～1之间，Tansig函数的输出值在-1～1之间，考虑到航班数量和航空旅客数量均为正数，本文选用Logsig函数作为输入层至隐含层的传递函数. 同时，为了更直观地表示航班和航空旅客之间的关系，设置隐含层至输出层之间的传递函数为Purelin线性函数. 输入层至隐含层的传递函数Logsig函数的表达式，见式(1)：

(1)

1.2.3 训练函数

BP神经网络算法的核心步骤是网络的训练，不同的训练函数会导致算法的搜索方式、迭代次数、存储空间和收敛速度有所不同. 常见的训练方法包括最速梯度下降法、有动量的梯度下降法、弹性BP算法、贝叶斯归一法和Levenberg-Marquardt算法等[7-8]. 其中Levenberg-Marquardt算法的应用最为广泛，训练结果比较理想. 因此，本文选用Levenberg-Marquardt算法即Trainlm函数作为BP神经网络算法的训练函数.

1.2.4 隐含层神经元个数

隐含层神经元的个数会影响网络的复杂程度和运算结果，神经元的个数太少，会导致网络不能准确反映输入层和输出层之间的关系；神经元的个数太多，会导致网络的复杂度增加，加大计算难度. 通常采取实验法从较少神经元个数开始训练，依次增加神经元的个数，对比计算结果选择最佳的神经元个数. 依据式(2)[9]来对隐含层神经元的个数进行初始化：

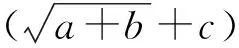
(2)

式中：a和b分别表示输入层和输出层的神经元个数；c为[1,10]之间的随机整数；n为隐含层的神经元个数.

在BP神经网络相关参数确定的前提下，由于训练过程具有一定的随机性，算法每次的运行结果会稍有差异. 本文将90%的数据作为实验数据，搜寻并搭建合适的神经网络；将剩下的10%的数据作为验证数据，测试已构建网络的合理性.

为了保证神经网络算法具有良好的执行效果，在选择最佳隐含层神经元个数时，在同一神经元个数下，多次运行神经网络算法，并计算验证数据集的输出值和目标值的拟合系数以及拟合系数的均值. 拟合系数越接近1，表示输出值越接近于目标值，神经网络的学习效果越好；拟合系数的均值越大，表示对应隐含层神经元的个数越优.

本文定义拟合系数的计算见式(3)：

(3)

隐含层最佳神经元个数的求解步骤如下：

步骤1设定每种神经元个数下算法运行次数为I,设置隐含层神经元个数调整的范围为[N1,N2]，令n=N1.

步骤1.1 输入航班数据和航空客流数据，建立BP神经网络，记录算法运行次数，令i=1；

步骤1.2 运行BP神经网络算法，记录输出值和目标值之间的拟合系数Ri；

步骤1.3 增加算法运行次数，令i=i+1，如果i≤I，返回步骤1.2，否则，执行步骤1.4；

步骤2增加隐含层神经元的个数，令n=n+1，如果n≤N2，返回步骤1.1，否则，执行步骤3.

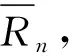
本文以2017年首都国际机场3月、6月和10月份的进港航班和航空旅客数据为例进行仿真实验. 以进港航班数量为输入层数据，以进港航空旅客数量为输出层数据，将进港航班数据和进港航空旅客数据输入BP神经网络算法，遍历隐含层神经元个数，多次运行BP神经网络算法，搜寻隐含层最佳神经元个数. 1个进港航班数据对应1个进港航空旅客数据，因此，输入层和输出层神经元的个数均为1个，隐含层神经元的个数在[3,13]之间依次取值，同一神经元个数下运行BP神经网络算法100次，根据上述隐含层最佳神经元个数求解步骤，计算每种神经元个数下输出值和目标值的拟合系数均值，计算结果如图2所示.

图2 隐含层最佳神经元个数实验结果

从图2中可看出，验证数据集的输出值和目标值的拟合系数均值均在0.78以上，随着隐含层神经元数的增加，拟合系数的均值呈现逐渐增大的趋势，当隐含层神经元数达到10个时，验证数据集的输出值和目标值的拟合系数均值最大，说明此时通过BP神经网络算法训练得到的结果精度较高. 此后，随隐含层神经元个数的增加，拟合系数均值呈现下降趋势，说明并非隐含层神经元的个数越多，神经网络的学习效果越好. 因此，针对本文首都国际机场的航空案例，设定隐含层的最佳神经元个数为10个.

1.2.5 算法停止条件

BP神经网络算法是一种智能的学习算法，该算法的停止条件可设多个，只要满足其中1个，算法就会停止学习. 本文设置3个停止条件，分别是迭代次数、学习目标和验证次数. BP神经网络算法的参数设置如表1所示.

表1 BP神经网络参数设置

BP神经网络的拓扑结构如图3所示. 从图3中可看出，整个网络由3层组成，分别为输入层、单隐含层和输出层. 输入层和输出层神经元个数均为1个，隐含层神经元个数设置为10个，输入层和隐含层之间通过Logsig函数进行连接，隐含层和输出层之间通过Purelin线性函数进行连接.

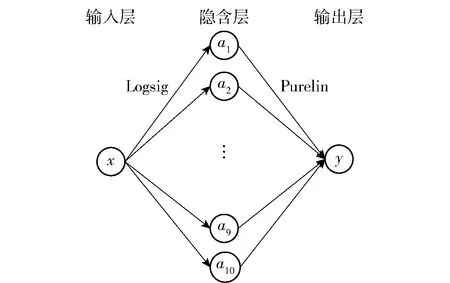
图3 BP神经网络拓扑结构

BP神经网络的网络结构表达式为见式(4)：

(4)

式中：wi为输入层至隐含层第i个神经元的连接权值；bi为输入层至隐含层第i个神经元的连接阈值；wi为隐含层第i个神经元至输出层的连接权值；B为隐含层至输出层的连接阈值.

2 数据处理与仿真实验

使用MATLAB 2014a编写BP神经网络程序代码[10-11]，基于首都国际机场的进港航班和航空旅客数据进行仿真实验.

2.1 数据预处理

本文以2017年首都国际机场3月、6月和10月份的进港航班和航空旅客数据；统计每半小时的进港航班数量和航空旅客数量，研究进港航班数量和航空旅客数量的定量关系. 由于数据统计过程中可能会存在一定的误差，我们对原始数据进行预处理，剔除或矫正异常数据，补全缺失数据，减少数据误差对BP神经网络算法仿真结果的影响.

2.2 仿真实验

本文将航班数据和同一时间的航空旅客数据一一对应，每个航班数据和航空数据组成一组. 将预处理后的数据进行随机排序，消除邻近数据的相似性对结果的影响. 随机将其中90%的数据作为BP神经网络的实验数据，剩下的10%的数据作为仿真实验的验证数据，测试神经网络的学习效果.

我们将实验数据输入到BP神经网络算法中，MATLAB内嵌的BP神经网络工具箱会自动将实验数据分为3部分，分别是Training Set、Validation Set和Test Set. 为了避免BP神经网络算法陷入过度学习状态，出现过拟合现象，在算法使用Training Set进行训练的同时，系统会自动将Validation Set输入训练后的神经网络，计算输出值和目标值的误差，当该误差连续多次不下降或上升，超过系统预先设定的验证次数时，神经网络算法就认为Training Set的训练结果已经达到最优值，此时就会停止训练. BP神经网络算法的收敛过程如图4所示，从图4中可看出，算法执行次数为18次，在第12次学习时算法收敛，此时的MSE为390 800.697 4，未达到学习目标，但是避免了过拟合现象出现.

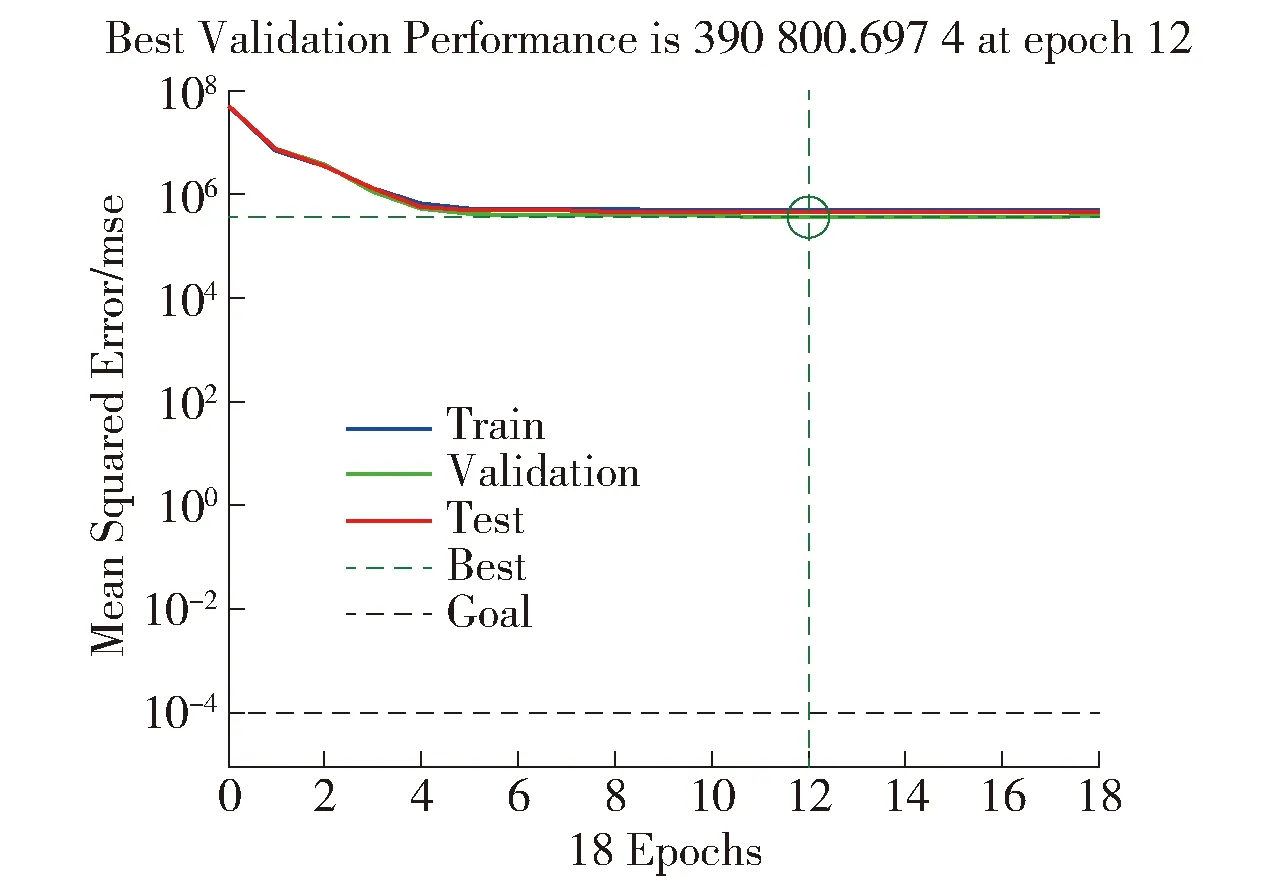
图4 BP神经网络收敛过程

BP神经网络的学习结果如图5所示，图中4个小图分别显示了training set、validation set、test set和全部数据的回归结果，即输出值和目标值之间的拟合程度. 从图5中可看出，大部分数据均集中在对角线上，部分数据离散在对角线附近，拟合结果均在0.85以上，说明拟合效果相对较好.

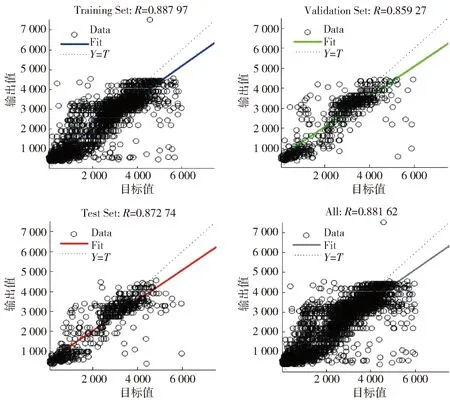
图5 BP神经网络学习结果

基于实验数据训练好的神经网络，我们将剩下的10%的验证数据输入到网络中，任取其中50组数据，输出值和目标值的对比结果如图6所示. 从图6中可看出，输出值和目标值曲线的趋势一致，基本吻合，说明验证数据的目标值和基于训练好的网络计算出的输出值基本一致，再次验证了BP神经网络算法训练结果的准确性.

图6 验证数据集输出值和目标值的对比结果

基于BP神经网络算法，以进港航班数据为输入层，以进港航空旅客数据为输出层，构建得到了训练好的神经网络，网络结构的相关参数如表2所示，根据式(4)可给出相应网络结构的表达式. 基于本文输入的首都国际机场进港航班和航空旅客数据，求得隐含层最佳神经元数为10个，则对应输入层至隐含层神经元的连接权值、输入层至隐含层神经元的连接阈值、隐含层至输出层神经元的连接权值均为10个. 隐含层至输出层之间的传递函数为线性函数，故隐含层至输出层的连接阈值为1个. 网络参数的计算值各不相同，相差较大.

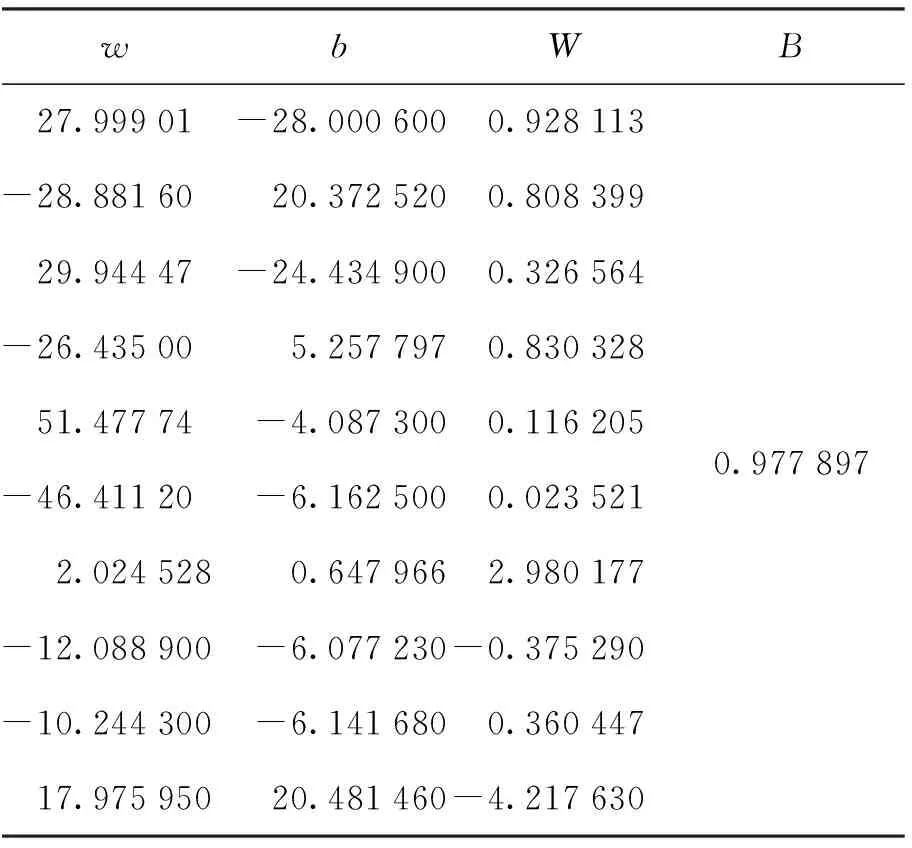
表2 进港航班与航空旅客的网络参数

基于构建好的神经网络和输出的网络结构表达式，在已知首都国际机场航班数据的条件下，可计算得到对应的航空旅客数据. 基于海量的历史数据和人工智能算法，计算出航班和航空客流之间的定量关系表达式，并应用于未来航空客流预测领域，相比传统的数据拟合方法，计算结果更加可靠.

3 结束语

根据实际应用需要，本文对传统BP神经网络算法的参数选取进行了改进，提出以拟合系数均值作为隐含层最佳神经元数优劣评判的定量依据，降低了算法运行结果的不确定性，一定程度上提高了运行结果的可靠性. 相比传统研究方法，本文提出的基于改进BP神经网络算法探究航班和航空旅客定量关系的方法更加高效和准确. 根据不同机场的运营数据，可计算不同机场航班和航空旅客的定量关系，为航空公司航班计划的制订以及航站楼服务设施的建设和改善提供参考依据.

但是，受不同机场航班计划、客流规模、特殊天气等因素的影响，航班和航空旅客定量关系计算结果的准确程度有所差异. 如何统筹考虑机场规模、航班延误等因素，下一步研究的重点是进一步提高航班和航空旅客定量拟合的准确度.