基于改进HOG特征与LPP算法的木材缺陷识别

彭 骞， 张 华， 任万春， 刘 城

(1.西南科技大学 信息工程学院，四川 绵阳 621010； 2.特殊环境机器人技术四川重点实验室，四川 绵阳 621010)

0 引 言

木材在我国建筑、装饰、家具等多个产业中都扮演着非常重要的角色[1]。木材受其自身生长环境、木工机械磨损、工艺条件等因素影响，导致木材表面容易出现各种缺陷。这些缺陷对产品的外观和性能有很大的影响，因此对木材缺陷的检测至关重要。

目前，国内外学者提出了多种木材缺陷的识别方法：三维图像重建的木材缺陷识别[2]、基于多特征融合的木材缺陷研究[3]、超声波与小波变换[4]、阶统计量滤波等，上述方法都能有效地对木材缺陷进行识别。徐梓敬等人[5]利用遗传算法(genetic algorithm,GA)对SVM进行权值和阈值的优化，实现对木材内部缺陷无损识别。熊伟俊等人[6]提出范数算法与局部二值模式(local binary patterns,LBP)特征矩阵对木材缺陷进行识别。Li S等人[7]结合了LBP特征和局部二元差分激励模式完成了对木材缺陷分类。在降维算法方面，有研究学者采用主成分分析(principal components analysis,PCA)法[8]、线性判别分析(linear discriminant analysis,LDA)[9]方法对特征进行降维。陈小芳等人[10]提出流形降维方法能够用于非线性降维，但其本质是保持数据间的局部关系将高维的数据降到低维空间，未能有效处理新样本产生样本外问题。针对这个问题，研究学者提出了局部保持投影(locality preserving projection,LPP)算法，但传统的LPP算法只考虑局部流形特征而忽略全局结构特征。邓士杰等人[11]提出结合PCA和LPP的算法以充分描述样本的全局和局部特性，但LPP算法缺少样本类别信息，影响监督样本降维算法性能。

综上所述，这些方法都具有较高的识别率，但实际的木材缺陷识别过程，易受到噪声干扰。本文通过改进HOG特征与LPP算法来提高木材缺陷的识别率。

1 算法原理

1.1 HOG特征及其改进

HOG特征是由Dalal N和Triggs B[12]提出的一种用于图像处理与目标检测的特征描述子。传统HOG特征的计算是采用[-1,0, 1]和[1,0,-1]T梯度算子进行卷积运算，计算各个中心像素点的水平方向的梯度与垂直方向的梯度，计算公式如下

(1)

式中Gh(x,y)和Gv(x,y)分别为水平和垂直方向的梯度，f(x,y)为像素点的(x,y)灰度值，计算各像素点的梯度幅值G(x,y)和方向θ(x,y)，其计算公式如下

(2)

(3)

但传统的HOG特征只对各像素点水平及垂直方向的梯度幅值与梯度方向进行提取，忽略了周围其他邻域像素值的影响，可能会导致局部信息的丢失；同时，传统HOG特征的子窗口尺寸过小，会弱化平滑效果致使降噪效果差，从而降低最终识别率。

针对传统HOG特征存在的不足，对图像进行多尺度的HOG特征提取。不同尺度的HOG特征示意图如图1所示。其中，R表示尺度半径，P表示邻域像素点数量。从图1中可以看出，随着HOG特征的子窗口尺度半径与邻域像素点数量增加，提高了与周围其他邻域像素的联系，弥补细节丢失造成的对图像描述的不足。

图1 多尺度HOG特征示意

但多尺度的HOG特征不能直接进行梯度计算，从图2中可以看出，梯度对应的邻域像素点位置并没有完全对应具体的像素点，因此，在对图像提取各个方向梯度之前，需要对每一个像素点对应邻域像素点求解其亚像素值。

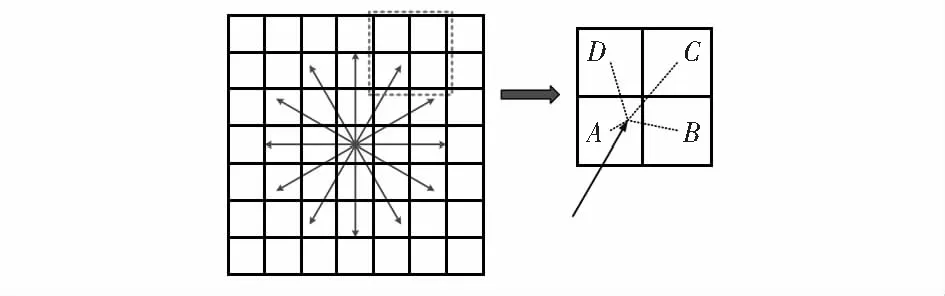
图2 多尺度HOG特征的亚像素值示意

如图3所示，其中Q点表示亚像素点的位置，而A,B,C,D点表示该亚像素点周围的领域像素点。采用距离进行计算：通过求解Q点分别到A,B,C,D点的距离，并将其距离的倒数求和分别计算各自的权重，最终Q点的亚像素值为各点像素值乘以各自权重之和，其计算公式如下

(4)

(5)

式中A(x,y)，B(x,y),C(x,y),D(x,y)点分别为各自的像素值，Q(x,y)为Q点对应的亚像素值，Total为总的权重。

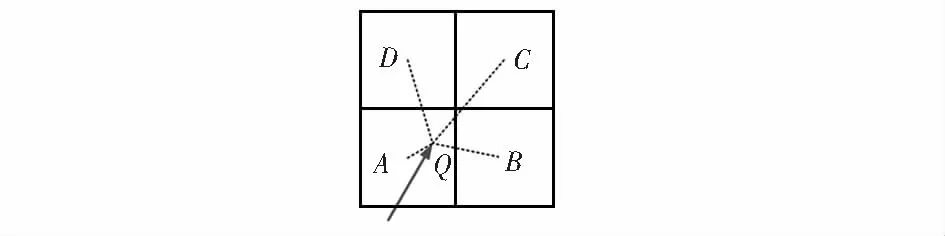
图3 亚像素值计算

多尺度下的HOG特征存在多个不同方向的梯度，因此,需要斜方向的梯度进行正交分解，同一分解水平与垂直方向的梯度,如图4所示。

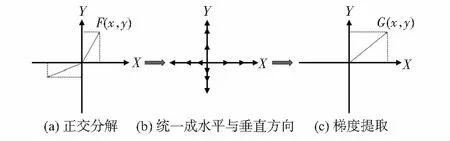
图4 多尺度HOG梯度提取

从图4(a)中可以看出，可以将任意方向的梯度分解成水平与垂直方向，其计算公式如下

(6)

式中F(x,y)任意方向的亚像素值，其中,Fx(x,y),Fy(x,y)分别为F(x,y)在水平与垂直方向上的分解，δ为F(x,y)与x轴水平方向的夹角。

从图4(b)中可以看出:将任意方向的梯度分解水平与垂直方向，极大程度简化了梯度的计算复杂程度。最终通过对反方向的水平与垂直的梯度进行相互化简与低效，如图4(c)所示，最终的梯度计算公式如下

(7)

(8)

式中Gx(x,y)与Gy(x,y)分别为最终分解合成后的水平与垂直方向的梯度，G′(x,y)与θ′(x,y)分别为其改进的梯度幅值与梯度方向。

1.2 LPP算法及其改进

LPP算法是He X F[13]提出的一种流形降维方法。LPP算法通过对样本集进行投影，得到相应的低维子空间，其本质是对拉普拉斯特征映射的线性逼近。但传统的LPP算法只考虑局部流形特征的缺陷，并且缺少监督信息降低算法性能。本文采用陈小芳等人提出的LPP改进算法[10]，通过融合PCA 算法以增强全局信息处理能力，并使用样本标签信息重构加权矩阵改进LPP算法的目标函数。

PCA算法的目的是找到一个投影矩阵W使得低维空间中的数据样本具有最大的方差，其目标函数如下

=maxWTCW

(9)

PCA通过在投影空间保留数据集的大部分方差信息实现线性空间投影，保留了样本的全局结构特征，与LPP算法融合后，弥补PCA算法对局部结构信息描述缺乏的不足。但LPP算法作为非监督降维方法，缺少监督信息影响算法性能，因此,本文中使用类别信息重构加权矩阵以改善算法性能，LPP算法的目标函数如下

=minWTXLXTW

(10)

其中，权重矩阵Sij为xi和xj之间的近邻关系。

传统的LPP首先通过 FCM 聚类构造一点加权邻接图G，其中顶点表示高维数据，边代表相邻关系，如果数据xi和xj具有邻近关系，则G中顶点i和j边连接，与xi距离最近的k个点组成样本集Ni。本文通过判断xi和xj是否属于同一类别赋予不同的权重值,代替传统算法中的权重值来改进原算法，属于和不属于xi的样本分别构成样本集Li,Mi。改进的权重矩阵Sij如下

(11)

其中，当Sij既不属于Li，也不属于Mi时，Sij=0。

从式子中可以看出，当xi与xj属于同一类别时，权重值自适应增加，当不属于同一类别时，权重值会有所减低，从而实现监督信息融入LPP算法。

融合PCA的全局目标函数和LPP算法的局部目标函数，得到本文降维算法的目标函数如下

(12)

2 算法流程

1)读取大小为400×400的训练图像，设置分块大小为50×50，将图像分为8×8=64个块，计算LBP特征的等价模式，得到每个块的59维直方图特征，并将每个块的特征向量相连起来得到改进的64×59=3 776维LBP特征向量。2)设置分块大小为40×40，将图像分为10×10=100个块，提取图像的100×16=1 600维HOG特征向量。并将多尺度HOG特征与LBP特征进行融合，得到5 376维融合特征。3)通过改进LPP算法将5376高维融合特征降维得到100维特征。4)将上述降维后的特征放入SVM支持向量机中进行训练识别。本文的算法流程图如图5所示。

图5 本文算法流程

3 实验结果与分析

3.1 实验条件与环境搭建

实验硬件环境为Intel®CoreTMi7—8700处理器、16 GB内存，软件环境为Windows10系统、Visual Studio 2015软件。采用型号为MER—130—30UM-L的工业数字摄像机对木材缺陷进行图像采集，并且采集的数据集中包含4类木材缺陷，分别为虫眼、活节、死节、裂纹，如图6，每类有300张图片。随机选取240张图像训练，60张图像用于测试，并实验10次，实验结果取平均。为了说明算法的抗噪性能，在测试集中加入不同信噪比的高斯噪声。

图6 本文缺陷数据集的示例图像

3.2 特征尺度选取

选择加入高斯噪声的信噪比为60 dB的测试集进行测试，选取不同尺度的改进HOG特征进行实验对比，其实验结果如表1所示。可以看出:当尺度半径R=2.5并且并采用欧氏距离法具有最高识别率91.25 %。因此，本文采用选取HOG特征尺度半径R=2.5。

表1 不同尺度HOG特征的总体识别率

3.3 多尺度HOG特征的抗噪性能分析

在不同高斯噪声下,分别采用多种不同特征进行缺陷识别，实验对比结果如表2所示。本文改进HOG+LBP特征相比LBP特征，识别率分别提高了13.56 %,20.42 %,21.54 %,11.25 %,7.72 %；相较于HOG+LBP特征，增加了邻域像素的联系，弥补了由于局部信息丢失而导致的对图像描述不全面的缺点，识别率分别提高了3.46 %,5.83 %,7.57 %,2.7 %,6.26 %；相较于传统的LBP特征，识别率分别提高了5.88 %,12.92 %,17.58 %,9.25 %,6.88 %。

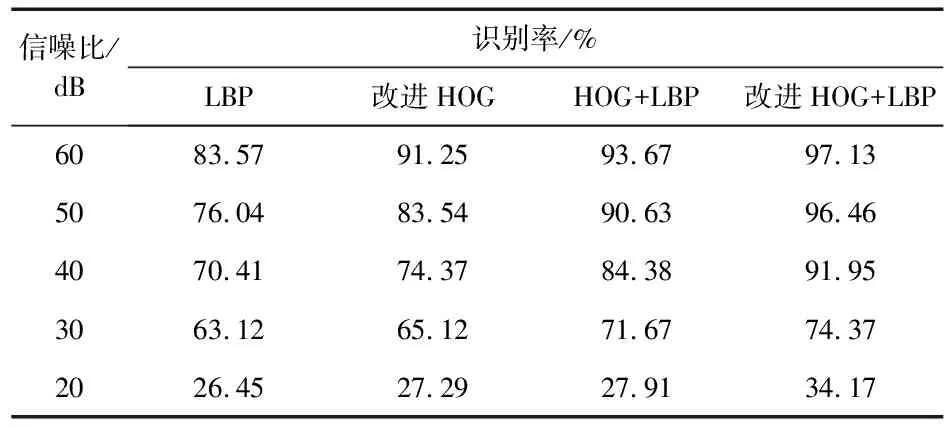
表2 不同高斯噪声下采用不同特征的总体识别率对比

3.4 改进LPP算法的抗噪性能分析

本文采用不同的降维算法进行了比较实验，选择信噪比为60 dB的测试集进行测试，改进HOG+LBP+改进LPP、改进HOG+LBP+LPP、改进HOG+LBP+PCA、改进HOG+LBP+LDA的识别率分别为97.13 %,94.71 %,91.45 %,94.21 %。可以看出，使用改进的LPP降维算法最优最高识别率97.13 %，这是由于改进后的LPP算法，增强全局信息处理能力，同时使用样本标签信息改进LPP目标函数中的加权矩阵，弥补了缺少监督信息影响算法性能。

4 结束语

本文通过对HOG特征与LPP算法进行了改进，弥补了局部信息丢失而导致对图像描述不全面的缺点，提高了对噪声的鲁棒性。在信噪比为60 dB的环境下，识别率可以达到97.13 %。结合对比实验结果分析，本文算法识别精度均高于其他几种缺陷识别算法，能有效地识别木材缺陷。但本文算法只适用于信噪比大于等于40 dB的条件下，在后续的研究中，可以增加样本数量、使用增量学习方法，进一步提升算法抗噪性能。