基于快递员行为的城市末端共同配送定价研究

孔继利，陈璨，刘晓平

(北京邮电大学 现代邮政学院，北京 100876)

一、引 言

当前，快递行业正处于高速发展阶段，是中国经济增长和区域发展的新动力[1]。快递服务质量逐渐成为提升人民生活品质的重要指标。随着消费者对物流配送极致需求的日益增强，快递企业的配送压力急剧增加[2]，导致快件滞留时间长、行业内价格战激烈[3]、配送服务质量下降等。为了有效解决快递行业面临的上述问题，国家鼓励企业构建共同配送联盟，推动共同配送模式的应用。例如，2020年，国家邮政局发布的《邮政强国建设行动纲要》明确要“鼓励寄递企业开展共同配送”。与此同时，快递企业积极响应国家号召，扎实推进共同配送工作的落实。例如，“三通一达”的部分末端快递网点开始自发合作，整合配送基础设施与人力资源，实施共同配送。

国内外有不少文献聚焦共同配送模式的研究，本文重点关注共同配送背景下的定价问题。在定价研究方面，Yan等[4]以两级生鲜农产品供应链为对象，研究基于两阶段价格、批发价格和期权契约的供应链最优订货和协调问题；Farshbaf-Geranmayeh等[5]考虑季节因素和广告影响，研究分散定价和集中定价问题，确定销售季节内折扣的次数和每次折扣的力度；Gupta等[6]研究供应中断风险下，供应中断时间对产品定价决策的影响，并设计了降低中断风险的订购策略。定价问题虽然在供应链、物流领域的研究较为成熟，但在共同配送领域研究相对较少，主要集中于定价决策与生鲜电商合作[7-8]、农产品用户需求偏好[9]、铁路协同联运[10]等方向。关于快递员对配送影响方面的研究，已有文献考虑的是快递员的评价考核[11]、服务态度[12]、仅提供自提服务[13]、自提与上门服务的矛盾[14]等对末端配送的影响。

在充分借鉴上述文献研究成果的基础上，基于收益分配和成本分担的基础理论，本文引入快递员的工资水平、快递员的配送选择行为、共配中心的价格敏感程度等影响因素，使用Stackelberg博弈理论构建多阶段共同配送模型，分析末端共同配送全过程中各参与方对定价博弈的影响，以期为城市末端共同配送联盟的构建和稳定发展提供理论指导。

二、基于快递员行为的城市末端共同配送定价

(一)问题描述

本文以快递企业、共配中心、承包区、快递员、快递柜(驿站)经营企业为城市末端共同配送不同阶段的参与方，研究快递员行为对末端配送全过程服务定价的影响。假设n个快递企业在某一配送区域内有配送需求。在非共配模式下，由各快递企业分别使用独立的配送渠道进行配送；在共配模式下，由统一的共配中心为多家快递企业提供配送服务，快递企业需支付共配中心一定的派费。之后，共配中心按区域配送需求合理划分承包区，将快件分配给承包区，并支付承包区一定的派费。再由承包区将快件分配至快递员，支付快递员一定的派费。快递员可自由选择直接配送至用户，或者支付一定的服务费使用快递柜或驿站等进行末端配送。具体应用场景如图1所示。

图1 共同配送的应用场景

(二)模型假设

目前，常用的定价模型主要有Stackelberg博弈[15]、收益共享契约[16]、集中决策[17]等。在共同配送场景中，快递企业可以选择使用共配中心或不参与共配，共配中心规划承包区范围，承包区雇佣快递员进行配送服务，快递柜和驿站的暂存快件量有限，博弈各方存在对立的竞争关系，且博弈地位不平等，故选择Stackelberg博弈理论构建定价模型。本文以李洋等[15]7对三级供应链利益分配机制和定价策略的研究为基础，分析快递企业与共配中心、共配中心与承包区、承包区与快递员、快递员与快递柜(驿站)经营企业之间的定价博弈策略，构建Stackelberg定价博弈模型，提出如下假设：

(1)非共配模式下，快递企业i需支付配送中心单票派费pci完成快件的末端配送服务。

(2)共配模式下，在配送区域内，由共配中心为n家快递企业提供末端配送服务，快递企业i需支付共配中心单票派费p1i元。

(3)共配中心的单票快件成本为cd元，共配中心需支付承包区单票派费p2元。

(4)m个承包区雇佣快递员进行末端快件配送服务，承包区的单票快件成本为cw元，承包区需支付快递员单票派费p3元。

(5)g个快递员自行选择直接配送方式，直接派送的快件比例k1，投放驿站的快件比例k2，投放快递柜的快件比例k3。其中，k1+k2+k3=1。

(6)快递企业i的派件量D1i与快递企业i的历史月派件量di、支付给共配中心的单票派费p1i、快递员在某区域行业平均月工资水平s、共配中心的配送信用rd、共配中心的配送效率ed等因素有关，且呈线性关系。当快递企业需支付的单票派费、快递员的月均工资水平提高时，快递企业的派件量减少；当共配中心的配送效率、配送信用提高时，快递企业的派件量增加。快递企业i的派件量函数如下所示：

D1i=ρidi-θ1ip1i-θ2is+θ3ird+θ4ied

(1)

其中，历史月派件量di对派件量的影响因子为ρi，单票派费p1i对派件量的影响因子为θ1i，行业平均月工资水平s对派件量的影响因子为θ2i，共配中心的配送信用rd对派件量的影响因子为θ3i，共配中心的配送效率ed对派件量的影响因子为θ4i。

(7)共同配送定价博弈各参与方的竞争地位不对等。在快递企业与共配中心的博弈定价过程中，快递企业处于主导地位；在共配中心与承包区的博弈定价过程中，共配中心处于主导地位；在承包区与快递员的博弈定价过程中，承包区处于主导地位；在快递员与快递柜(驿站)经营企业的博弈定价过程中，快递柜、驿站经营企业处于主导地位。

(8)不考虑顾客偏好、退货、二次配送、商品损坏、政府政策支持等情况。

(三)符号定义

基于上文对共同配送定价问题的描述和假设，对模型所需变量和参数符号进行定义，如表1所示。

表1 变量及参数符号定义

(四)快递企业与共配中心的定价博弈模型

在快递企业和共配中心进行博弈的过程中，以参与共配前后快递企业支付配送中心、共配中心派费的差值作为快递企业的收益，故需保证参与共同配送后快递企业支付的单票派费低于共同配送前的单票派费。在非共配模式下，各快递企业分别与已有的配送中心合作，配送中心提供配送服务，快递企业支付配送中心单票派费。在共同配送模式下，由n家快递企业与共配中心单独进行定价博弈，各家快递企业分别支付共配中心不同的单票派费，互不影响。在博弈过程中，假设快递企业有选择共配中心的主动权，处于博弈优势地位。基于以上假设，构建快递企业与共配中心的Stackelberg定价博弈模型。

快递企业的收益是非共配模式下的派费与共配模式下派费的差值，收益函数为：

Π1i=(pci-p1i)D1i=(pci-p1i)(ρidi-θ1ip1i-θ2is+θ3ird+θ4ied)

(2)

共配中心的收益是快递企业支付共配中心的派费减去共配中心的运营成本及向承包区支付的派费，共配中心需完成所有快件的配送服务，收益函数如下所示：

Π2i=(p1i-cd-p2i)D1i=(p1i-cd-p2i)(ρidi-θ1ip1i-θ2is+θ3ird+θ4ied)

(3)

此时，化简快递企业的收益函数，令Ki=ρidi-θ2is+θ3ird+θ4ied，可得D1i=Ki-θ1ip1i，那么Π1i=(pci-p1i)(Ki-θ1ip1i)。再基于一阶最优性原则分析单票派费对快递企业收益函数的影响，如下所示：

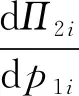
(4)

(5)

由式(5)可知，快递企业i收益函数的二阶导数始终大于0，故Π1i是一个凹函数，在不确定函数定义域的情况下仅存在最小值，无法求得最大收益。

基于此，研究共配中心的收益函数。化简共配中心的收益函数，可得Π2i=(p1i-cd-p2i)(Ki-θ1ip1i)，分析单票派费对共配中心收益函数的影响，如下所示：

(6)

(7)

(8)

此时，以式(8)与快递企业非共配模式下的单票派费比较，商议最终的单票派费。若式(8)的单票派费小于非共配模式下快递企业i的单票派费，即直接为最终的单票派费；若式(8)的单票派费大于非共配模式下快递企业i的单票派费，则需要进一步调整单票派费至双方均可接受的范围(即对于快递企业i而言低于非共配模式下的单票派费，对于共配中心而言高于其总成本)。

(五)共配中心与承包区的定价博弈模型

在共配中心与承包区博弈时，共配中心为承包区统一定价。在实际应用中，不同承包区可能存在不同的派费，但在模型构建时忽略这种差异，从而构建一个各承包区都能作为定价依据的合理模型。在构建定价博弈模型时，承包区之间不存在竞争关系，承包区负责的配送区域已划定。同时，考虑共配中心给承包区的派费高于承包区的配送成本，以此保证承包区的正常盈利。共配中心划分承包区的服务范围，因此，共配中心处于博弈优势地位。基于以上假设，构建共配中心与承包区的Stackelberg定价博弈模型。

共配中心的收益函数在上文中已详细分析，此处仅分析承包区的收益函数。

承包区的收益是共配中心支付承包区的派费减去承包区的运营成本及承包区支付快递员的派费，收益函数如下所示:

Π3i=(p2i-cw-p3i)D1i

(9)

基于式(8)的分析过程，将式(8)代入式(9)，可以得到共配中心收益最佳时承包区的收益函数，即:

(10)

之后，分析单票派费对承包区收益函数的影响，如下所示:

(11)

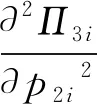
(12)

(13)

(六)承包区与快递员的定价博弈模型

在承包区与快递员博弈时，承包区为快递员统一定价。在实际应用中，不同快递员配送的快件数量不同，但承包区支付快递员的单件派费是相同的，在模型构建时忽略快递员派件效率的差异，以所有快递员作为一个整体构建模型，仅假设快递员群体每月需完成承包区划分的配送需求，从而构建一个各承包区都能作为定价依据的合理模型。在构建定价博弈模型时，考虑承包区支付快递员的派费高于快递员本身的配送成本，从而保证快递员每月所做的派件工作都是正常盈利的。承包区依据自身的配送业务量雇佣快递员，故承包区处于博弈优势地位。基于以上假设，构建承包区与快递员的Stackelberg定价博弈模型。

承包区的收益函数在上文已详细分析，此处仅分析快递员的收益函数。

快递员的收益是承包区支付快递员的派费减去快递员的配送成本。基于此，由于快递员自行选择最终的末端配送方式，单票配送成本应与快递员做出的实际派件方式抉择、快递员与快递柜(驿站)运营企业的博弈结果有关，下文再对快递员单票配送成本的计算进行详细分析。快递员的收益函数如下所示：

Π4i=(p3i-cpi)D1i

(14)

基于式(13)的分析过程，将式(13)代入式(14)，可以得到承包区收益最佳时快递员的收益函数，即：

(15)

之后，分析单票派费对快递员收益函数的影响，如下所示：

(16)

(17)

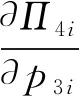
(18)

(七)快递员与快递柜(驿站)经营企业的定价博弈模型

在快递员与快递柜(驿站)经营企业博弈时，快递柜、驿站经营企业分别与快递员定价互不干扰。在实际派件过程中，快递员的配送成本主要由支付快递柜、驿站经营企业的服务费组成，故快递员的单票配送成本是这两项服务费的加权值。在构建定价博弈模型时，考虑快递柜(驿站)经营企业制定的服务费高于其经营成本，从而保证快递柜(驿站)经营企业的持续盈利。快递柜(驿站)经营企业仅提供快件暂存服务，快递员为了完成配送业务量必须使用该服务，故快递柜(驿站)经营企业处于优势地位。基于以上假设，构建快递员和快递柜(驿站)经营企业的Stackelberg定价博弈模型。

1.快递员与快递柜经营企业博弈情形分析

快递柜经营企业的收益是快递员支付快递柜经营企业的服务费减去快递柜经营企业的运营成本，收益函数如下所示：

Π4i=(pri-cr)D1ik2

(19)

基于式(18)的分析过程，将式(18)代入式(19)，可以得到快递员收益最佳时快递柜经营企业的收益函数，即：

(20)

之后，分析单票派费对快递柜经营企业收益函数的影响，如下所示：

(21)

(22)

(23)

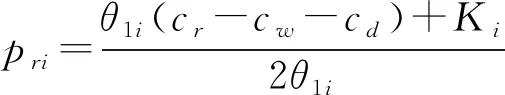
2.快递员与驿站经营企业博弈情形分析

驿站经营企业的收益是快递员支付驿站经营企业的服务费减去驿站经营企业的运营成本，收益函数为：

Π5i=(psi-cs)D1ik3

(24)

基于式(18)的分析过程，将式(18)代入式(24)，可以得到快递员收益最佳时驿站经营企业的收益函数，即：

(25)

之后，分析单票派费对驿站经营企业收益函数的影响，如下所示:

(26)

(27)

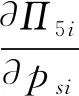
(28)

最后，基于逆向推导法的主要思想，依据上述对快递员与快递柜(驿站)经营企业的定价博弈分析，综合式(23)、式(28)推导快递员的实际配送成本，再结合式(13)分析承包区给快递员的派费，从而推导共配中心和快递企业的定价策略。

由于快递柜和驿站经营企业分析的两种定价博弈模型中考虑的因素不同，采用上述方法计算出的快递员直接配送、投放快递柜及驿站的快件量并不完全等于k1:k2:k3，需依据式(18)、式(22)以及快递员直接配送模式下的成本，定义快递员的实际单票配送成本，合理预估快递员负责的“最后一公里”配送成本。

假设依据快递柜(驿站)经营企业的服务费、快递员投放快递柜(驿站)的比例系数，合理计算快递员的实际配送成本，即:

cpi=prik2+psik3

(29)

由式(18)可得承包区给快递员的单票派费，即:

(30)

将式(30)代入式(13)可得共配中心给承包区的单票派费，即:

(31)

将式(31)代入式(8)可得快递企业给共配中心的单票派费，即:

(32)

(八)定价博弈分析结果综合

基于上文对城市末端共同配送全过程的定价博弈分析，得出n家快递企业均与共配中心博弈后的综合定价结果。其中，快递企业的定价结果为博弈后的直接结果，共配中心、承包区、快递员、快递柜(驿站)经营企业的定价结果为n家快递企业均博弈后的综合结果。

快递企业i支付共配中心的最佳派费为：

(33)

快递企业i给共配中心的派件量为：

(34)

快递企业i的收益为：

(35)

共配中心支付承包区的最佳派费为：

(36)

共配中心的总派件量为：

(37)

共配中心的总收益为：

(38)

承包区支付快递员的最佳派费如下所示：

(39)

承包区的总派件量为：

(40)

承包区的总收益如下所示：

(41)

快递员的配送成本为：

(42)

快递员的总派件量为：

(43)

快递员的总收益为：

(44)

快递柜经营企业的最佳服务费为：

(45)

快递柜经营企业的派件量为：

(46)

快递柜经营企业的收益为：

(47)

驿站经营企业的最佳服务费为：

(48)

驿站经营企业的派件量为：

(49)

驿站经营企业的收益为：

(50)

其中，Ki=ρidi-θ2is+θ3ird+θ4ied。

基于以上综合定价结果可知：本文构建的定价模型，仅在快递企业与共配中心博弈时依据不同快递企业的实际配送需求制定不同定价策略，默认承包区、快递员、快递柜(驿站)经营企业在城市末端配送环节的主要任务是完成所划分区域内的配送需求，且默认划分各区域内的配送需求量相同；快递员在末端配送环节具有自主决策性，其工资水平、末端配送模式的选择都能影响定价决策结果。所以，对快递企业、快递员这两个博弈参与方分别进行详细分析。

1.快递企业分析

快递企业给共配中心的定价结果如式(32)所示，可知单票派费与Ki、θ1i相关。在快递企业的派件量函数(式(1))中，假设行业平均月工资水平、配送中心的配送信用及配送效率均为定值，同时假设这些因素对企业派件量的影响程度也相同。当与派件量相关的各项影响因子(即θ1i，θ2i，θ3i，θ4i，ρi)都相同时，派件量仅与历史派件量呈正相关，即历史派件量越大，预测的实际派件量越大，Ki也越大。此时，快递企业给共配中心的单票派费也就越大。

在这种情况下，派件量越大的快递企业，所需支付的单票派费越高，不符合实际定价规律(在实际定价过程中，共配中心为了实现规模效益，会给派件量更大的快递企业制定更低的单票派费)。因此，在与派件量相关的各项影响因子都相同的情况下，保持θ2i，θ3i，θ4i，ρi不变，通过改变不同快递企业θ1i的大小，调整单票派费至合理的范围内。

进一步分析式(33)，可得：

(51)

其中，α，β，ω，κ为常数项。

由式(51)可知：针对历史派件量di较小的企业，应合理降低θ1i，制定较高的单票派费，得到的定价结果才能符合实际定价规律，有利于共同配送联盟的稳定发展。

2.快递员分析

与快递员相关的定价博弈主要包括快递员派件模式的选择、快递企业的派件量函数等两个部分。

快递员派件模式的选择主要影响快递员的配送成本。在实际末端配送应用中，直接配送上门的模式花费时间最长，但不需快递员付出额外成本；投放快递站的模式花费时间较短且成本较低，但对用户而言，投放快递柜的快件可能由于超时收货而导致用户付费，且快递柜存放的快件量与覆盖范围均有限；投放驿站的模式花费时间较短但成本较高，用户可在驿站工作时间范围内随时取件。

依据快递员的派件模式分析快递员的实际配送成本。由式(42)可知：快递员的配送成本与快递柜(驿站)经营企业的服务费呈正相关；当快递员选择投放驿站的快件量减少或投放驿站的快件量增加时，快递员的配送成本会增加，直接导致其他博弈参与方定价的提高。

快递企业的定价函数和派件量函数如式(33)、式(34)所示，可知：当快递员的配送成本上升时，快递企业的单票派费上升，快件量下降，不利于快递企业和共配中心的长期稳定合作，故需要合理控制快递员的配送成本。

同时，快递员的行业平均月工资水平也会影响快递企业的定价结果，对式(33)进行详细分析，可得：

(52)

其中，α′，β′，ω′和κ′为常数项，且均大于0。

依据式(52)可知：当快递员的行业平均月工资水平较高时，快递企业的单票派费会降低，从而降低快递员派件工作的收入，维持快递员工资水平的稳定，有利于企业的长期发展和共同配送联盟的稳定扩张。

三、算例分析

基于上文对定价博弈模型的分析总结，依据在实际共配场景下收集的数据进行算例分析。

在北京某区域的城市末端共同配送网络中，快递企业给共配中心的单票派费在1.7～2.0元，不同快递企业的派费价格略有浮动，共配中心一天的派件量在30 000件左右，快递员直接送货上门的比例约为40%。基于共同配送的实际运营数据，本文设计合理的算例分析定价博弈模型。

在区域内行业层面，通过调研得到快递员的行业平均月工资水平为0.8万元。

在快递企业层面，快递企业1的历史平均月派件量为24万票，非共配模式下快递企业1的单票派费为2元，历史平均派件量对派件量的影响因子为20，共配模式下单票派费对派件量的影响因子为215，共配模式下行业工资水平对派件量的影响因子为10，共配中心配送信用对派件量的影响因子为0.002，共配中心配送效率对派件量的影响因子为2，其他企业的参数信息见表2。

表2 快递企业的参数信息表

在共配中心层面，共配中心的单票快件成本为0.5元，配送信用为90(假设数值范围为[0,100]，0表示最低信用，100表示最高信用)，配送效率为0.90(假设数值范围为[0,1]，0表示最低效率，1表示最高效率)。

在承包区层面，承包区的单票快件成本为0.2元。

在快递员层面，假设快递员直接配送快件的比例为40%，投放快递柜的比例为50%，投放驿站的比例为10%。

在快递柜及驿站运营企业层面，快递柜的单票运营成本为0.25元，驿站的单票运营成本为0.6元。

将以上数据代入定价博弈模型中，可得如表3所示的定价及收益结果。

表3 共同配送联盟的定价及收益表

基于以上数据计算，分析Stackelberg定价模型的数据结果。首先，在加入共同配送联盟后，各家快递企业的派费明显下降，如图2所示；同时，共配中心、承包区、快递员、快递柜(驿站)经营企业等各参与方均能获得收益。

图2 非共配模式和共配模式下快递企业单票派费对比图

当其他三家快递企业的θ1i与快递企业1的θ1i相同时，即对于所有快递企业而言派件量大小对派费的影响相同，得到的快递企业定价及收益结果如表4所示。

表4 快递企业影响因素均相同时的定价结果及收益表

表3和表4的数据验证了对快递企业派件量影响因子的分析，进一步说明在实际定价分析过程中，本文构建的模型可以制定合理的定价机制，协调快递企业需支付的单票派费至合理区间，从而合理解决城市末端共同配送模式下的定价及收益分配问题。

其次，分析快递员行为对单票派费的影响。先分析快递员派件模式的选择对单票派费的影响。调整快递员选择直接配送、快递柜派送和驿站派送的比例，分析直接派件量较高(k1=0.8，k2=0.1，k3=0.1)、 驿站派件量较高(k1=0.1，k2=0.1，k3=0.8)情形下的快递企业单票派费，可以得到如表5和表6所示的快递企业定价及收益结果。

表5 直接派件量较高时快递企业的定价结果及收益表

表6 驿站派件量较高时快递企业的定价结果及收益表

将表3、表5和表6的计算结果做对比，可验证上文对快递员派件模式的分析。当快递员更多地选择直接配送时，快递员的派件成本降低，导致快递企业的派费降低，从而吸引更多的快递企业使用共配中心；但直接配送比例的提高，会显著影响快递员的派件效率，导致快递员无法完成派件量。当快递员更多地选择高效率、无限制的驿站派件时，快递员的派件成本提高，快递企业需支付的派费也提高，导致共配中心的价格优势降低，规模效益降低，不利于共配联盟的发展。因此，快递员的派件模式制定对共配联盟的稳定发展有重要影响。

再分析快递员的行业平均月工资水平对单票派费的影响。基于表2设定的参数，适度调节快递员的行业平均月工资水平至0.4万元/月和1.2万元/月，可以得到如表7和表8所示的快递企业定价及收益结果。

表7 不同工资水平(0.4万元/月)下快递企业的定价结果及收益表

表8 不同工资水平(1.2万元/月)下快递企业的定价结果及收益表

对比表3、表7和表8的计算结果，可知快递员的行业平均月工资水平越高，快递企业需要支付的派费越低，验证了定价博弈的分析结果。

综上所述，基于对快递企业派件量、快递员的派件模式选择和行业平均月工资水平的分析，能为共同配送联盟定价策略的制定提供理论依据，从而维系联盟的稳定、长远发展。

四、结 论

以共同配送为研究背景，基于快递员行为对快递企业收益的影响，本文构建了4级Stackelberg定价博弈模型，得出如下结论和建议：

(1)构建共同配送联盟的前提是配送成本的降低，联盟应合理规划配送设施设备及资源，综合各参与方能力，最大程度降低配送成本。共同配送联盟的构建，整合了多家快递企业的设施设备、资源和运力，但若参与共配后联盟内部无法合理规划资源，导致快递企业的配送成本上升，共配联盟将无法维持稳定。基于图2的对比分析可知，在本文的定价博弈模型下，快递企业在参与共配联盟后配送成本均有效降低。

(2)定价分析要以实际运营情况为基础，制定参与各方都能接受的、符合发展规律的价格策略，调动企业优化配送流程、提升配送质量的积极性。参与共同配送的各方期望达到的首要目标是收益最大化，但在实际运营过程中，基于市场化的外部环境，定价策略的制定需要衡量多方的收益情况。在对快递企业派件量进行重点分析时，本文结合实际市场“派件量越高、派费越低”的情况，合理调整定价参数。此外，价格敏感程度的提高会导致定价结果的降低，这符合“价格战”激烈时的市场发展情况。

(3)快递员行为对配送质量有重要影响，承包区要制定可操作、标准化的快递员配送指南，提升“门对门”的配送服务质量。在配送过程中，快递员作为快递物流的最后一环，直接与客户对接，影响客户对快递企业服务的整体印象。同时，快递员配送模式的选择，直接影响快件的配送成本，是降低共同配送联盟总成本的重要部分。由承包区雇佣数量合适的快递员并为其分配合理的快件量，由共配中心为承包区和快递员制定标准化配送作业流程，是提升共同配送联盟配送质量的重要手段。

此外，对未来城市末端共同配送服务定价研究做出如下预测：

(1)定制化服务。随着快递服务质量的不断提升和用户需求的变化，快递的时效化、尊享化、特殊化服务成为需求热点。针对不同服务人群，快递企业定制化服务的定价策略制定还有待研究。

(2)智能化手段。结合云计算、区块链、机器学习等人工智能方法，为定价博弈研究提供智能化方向，从而制定符合实际、高效快捷、简单易操作的动态智能定价策略。