一种基于滤波器组设计的多频带组合信号增强方法

陈允锋，刘 超

（1. 海装上海局驻无锡地区军事代表室，江苏无锡 214061；2. 海鹰企业集团有限责任公司，江苏无锡 214000）

0 引 言

信号检测在雷达、声呐和语音等领域中占有重要的地位[1-4]。因此，如何在复杂背景中准确检测感兴趣的信号一直是声呐、雷达和语音等领域中信号处理所关心的研究内容之一。目前，比较经典和常用的信号检测方法有互相关检测法[5]、平方律检波器法[6-7]、能量累积检测法[8-10]等。其中，能量累积检测法由于其复杂度低，被广泛应用。但是该类检测法需要一定的信噪比，在信噪比较低的情况下，对未知信号检测效果较差，需要采取一定的滤波手段对数据进行增强处理，以提高信噪比。

为了对处理数据中期望信号实现增强，提升信号检测效果，研究者提出了一些信号的增强方法，并取得了一定的应用效果，如参数方法、非参数方法以及统计方法[11-16]。在参数方法中主要代表性方法为：梳状滤波器、维纳滤波和卡尔曼滤波方法等[11-12]；非参数方法主要代表性方法为：自适应抵消和谱减法等[13-14]；统计方法主要代表性方法为：映射方法，参数估计和隐马尔科夫模型等[16-17]。但这方法在实际应用中还存在一些问题，如参数方法对所使用的模型依赖性强，需要提取模型参数；非参数方法不需要从传感器采集数据中估计模型参数，由于没有利用潜在的统计信息，不适合处理含非平稳背景噪声数据；统计方法充分利用了统计特点，以概率计算方法实现对信号的增强，但需要依赖一定准则实现对最优结构的选择。

如何应对低信噪比情况下、对未知多频带信号进行增强仍然是富有挑战性的难题。对此，本文提出一种基于滤波器组设计的多频带组合信号增强方法，该方法以人耳耳蜗时频分解原理为基础，设计了伽马通滤波器组，对传感器拾取数据进行分析处理，并根据信号与背景噪声在强度和稳定性上的差异，建立判决统计量，对各频带数据实现判决加权处理，在无需搜索单个滤波频带的情况下，提高了合成数据信噪比，实现了对未知多频带组合信号的增强，进而提升了能量累积检测方法对未知多频带组合信号的检测效果。

1 滤波器组设计

在人耳听觉系统中，不同频率的信号可在人耳耳蜗基底膜的不同位置产生最大响应[17-20]。对此，可依据人耳耳蜗基底膜频响特性，设计相应滤波器组模拟耳蜗基底膜频响特性，对传感器采集数据进行分解处理，增强未知多频带组合信号所在频带在整个处理频带中的比重。

在模拟人耳耳蜗基底膜时频分解中，本文采用一组相互交叠的伽马通滤波器组模拟实现，滤波器组的时域响应可表示为

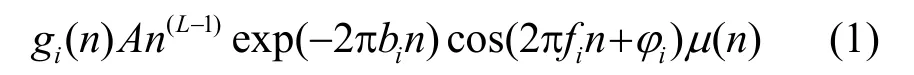
式中：n为采样点；A为滤波器组增益；L为滤波器组的阶数，本文取L=4，bi为第i个滤波器组衰减因子，1≤i≤I，I为滤波器个数；fi为第i个滤波器中心频率，φ为滤波器的初始相位，本文取φ=0，μ（n）为阶跃函数：

衰减因子bi决定了滤波器时域响应衰减速度，其与滤波器带宽有关，关系式为

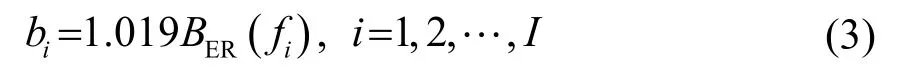
式中，BER（fi）为第i个滤波器等效矩形带宽，其表示形式为

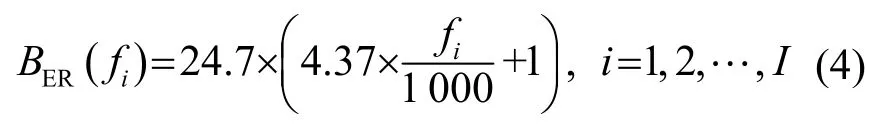
对于采样率为fs的数据拾取系统，在处理频带数确定的情况下，由式（3）和式（4）可得到第i个滤波器的中心频率fi，然后由式（1）可得到第i个滤波器的时域响应。

为了较为直观说明滤波器组的时频分解功能，图1给出了采样率fs=1 6 kHz时，在 1 Hz～8 kHz处理频率范围划分为I=2 4个滤波器所得时的频响应图。

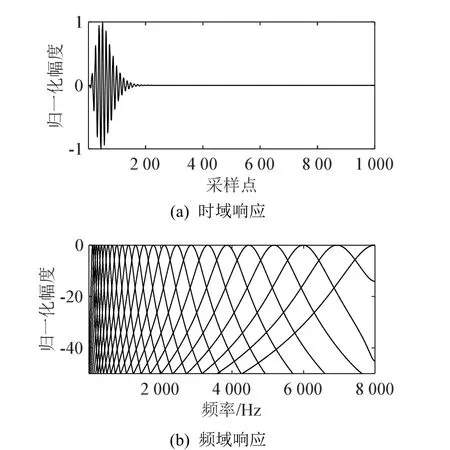
图1 伽马通滤波器组时频响应Fig.1 Time and frequency response curves of the Gammatone filter bank

由图1可知，滤波器组时域波形是一个振动频率等于其中心频率、振动包络为伽马函数曲线的波形[17]；各滤波器中心频率在等效矩形带宽域上等间距分布，然后映射到线性尺度，使各个Gammatonc滤波器的中心频率呈非线性分布，整个滤波器组的频率覆盖范围为0～8 kHz，可对处理数据实现时频分解；另外，每个滤波器都有一个特征频率点，在该频点位置响应最大，达到对响度补偿的最佳效果。同时每个滤波器均有一个拖尾（按指数衰减过程），在响应自身频带时，也可很好地兼顾相邻频带，有助于相邻频带之间的平滑。

2 未知多频带组合信号增强方法

2.1 判决处理

2.2 实现过程

如图2所示，传感器采集数据首先通过已设计的滤波器组进行分解，将其分解成与耳蜗非线性频率相对应的子带数据；然后，采用强度和稳定性信息形成判决统计量提取组成因子，构建判决统计量；最后，采用非线性判决加权方法对未知多频带组合信号增强。

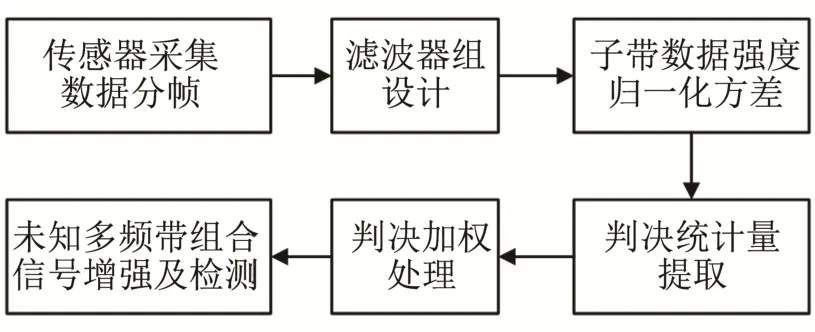
图2 未知多频带组合信号增强及检测流程图Fig.2 Flow chart of unknown multi-band combined signal enhancement and detection

本文方法具体实现过程可分为以下步骤：

输入：传感器拾取数据x（n），频带数I，滤波器组增益A和阶数L，分帧数M。

输出：增强信号zm，i（n），检测结果。

步骤（1）：对传感器采集数据进行分帧处理，得到本次处理数据xm（n）。

步骤（2）：按照式（1），设计滤波器组的时域响应函数。

步骤（3）：按式（5），对本帧处理数据xm（n）进行时频分解，得到各频带分解数据ym，i（n）。

步骤（4）：按式（6）计算ym，i（n）强度归一化方差Dδm，i，消除不同滤波器等效矩形带宽对判决统计量提取的影响。

步骤（5）：依据未知信号与背景噪声在各频带中的能量和稳定性归一化差异性，按式（7）建立判决统计量Ti。

步骤（6）：根据提取的各频带判决统计量Ti，对各频带数据ym，i（n）进行判决加权处理，并对其进行合成，得到信噪比较高的数据zm，i（n）。

步骤（7）：采用能量累积检测方法对zm，i（n）进行处理，实现对未知多频带组合信号的检测。

3 数值仿真分析

为了较为直观说明上述处理过程能够有效增强未知多频带组合信号，提升现有检测方法对未知信号的检测效果，进行数值仿真分析。系统的采样频率fs为16 kHz，未知信号个数为2，信号周期为1 s，1次处理数据长度为0.5 s，信号的仿真参数如表1所示。

表1 信号仿真参数Table 1 The parameters for simulated signal

仿真中，假定数据处理前对脉冲信号频带、脉宽长度均未知，所以在处理数据前只采用了带宽为100 Hz～8 kHz的128阶FIR滤波器对处理数据进行初始滤波处理。

图3、4给出了采用本文方法处理前后的数据对比。图5为本次处理中所得的判决统计量。处理中基于滤波器组中滤波器个数对频带宽度和运算量影响考虑（滤波器个数越多频带划分越细，但运算量也越大），所用滤波器组与图1所示一致。

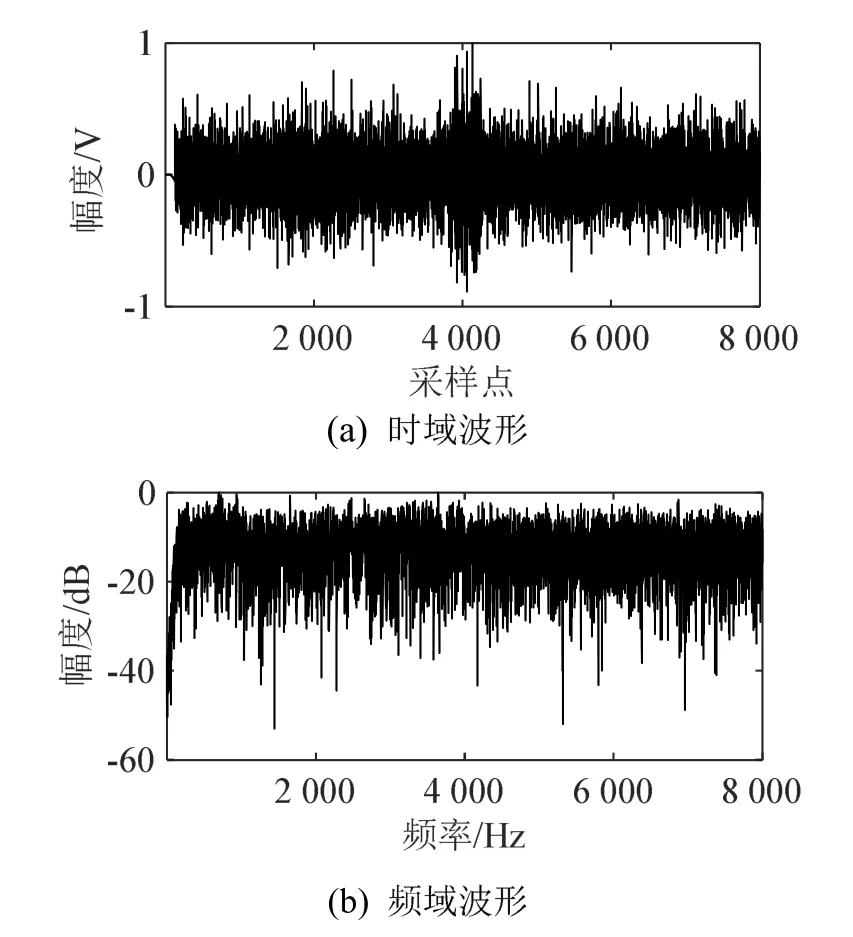
图3 FIR滤波后数据的时域波形和频谱Fig.3 Time domain waveform and frequency spectrum of the collected data after FIR filtering

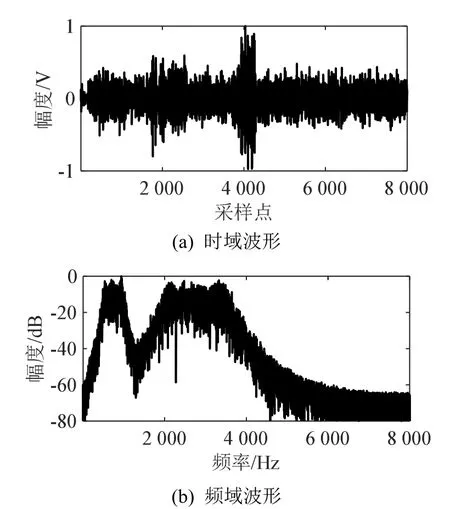
图4 本文方法处理后数据的时域波形和频谱Fig.4 Time domain waveform and frequency spectrum of the collected data after processing by the proposed method

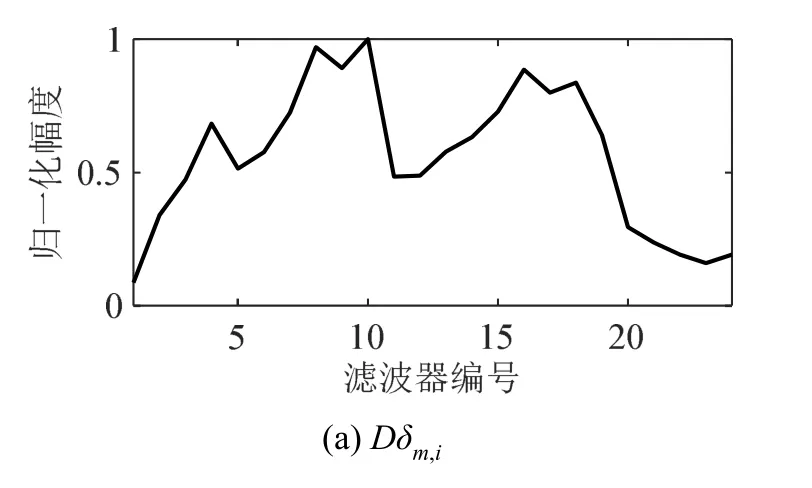
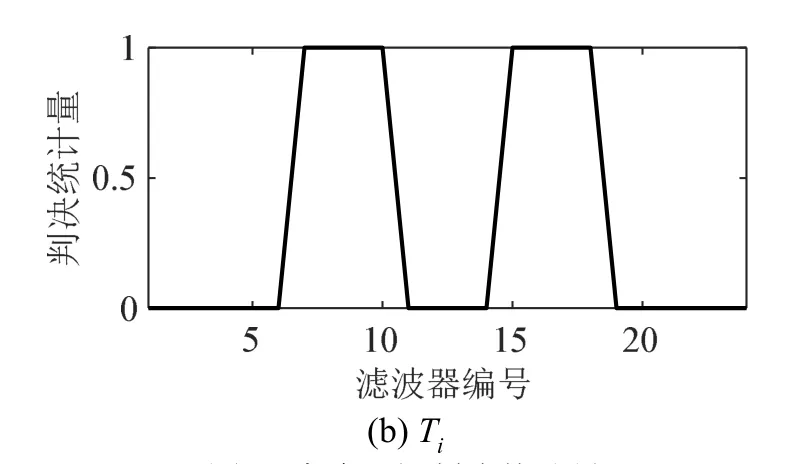
图5 滤波器组判决统计量Fig.5 Decision statistics of filter bank

为了便于从图中看出信号起止点与仿真参数中点起止是否一致，文中横坐标设置为采样点数。

由图3可见，并不能确定是否只有第4 000个采样点附近有脉冲；不能确定第4 000个采样点附近的脉冲信号带宽；由于在频谱图中不能明显看出信号所在频带位置，不确定是否能够采用单个FIR滤波器实现数据中的信号净化，无法通过频域滤波方法实现信号增强。

由图4可见，在多频带组合信号未知的情况下，采用本文方法处理可有效滤波处理数据中的噪声，能够区分第2 000个采样点和第4 000个采样点附近频带脉冲信号所在位置及其频带范围，提高了数据中多频带组合信号信噪比。同时，由图1和图5可知，判决统计量为1时对应滤波器编号所含的频率范围包含信号频率范围 0.5～1 kHz 和 2～3.5 kHz。该仿真结果证实了本文方法能够在低信噪比情况下对未知多频带组合信号实现增强。

为了进一步说明本文方法有助于现有信号检测方法实现对未知信号的检测。图6给出了直接采用能量累积检测法检测的未知信号结果，图7给出了经本文方法处理后，再采用能量累积检测法对未知多频带组合信号检测结果。

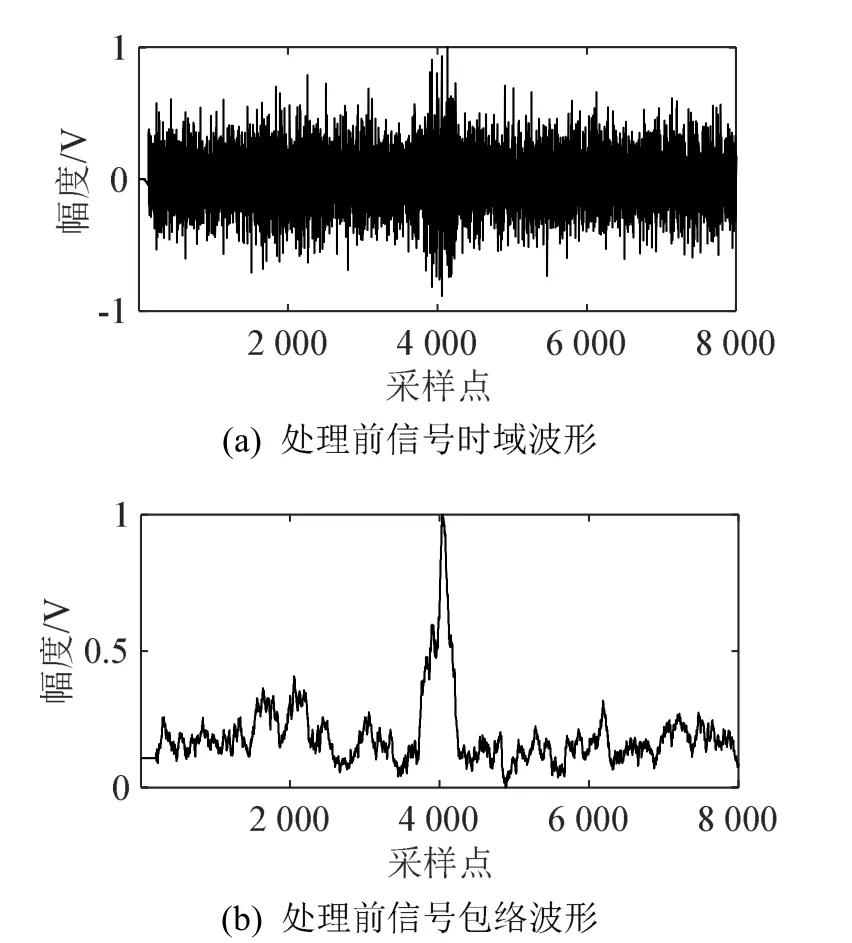
图6 本文方法处理前未知组合信号检测Fig.6 The signal detection result before processing by the proposed method

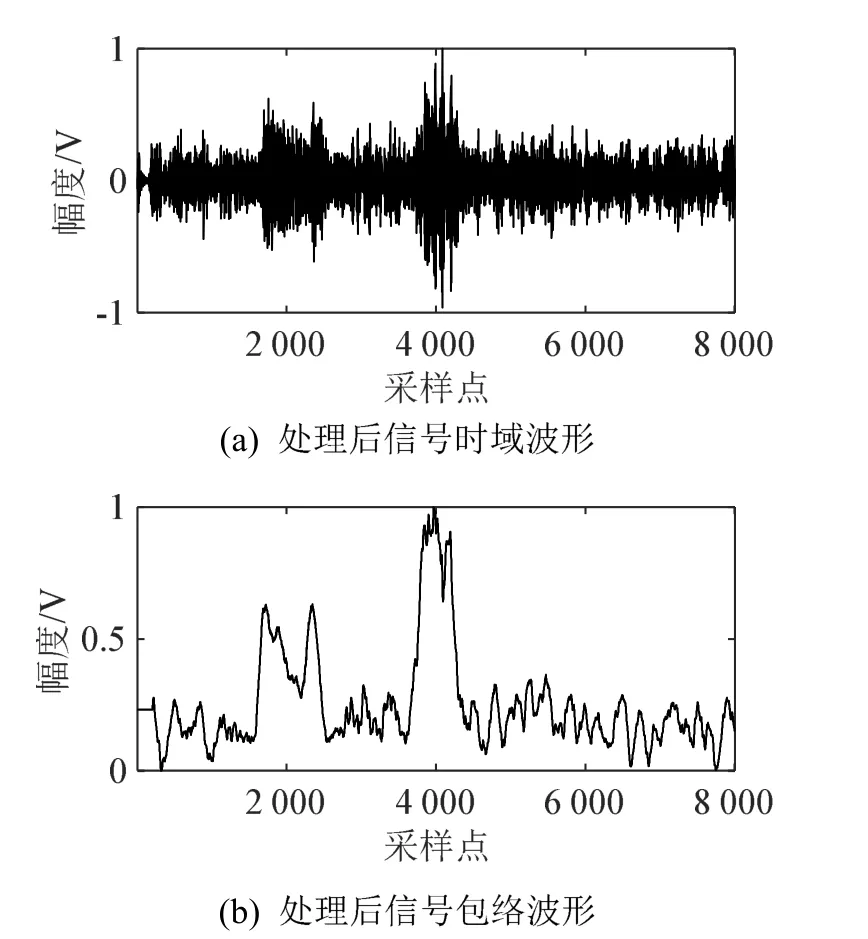
图7 本文方法处理后未知组合信号检测结果Fig.7 The signal detection result after processing by the proposed method

由图6和图7的结果可知，采用能量累积检测法无法对原始数据（经过FIR滤波器滤波处理）进行多频带组合信号检测，无法对第2 000个采样点附近未知脉冲信号实现检测；而经本文方法处理后，再采用能量累积检测法对其进行检测，可有效实现对第2 000个采样点和第4 000个采样点附近的脉冲信号检测。该结果进一步证实了本文方法可提升信号检测方法对未知多频带组合信号的检测效果。

另外，为了进一步说明本文方法可对未知多频带组合信号实现信噪比提升，本文采用信噪比（Signal to Noisc Ratio， SNR）作为评价指标，对采用本文方法处理效果进行定量分析，计算公式为

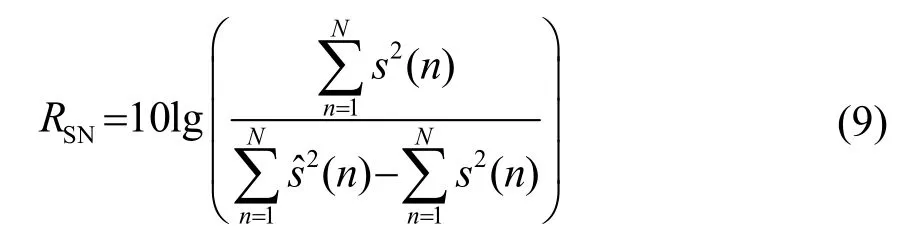
式中，s（n）为未知信号，为经本文方法处理前后数据。

由式（9）计算可得，对于图3中第2 000个采样点附近的脉冲信号，信噪比约为-8.5 dB，经本文方法处理后，其信噪比约为3.3 dB。该结果表明，在该仿真条件下，经本文方法处理后，信噪比提高了约12 dB。

图8为由200次独立统计所得传感器采集数据在不同输入信噪比的情况下，经滤波器组判决统计处理所得的数据信噪比。

图8 不同输入信噪时，经本文方法处理后输出信噪比Fig.8 The output signal to noise ratios after processing by the proposed method under different input signal to noise ratios

由图8可知，经本文方法处理，输出信噪比与输入信噪比之差最小为6 dB，可有效提升数据中未知多频带组合信号信噪比。该结果进一步验证了本文方法的有效性和可行性。

4 结 论

针对低信噪比情况下未知多频带组合信号增强及其检测问题，本文首先介绍了伽马通滤波器组设计原理及其具有的时频分解功能；然后利用信号与背景噪声在强度和稳定性上的差异性，建立判决统计量实现对待处理数据进行判决加权处理，在无需搜索单个滤波频带的情况下，提升数据中未知频带信号信噪比。在本文仿真条件下，本文方法能够将未知多频带组合信号信噪比提升6 dB以上，在信号频带未知的情况下，实现了对多频带组合信号增强，提升了能量累积检测方法对未知多频带组合信号检测效果。