双层介质声传播问题的标准解及有限元解

周益清，骆文于，吴双林

（1. 中国科学院声学研究所声场声信息国家重点实验室，北京 100190；2. 中国科学院大学，北京 100049）

0 引 言

自20世纪60年代以来，国内外学者对声场计算方法进行了大量的研究，先后出现了许多种针对水下声传播的计算模型。目前比较流行的几种声场计算方法有：射线法[1-2]、简正波法[3-4]、抛物方程法[5-6]、波数积分法[7-8]，研究人员使用这些方法建立了许多声场计算模型，但是目前还没有非常流行的有限元算法模型。可见，关于有限元方法在水下声场计算中的研究还不是非常充分。

有限元方法是求解偏微分方程复杂边值问题的一种通用数值解法。它首先将物理域离散成有限数量的单元，各单元以节点相连，然后利用各单元间的关联性形成一系列的有限元方程组，求得单元内的精确解或近似解，从而把复杂的偏微分方程边值问题转化为大型方程组的求解问题[9]。在水声学中，目前有限元方法主要被用来分析换能器的结构振动、解决声散射问题[10]，而关于声传播的研究[11-12]相对较少。

由于过去的计算机性能较现在落后很多，且我们常关心大尺度的声传播问题对计算机的计算速度和内存的要求都很高，所以过去的水下声传播方向的学者对有限元方法的研究较少。但是，近些年，随着计算机软硬件的快速发展，已经有充分的条件使用有限元方法进行水下声传播的研究。因此，希望开发一个基于有限元方法的声场计算模型，以处理复杂边界下的实际水下声传播问题。

本文主要研究双层介质中的声传播问题。首先，讨论有限深度的双层介质中的声场计算，使用波数积分方法计算出标准解后，再使用有限元方法计算相同问题的声场，对于出射边界，我们分别选择传统辐射条件、Dirichlct to Ncumann （DtN）非局部算子和完美匹配层来处理，经过对比，发现使用完美匹配层方法处理出射边界精度更高。然后，讨论无限深度的双层介质，即 Pckcris波导中的声场计算，这里同样使用波数积分方法计算标准解，再与结合了完美匹配层技术的有限元方法以及常用的简正波模型KRAKEN进行对比。我们发现，当某号简正波的本征值非常接近割线时，KRAKEN可能无法对该本征值进行准确求解，从而导致较大的计算误差。但是有限元方法则不受此类限制，所以相比KRAKEN而言，有限元方法的普适性更优。

1 问题描述

1.1 有限深度的双层介质问题

如图1所示为有限深度的双层介质，上层介质的下边界深度为D1，声速和密度分别为c1，ρ1，下层介质的下边界深度为D2，声速和密度分别为c2，ρ2。在z=0处为绝对软的上边界，声压为0；在z=D2处为绝对硬的下边界，质点法向振速为0。对于无限大三维介质中的无限长线声源，可以将它简化为图1所示的二维问题，假设声源位于第一层介质中，深度为zs。

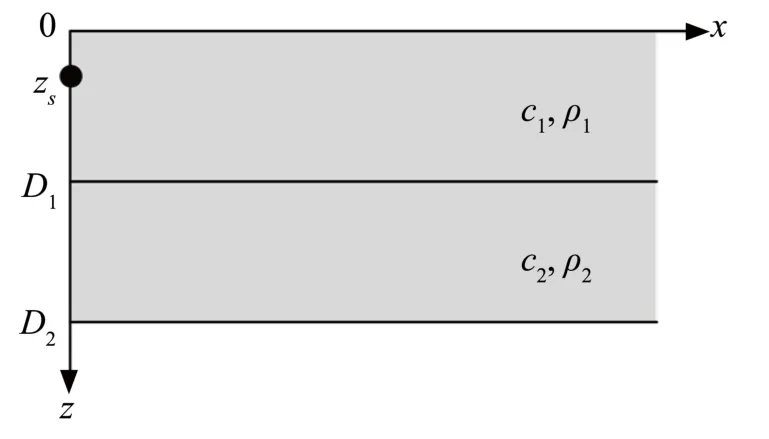
图1 有限深度的双层介质环境示意图Fig.1 Schematic diagram of a two-layer medium with bothlimited depths

1.2 无限深度的双层介质问题

如图2所示为无限深度的分层介质，即Pckcris波导。上层介质的下边界深度为D1，声速和密度分别为c1，ρ1，下层介质厚度无限大，声速和密度分别为c2，ρ2。在z=0 处为绝对软的上边界，声压为0。对于无限大三维介质中的无限长线声源，同样可以将它简化为图2所示的二维问题，声源深度为zs，假设位于第一层介质中。

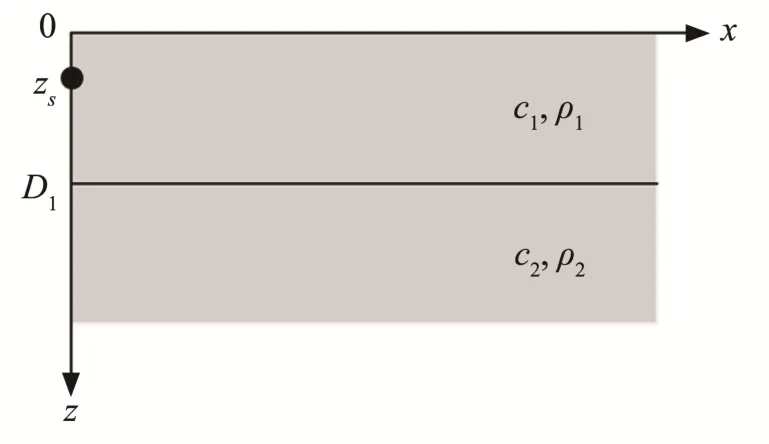
图2 无限深度的双层介质环境示意图Fig.2 Schematic diagram of a two-layer medium with an unlimited depth

由于这两个问题都不存在解析解，所以我们使用波数积分方法推导出标准解，用于与其他方法进行比对。

2 使用波数积分法计算标准解

2.1 有限深度的双层介质的标准解

对于图1所示的无限长线源问题，选用直角坐标系（x，z），z轴通过声源且垂直向下，x轴平行于海面，此时线源的Hclmholtz方程表示为[9]

其中，ψ（x，z）表示位移势。对于线源问题，利用傅里叶变换对：

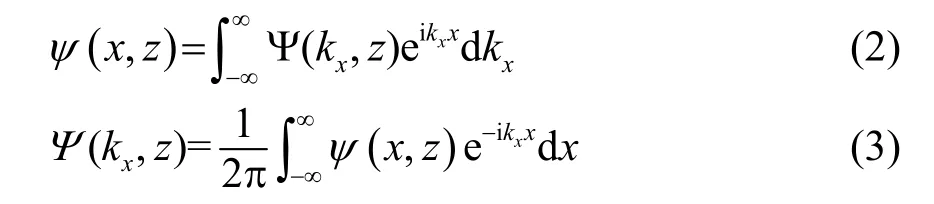
得到如下形式的深度分离波动方程：

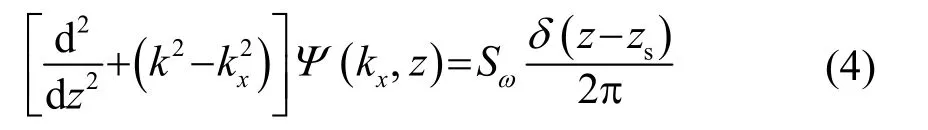
带入边界条件，求解该方程，得到深度格林函数Ψ（kx，z），利用逆傅里叶变换求得位移势ψ（x，z），进而求得总声场。

对于深度分离的波动方程，我们只需要考虑介质中的上行波及下行波。图3为双层介质中的上行波与下行波示意图，在每层介质中，都分别包含上行波与下行波。其中，上层介质中的下行波幅值记为，上行波幅值记为；下层介质中的下行波幅值记为，上行波幅值记为。

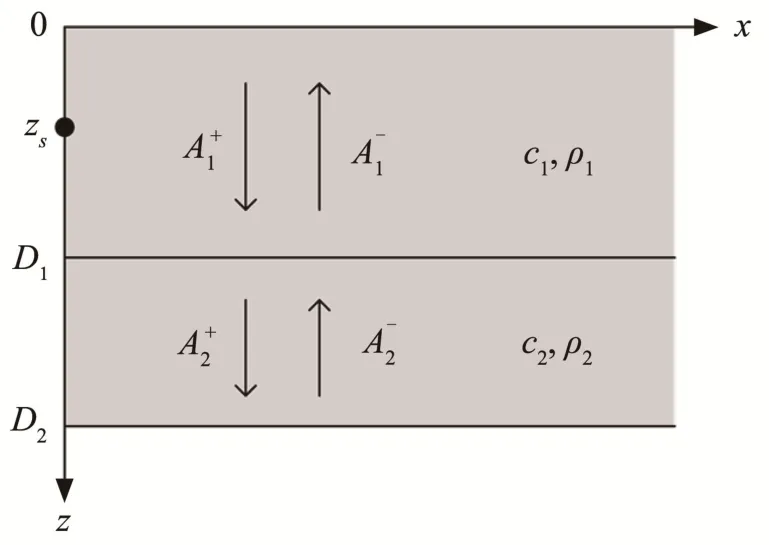
图3 有限深度双层介质中上行波与下行波示意图Fig.3 Schematic diagram of up-going and down-going waves in the two-layer medium with both limited depths

2.2 无限深度的双层介质的标准解

对于无限深度的双层介质，即 Pckcris波导中的声场，同样也是首先求解式（4）中的深度分离的波动方程。

对于深度分离的波动方程，只需要考虑上行波及下行波。图4表示双层介质中的上行波与下行波示意图，在上层介质中，既包含上行波，又包含下行波；而在下层介质中，只存在下行波。其中，上层介质中的下行波幅值记为，上行波幅值记为；下层介质中下行波幅值记为。

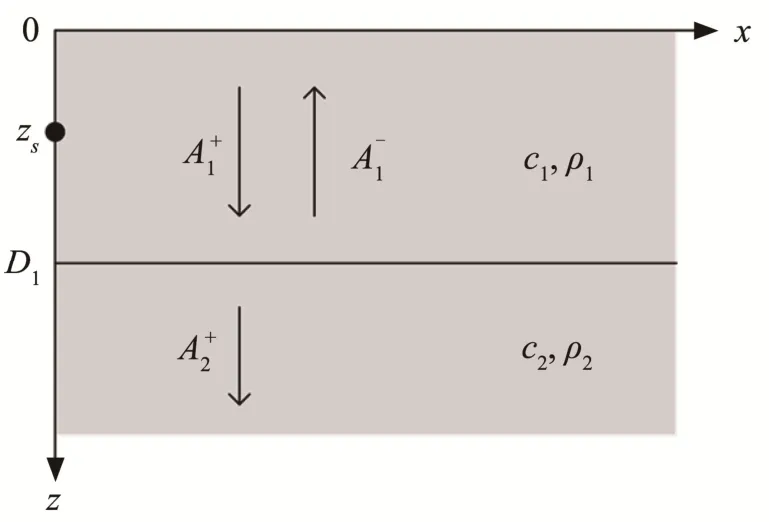
图4 无限深度双层介质中上行波与下行波模拟示意图Fig.4 Schematic diagram of up-going and down-going waves in the two-layer medium with an unlimited depth

3 使用有限元方法计算声场

使用有限元方法计算声场主要分为以下步骤：（1） 将物理域离散为许多小的计算单元；（2） 根据单元的形状和结点数构造形函数；（3） 写出近似解表达式；（4） 推导出离散的有限元方程；（5） 建立单元刚度矩阵和单元外载荷向量；合成总体刚度矩阵和载荷向量；（6） 带入边界条件求解声场；（7） 后处理和误差分析。

3.1 有限元方程的推导

3.2 计算区域离散后的有限元方程

由于计算区域形状规则，所以采用四节点四边形单元对计算区域进行离散。同时，四节点四边形单元比三节点三角形单元具有更高的精度，拥有更高阶的连续性。四节点四边形单元如图5所示，单元中点坐标为 （x0，z0） ，单元的长和宽分别为2a，2b。

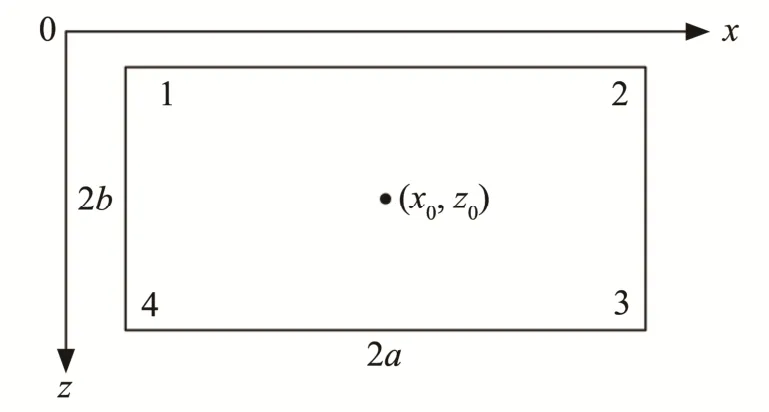
图5 四节点四边形单元的局部编号、中点坐标、长度与宽度示意图Fig.5 Schematic illustration of local number, midpoint coordinates, length and width of the four-node quadrilateral element

用函数Nn（x，z） 表示形函数，其中n=1 ，2，3，4分

3.3 出射边界的处理

在水下声传播计算方面，有限元方法面对的最大的挑战之一是如何模拟没有边界的无限大海洋环境，即满足无限远处的Sommcrfcld辐射条件[13]：

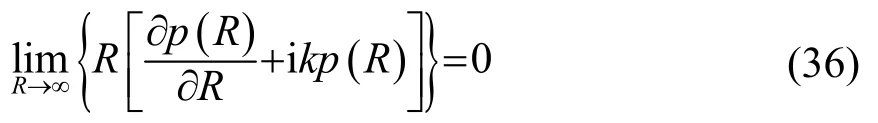
其中：R表示距离；k表示波数；p表示声压。下面，分别使用三种常用的出射边界计算方法来求解声场。

3.3.1 传统辐射条件

传统的辐射条件是指：待求量的径向导数等于待求量在声源一定距离处的值与常数的乘积。对于本文讨论的双层介质中的声传播问题，可以将右侧出射边界用传统辐射条件表示为

代入式（30）的第一项，可以得到：

将式（33）中的声压p和式（34）中的试验函数q代入式（38）即可求得最右侧单元对应的单元刚度矩阵。

最后，利用式（35）计算得到的单元刚度矩阵，在集成总体刚度矩阵时，将每个单元的局部坐标与总体坐标一一对应，即可得到总体刚度矩阵。

3.3.2 DtN非局部算子

传统辐射条件并不能完全吸收出射波，回波会干扰声场，产生误差。1978年，Fix和 Marin[14]对轴对称情况下的分层介质中的声场进行了研究，并且第一次提出了非局部算子，同时指出了非局部算子相对于传统辐射条件的优越性。

3.3.3 完美匹配层

传统辐射条件可能会引入较大误差，非局部算子会改变全局刚度矩阵的稀疏性。下面引入完美匹配层，在保持刚度矩阵稀疏性的同时，尽量减小误差。

完美匹配层是Bcrcngcr[15-16]在1994年提出的一种概念，希望用它来模拟出射边界，使得只有少量的能量甚至没有任何能量反射回我们计算的物理场中。

如图6所示，对于深度有限的双层介质，我们设需要计算的物理域的水平距离为R，在物理域的右侧设置一个厚度为δx的完美匹配层。如图6中右侧PML1和PML2所示，完美匹配层中的声速和密度与相邻的左侧介质相同。

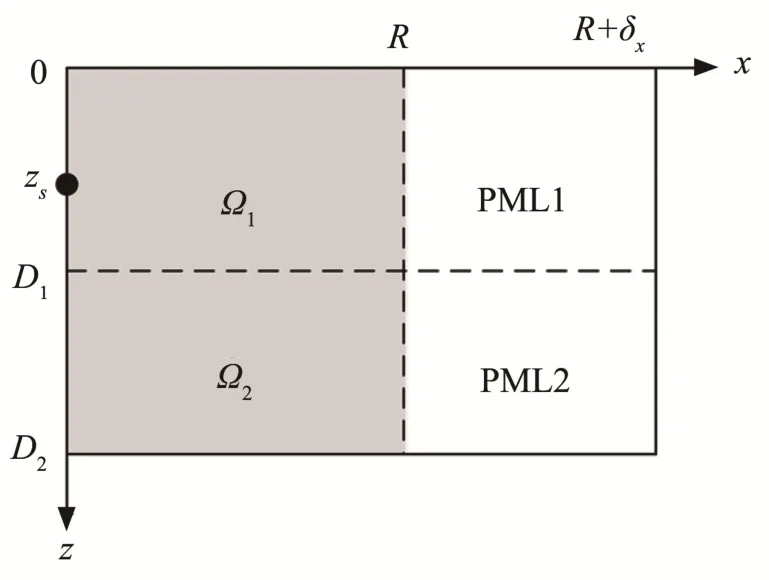
图6 添加完美匹配层的有限深度双层介质示意图Fig.6 Schematic diagram of two-layered medium with both limited depths plus perfectly matched layers

而对于无限深度的双层介质，设需要计算的物理域的水平距离为R，深度为D2，在物理域的右侧设置一个厚度为δx的完美匹配层，在物理域的下侧设置一个厚度为δz的完美匹配层，如图7所示。

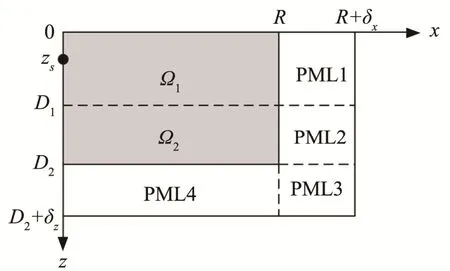
图7 添加完美匹配层的无限深度双层介质示意图Fig.7 Schematic diagram of two-layer medium with an unlimited depth plus perfectly matched layers

3.4 其他边界条件的处理

对于左侧边界，即x=0处，满足对称条件，可视作位移为零的绝对硬边界；对于有限深度的双层介质z=D2处的下边界也是绝对硬边界；z=0 处的上边界是绝对软边界，声压p=0 。

对于绝对硬边界，法向位移为0，即∂p/∂n=0，对刚度矩阵贡献为0，不用进行特殊的处理和计算。对绝对软边界，我们采用“对角元素置 1”法进行计算，步骤如下：

（1） 设总体刚度矩阵为K，其元素可以表示为Kmn，外载荷向量为f，声压向量为p，它们满足线性方程组Kp=f，设绝对软边界的节点总体编号为l。

（2） 将K的第l列与第l行置零，第l个对角元素置1。

（3） 将f的第l个元素设置为 0。

（4） 得到更新后的线性方程组Kp=f，求解即可得到每个节点处的声压。

4 计算结果

4.1 有限深度双层介质中的声场

取如图8所示的环境参数，上层介质的厚度为 60 m，声速c1=1500 m· s-1，密度ρ1=1 000 kg·m-3，下层介质厚度为 40 m，声速c2=1800 m· s-1，密度ρ2=1 800 kg·m-3，声源深度为20 m。

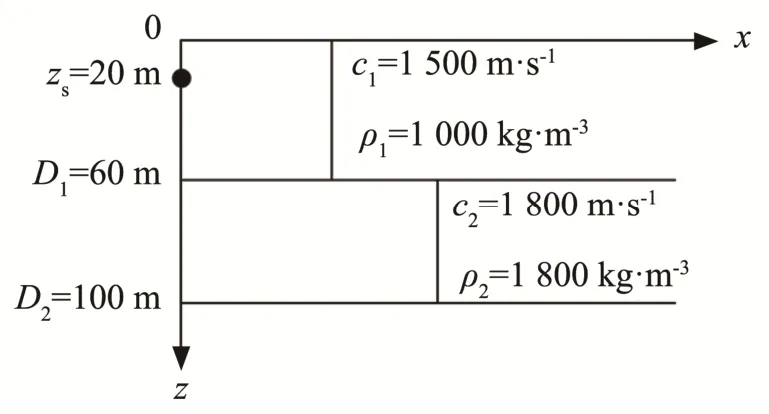
图8 双层介质环境参数示意图Fig.8 Specific environmental parameters of a two-layer medium

图9表示使用不同方法计算的25 Hz声源产生的声场。其中，图9（a）为使用波数积分方法计算得到的解，可视为标准解。图9（b）是使用传统辐射条件处理出射边界的有限元解。可以看出有限元解与标准解的图案基本一致，但是在水平方向存在明显的干涉条纹。这是由于传统辐射条件没有完全吸收出射波，向右传播的出射波与向左传播的反射波产生干涉现象，从而引入了误差。图9（c）是使用DtN非局部算子处理出射边界的有限元解。可以看到，相比传统辐射条件而言，干涉现象有了轻微的削弱，但是依然存在，且不可忽略。同时，DtN非局部算子只能用于处理单向出射边界，即难以处理可穿透海底的问题。图9（d）是使用完美匹配层处理出射边界的有限元解，可以看到，该计算结果与标准解吻合得较好。

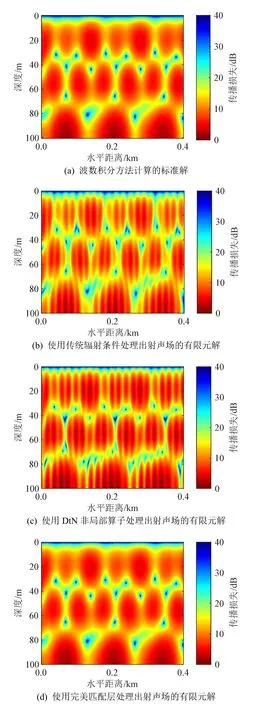
图9 声源频率为25 Hz时使用不同方法计算的双层介质中的声场Fig.9 Sound field diagrams in the two-layer medium calculated by different methods at 25 Hz

图10表示深度为48 m处的传播损失。该深度下，有限元解和标准解的平均误差为 0.09 dB，两组计算结果吻合得较好。

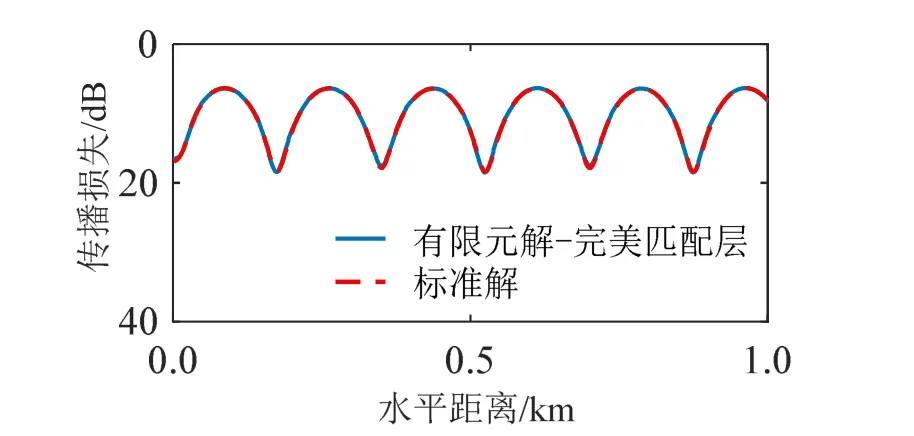
图10 声源频率为25 Hz时接收深度48 m处的传播损失Fig.10 Transmission loss at 25 Hz and at the receiving depth of 48 m

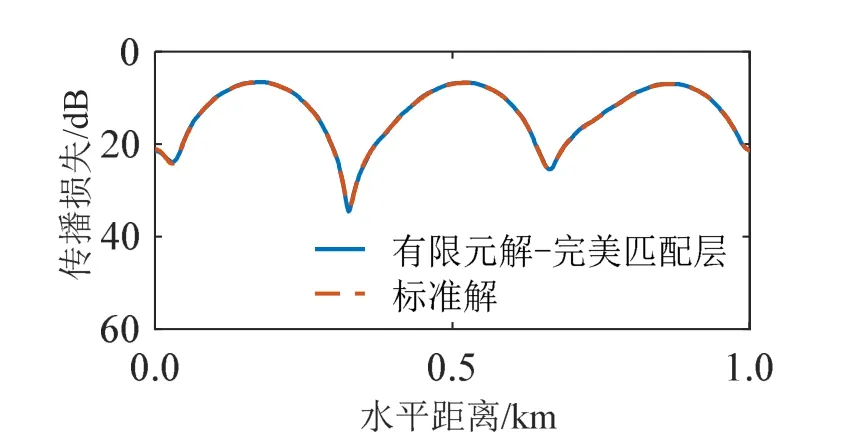
图11 声源频率为25 Hz时接收深度80 m处的传播损失Fig.11 Transmission loss at 25 Hz and at the receiving depth of 80 m

从以上结果可以看出，本文所提的有限元模型计算得到的结果与标准解吻合得较好。下面我们需要验证，对于更高的频率，该有限元模型是否依然具有较高的精度。

图12表示声源频率为100 Hz时分别使用波数积分方法和有限元方法计算的声场，其中图12（a）表示使用波数积分方法计算得到的声场标准解，图12（b）是使用完美匹配层处理出射边界的有限元解。从计算结果可以看出，本文所提的有限元解与波数积分方法计算的标准解吻合得较好。

图12 声源频率为100 Hz时使用不同方法计算的双层介质中的声场Fig.12 Sound field diagrams in the two-layer medium calculated by different methods at 100 Hz

图13为深度60 m处的传播损失。该深度下，因为存在一个传播损失波谷，所以有限元解和标准解的平均误差稍大，近似为0.19 dB。两组计算结果总体上吻合得较好。

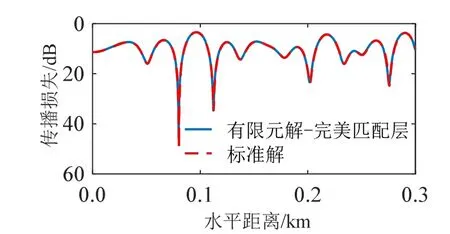
图13 声源频率为100 Hz时接收深度60 m处的传播损失Fig.13 Transmission loss at 100 Hz and at the receiving depth of 60 m

4.2 无限深度双层介质中的声场

对于无限深度的双层介质，即 Pckcris波导，我们取如图14所示的环境参数，上层介质的厚度为40 m，声速c1=1500 m· s-1，密度ρ1=1 000 kg·m-3；下层介质无限大，声速c2=1650 m· s-1，密度ρ2=1 500 kg·m-3。声源深度为20 m，接收深度为40 m。

图14 无限深度双层介质环境参数示意图Fig.14 Specific environmental parameters of a two-layer medium with an unlimited depth

首先计算声源频率为105～125 Hz的传播损失。如图15所示为不同声源频率在接收深度40 m处的传播损失，其中图15（a）为常用的简正波模型KRAKEN计算的传播损失，图15（b）为使用波数积分方法推导出的标准解，图15（c）为使用有限元方法计算的传播损失。从图15可以看出，有限元解与波数积分方法计算的标准解吻合得较好，而KRAKEN计算的结果在某些频率上存在显著误差，这是由于对声场有主要贡献的某号本征值位于割线附近时，KRAKEN无法准确计算该号本征值导致的[18]。可以看出在声源频率为 112、118 Hz时，KRAKEN计算的传播损失与另外两种方法计算的传播损失有明显的差别。下面分别分析这两个频率处的本征值与传播损失的关系。

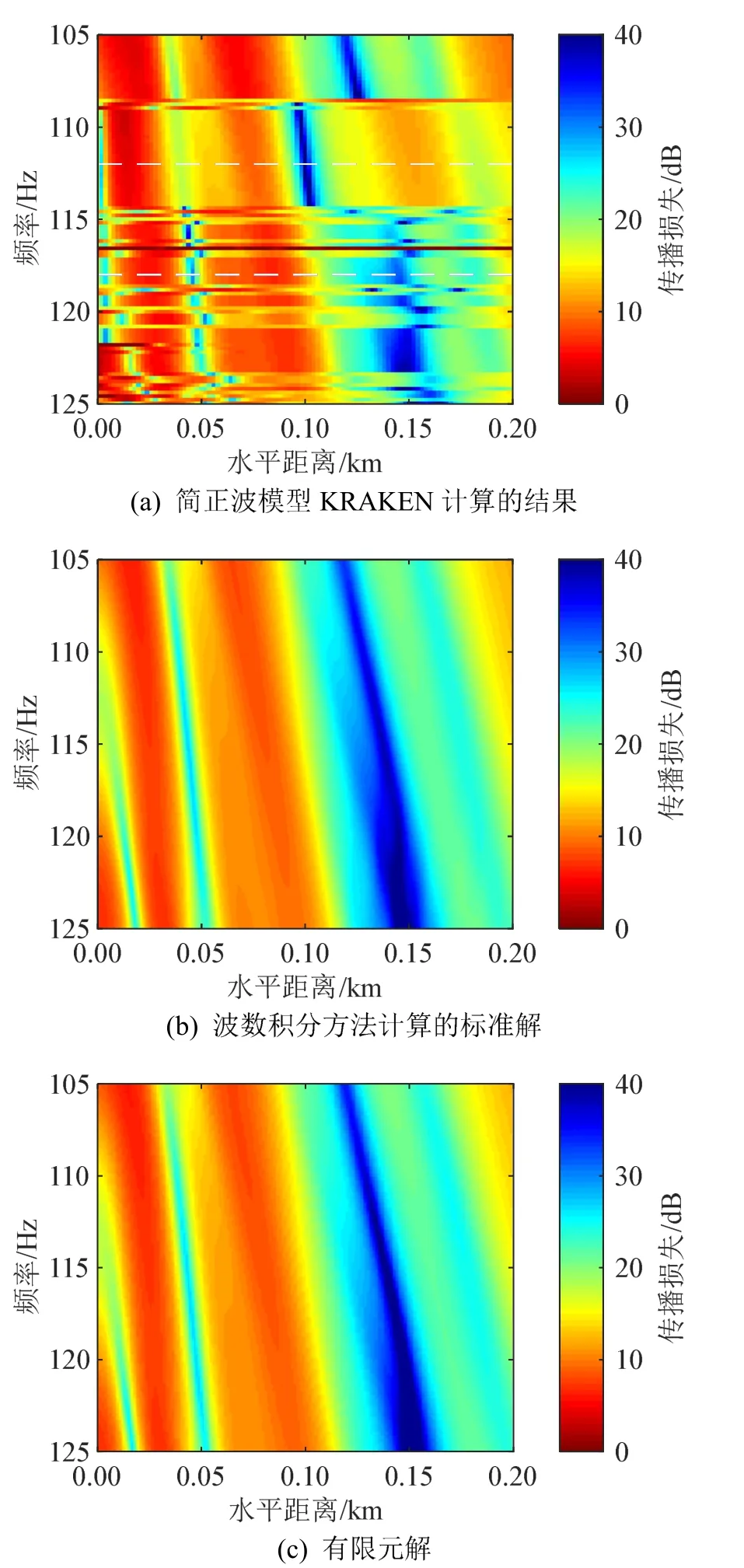
图15 声源频率为105～125 Hz时不同方法计算的接收深度为40 m处的传播损失Fig.15 Transmission loss diagrams calculated by different methods at the receiving depth of 40 m and at the frequencies from 105 to 125 Hz

图16为不同声源频率时使用波数积分方法计算的深度格林函数。图16（a）中声源频率为112 Hz，对应的下层介质波数约为0.426 5 m-1。在这个频率下，KRAKEN得到的前五号简正波的水平波数（即本征值）分别为 0.464 455、0.449 802、0.381 011+i0.009 161、0.309 880+i0.017 855、0.188 504+i0.039 225，对于当前问题，由于第3号简正波的水平波数与海底波数非常接近，KRAKEN未能计算出该号简正波，从而导致KRAKEN模型的传播损失结果出现了较大的误差。图16（b）中声源频率为 118 Hz，对应的下层介质波数约为0.449 3 m-1。在此频率下，KRAKEN得到的前五号简正波的水平波数分别为 0.489 759、0.475 685、0.451 877、0.411 541+i0.007 906、0.346 650+i0.015 463。比较简正波的水平波数与图16（b）可以发现，声源频率为118 Hz时，第3号简正波的水平波数与海底波数的差异足够大，KRAKEN可以准确求出这号简正波，因此在声源频率为118 Hz时，KRAKEN计算结果与标准解的一致性非常好。

图16 不同声源频率对应的深度为40 m处的深度格林函数，Fig.16 Magnitudes of the depth-dependent Green’s functions at the depth 40 m and at the frequencies of 112 Hz and 118 Hz

然后分别对声源频率为112、118 Hz时，三种不同方法计算的传播损失进行比较。图17（a）、17（b）分别为声源频率为112、118 Hz时接收深度40 m处的传播损失。可以看到，声源频率为 112 Hz时，KRAKEN遗漏了有主要贡献的第三号简正波，导致计算误差较大，而有限元方法不需要计算简正波，与标准解吻合得非常好。声源频率为 118 Hz时，KRAKEN包含了前三号有主要贡献的简正波，所以与有限元解和标准解吻合得非常好。

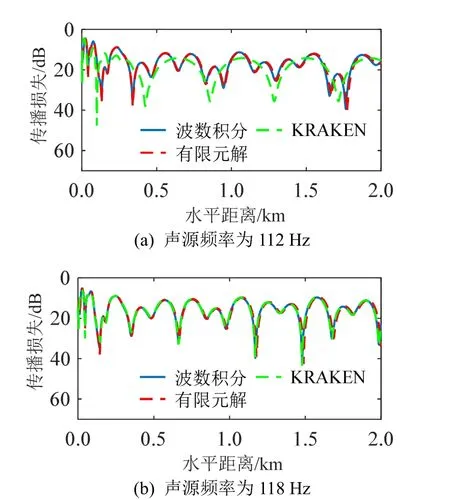
图17 不同方法计算的在40 m深度不同声源频率传播损失结果Fig.17 Transmission losses calculated by different methods at the depth of 40 m and at the frequencies of 112 Hz and 118 Hz

通过对比发现，简正波模型KRAKEN需要求解简正波，而在一些特定的情况下，可能会遗漏对声场有主要贡献的简正波，从而产生较大误差。而有限元模型不需要求解简正波，所以对几乎所有频率都具有较高的精度，即有限元方法的普适性优于简正波方法。

5 结 论

本文研究了双层介质中的声传播问题，分别讨论了有限深度的双层介质和无限深度的双层介质的情况。

由于有限深度双层介质问题不存在解析解，因此首先使用波数积分方法推导出标准解。然后提出一个有限元模型，并研究不同出射边界的处理方法对有限元解的影响，发现传统辐射条件会引入较大的误差，非局部算子会破坏总体刚度矩阵的稀疏性，而且不适用于沿不同方向出射的声波，而完美匹配层拥有较高的精度，且不会破坏总体刚度矩阵的稀疏性，使用也十分灵活。本文所提的有限元模型选取精度最高、使用方法最灵活的完美匹配层方法来处理出射声场，并进行后续计算。数值结果表明本文所提的有限元解和标准解吻合较好。

对于无限深度的双层介质，同样先使用波数积分方法推导出标准解，然后分别使用本文所开发的结合了完美匹配层的有限元模型和常用的简正波模型KRAKEN，计算不同频率下的声场。研究发现在一些特定的频率，由于KRAKEN在计算时遗漏了一些对声场有主要贡献的简正波，会产生明显的误差。而有限元方法不需要计算简正波，因此在各频率都与标准解吻合得较好。

本文基于传统的Galcrkin方法推导出水下声传播有限元方程，然后使用完美匹配层处理出射声场，设计并实现了一个水下声场计算有限元模型。通过该模型计算得到的双层介质中的声场，与标准解吻合得较好。同时，由于有限元方法不需要求解简正波，因此对于某些简正波方法不能准确处理的问题，有限元方法仍能给出准确的声场结果，表明有限元方法的普适性优于简正波方法。

值得一提的是，有限元方法的优缺点都非常突出，优点在于普适性强且精度高，缺点在于计算量大且物理意义不清晰。因此，本文选择研究有限元方法并非是希望建立一个通用的声场计算模型来解决实际应用中的声传播问题，而是希望使用有限元方法提供参考解，来优化其他声场计算模型。例如，在计算复杂海洋环境中的声场时，如复杂地形或内波等问题，很难验证现有模型的计算结果的正确性，这时就可以使用有限元方法提供标准解，用于校验现有模型的结果，从而对其进行改进，使其适用于解决更加复杂的环境中的声场问题。

本文的内容是有限元方法在水下声场计算中的一些初步工作，接下来将对本文所提的有限元声场计算模型进一步改进，提升模型精度，并使之可以计算更加复杂环境中的声场。