基于舰船噪声的海底单参数反演

曹启旻，赵 梅，胡长青

（1. 中国科学院声学研究所东海研究站，上海 201815；2. 中国科学院大学，北京 100049）

0 引 言

海洋环境中存在着大量的舰船噪声，尤其是在浅海海域存在大量的渔船、货船等，其辐射噪声在传播过程中不断地与海底和海面接触，携带大量关于海底底质的信息，因此利用舰船噪声反演海底底质信息成为可能。

1985年，Kupcrman等[1]第一次将水听器阵接收到的船噪声数据进行波束形成处理，并进行地声参数反演。国内对于舰船噪声的反演最初是 2007年张仁和教授的团队利用一次实验中测量的船辐射噪声数据获得了不同距离下的相干传播损失，并反演了海底吸收系数[2]。任群言等[3]利用波导特征阻抗比反演声呐预报中的海底和沉积层的地声参数，通过干涉方法快速估计沉积层声速和厚度的变化规律。深海方面，薄连坤等[4]研究了利用拖曳阵接收拖船低频噪声对深海声学参数进行近场匹配场反演（Matchcd-Ficld Invcrsion， MFI）的方法。在目标识别领域，郭政等[5]提出了一种支持向量机递归特征消除快速筛选出部分优质特征子集与猫群算法迭代寻优结合的特征选择方法。

2012年，胡长青团队根据大量观测数据中小掠射角下反射损失随掠射角近似线性增长的规律[6]，提出以反射损失随掠射角的变化率FdB为反演单参数。图1为文献中三种典型沉积物的海底反射损失值[7]。利用海底密度等基本参数拟合出单参数FdB，证实单参数假设合理且能反映海底性质。之后该团队进一步分别得到了在均匀浅海和负跃层条件下，利用海底单参数模型描述水下声场的方法[8-9]。屈科等基于海底单参数模型，设计出了一系列时域反演方法，包括利用脉冲波形反演、基于传播损失反演，并利用北黄海和东中国海实验数据予以论证[10-11]。赵梅设计出了一种海底单参数频域反演方法[12]，并应用该方法对东中国海域实验数据进行了实际反演，通过传播损失预报以及海底采样结果验证了该频域反演方法的有效性。进一步利用频域方法反演得到的单参数结果，对实验海域海底沉积物进行了分类应用。陈勃等提出了一种建立在单个参数海底模型基础上的噪声空间相干系数计算方法[13]。

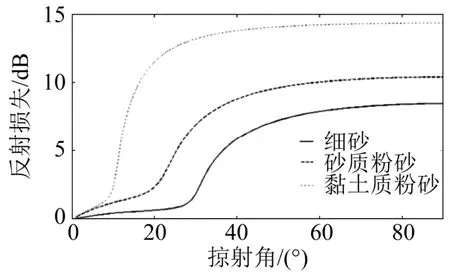
图1 三种沉积物的海底反射损失Fig.1 Seabed reflection losses of three different types of sediments

但以往的舰船噪声反演地声参数方法，依赖于多维参数模型，并且部分需要大量寻优。本文结合单参数模型，仅需要单个水听器接收到的舰船噪声数据便可对海底底质进行反演。

1 理论计算

1.1 单参数模型介绍

假设海底是符合 Hamilton反射规律的半无限大液态海底，可以用密度、压缩波声速和衰减系数表示。以单参数FdB（dB·rad-1）表示小掠射角下海底反射损失LB随角度θ的变化率[6]：

从海底声阻抗出发，经推导可得到单参数FdB的表达式[7]为

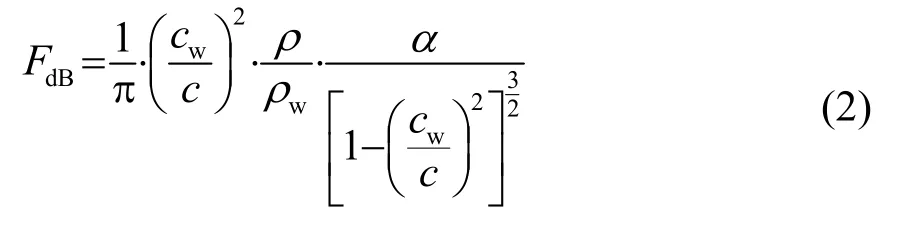
其中：c为海底沉积物声速；α为衰减系数；ρ为海底沉积物密度；ρw为海水密度，cw为海水声速。

单参数也可以用指数形式F表示，将反射后声强I与入射声强I0关系：I=I0c xp （-Fθ），代入海底反射损失的表达式LB=10lg （I/I0）可以得到单参数的分贝形式FdB和指数形式F之间的换算关系式[6]：

在液态无限大均匀海底模型中，根据之前的研究[10]，在柱面扩展、球面扩展、柱面扩展附加海底衰减单号简正波区域中、3/2次多号简正波干涉区，适用于单参数模型的多号简正波干涉区（衰减区间为：）中对海底单参数进行反演可近似表达为简单的关系式[11]：

实验中只需要单个水听器接收到的数据，结合实验时声源的距离r和实验海深H，即可直接拟合出单参数F。

1.2 舰船噪声特性研究

舰船在航行中，所产生的辐射噪声可以分为三大类：机械噪声、水动力噪声和螺旋桨噪声。机械噪声主要由舰船上的各种机械振动所产生，其中的线谱部分主要是各种部件产生的振动基频及其谐波分量，而连续谱噪声主要来自于各种管道中流体的空化以及轴承的机械摩擦等。螺旋桨噪声，是由螺旋桨旋转所带来的噪声。当螺旋桨在水中的旋转频率达到一定阈值时，其在叶片表面产生的负压区会出现空化，气泡破裂时产生的空化噪声是连续谱。另外一种称为“唱音”的螺旋桨噪声则是由螺旋桨叶片切割水流引起叶片共振而产生的，其与螺旋桨转速直接有关，且满足一定关系：

其中：n是螺旋桨叶片数；m是谐波次数；s是螺旋桨转数。其在频谱上的贡献主要是线谱以及部分连续谱。水动力噪声则主要由水介质流过舰船表面所产生，其成因非常多，但在舰船正常航行过程中对频谱的贡献较小，往往被机械噪声和螺旋桨噪声所掩盖[14]。

三类辐射噪声有不同的产生机理，在不同的航速和工况下，每一类对舰船辐射总噪声的贡献也不同。在稳定的正常航速时，舰船噪声主要由机械噪声和螺旋桨噪声贡献，其频谱主要分布于 10～2 000 Hz范围，而此范围也在单参数模型的适用范围内。且舰船噪声为宽带连续信号，其连续性有利于对连续时间内变化的传播损失进行研究，其宽带特征有利于反演得到多个不同频率的海底单参数。因此将舰船噪声作为声源进行地声反演具有研究价值。

1.3 舰船噪声反演海底单参数

用宽带连续声源进行水下声传播实验，相比定点发射声源（如脉冲声）具有更宽的频谱，能获得更丰富的声场信息。

由于单参数FdB对于频率较敏感，因此对于不同频率的单参数分别进行反演。基于单参数模型[11]可以得到声源声强I0在距离r处的浅海平均平滑场强I的表达式：

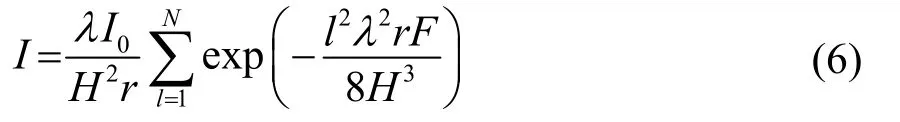
其中，有效简正波波数N=2H/λ，由此可以计算得出传播损失LTC。在N个不同距离ri上计算得到传播损失LTC（ri）与实际测量得到的声传播损失LT（ri）之差的绝对值为 ΔLT（ri），在不同距离上的 ΔLT（ri）的平均值为，定义ΔLT（r）的标准差作为代价函数：

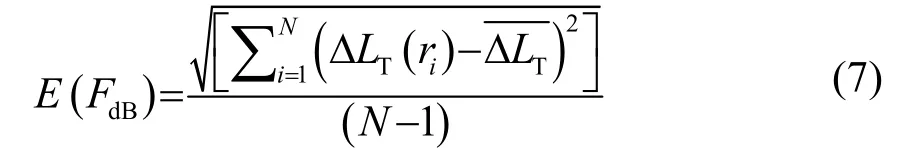
利用式（3）对FdB和F进行转换，代价函数中选用FdB，通过穷举法搜索FdB的值，使代价函数最小的FdB即为反演值。穷举法搜索FdB时，搜索范围为0.01～40。

2 实验研究

2.1 反演过程

实验数据来自某浅海海域的声源传播实验。实验海域的海深为65 m，地势较为平坦，其声速剖面由温盐深仪测得，如图2所示，剖面为正梯度声速剖面。实验采用的8阵元水听器阵，内置20 dB放大器，其工作频带为 20 Hz～20 kHz。由于水听器阵受海流影响易发生倾斜，在水听器阵首尾分别固定一个温深仪，来计算阵列的倾斜角度。水听器阵位于图3中的G点，实验船以稳定的9节航速沿图中FH航行，因此利用水听器接收到的噪声数据得到噪声级，结合实验船的声源级，二者之差即为该海域不同距离的传播损失实测值。实验数据选取垂直阵中 21m 处的水听器，水听器的灵敏度为-169dBV/（1μPa）。

舰船相对水听器的空间位置随时间在不断变化。图4给出了实验船通过水听器附近时的时频图。从图4可以看出，频率在250 Hz以下时噪声的强度随时间并没有太多变化，而在300～1 500 Hz范围内，从图中0～300 s能观察到有舰船通过的“U”型拐点。图5是有实验船通过与无实验船通过时的海洋环境噪声功率谱密度对比。从图5中能更直观地看出在300～1 500 Hz范围内的船噪声比较高。

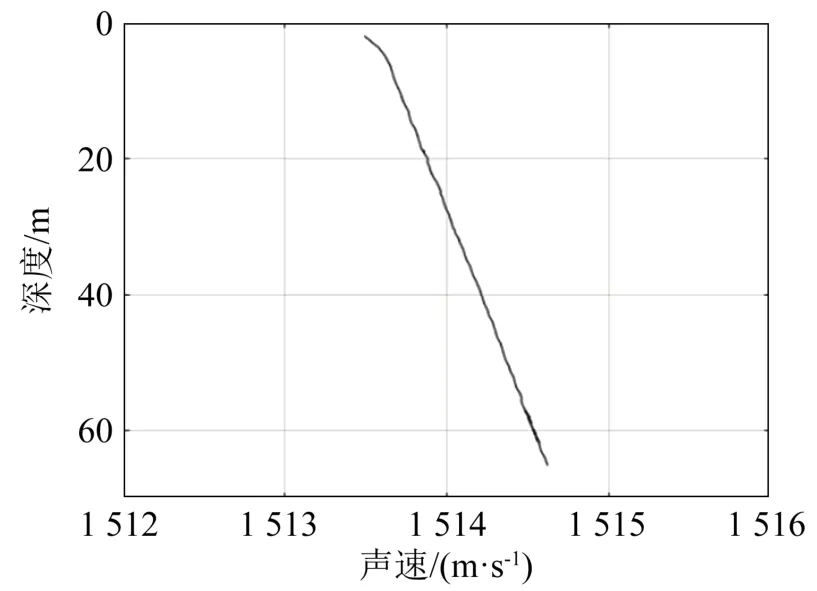
图2 实验海域声速剖面Fig.2 Sound speed profile in experimental sea area

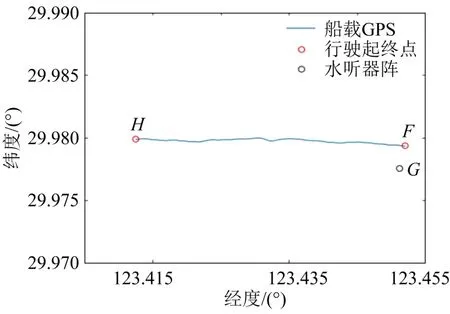
图3 实验船航迹Fig.3 The track of experimental ship

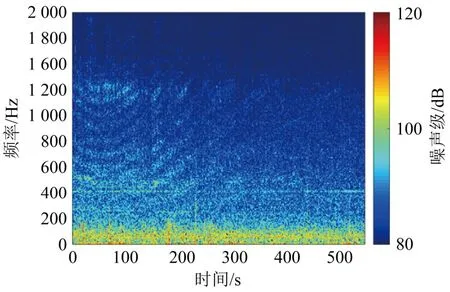
图4 实验船噪声的时频图Fig.4 Spectrogram of experimental ship noise

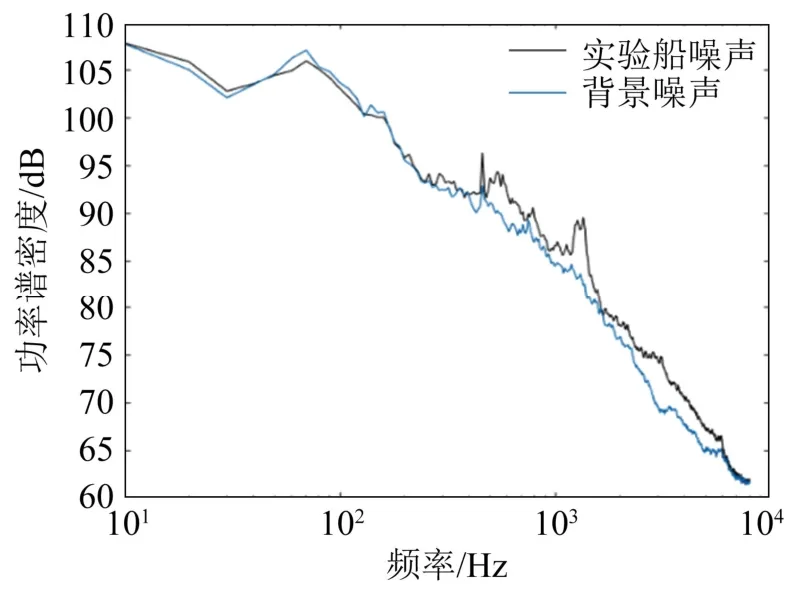
图5 实验船噪声与背景噪声功率谱密度Fig.5 Power spectral densities of experimental ship noise and background noise

实验选取舰船距离水听器 900～2 500 m 内的数据进行反演，将每2 s的数据作为一个样本，窗函数选择汉宁（Hanning）窗，重叠率为50%。将数据共分成M组，对315、400、500、630 Hz海底单参数进行反演，实验数据均经过1/3倍频程处理。

图6～9分别为利用实验船噪声所得的 315、400、500、630 Hz的传播损失和代价函数随单参数变化的曲线。图6（a）、7（a）、8（a）、9（a）均为实验得到的实测传播损失，将其与通过式（6）计算得到的计算传播损失一并代入式（7）中可以得到代价函数随单参数FdB变化的曲线（图6（b）、7（b）、8（b）、9（b））。通过穷举法可以找到使得代价函数最小时的单参数FdB，即为反演所求的单参数。

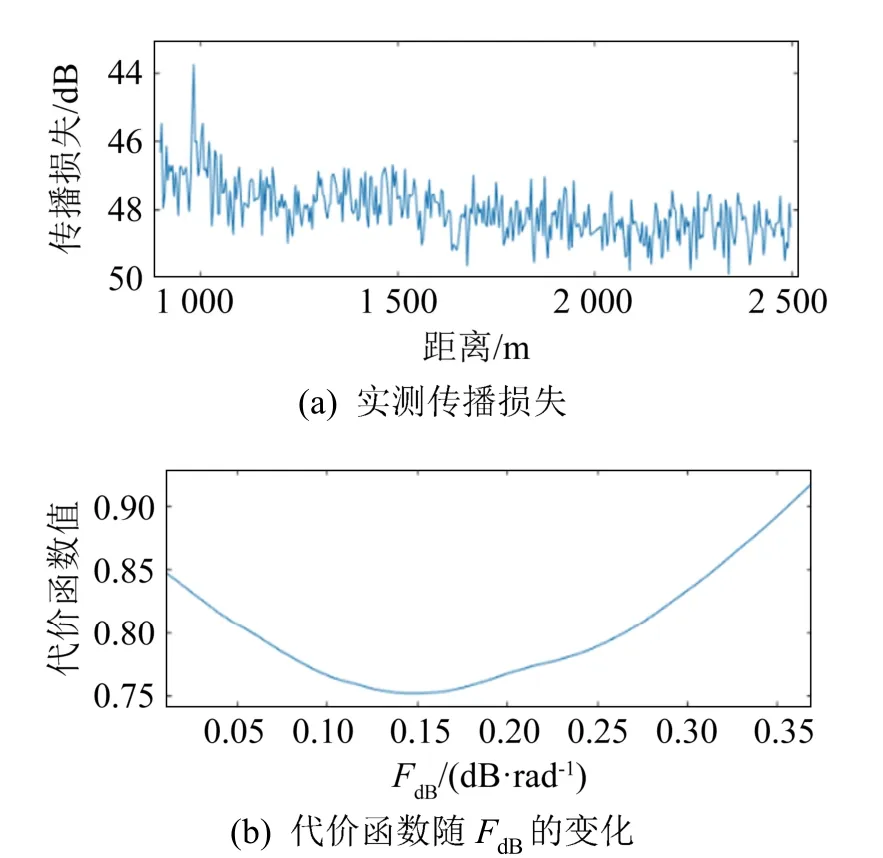
图6 实验海域传播损失与代价函数随单参数FdB的变化（315 Hz）Fig.6 Transmission loss in experimental sea area and the variation of cost function with the single parameterFdB(315 Hz)

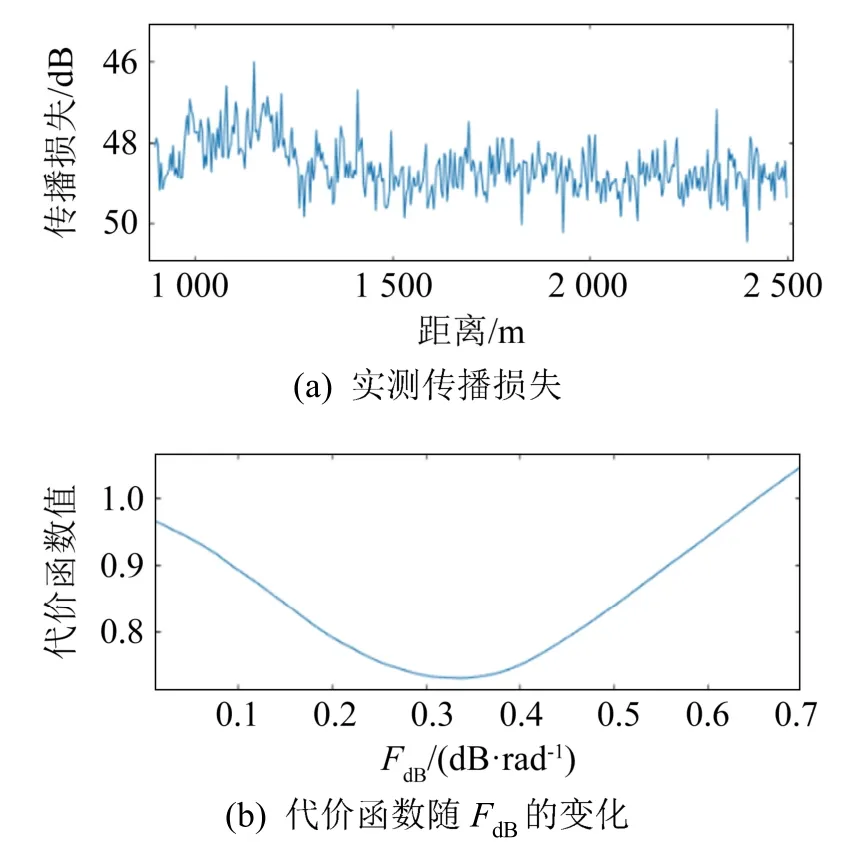
图7 实验海域传播损失与代价函数随单参数FdB的变化（400 Hz）Fig.7 Transmission loss in experimental sea area and the variation of cost function with the single parameterFdB(400 Hz)

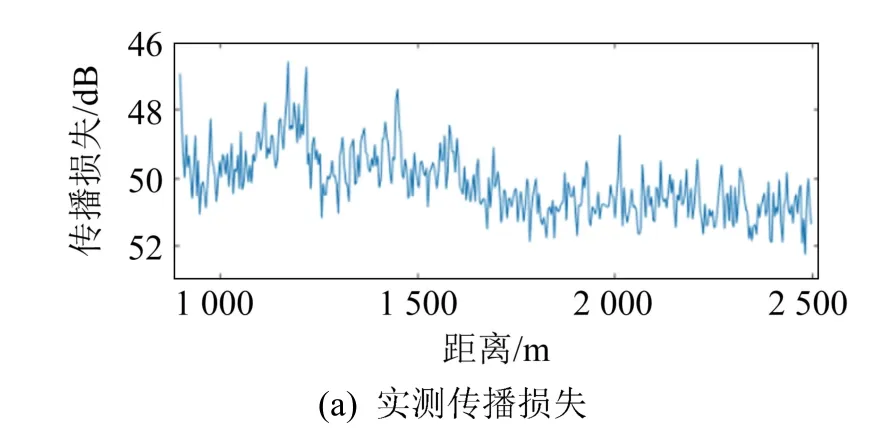
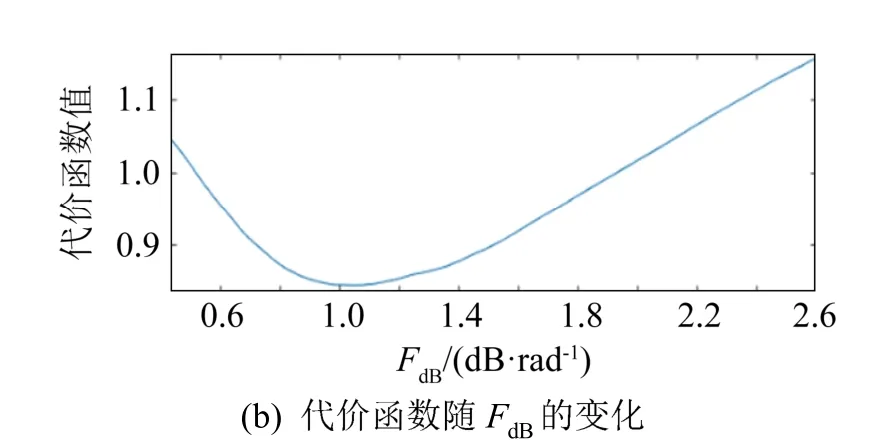
图8 实验海域传播损失与代价函数随单参数FdB的变化（500 Hz）Fig.8 Transmission loss in experimental sea area and the variation of cost function with the single parameterFdB(500 Hz)

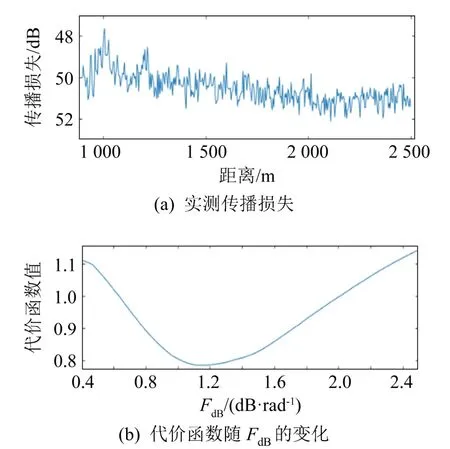
图9 实验海域传播损失与代价函数随单参数FdB的变化（630 Hz）Fig.9 Transmission loss in experimental sea area and the variation of cost function with the single parameterFdB(630 Hz)

2.2 反演结果及分析

在900～2 500 m距离范围内反演315、400、500、630 Hz的单参数FdB，具体频率对应的单参数值如表1所示。

表1 单参数FdB的反演结果Table 1 Inversion results of single parameterFdB

结合表1各频率的海底单参数值可以拟合得到海底单参数与频率的关系曲线如图10所示。二者的非线性关系为FdB=3 .39·f2.16，其中f的单位为kHz。

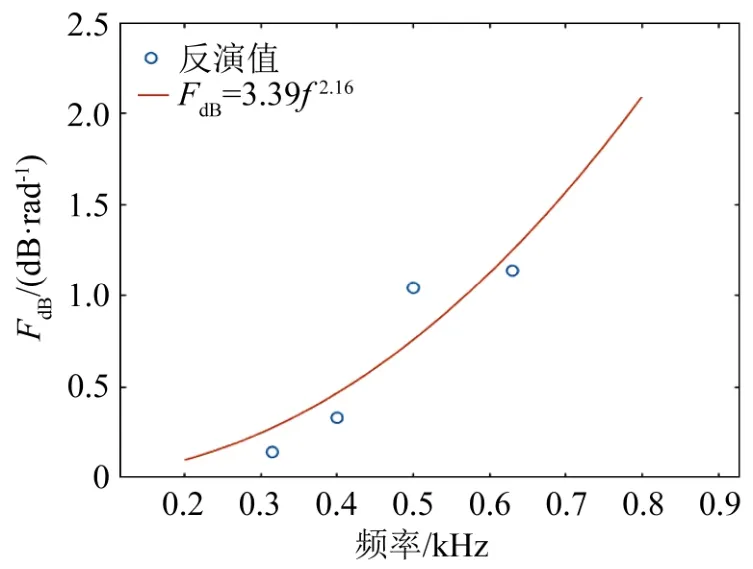
图10 单参数FdB随频率变化的拟合曲线Fig.10 Fitting curve of single parameterFdBvs. frequency

为了验证反演结果，图11～14分别给出了315、400、500、630 Hz信号利用单参数反演结果预报的传播损失与实测值的对比。从图11～14中可以看出，4张图中的预报曲线与实测值吻合程度较好，验证了反演方法的有效性。因此，可以在该方案基础上进一步开展后续研究。

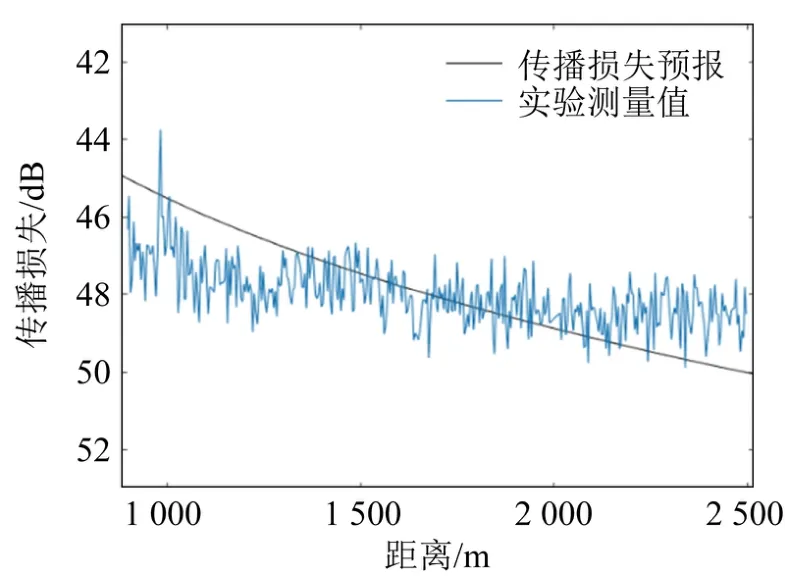
图11 315 Hz时传播损失预报与测量值Fig.11 Comparison between predicted and measured transmission loss values at 315 Hz

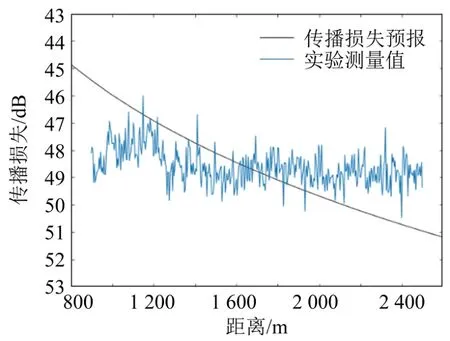
图12 400 Hz时传播损失预报与测量值Fig.12 Comparison between predicted and measured transmission loss values at 400 Hz

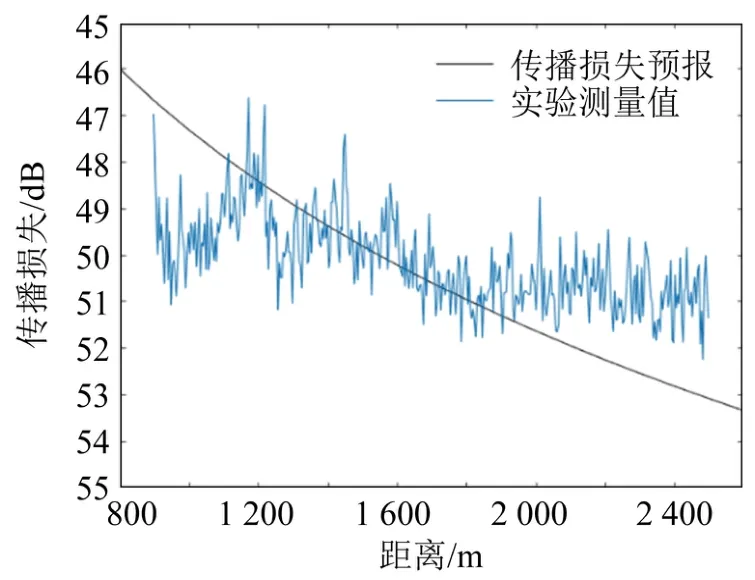
图13 500 Hz时传播损失预报与测量值Fig.13 Comparison between predicted and measured transmission loss values at 500 Hz

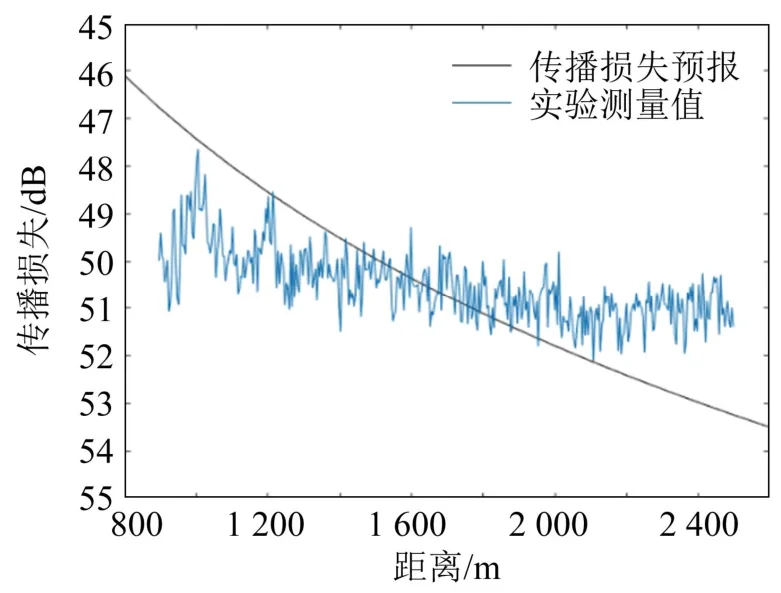
图14 630 Hz时传播损失预报与测量值Fig.14 Comparison between predicted and measured transmission loss values at 630 Hz

3 结 论

利用舰船噪声反演海底底质往往需要多维参数模型，复杂度高，计算时间长。因此，提出一种使用舰船噪声作为声源的海底单参数反演方法，通过设计代价函数，仅需要一维寻优即可得到海底单参数。相较之基于主动声源的海底单参数反演，利用舰船噪声作为声源虽然有部分不足，如信号强度较低，反演存在误差、需要先获得舰船噪声声源级等。但在实际航行中依然具有声源易获取、信号频带宽等优势。

结合在某海域进行的声传播实验数据，对该海域的海底单参数进行了反演，并对单参数与频率的关系进行了拟合分析，得到了较为一致的结果。利用单参数预报的传播损失与实际测量值也有比较好的吻合效果。