基于差值迭代法的矮塔斜拉桥施工索力计算和影响因素研究

李月富 张清旭 宁晓骏 杨东

(1.昆明理工大学建筑工程学院 昆明 650500； 2.江苏省南通外向型农业综合开发区管理委员会 江苏南通 226400)

0 引言

20世纪90年代末以来，我国已建成100余座矮塔斜拉桥，该类桥是一种使用斜拉索辅助主梁受力，结合了混凝土梁桥“刚”和常规斜拉桥“柔”的新型桥梁，其斜拉索也被称为体外预应力，可根据实际情况灵活布置[1]。斜拉索的竖向分力可减小梁体的竖向弯矩和下挠，同时水平分力产生的偏心弯矩可提供体外预应力，使整桥形成高次超静定结构[2]。然而，斜拉索张拉施工会使桥梁发生体系转换，施工索力的偏差不仅影响结构的内力分布，还严重威胁施工和成桥阶段的安全。因此，确定施工索力是斜拉桥施工控制的关键，不仅要确保每个施工阶段的安全，还要使施工完成的索力满足设计的成桥要求[3]。

同时，由于矮塔斜拉桥是高次超静定结构，其索力受多种因素影响[4]。在实际施工中，混凝土容重、混凝土弹性模量等由于客观原因，不可避免地会出现改变或偏差，各参数的变化对结构内力和安全性的影响不容忽视[5]。基于此，本文以某矮塔斜拉桥为背景，基于差值迭代法对施工索力进行优化，并选取了施工中容易发生改变的主梁混凝土容重、混凝土弹性模量、预应力筋张拉应力3个状态参数进行分析，探索各参数对索力影响的敏感性。

1 工程背景

某大跨径矮塔斜拉桥的跨径布置为(99+180+99) m，桥宽为25.8 m，桥型布置如图1所示。主梁截面为变高单箱三室全预应力混凝土箱梁，梁底纵向为二次抛物线，梁高由索塔根部5.8 m变化至端部3 m。索塔为高29 m的矩形实心断面钢筋混凝土结构，布置在中央分隔带上。斜拉索为单索面双排索，索塔每侧9对斜拉索，全桥共36对，每对索横向间距为1 m。斜拉索编号规则为：索塔向边跨方向依次编为1～9号，索塔向跨中方向依次编为10～18号。索塔、主梁和桥墩固结连接，各构件材料特性参数如表1所示。

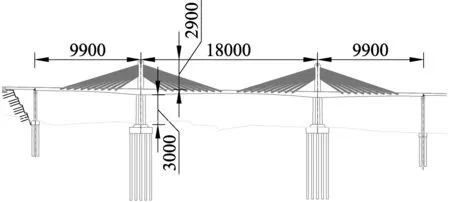
图1 桥型立面布置(单位：cm)

表1 材料特性参数

2 建模和施工步骤

运用桥梁有限元分析软件Midas/Civil 2020进行建模分析，结构模型如图2所示。使用梁单元模拟主梁、桥墩和索塔等杆性构件，斜拉索采用只受拉单元模拟，全桥共343个节点和302个单元，斜拉索的张拉过程通过向受拉单元赋予初拉力的方式模拟。施加荷载有结构自重、预应力荷载、斜拉索张拉力、施工荷载、二期桥面铺装荷载等。

图2 有限元模型

施工索力计算受施工过程模拟的影响较大，因此要尽可能准确、合理地模拟每个施工阶段。根据实际施工过程，主梁分为2个T构独立施工。第一次转换体系时，与边跨现浇段进行合龙，T构由静定结构转换成一次超静定结构；第二次转换体系时，完成跨中合龙，结构由低次超静定结构转换成高次超静定结构，两部分连为一个整体。因此，模拟的主要施工步骤如表2所示。

表2 主要施工步骤

3 合理施工索力求解

3.1 差值迭代法步骤

背景桥梁的所有斜拉索均为一次性张拉施工完成，因此选用精度较高、收敛速度快的差值迭代法计算施工索力。该方法综合考虑所有拉索对结构的影响，适用于一次性求出全部索力的情况[6]，主要步骤如下：首先赋予一组初次张拉力T0，按照已拟定的施工步骤进行正装计算，直到最后一个施工阶段完成，获得初次施工索力F0。而F0与设计的成桥目标索力F之间存在一个差值：

△F0=F0-F

(1)

为消除这一差值，取第二组张拉力T1：

T1=T0-△F0

(2)

代入计算得到第二组成桥索力F1，F1与成桥目标索力F之间的差值为：

△F1=F1-F

(3)

重复上述步骤迭代计算，不断缩小施工索力Fi与成桥目标索力F之间的差值为：

△Fi=Fi-F

(4)

最终，计算精度p需要满足要求：

(5)

3.2 迭代计算过程

由于本桥是对称结构，则左右两个半跨的索力相等，因此只需对一个半跨拉索进行求解。为加快迭代的收敛速度，根据工程经验，现使第一组张拉力T0等于成桥目标索力F进行正装计算，成桥目标索力如表3所示。经过4次迭代满足精度要求，迭代过程中的索力和特征值变化分别如图3和表4所示。可以看出，随着迭代次数的增加，施工索力不断接近成桥目标索力，△F和p值不断减小，短索的收敛速度比长索的快，这是由斜拉桥的索力分布规律所决定的，即斜拉索越长的索力越大。前2次迭代达不到精度要求，第三次迭代p=1.41%<2%，虽满足要求，但施工索力与目标索力仍有较大差值，精确度有待提高，故进行第四次迭代。

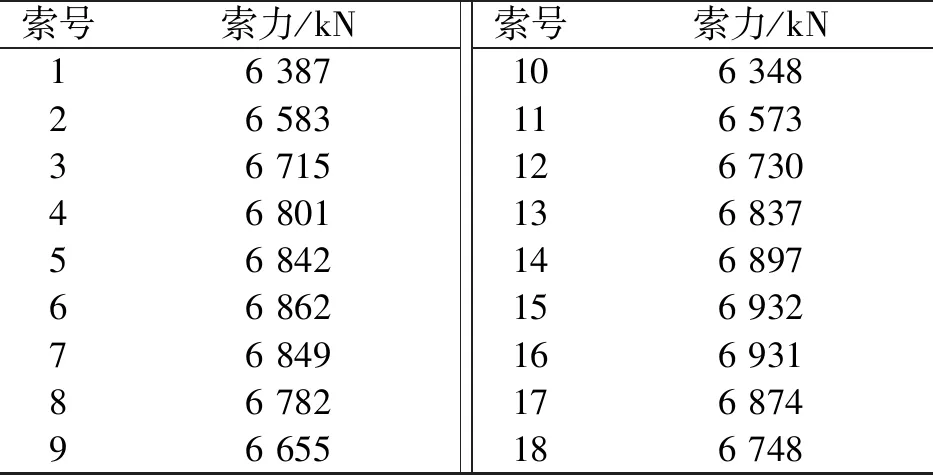
表3 成桥目标索力

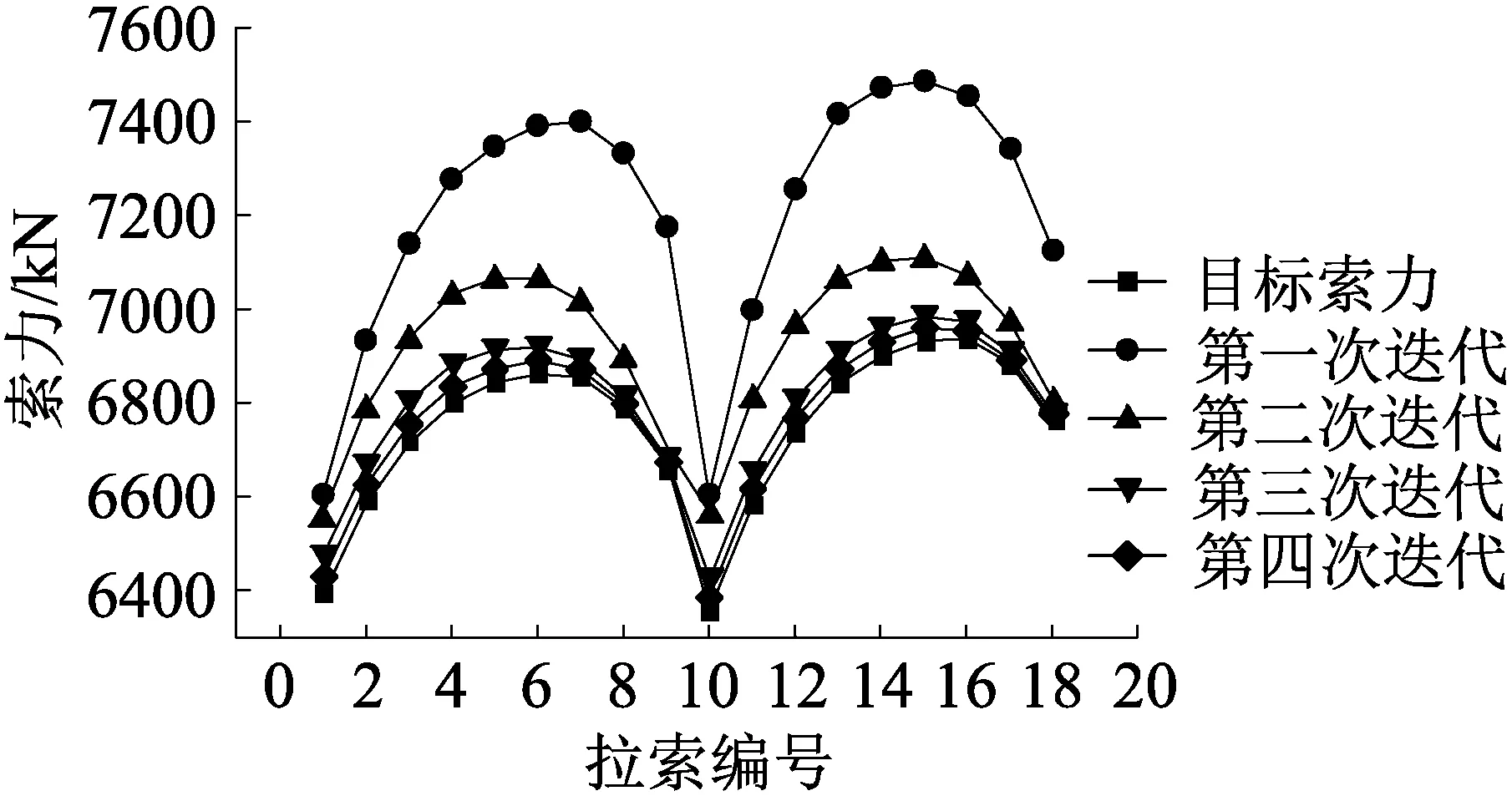
图3 索力迭代变化过程

表4 迭代过程中各特征值

经过第四次迭代，p=0.35%满足精度要求，△F最小值为5 kN，△F最大值为24 kN，与第一次迭代相比，差距缩小了94.7%，获得的索力值非常接近目标索力，因此可认为迭代完成，按第四次迭代结果取值。

3.3 施工索力验算

为验证所求施工索力是否合理，同时考虑施工荷载、温度、预应力和混凝土湿重等荷载，将第四次迭代获得的施工索力带入全桥模型，进行整桥施工阶段分析，以最终成桥阶段的主梁弯矩、位移和应力为检验指标[7]，分别如图4～图6所示。

图4 成桥阶段主梁弯矩

图5 成桥阶段主梁位移

图6 成桥阶段主梁应力

由图4～图6可知，成桥阶段主梁最大负弯矩为-9.5×105kN·m，出现在桥塔附近无索区部位；最大正弯矩为8.6×104kN·m，出现在跨中附近；最大挠度为20.1 cm，出现在跨中附近；最大压应力为12.2 MPa，出现在主塔周围；最大拉应力为0.89 MPa，出现在边跨现浇段旁边。各项力学指标均满足《公路斜拉桥设计规范》(JTG/T 3365-01—2020)的要求，远小于容许值，验证了所求施工索力的合理性和精确性。

4 状态参数对索力的影响

状态参数偏差是桥梁施工中产生结构误差的重要原因之一，不同状态参数变化对同一构件的影响程度也不一致。状态参数包括环境温度、湿度、材料容重、弹性模量、斜拉索和预应力钢束的张拉控制应力等[8]。在实际施工中，状态参数经常由于施工环境、材料、施工误差等客观原因发生改变，因此在施工控制中要重点关注主要影响因素。根据本桥的实际情况和工程经验，以合龙前最大双悬臂状态为基准，选取主梁的混凝土容重、混凝土弹性模量、预应力筋张拉应力进行敏感性分析，研究各状态参数对索力的影响程度。

4.1 混凝土容重的影响

对于矮塔斜拉桥而言，主梁一般是混凝土结构，其质量远大于同跨径使用钢箱梁的常规斜拉桥。因此，主梁混凝土容重的大小决定着主梁恒载，会影响桥梁弯矩、挠度等，进而改变斜拉索的索力及其分布[9]。现将混凝土容重按5%的幅度增大和减小，改变情况如表5所示，其对斜拉索索力的影响如图7所示。可以看出，混凝土容重从0.9γ变化至1.1γ时，边跨和主跨的斜拉索索力均随容重的增加而变大，由于恒载随容重增大，索力也随之增加。增幅在2～5号拉索时保持基本平稳，6～9号拉索增幅逐渐减小，边跨和主跨拉索索力变化呈对称趋势。容重增加10%时整体索力最大，相比设计索力最大增值为215.99 kN；容重减小10%时整体索力最小，最大减小值为216.02 kN。

表5 主梁混凝土容重γ变化值 单位：kN/m3

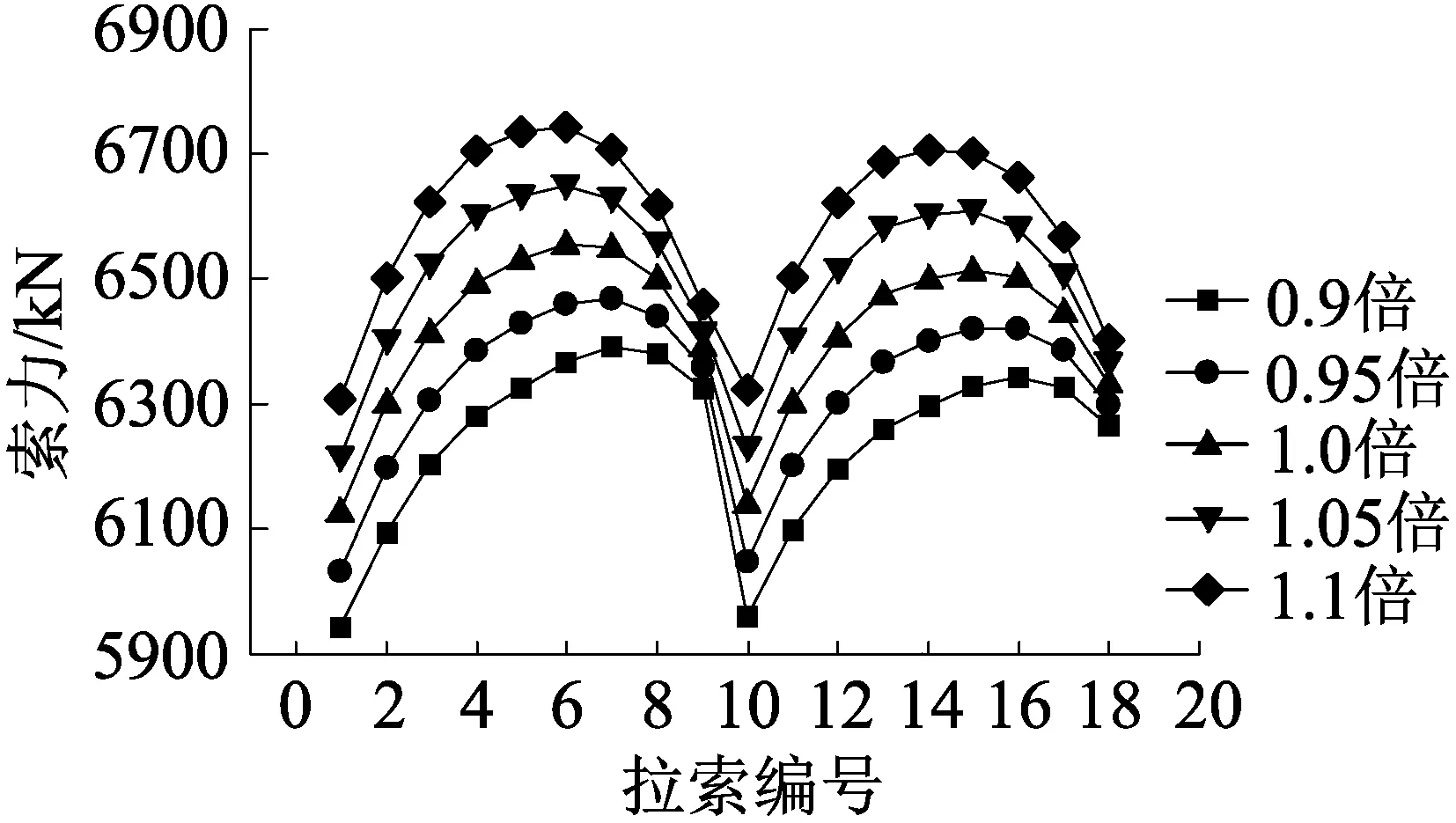
图7 混凝土容重改变对索力的影响

4.2 混凝土弹性模量的影响

矮塔斜拉桥具有“刚柔并济”的特点，其主梁的刚性主要取决于混凝土弹性模量。为探究主梁混凝土弹性模量对索力的影响，将其按5%的幅度改变大小，如表6所示，其影响结果分析如图8所示。可以看出，混凝土弹性模量由0.9E变化至1.1E时，边跨和主跨的索力随弹性模量的增加而减小，这是由于随着弹性模量的增加，主梁刚度提高，结构达到平衡时需要的索力随之降低。弹性模量增加10%时索力最小，相比设计索力最大减小值为66.03 kN；弹性模量减小10%时索力最大，最大增加值为65.90 kN。

表6 主梁混凝土弹性模量E变化值 单位：GPa

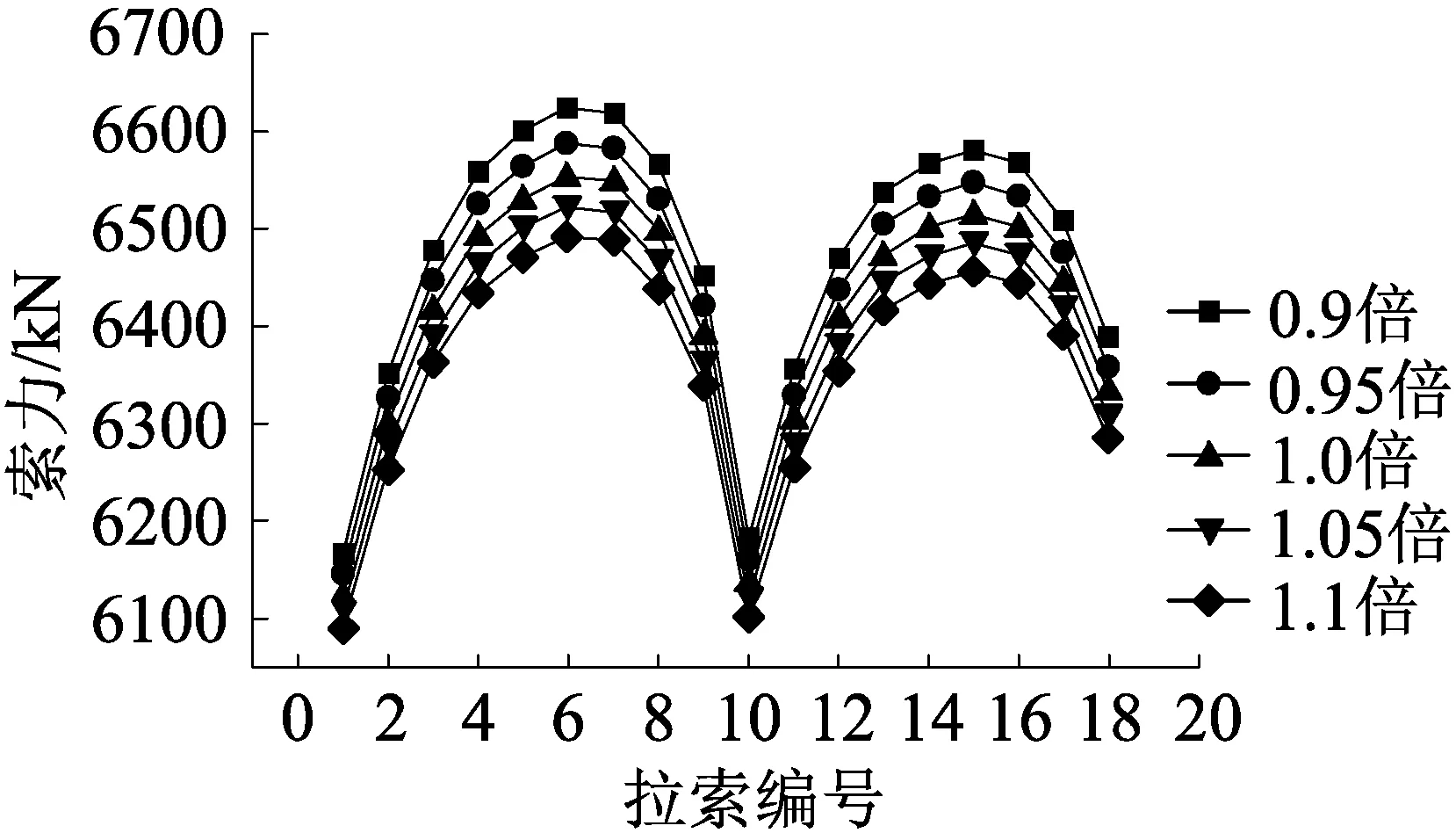
图8 混凝土弹性模量改变对索力的影响

4.3 预应力筋张拉应力的影响

对主梁施加预应力能有效降低较大的跨中弯矩和挠度，改善主梁截面的应力状况，减小混凝土开裂的几率。对于矮塔斜拉桥，斜拉索可作为体外预应力，与主梁内的预应力协同工作，具有较好的受力改善效果[10]。但在施工过程中，经常因张拉设备、测量误差等造成张拉应力偏低或偏高。为探究预应力筋张拉应力偏差对斜拉索索力的影响，将张拉应力fp按照5%的幅度增减，如表7所示，分析其对斜拉索索力的影响如图9所示。可以发现，预应力筋张拉应力从0.9fp变化至1.1fp时，两侧斜拉索索力均随张拉应力的增加而减小，变化幅度前6号拉索基本平稳，7号拉索之后逐渐变小，边主跨拉索索力变化呈对称趋势。预应力筋张拉应力增加10%时索力最小，相比设计值最大减小值为136.69 kN；预应力筋张拉应力减小10%时索力最大，最大增加值为136.35 kN。这是由于主梁体内预应力与斜拉索形成的体外预应力协同互补工作，因而两者成反比。

表7 预应力张拉应力fp变化值 单位：MPa

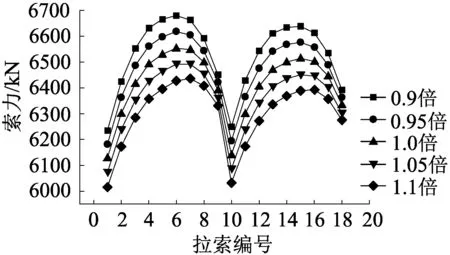
图9 预应力筋张拉应力改变对索力的影响

4.4 各参数敏感性分析

为比较上述3个状态参数对索力的影响程度，确定主次影响因素，需要对控制目标受各参数的影响程度进行敏感性分析。因此，将控制目标斜拉索索力设定为变量y，将敏感性分析的参数设定为x，其变化值为△x，则结构的目标状态和参数之间存在如下函数关系[11]：

y=f(x)

(6)

令x0为x的原始状态参数，由于状态参数的变化幅度为5%，则：

y1=f(x0+△x)=f(1.05x0)

(7)

y2=f(x0-△x)=f(0.95x0)

(8)

定义参数敏感性目标值为q，则：

q1=|y1-y0|=|f(1.05x0)-f(x0)|

(9)

q2=|y2-y0|=|f(0.95x0)-f(x0)|

(10)

故q值越大，控制目标对于该参数敏感性越强。为综合比较各参数的变化对于控制目标值的影响，结合归一化的处理思路，并定义影响系数α：

(11)

式中，qmax、qmin分别为控制目标值在各参数影响下的最大值、最小值。

参照文献[12]，影响系数α的控制阈值为0.3，当α>0.3时视为主要影响因素，当α<0.3时视为次要影响因素，计算结果如表8所示。可以发现，以斜拉索的索力为控制目标，参数敏感性由强至弱依次为：混凝土容重、预应力筋张拉应力、混凝土弹性模量。进行归一化处理后，混凝土容重的影响系数大于0.3，是主要影响因素，预应力筋张拉应力和混凝土弹性模量影响系数小于0.3，是次要影响因素。因此，施工中需重点关注主梁混凝土容重。

表8 斜拉索内力参数敏感计算

5 结论

本文以某矮塔斜拉桥为工程背景，运用差值迭代法进行施工索力优化计算，并分析了主梁混凝土容重、混凝土弹性模量、预应力筋张拉应力变化对斜拉索索力的影响敏感性，得到如下结论：

(1)差值迭代法适用于施工过程中拉索一次性张拉到位的情况，可同时考虑所有拉索对结构的影响。以索力为控制目标进行正装分析，可综合考虑桥梁成桥过程中的收缩徐变效应和结构非线性等影响因素，该方法适用于类似矮塔斜拉桥的施工索力计算。

(2)本文共使用4次差值迭代获得了矮塔斜拉桥的合理施工索力，精确度p=0.35%，迭代过程中短索的收敛速度快于长索。把计算的索力带入到原桥施工分析，成桥阶段的主梁弯矩、位移和应力均满足规范要求，验证了所求施工索力的合理性，同时证明了差值迭代法精度高、收敛速度快的优势。

(3)全桥斜拉索索力随主梁混凝土容重的增加而增大，随混凝土弹性模量和预应力筋张拉应力的增大而减小。以斜拉索索力为控制目标，参数敏感性由强到弱的顺序为：混凝土容重、预应力筋张拉应力、混凝土弹性模量。经归一化分析发现，混凝土容重是主要影响因素，后两者为次要影响因素。容重大小决定了恒载大小，因此在施工过程中要重点控制主梁混凝土容重，避免其发生变化影响索力值。