列车端部双层方管组合式吸能结构耐撞性研究

高广军，谭易成，于尧

(中南大学 交通运输工程学院，湖南 长沙 410075)

迄今为止，碰撞仍然是列车面临的主要事故风险之一，其引起的交通事故给人类的生命和财产带来极大的威胁和伤害[1-2]。2019年2月8日，西班牙东北部城市巴塞罗那近郊发生一起2列火车相撞事故，造成至少1人死亡、95人受伤。因此，如何将列车车体结构耐撞性提升在当今社会非常重要，而安装于列车端部吸能结构[3-4]的耐撞性与列车车体结构耐撞性密切相关，因此，需要对列车吸能结构不断研发和升级。在过去几十年中，国内外对各种薄壁结构的吸能性能进行了大量的研究。ABRAMOWICZ等[5]通过运动学的分析方法研究了方管的轴向渐进压溃，并且根据不同管边长和高度的比值预测了4种变形模式。WANG等[6]以方管和铆钉为载体，提出了刚度可控性设计方法，建立了基体结构与增强部件之间的匹配关系，研究了通过铆钉增强局部刚度对方管在轴向冲击载荷下的变形模式的影响。GAO等[7]研究了带隔板的薄壁方管在轴向冲击载荷下的耐撞性，得出隔板可提高方管变形稳定性。但此种吸能结构压缩力仅由单一薄壁管提供，在壁厚较小时可能会存在压缩力不足的情况。ALI等[8]从理论、仿真和试验等方面对截面为五边形和十字形的薄壁管吸能特性进行了研究，得到在相同的管壁面积情况下，两者吸能量比矩形管高出31%～60%和48%～92%。FAN等[9]对具有不同横截面的薄壁金属管，六边形、八边形、12边和16边星形进行了准静态轴向载荷下的能量吸收能力研究，发现直径与厚度比值小于50时，12边星形具有最佳的能量吸收能力。但是这种方案在应用中也存在以下问题：在作为承载式吸能结构时，吸能结构位于列车车体底架纵向方向的两端，并与底架其他部分结构组焊起来形成完整的车体底架结构。相对于方管和矩形管来说，无论是五边形、六边形、八边形、十字形或是12边星形，均会大大增大加工和安装的难度。YU等[10]提出了一种具有大压缩行程的新型吸能装置，该装置由吸能蜂窝铝结构、卷形金属吸能板、导向轮以及支撑装置构成，其能够产生比其自由长度大得多的变形行程。但此吸能结构存在压缩力较小的问题。目前高速列车以及城轨列车车钩压溃管大多采用了鼓胀管吸能结构[11]。但鼓胀管同样存在压缩率较低，轴向尺寸较大的缺点。本文提出了一种具有内外方管的组合式吸能结构，其压缩率仅受到单个方管壁厚的影响，因此压缩率比较高，同时其压缩力由内外方管共同形成，因此压缩力比较大。为了提高方管褶皱的量数，内外方管之间通过横向隔板连接，使得吸能结构在每2个隔板中间产生稳定的变形。同时在方管侧壁开有诱导槽。相对于带隔板的普通方管，其充分利用了方管的内部空间，并提升了轴向载荷下的吸能特性。在同等几何尺寸时，其相对于圆管[12]吸能量高，变形模式稳定，相对于蜂窝式结构[13]加工工艺简单，成本低。图1显示了在城轨列车头车中作为主吸能结构安装于承载式底架的组合式吸能结构使用示例。

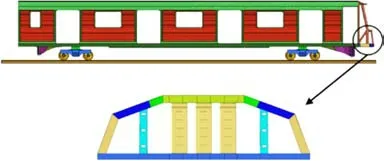
图1 列车端部双层方管组合式吸能结构Fig.1 Double layer square tube combined energy absorbing structure as energy absorbers

1 几何模型

本文中的吸能结构是具有方形截面，带有隔板的薄壁管。整个试件均由20钢材料制作而成，此种材料属于含碳量为0.2%的低碳钢，该钢韧性、塑性和焊接性均好。吸能结构几何模型如图2所示。

如图2(a)所示，外管截面为210 mm×210 mm，内管截面为120 mm×120 mm。内管置于外管之中，两者具有相同的中心线，长度均为660 mm，皆厚3 mm。方管是由2片弯曲成U形的20钢钢板焊接而成，圆角半径均为10 mm。方管的两端都由刚性端板封闭，两端的刚性平板为正方形，边长为400 mm，厚度为15 mm。隔板的几何尺寸如图2(b)，它连接着内管与外管，沿着长度方向均匀分布在2个管之间，隔板的厚度为4 mm，隔板与隔板之间的间隔是110 mm。隔板能够增大方管的横向强度，约束屈曲模式，使方管依次发生渐进屈曲，从而提高能量吸收能力。在靠近撞击端的方管两侧管壁上，第1个隔板与端板底部的中间部分开了诱导槽，外管诱导槽的宽度为16 mm，深度为4 mm，内管诱导槽的宽度为12 mm，深度为3 mm，诱导槽均贯穿方管两侧上端面。该结构可有效降低结构初始撞击力峰值，同时诱导结构在冲击端率先产生屈曲变形。整个试件的三维图如图2(c)所示。

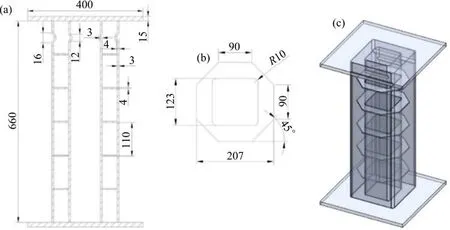
图2 吸能结构几何模型Fig.2 Geometric model

2 有限元数值仿真试验

2.1 有限元模型

采用LS-DYNA软件对双层方管组合式吸能结构进行有限元仿真分析。建立的有限元模型包含以下几个组件：外管、内管、隔板和端板，如图3所示。为了模拟实际接触，准确观察管的变形过程，选用壳单元模拟吸能器。LS-DYNA是一个典型的显式有限元软件，其时间步长受最小网格尺寸的影响。由于有限元法是基于结构的网格离散化，结构的网格划分对仿真结果的正确性有很大的影响。一般来说，较小的网格尺寸可以得到更准确的结果。因此，在模拟结构变形时，应选择合适的网格尺寸进行网格划分，吸能器网格尺寸为3 mm×3 mm。双层方管组合式吸能结构有限元模型网格数目为141 876。吸能结构的端板与试验台车的接触被定义为“TIED_NODE_TO_SUR‐FACE”接触。吸能结构在变形过程中自身的接触被定义为“AUTOMATIC_SINGLE_SURFACE”接触。吸能结构在试验台车上的安装位置如图4所示，通过能量换算得到在冲击速度为 4.2 m/s情况下吸能结构在有限元数值仿真试验中压溃完全，故定义试验台车的初始速度4.2 m/s，竖直方向重力加速度g为9.81 m/s2。试验台车和吸能结构有限元模型总质量为26.17 t。在吸能结构前端建立刚性墙。LI等[14]已经对20钢材料进行了详细的材料拉伸试验，Johnson-Cook材料本构模型可以有效模拟低碳金属钢材的弹塑性变形，将已有材料试验获得的弹塑性材料参数导入该材料本构模型中，从而准确模拟吸能结构的压溃屈曲变形。表1列出了20钢的材料参数。

表1 吸能结构的材料参数Table 1 Material parametersof energy absorbing structure

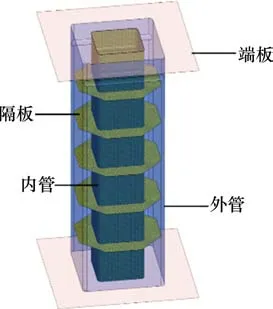
图3 吸能结构有限元模型Fig.3 Finite element model of energy absorbing structure

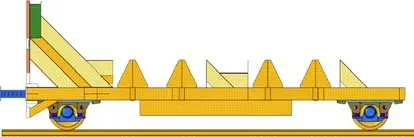
图4 吸能结构在试验台车上的安装位置Fig.4 Relative position of energy absorber and test sled

2.2 仿真结果

仿真变形模式结果如图5所示。屈曲变形率先在诱导槽附近产生，内管和外管均向远离撞击端方向依次发生渐进屈曲，两者均产生6级屈曲变形。每2块隔板之间形成1个褶皱，且隔板的变形量很小，起到了很好的约束作用。列车端部双层方管组合式吸能结构仿真过程中撞击力−位移曲线如图6所示。

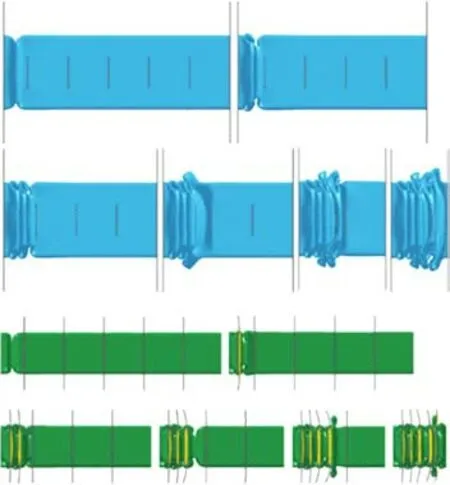
图5 仿真中吸能结构变形模式Fig.5 Deformation process

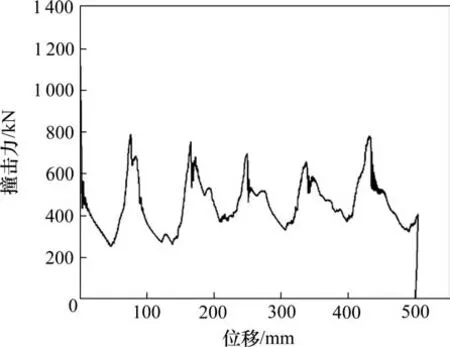
图6 有限元仿真中获得的撞击力-位移曲线Fig.6 Impact force displacement curve obtained in finite element simulation

从图6中可以清楚的发现，吸能结构在撞击刚性墙后撞击力剧增，出现一个明显的初始撞击峰值力。随后随着吸能结构触发变形，撞击力迅速下降，结构进入稳定屈曲变形过程，撞击力趋向规律化，随着褶皱的产生，撞击力457.29 kN左右依次形成波峰、波谷状的起伏变化。随着冲击过程的进行，撞击力逐渐下降至0 kN，此时吸能结构与刚性墙恰好分开。图中曲线与横坐标轴围成区域的面积，即为吸收的能量。

3 吸能装置台车冲击试验

3.1 试验工况及设备布置

于中南大学碰撞台进行双层方管组合式吸能结构台车轴向冲击试验。测试安排包括力传感器、匀力板、测试台车、速度测量仪和高速摄像机。双层方管组合式吸能结构焊接在试验台车前面的安装板上。2个力传感器安装在匀力板和刚性墙之间。在吸能结构重要部位及试验台车不同位置采用标记纸进行标记，便于撞击过程中高速摄影仪的动态捕捉和运动序列图像后处理。高速摄影仪分别放置在侧面和上方，并开启其专用直流光源。带有测试试件的试验台车总重量为26.17 t，冲击速度为4.2 m/s。试验撞击情况如图7所示。

图7 试验撞击工况Fig.7 Impact condition of test

3.2 试验结果与仿真结果对比分析

图8是吸能结构在试验过程中变形模式。通过观察可以发现屈曲变形率先在诱导槽附近产生，并以远离撞击端方向依次发生渐进屈曲。试件一共产生6级屈曲变形，变形过程有序可控，并未发生失稳，屈曲变形较为完整，无撕裂及断裂发生，故前文在材料本构模型中没有考虑失效问题。与仿真结果的变形模式对比分析发现，试验与其在变形模式方面具有一致性。

图8 吸能结构变形模式Fig.8 Crush sequence of specimen in test

双层方管组合式吸能结构最终的压缩位移为501.9 mm。撞击力-时间曲线由2个力传感器的总和给出；位移−时间曲线由高速摄像机采集到数据生成，得到了吸能结构的撞击力−位移曲线。通过轴向动态冲击试验和仿真计算得到的吸能结构撞击力−位移曲线如图9所示。结果表明，两者结果在撞击力−位移曲线上有很好的一致性，具有相同的变化规律。

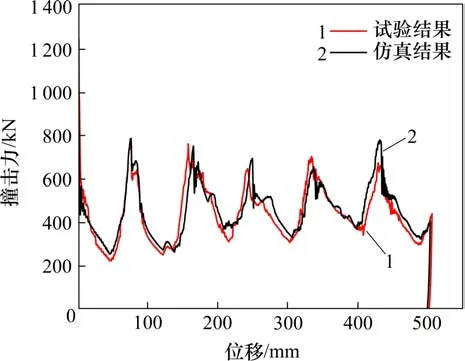
图9 台车冲击试验和有限元仿真中获得的撞击力−位移曲线Fig.9 Comparison of force-displacement curves between simulation and experiment

表2总结了轴向动态冲击试验和有限元模拟之间的耐撞性指标比较。轴向动态冲击试验和有限元模拟的吸能量相对误差为3.22%，平台力相对误差为3.74%。由于相对误差较小，双层方管组合式吸能结构有限元模型的有效性和准确性得以证明。

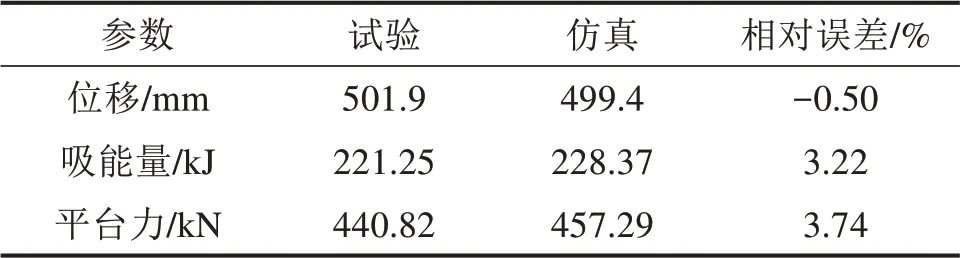
表2 有限元仿真和台车冲击试验结果对比Table 2 Comparison matrix between experiment and simulation

4 不同参数对吸能结构耐撞性影响

4.1 组合式吸能结构与单层吸能结构耐撞性比较

本节将带双层方管组合式吸能结构与带隔板的单层方管耐撞性进行比较。两者外形一致，区别是后者没有内管，仅由外管，隔板与两侧端板组成。图10所示为带隔板的普通方管有限元模型。两者有限元模型底部节点自由度被完全约束。为了缩短计算时间，简化台车有限元模型，定义“RIGIDWALL_PLANAR_MOVING”刚性墙，摩擦因数取0.3。根据EN 15227地铁车辆碰撞标准，刚性墙的速度定为25 km/h[15]，其位置以及速度方向如图11所示。

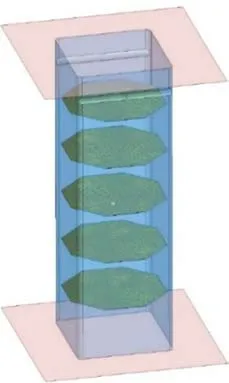
图10 单层方管有限元模型Fig.10 Finite element model of single layer square tube

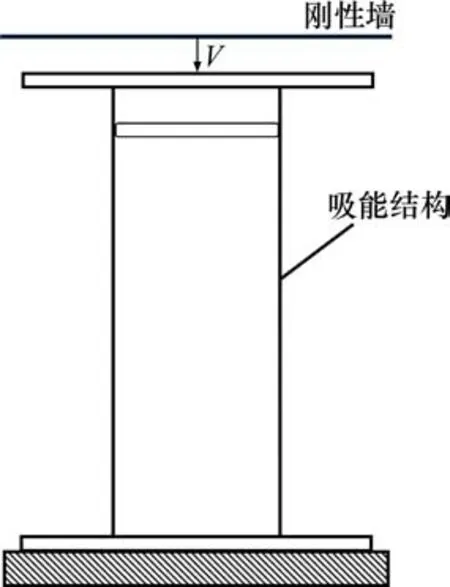
图11 刚性墙撞击示意图Fig.11 Velocity direction and position of rigid wall

图12是两者有限元模型压缩过程中的变形模式。从图中可以看到，2种吸能结构的变形模式均十分稳定有序，属于轴对称变形模式，并未出现混合模式以及延展性变形模式。图13是2种吸能结构轴向压缩后的力−位移曲线。可以发现，当增加了内管之后，初始撞击峰值力从635.58 kN增大到1 092.10 kN，增大了71.83%。吸能量从127.85 kJ增大到230.05 kJ，增大了79.94%，2种吸能结构的外管吸能量较为接近，因为增加的内管吸收了94.81 kJ的能量，从而显著提高了吸能结构整体的吸能量。

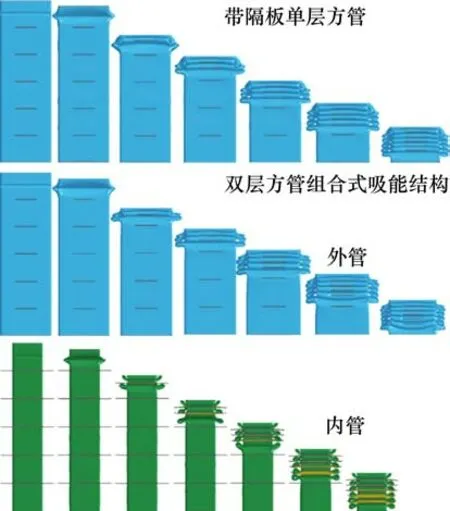
图12 吸能结构有限元模型变形模式Fig.12 Deformation process in simulation process

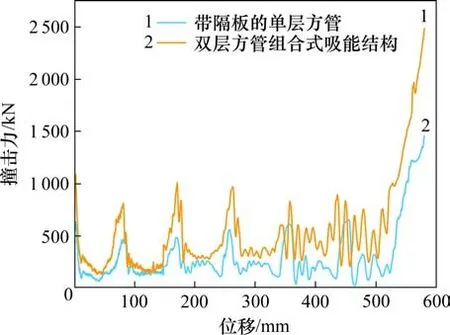
图13 2种吸能结构撞击力−位移曲线Fig.13 Force-displacement curves for two kinds of energy absorbers

4.2 诱导槽尺寸对吸能结构耐撞性影响

本节选取不同诱导槽尺寸的吸能结构为研究对象，A种外管诱导槽宽度为8 mm，深度为2 mm，内管诱导槽宽度为6 mm，深度为1.5 mm。B种外管诱导槽宽度为16 mm，深度为4 mm，内管诱导槽宽度为12 mm，深度为3 mm。C种外管诱导槽宽度为24 mm，深度为6 mm，内管诱导槽宽度为18 mm，深度为4.5 mm。D种无诱导槽。如图14所示，A，B和C 3种诱导槽长度方向贯穿方管两侧上端面。C和D 2种吸能结构在轴向压缩30 mm时变形模式如图15所示。可以清楚的看到，在缺少诱导槽的情况下，D种吸能结构在受到轴向动态冲击载荷时，并未从受冲击端开始变形，而是在多个位置同时发生变形，在整个压缩过程中，应力波从上到下传递，整个吸能管处于高应力状态，这样会严重影响吸能结构变形模式的有序性和稳定性。而在具备诱导槽的吸能结构中，由于诱导槽降低了管壁的强度，使得在诱导槽处首先发生变形。

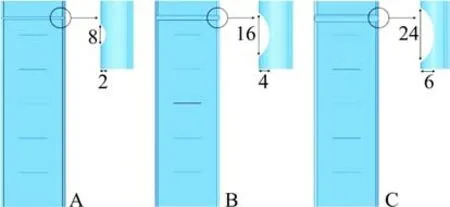
图14 不同诱导槽尺寸吸能结构示意图Fig.14 Schematic diagram of outer tube of energy absorber with different sizes of trigger

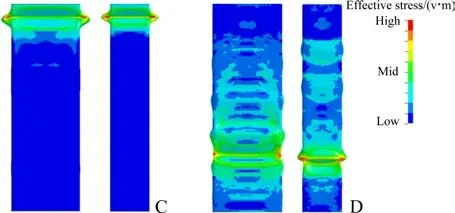
图15 吸能结构在轴向压缩30 mm时应力云图Fig.15 Stress nephogram

如图16所示，诱导槽的存在可以显著降低吸能结构在承受轴向冲击载荷时的初始撞击峰值力，随着诱导槽的宽度和深度增大，初始撞击峰值力逐渐减小。然而诱导槽的存在会使吸能结构吸能量减小。

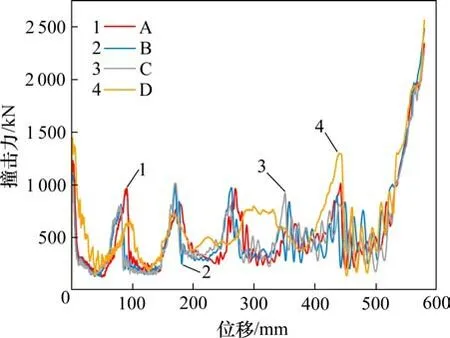
图16 不同诱导槽尺寸吸能结构撞击力-位移曲线Fig.16 Force-displacement curvesfor different sizes of trigger

4.3 隔板数量对吸能结构耐撞性影响

为研究隔板数量对轴向动态冲击下双层方管组合式吸能结构耐撞性的影响，本节选取无隔板，4隔板，5隔板和6隔板4种吸能结构进行研究。图17是吸能结构轴向压缩后变形模式截面图。从图中可以很清楚的看到，当无隔板时，内管与外管的变形模式比较混乱。在隔板数量为4和6时，内管与外管在变形过程中发生了明显的干涉，这样会影响吸能结构变形模式的稳定性。双层方管组合式吸能结构在隔板数为5时变形模式最为稳定有序。

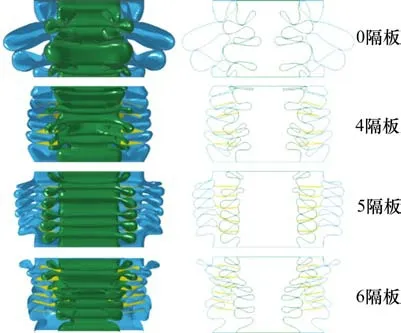
图17 吸能结构变形模式截面图Fig.17 Final deformation sections of tubes

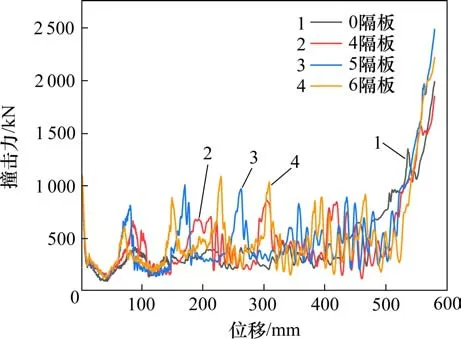
图18 吸能结构撞击力−位移曲线Fig.18 Force-displacement curves for different diaphragm number

通过观察不同隔板数目的吸能结构初始撞击峰值力可以发现，隔板数目与吸能结构初始撞击峰值力基本无关。对于双层方管组合式吸能结构，无隔板时对应的吸能量为187.82 kJ，相比之下隔板数4，5，6时对应的吸能量分别为222.35，230.05和234.18 kJ，增长率依次为18.38%，3.46%和1.80%，随着隔板数量的增多，形成的褶皱增多，吸能结构的吸能量逐渐提高，但趋势逐渐变弱。

5 结论

1)设计了双层方管组合式吸能结构，建立其有限元模型，在仿真计算中屈曲变形率先在诱导槽附近产生，并以远离撞击端方向依次发生渐进屈曲。一共产生6级屈曲变形，变形过程有序可控，并未发生失稳，屈曲变形较为完整。

2)基于吸能结构有限元仿真计算结果加工对应的试件实物并开展台车冲击试验。对双层方管组合式吸能结构在受到轴向动态冲击而变形的过程中的变形模式和力位移曲线与试验结果进行了对比分析。吸能结构台车冲击试验结果与有限元仿真结果基本吻合，有限元模型撞击结束变形模式与试验结果一致，试验与仿真结果误差在5%以内，考虑加工制造过程中残余应力以及不可避免的缺陷，该误差在可接受范围内，充分证明了有限元模型具有较高的精度，可以用来进行后续研究。

3)双层方管组合式吸能结构相比于带隔板的单层方管，变形模式同样十分稳定有序，初始撞击峰值力和吸能量显著增大。诱导槽的存在可以显著降低吸能结构在承受轴向冲击载荷时的初始撞击峰值力，随着诱导槽的宽度和深度增大，初始撞击峰值力逐渐减小。然而诱导槽的存在会使吸能结构吸能量减小。隔板数目与吸能结构初始撞击峰值力基本无关。双层方管组合式吸能结构在隔板数为5时变形模式最为稳定。随着隔板数量的增多，吸能结构的吸能量逐渐提高，但趋势逐渐变弱。