车流作用下大跨度拱桥车桥耦合振动分析

赵露薇，王青娥，王贵春

(1.中南大学 土木工程学院，湖南 长沙 410075；2.郑州大学 土木工程学院，河南 郑州 450001)

钢管混凝土拱桥因其造价合理、外形美观、施工方便和交叉性能强等独特优势，近几十年在我国得到了广泛应用[1−2]。移动车辆在桥面上行驶时，桥梁的显著动力响应和冲击效应是造成典型结构损伤的主要因素之一[3]。近年来，随着通行车辆行驶速度的不断提高和车辆超载情况的逐渐增多，一些新型大跨度桥梁在设计、建设、维修、养护过程中不断面临新挑战，因此有必要探究复杂工况下的车辆-桥梁耦合动力响应。学术界在该方面已取得一些成果[4]，车辆模型从最初的简单移动荷载[5]、移动的质量块、赋予质量的弹簧模型发展到具有多个自由度的质量−弹簧−阻尼体系[6]。构建桥梁模型时考虑的因素和参数也变得愈加复杂，包括伸缩缝构造[7]、桥梁跨度[8]和索塔构造[9]等。郝艳广等[10]基于ABAQUS有限元软件建立二自由度1/4车辆模型和简支桥模型，求解车辆和桥梁时域响应。BUCINSKAS等[11]将桥面和桥塔模拟为梁单元，采用单跨简化桥梁结构，基于结构−土相互作用研究车−桥−土系统的动力响应。LI等[12]对一座加固后的桥梁进行模拟，得到车辆行驶时的车速、车道位置、车辆重量和路面状况等对桥梁动力性能的影响。以上研究得到不同方面的有价值结论，但是多集中于单一移动车辆或单向车流在桥面上移动的工况，或仅仅分析桥梁结构的动力响应，极少涉及多个车辆双向交通流工况及车辆动力响应。这样不能模拟真实过桥车辆所引起在役拱桥的动力响应，而这却是桥梁维修管理部门关注的重点。同时，对于拱桥的研究，大多采用小跨度的单跨上承式或下承式桥梁，鲜少以大跨度中承式钢管混凝土系杆拱桥为研究对象[13−14]，然而针对两者的车桥耦合振动分析结果不尽相同。因此本文建立车桥系统三维动力分析模型，模拟双向多车辆的交通流分布，计算不同桥面不平度下茅草街大桥的动力响应，分析运行车辆在竖向、侧倾和俯仰3个方向的动力响应。车辆过桥时，主跨跨中部位、主拱部位的振动响应最为明显，也是研究桥梁安全性时的重点分析部位。因此，本文重点关注的结构响应包括桥梁跨中节点竖向振动位移、加速度峰值，桥梁跨中纵梁截面振动弯矩、正应力、剪应力幅值，主拱顶及主拱1/4处的轴力、正应力、剪应力幅值。为桥梁维修管理部门开展健康检测及制定维修决策提供理论依据。

1 车桥系统振动分析模型

1.1 茅草街大桥有限元模型

茅草街大桥的主桥为钢管混凝土系杆拱桥(三跨中承式)。桥梁上部结构包括桥面板结构、2根主拱肋、横撑、吊杆、立柱及若干连接件。桥面设计为双向4个车道，行车道宽15 m。桥梁有限元模型见图1。依据设计图纸建立桥梁有限元模型时的边界条件如下：横梁与纵梁固结，用自由度耦合模拟横梁和立柱的铰支状态；主墩桩基础的模拟采用边墩墩底及拱座均固结的形式。其中拱肋的模拟方法是将钢与混凝土经换算处理成同一种材料。换算公式如下：

式中：As,Ac为钢管的截面面积、钢管内混凝土的截面面积；Is,Ic为钢管截面惯性矩、钢管内混凝土惯性矩；Es,Ec为钢材弹性模量、混凝土弹性模量。

1.2 车辆空间模型

9自由度三轴车辆模型见图2，其中z1~z6分别为各车轮对应竖向位移；Zv，φv和θv分别为车体竖向位移、侧倾角位移和俯仰角位移；m1~m6分别为各车轮(包括车悬架)对应质量；mv为车体质量；ku1~ku6和cu1~cu6为各车轮对应车悬架刚度及阻尼；kd1~kd6和cd1~c d6为各车轮对应轮胎刚度和阻尼。

图2 车辆模型Fig.2 Vehicle model

1.3 桥面不平顺模拟

路面不平顺是引起车桥耦合振动的重要原因[15-17]。本文采用谐波叠加法模拟桥面不平顺，该方法的理论基础较为严密，计算结果稳定可靠。依照《车辆振动输入—路面平度表示方法》(GB7031)的等级划分，考虑到公路桥梁的实际路面情况，基于MATLAB模拟A，B，C和D 4个路面等级[18-20]，功率谱密度见式(2)。

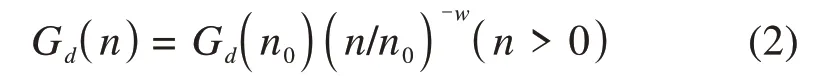
模拟桥面不平顺值的谐波叠加公式见式(3)：

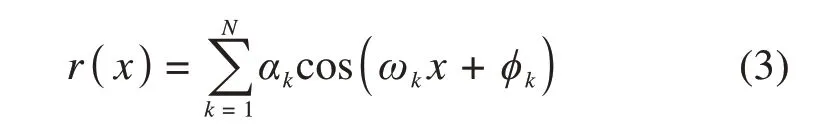
nk=nl+(k-1/2)Δn,k=1,2,…,N，为 空 间频率；Δn=(nh-nl)/N；nh和nl为空间频率的上、下限；圆频率ωk=2πnk；φk为相位角。

表1 参数的含义Table 1 Meaning of parameters

以B级桥面为例，分析结构动力响应，B级桥面情况下不平顺样本函数曲线及A，B，C和D 4个等级桥面的最大不平顺值，见图3。随着不平顺程度的提高，桥面不平顺值逐渐增大。A，B，C和D 4个不平顺等级对应的峰值依次是18.56，35.4，71.8和148.52 mm。与A级不平顺峰值相比，B，C和D 3个等级的不平顺峰值分别增大0.9倍、2.86倍和7.0倍。

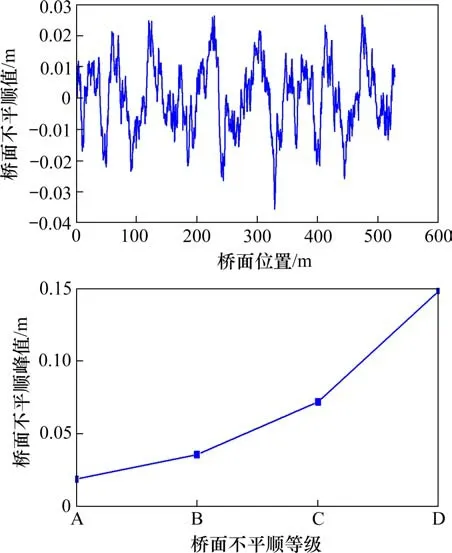
图3 B级桥面不平顺样本函数及各级桥面不平顺峰值曲线Fig.3 Grade B bridge deck irregularity sample function and the curve of maximum roughness values

1.4 车辆间距的模拟

区别于其他研究中单一移动车辆或单向车流移动的工况，本文模拟双向不间断车流，计算结果及结论更贴近实际。统计信息表明车辆间距具有随机特性且服从对数正态分布，考虑到车辆间距和车队数量，采用正态分布函数模拟随机车流。设x为车辆间距，y=lnx，则有

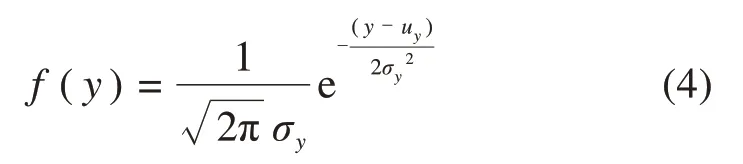
式中：f(y)是概率密度函数；uy是均值；σy是标准差。

2 车桥耦合振动微分方程及求解

2.1 方程的建立

在车桥耦合系统中，车辆和桥梁2个子系统通过位移协调条件和受力平衡条件形成一个整系统。位移协调条件指车辆在桥上行驶过程中，车轮始终与桥面保持紧贴，不发生脱离，即行驶中车辆的竖向位移受到桥梁竖向位移的限制与约束。同时，将桥面不平顺值与桥梁位移叠加组合而成的等效不平顺值作为激励，输入到车辆子系统中。受力平衡是指在车辆与桥面接触点上，车桥之间形成一对大小相等方向相反的作用力与反作用力平衡力系。运动方程写为式(5)和式(6)：

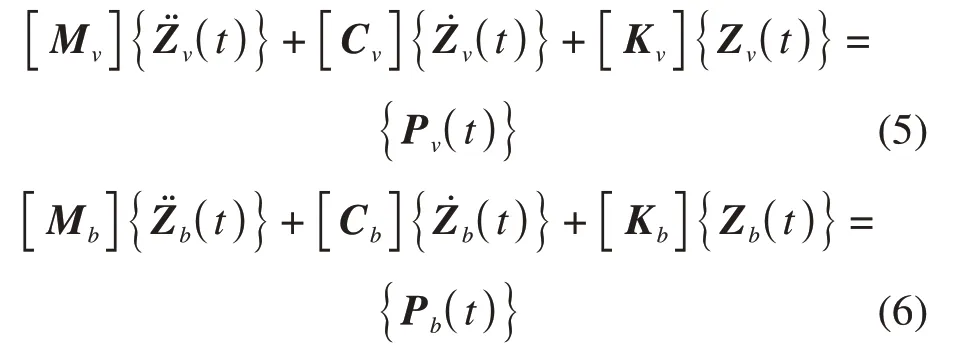
在式(5)和式(6)中，[M]为质量矩阵；[C]为阻尼矩阵；[K]为刚度矩阵；{Z(t)}为位移列向量；{̇(t)}为速度列向量；{̈(t)}为加速度列向量；{P(t)}为子系统所受作用力列向量；下角标v表示车辆子系统；下角标b表示桥梁子系统。

2.2 求解及收敛控制

采用Newmark-β法分离迭代求解车辆与桥梁的振动微分方程组，该算法具有较高的收敛性、效率及计算精度。利用ANSYS中的APDL语言，编写命令流进行迭代求解。位移收敛准则如下：

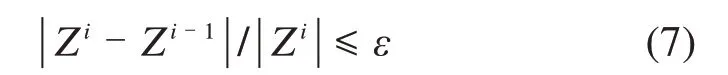
Zi，Zi-1分别表示第i次，第i-1次迭代车轮与桥面接触点处的竖向位移向量；ε为位移控制参数，取为0.01。

2.3 求解程序流程图

当车辆在桥面上行驶时，由于车辆所在位置一直在变化，桥面的不平顺值、车辆与桥梁的振动状态也随之变化，为时变随机的复杂过程。应用ANSYS模拟“车过桥”过程时，假定车辆和桥梁的初始位移、速度、加速度为0，桥面不平顺与桥梁位移叠加后的不平顺值为下一时间步的激励，作用于车辆与桥梁子系统。利用宏命令按照功能分块编制求解命令流，可极大降低修改工作量，缩短计算时间。APDL迭代求解命令流的流程见图4。

3 桥梁动力响应

仅考虑车辆荷载作用，双向不间断车流在桥面4车道匀速行驶，车速20 m/s，车重(自重+载重)20 t，每列车队的首个车辆同时上桥，桥面上车辆数目最多时为30辆，车辆质心在同一直线上，位于车道横向中部。

采用国家标准中A，B，C和D 4个不平顺等级，计算分析一个行车周期(桥梁跨度/行车速度)内桥梁的动力响应，结果见图5和图6。

1)桥梁跨中节点位移变化分析。如图5所示，桥梁跨中节点在不同路面等级下的竖向振动位移时程曲线和竖向振动加速度时程曲线，在“车过桥”过程中呈现出变化复杂的波动状态。中华人民共和国行业标准《钢管混凝土拱桥设计规范》中规定：对于拱桥结构，在汽车荷载作用下，一个桥跨范围内的正负挠度的绝对值之和不大于L/800。茅草街大桥总跨度为528 m，L/800=528×1 000/800=660 mm。在A级路面不平顺下，桥梁跨中节点竖向振动位移的峰值是1.335 mm，B，C和D等级对应峰值分别为2.871，8.129和10.874 mm。B，C和D 3个不平顺等级对应的峰值与A级对应峰值比较，分别增大1.15倍、5.09倍和7.15倍。可知，桥梁跨中节点竖向振动位移的峰值随路面不平顺程度的增加呈非线性增长，且都在容许变形范围内，桥梁处于安全状态。

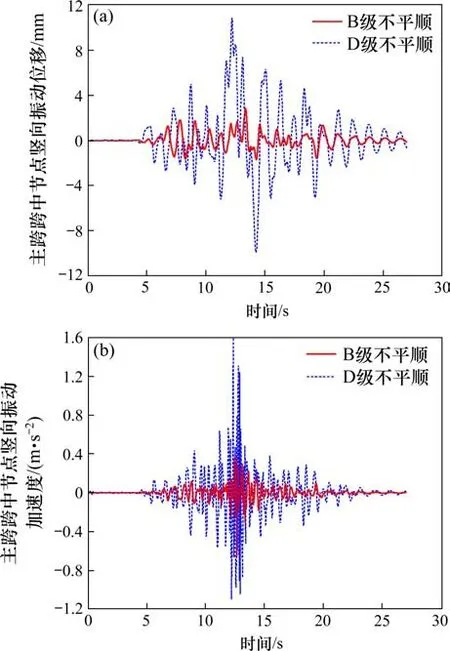
图5 桥梁跨中节点竖向振动位移、加速度时程曲线Fig.5 Time-history curves of vertical vibration displacement and acceleration

2)桥梁跨中节点加速度变化分析。路面等级为A时，桥梁跨中节点最大竖向振动加速度为0.385 m/s2，B，C和D等级对应峰值分别为0.657，0.928和1.596 m/s2。B，C和D 3个不平顺等级对应的峰值与A级对应峰值比较，分别增大0.71倍、1.41倍和3.15倍。从图6得出，桥梁跨中节点竖向振动加速度峰值随路面不平顺程度的增加呈非线性增长，加速度的增长幅度远小于位移增长幅度。

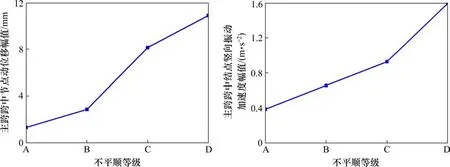
图6 不同路面等级桥梁跨中节点竖向振动位移、加速度峰值变化曲线Fig.6 Variation curves of vertical vibration displacement and acceleration peak value of mid-span joints of bridges with different pavement grades

3)桥梁跨中纵梁截面振动响应分析。各响应峰值如表2所示，路面等级为A时，桥梁跨中纵梁截面最大竖向振动弯矩为4.616 kN∙m，B，C和D 3个不平顺等级对应的峰值分别是6.934，11.327和24.605 kN∙m。B，C和D 3个不平顺等级对应的弯矩峰值与A级对应峰值比较，分别增大0.50倍、1.45倍和4.33倍。同样，B，C和D 3个不平顺等级对应正应力的峰值分别比A级对应正应力峰值增大0.41倍、1.67倍和3.16倍。B，C和D 3个不平顺等级对应剪应力的峰值分别比A级对应剪应力峰值增大1.32倍、4.30倍和6.95倍。因此，随着路面不平顺等级的增加，桥梁跨中纵梁截面的弯矩、正应力、剪应力均呈非线性增长，其中剪应力增长幅度较大，而正应力和弯矩的变化幅度较小，增长趋于平缓，且远小于钢梁的容许正应力200 MPa和容许剪应力120 MPa[21]，桥梁跨中纵梁处于安全状态，见图7。

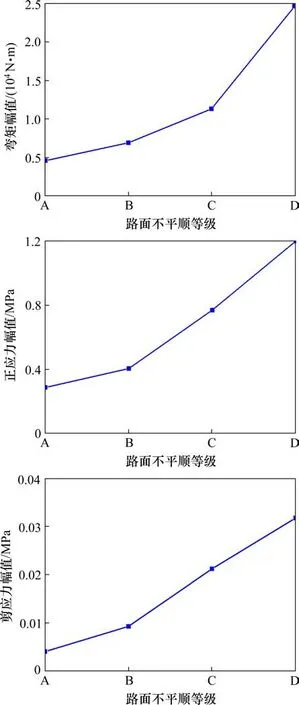
图7 桥梁跨中纵梁截面振动弯矩、正应力、剪应力幅值随桥面等级变化曲线Fig.7 Variation curve of vibration bending moment，normal stress and shear stress amplitudeof longitudinal beam section of the bridge with the grade of the bridge deck

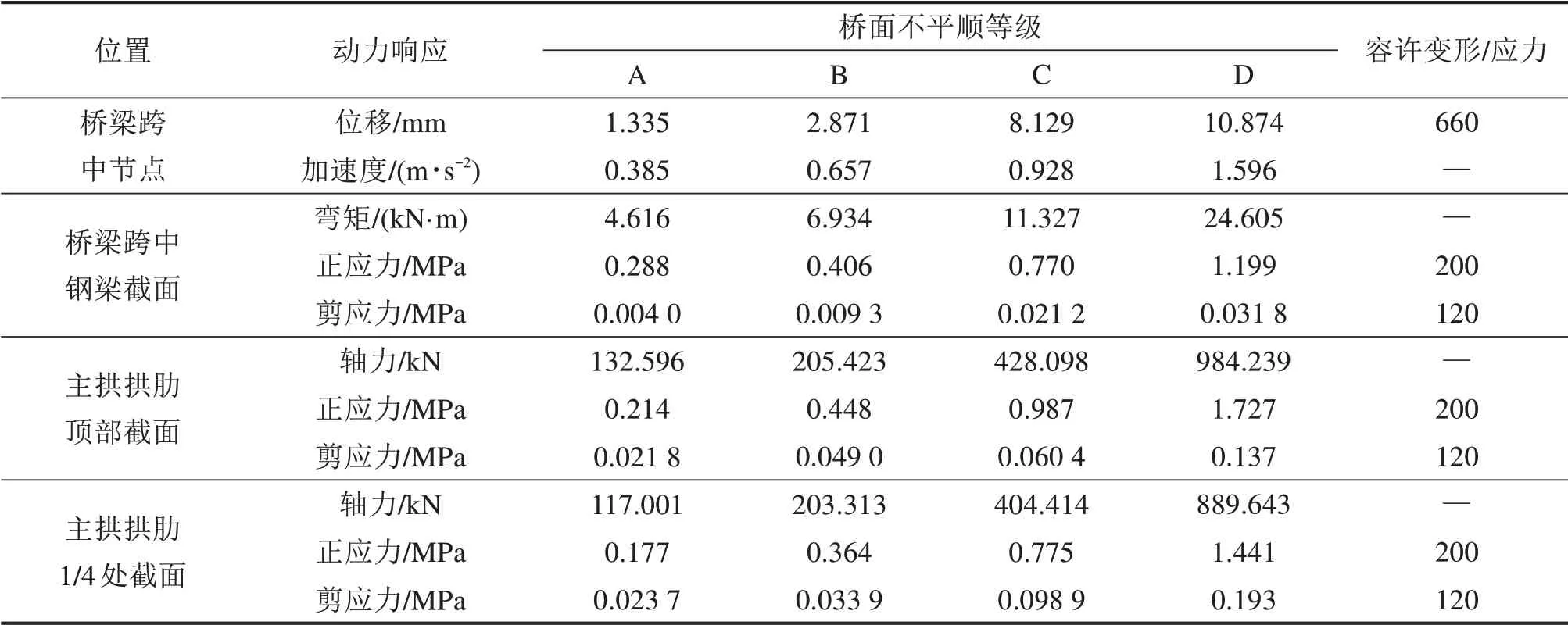
表2 不同桥面等级桥梁跨中、主拱动力响应峰值Table 2 Peak value of dynamic response of bridge mid-span and main arch under different bridge deck grades

以上分析说明路面等级越低，不平顺状况越恶化，车桥耦合振动越剧烈，桥梁跨中节点及截面的动力响应越明显。在桥梁日常维护中，应及时修补桥面，防止因桥面恶化引起结构较大的动力效应而导致桥梁发生损伤。

4)桥梁主拱拱肋顶部截面和主拱拱肋1/4处截面振动响应分析。随着路面等级的变化，拱顶截面和拱肋1/4处的轴力、正应力及剪应力呈非线性增长，见表2。总体上，拱顶截面应力响应峰值对桥面不平顺等级的敏感程度较拱肋1/4截面处的高。拱顶部截面和主拱拱肋1/4处截面的最大正应力值是1.727 MPa，最大剪应力值是0.193 MPa。而钢的容许正应力和容许剪应力分别是200 MPa和120 MPa，屈服应力是340 MPa。因此，该桥梁在正常使用阶段的受力性能能够满足要求。由表2可知，桥面不平顺对于主拱拱顶及主拱1/4处的正应力和剪应力影响均较小，主拱顶正应力变化范围是0.214～1.727 MPa，主拱顶剪应力变化范围是0.021 8～0.137 MPa。因此，可以得出桥面不平顺对主拱的受力影响较小。

4 车辆动力响应

1)车辆位移变化分析。图8～9分别是车辆竖向、侧倾和俯仰3个方向对应的位移和加速度峰值的变化曲线，各振动响应峰值列于表3。可以得到，B，C和D 3个等级下的车辆竖向位移分别是A级桥面不平顺对应位移的1.98倍、4.64倍和6.71倍；侧倾位移分别是A级的2.09倍、4.08倍和8.18倍；俯仰位移分别是A级的2.29倍、4.35倍和9.24倍，总体上俯仰位移的变化幅度大于竖向和侧倾2个方向的位移变化幅度。车辆各自由度对应的位移随桥面不平顺情况的恶化而逐渐增大，车辆在D级桥面行驶时的振动位移远远大于在A级桥面上的振动位移。因此，桥面不平整度会加大车辆的振动响应，影响司乘人员的舒适感。

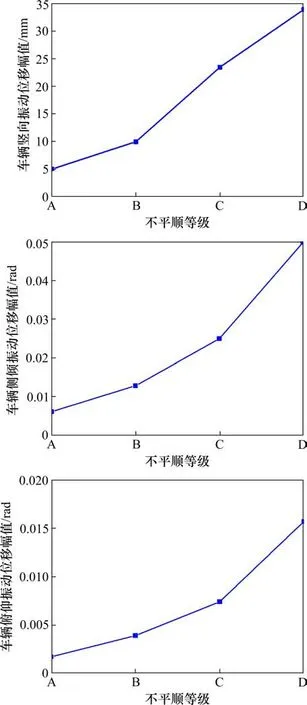
图8 不同路面等级下车辆竖向、侧倾、俯仰振动位移时程曲线Fig.8 Time-history curves of vertical，roll and pitching vibration of vehicles under different road grades

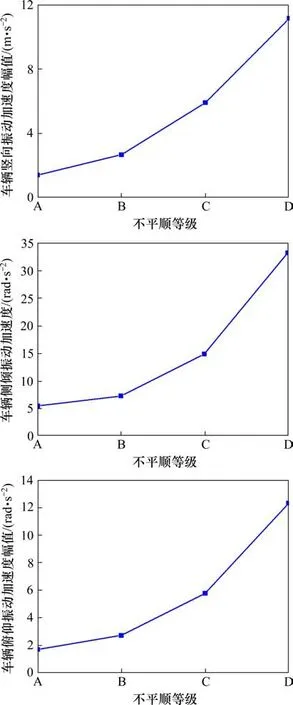
图9 车辆竖向、侧倾、俯仰振动加速度峰值变化曲线Fig.9 Peak acceleration curve of vehicle vertical，roll and pitch vibration

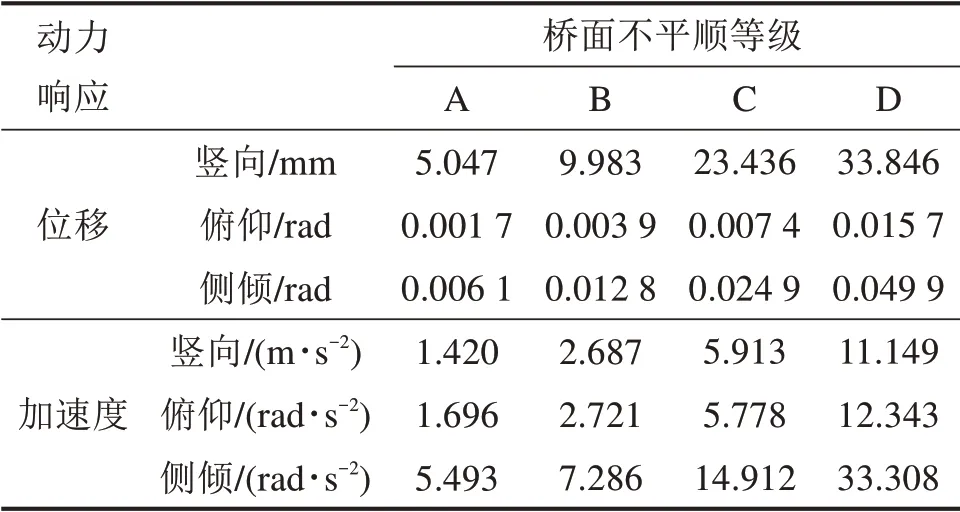
表3 不同桥面等级下车辆动力响应峰值Table 3 Peak dynamic response of vehicles under different bridge deck grades

2)车辆加速度变化分析。B，C和D 3个等级下的车辆竖向加速度分别是A级路面不平顺对应加速度的1.89倍、4.16倍和7.85倍；侧倾加速度分别是A级的1.32倍、2.71倍和7.27倍；俯仰加速度分别是A级的1.6倍、3.4倍和7.27倍。竖向加速度的增长幅度最大，俯仰、侧倾2个方向的加速度增长幅度稍小一些。随着桥面不平顺的恶化，车体各方向的振动加速度峰值均呈现非线性增长，将会极大影响车辆安全性。

5 结论

1)在“车过桥”过程中，桥梁跨中节点的竖向振动位移和竖向振动加速度时程曲线呈现出变化复杂的波动状态。随着路面的恶化，桥梁跨中节点竖向振动位移峰值、加速度峰值呈非线性增长，D级较A级的位移峰值增大7.15倍。但都在容许变形范围内，桥梁处于安全状态。

2)随着路面不平顺程度的增大，桥梁跨中截面振动弯矩、正应力和剪应力幅值在逐渐增加，呈非线性增长。这说明桥面不平顺度的增大会加剧车桥耦合振动，从而加大跨中截面、主拱的动力响应。D级与A级相比，跨中截面弯矩峰值增大4.33倍，正应力峰值增大3.16倍，剪应力峰值增大6.95倍；主拱正应力峰值增大7.07倍，剪应力峰值增大5.28倍，在正常使用阶段的受力性能能够满足要求。但在开展大跨度拱桥结构设计中，仍需将不平顺影响考虑在内。

3)车辆的竖向、侧倾、俯仰3个自由度对应的位移、加速度均逐渐增大，且增大趋势愈加明显，因此要注意桥面平整度的维护。

4)本研究集中于路面不平度变化时钢管混凝土拱桥与行驶车辆的车桥耦合振动响应，今后可采用试验和数值模拟方法探讨车速变化时钢管混凝土拱桥在移动车辆荷载作用下的动力性能，还可考虑分析车辆安全性及司乘人员的乘坐舒适性。