基于Maxwell分布的砂岩本构模型研究

童立红，吴琳琳，徐长节

(1.华东交通大学 省部共建轨道交通基础设施性能监测与保障国家重点实验室，江西 南昌 330013；2.华东交通大学 江西省岩土工程基础设施安全与控制重点实验室，江西 南昌 330013)

人类进行生产和活动的地球表面层主要由岩石圈构成，其中80%为沉积岩[1]，受地理环境和自然风貌的影响，各地岩石的矿物成分、颗粒结构和物理力学性质等皆不相同，甚至同一岩石的各部分性质也因其内部不规则分布的微裂纹和微孔隙的不同而略有差异。通过研究岩石本构关系来了解岩石在受力过程中的变形和破坏特性一直是学者们的研究热点之一。早在1982年，KRAJCI‐NOVIC等[2]基于统计强度理论思想对损伤进行了定义，并将之融入到岩石本构关系中，以此研究岩石力学破坏机制。国内外学者在此基础上展开了一系列研究，带来许多创新成果。大量试验表明，在传统本构关系中引入数理统计方法来描述岩石应力-应变关系或损伤演化关系是合理的。CAO等[3]使用正态分布来描述微元强度分布，进一步建立了损伤本构模型，该模型仅包含常见的明确的物理参数，应用简单，但其可能出现参数为负的情况，不符合客观事实。蒋维等[4]选择对数正态分布来构建本构模型，很好地解决了使用正态分布过程中出现的参数为负的现象。然而，更多学者[5-10]认为岩石微元强度破坏服从Weibull分布，以此构建的损伤本构模型能够很好地描述岩石变形的全过程，尤其是低应变水平下的初始阶段和屈服后的残余变形阶段。在此基础上，通过运用不同的强度准则来描述岩石在不同环境下的破坏特征。例如：基于Mohr-Coulomb准则构建的岩石损伤演化模型，刘树新等[11-12]引入第3个参数对模型进一步修正，更好地解释了岩石峰后变形特征，王苏生等[13]引入孔隙水压力，研究了孔隙率对损伤阈值的影响；王辉等[14-15]利用Drucker-Prager强度准则建立岩石损伤演化模型，结果表明Weibull分布参数F0，m在不同受力情况下都具有合适的物理基础，进一步证明了模型的适用性；高玮等[16]假定应力水平满足Hoek-Brown准则，从而建立泥质砂岩破裂本构模型，并用数值模拟试验再次验证了模型的可靠性；刘之喜[17]认为裂纹数服从Weibull分布且裂纹扩展服从Griffith准则，建立了高围压下岩石循环加-卸载统计损伤本构模型。此外，周峙等[18]假设裂土微元强度服从Laplace分布，并考虑初始损伤的影响，建立了干湿循环作用下的损伤演化模型。然而，上述统计分布模型的使用均是基于经验而提出，缺乏相关的严格推导和理论基础。尤其是使用最广泛的Weibull分布，其分布参数F0，m的求解方法不一[7]，早期人们使用线性回归法和反演分析法，前者计算简便但参数本身无明确物理意义，后者相对精确但对试验数据要求较高，后期研究发现峰值点法不仅处理简便且物理意义较清晰。然而，使用峰值点法得到的分布参数的物理意义是对试验结果的唯象描述，缺乏本质的物理基础。TONG等[19]基于统计力学基本理论，认为破坏微元强度需要的能量以最概然分布的形式存在，经过严密的论证证明颗粒材料的微观接触状态符合Maxwell分布。尽管TONG等[19]的推导是针对无黏性颗粒材料提出，但是经过数学分析发现，其可以直接适用于黏性或者胶结颗粒组成的材料系统。因此，本文在其研究基础上，假设砂岩微观颗粒状态服从Maxwell分布，基于Lemaitre应变等价原理构建砂岩本构模型，并通过室内试验对其进行验证。

1 构建本构模型

砂岩主要由砂粒胶结形成，具备明显的颗粒结构特征。云南砂岩属于泥质砂岩，颗粒细腻，其由不同尺寸的微观颗粒相互胶结而成，一般认为，不同颗粒之间的胶结强度不同，随着应变的增加，低强度的胶结键先破坏，高强度的胶结键后破坏[20]。承受荷载时，当微观颗粒胶结键破坏达到一定数量时，表现出宏观上的整体破坏。从统计力学的角度来看，不同强度胶结键的破坏规律符合某种统计分布，由于微观颗粒的数量足够多，可以认为胶结键破坏强度是连续分布的。这里假设每个胶结键都对应一个能量状态，由于岩石经过足够长时间的沉积后，其达到了最稳定的状态，则该状态对应的是胶结键能量的最概然分布。当外部荷载足够大时，或者输入的破坏能量足够高时，部分胶结键的能量不足以抵抗外部破坏能量，则这部分胶结键会产生破坏，宏观上表现为岩石强度的下降。假设每个胶结键的破坏能量以变形势能的形式存储在颗粒系统中，根据TONG等[19]的工作，颗粒接触能量对应的应变符合Maxwell分布，即岩石系统颗粒产生破坏的概率密度函数为：

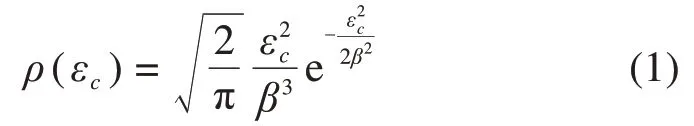
式中：εc为颗粒接触能量对应的应变；β2为岩石系统能量密度的参数。

当外部施加荷载后(即输入了破坏能量，这里以三轴压缩为例)，岩石产生轴向应变ε。根据上面的阐述，对于接触应变εc∈[0,ε]的胶结颗粒将会产生破坏，因此岩石系统颗粒产生破坏的概率为：

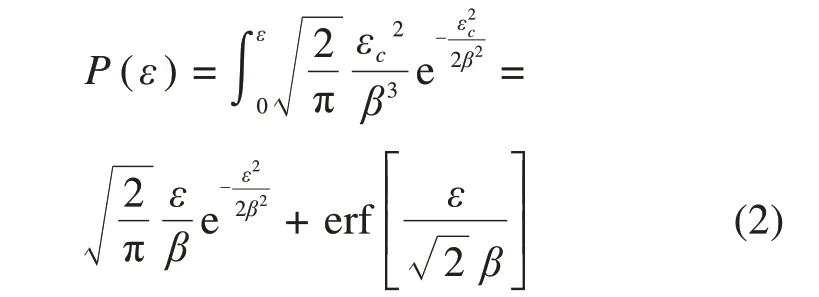
式中：erf(ε)为误差函数。

根据Lemaitre应变等价理论[21]，名义应力作用在受损材料上引起的应变与真实应力作用在相同的无损材料上引起的应变是相同的，即：

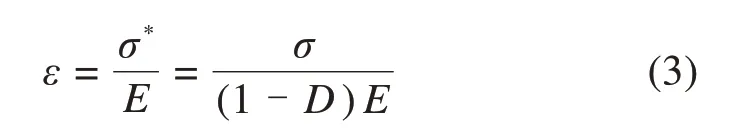
式中：σ*为真实应力；E为弹性模量；σ为名义应力；D为损伤变量。

若受损岩石单元即受损岩体不再为整体提供强度，则：

假设在受力过程中未损伤岩体仍然满足广义虎克定律，可得：

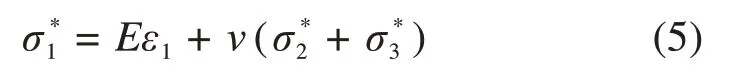
式中：ν为泊松比。

把式(4)代入式(5)，且两边同时乘以1-D可得：

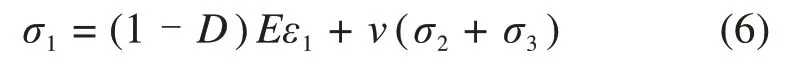
在本试验中，先施加围压至预定值，再施加轴压直到岩样破坏。其中σ2=σ3，因此，可以对式(6)进一步简化得到式(7)。

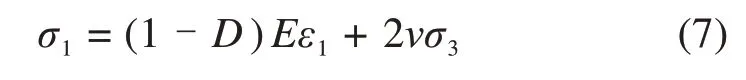
由于所施加轴向应力为偏应力，即试验数据中的轴向应力σ如式(8)所示。因此，在试验应力-应变曲线记录之前会产生一个初始应变ε0，其大小如式(9)所示。

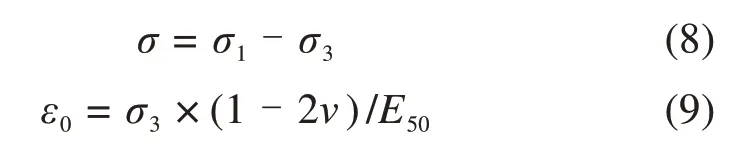
式中：σ3为围压；E50为50%峰值强度处的割线模量。

综合式(7)~(9)，可以得到应力-应变关系如下：

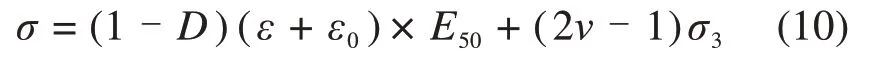
由式(2)可知微元破坏的概率为P(ε)，其认为微观颗粒间胶结键的方向均为垂直或水平结构，而实际上胶结键方向是随机分布的。通过对试验数据进行分析可知，对P(ε)进行α次幂处理，可以很好地解决该问题，使其更符合客观事实。因此，破坏微元数量占总微元数量的比例为Pα(ε)，则，可定义损伤变量D如式(11)所示。

把式(11)代入式(10)中，可得岩石本构模型如下：

2 试验与模型验证

2.1 试验

为验证本文所提出的本构模型的适用性，本文采用型号为ZTRE-210的微机控制岩石三轴测试系统展开了一系列不同围压下的三轴压缩试验。试验所用微机控制岩石三轴压缩系统如图1所示，使用轴向和环向应变计实时测量记录轴向应变和环向应变。该试验设备最大试验荷载为2 000 kN，最大围压为100 MPa。按照国际岩石力学学会试验委员会的规定，将来自云南省楚雄彝族自治州武定县的红砂岩沿沉积方向取芯制成∅50 mm×100 mm的标准圆柱体试样，试样表面光滑、色泽均匀、上下切面平整，如图2所示。

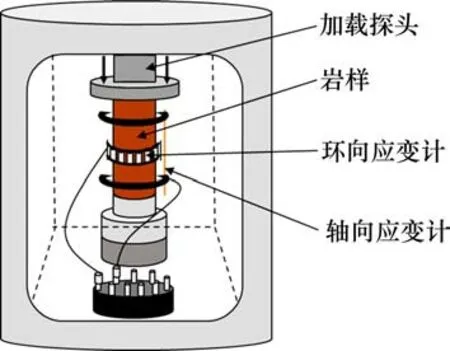
图1 微机控制岩石三轴压缩系统示意图Fig.1 Schematic diagram of microcomputer controlled rock triaxial compression system

图2 砂岩试样Fig.2 Sandstone sample

试验时，首先施加1 kN的压力使加载探头与试样顶面接触预压，保证试样处于轴心受压状态；接着施加围压至设定值(分别为0，4，7和10 MPa)，稳定后施加轴压直至试样破坏，其中加载速率为0.02 mm/min；最后，先卸载轴压再卸载围压。试样破坏形式如图3所示，均为剪切破坏。如图3(a)和3(b)所示，在围压为0和4 MPa时，岩样破坏比较严重，存在多条裂缝且缝隙较大；在围压为7 MPa和10 MPa时，如图3(c)和3(d)所示，岩样主要存在一条主裂缝且缝隙较小，说明较大围压约束了岩石剪切面的发展。

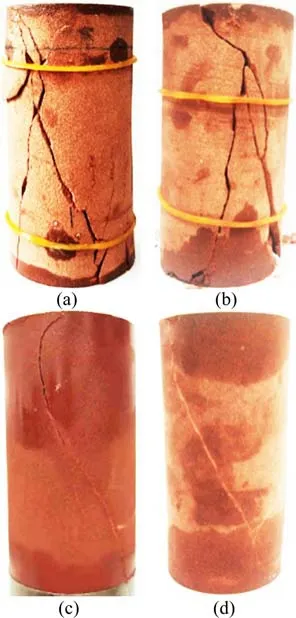
图3 试样破坏图Fig.3 Specimen failure diagram

2.2 模型验证

在本构模型式(12)中，围压σ3为已知量，割线模量E50和泊松比ν通过应力-应变曲线获得，初始应变ε0通过式(9)计算得到，未知量Pα(ε)取决于参数α和β。因此，通过对试验曲线进行非线性拟合可得到参数α和β，不同围压下的曲线拟合结果如图4所示。由图4可知，在不同围压条件下试验数据与理论曲线都吻合良好，且理论曲线能较好地反映应力-应变关系的各个阶段。

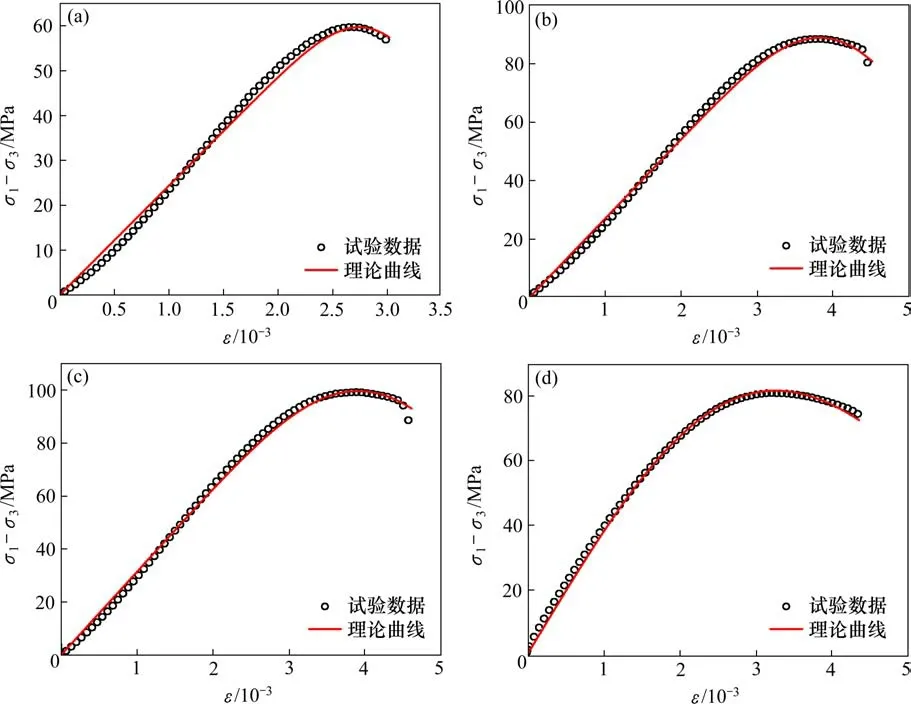
图4 应力-应变曲线及其理论曲线Fig.4 Stress-strain curve and its theoretical curve

3 讨论与分析

3.1 模型参数的物理意义

为了明确参数α和β的物理意义，将其中一个参数固定，改变另一个参数，由式(12)得到2组应力-应变曲线，如图5所示。由图5(a)可知，保持α不变，每当β上升20%，峰值强度也随之上升20%，且峰值右移，但其峰值附近的弯曲程度基本一致，即β的大小反映了岩石的宏观强度和韧性，β越大岩石的强度越高、延展性越好。由图5(b)可知，保持β不变，每当α上升20%，峰值强度随之上升10%，峰值也发生右移，说明α的大小对岩石强度和延展性也存在影响，但其影响峰值强度的能力弱于参数β。因此，可以将参数α和β视为岩石强度和延展性的指标。

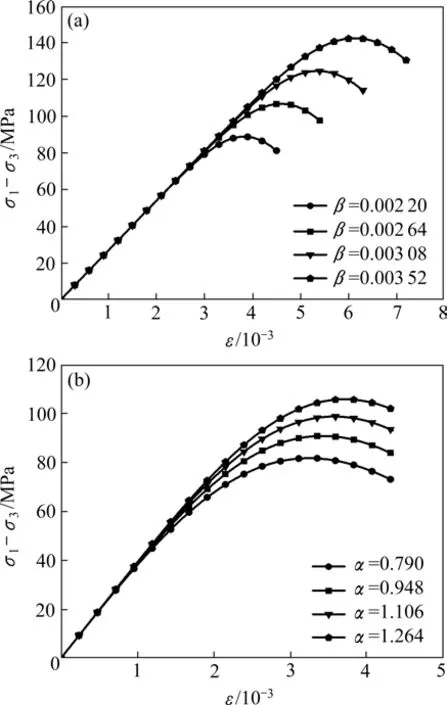
图5 参数变化示意图Fig.5 Schematic diagram of parameter change

3.2 围压对模型参数的影响

根据式(12)拟合得到的模型参数如表1所示，参数α随着围压的增大而减小，参数β随着围压的增大而增大。为了更直观地描述围压与模型参数之间的关系，对表1中的数据进行数学拟合，拟合结果如图6所示。由图4可知，随着围压的增大，岩样峰值强度增大，屈服过程逐渐平缓，围压增强了岩石抵抗压缩变形的能力。结合上一节内容，如图6(a)所示，参数α与围压存在良好的线性递减关系；如图6(b)所示，参数β与围压呈二次递增关系。

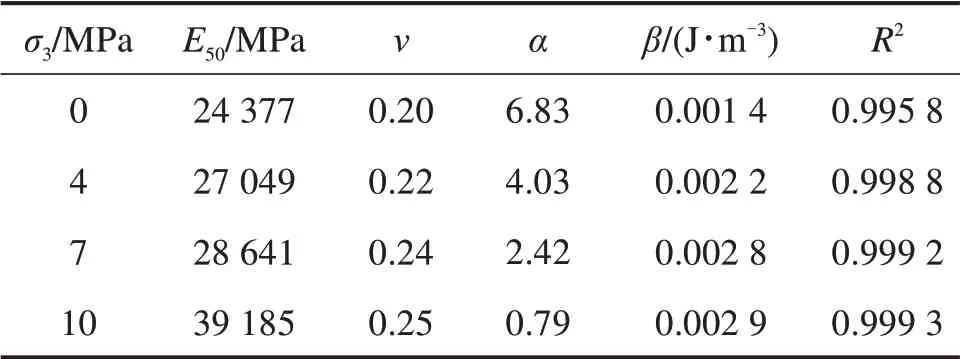
表1 参数拟合结果Table 1 Parameter fitting results

3.3 不同围压下的损伤演化规律

利用式(2)可得到微元破坏概率与应变的关系，如图7所示。在不同围压下，当应变较小时，微元破坏概率趋于0，且随着围压的增大其趋于0的应变区间变大。这是因为较大的围压提升了接触颗粒的变形能，即颗粒储备更高的抵抗破坏的能量，因此，在相同的能量输入条件下，其内部颗粒接触产生破坏的总量减少，对应图7中概率P的减小，即围压遏制了试样的破坏发展。

由式(11)可得损伤与应变的关系，进而得到不同围压下的D～ε关系曲线，如图8所示。损伤在经过初始为0的阶段后随着应变的增大而增大，破坏时的损伤值也随着围压的增大而增大。但当围压为10 MPa时，损伤曲线并未按照0～7 MPa下损伤的发展规律演化，主要是因为在施加高围压的同时，会产生部分初始的颗粒破坏损伤，在图8中表现为损伤曲线的左移，即对应10 MPa围压的情况。但是，从图8还可以发现，曲线发展后期的斜率随着围压的增大而减小，说明围压的增大依然可以有效地抑制损伤的发展程度。

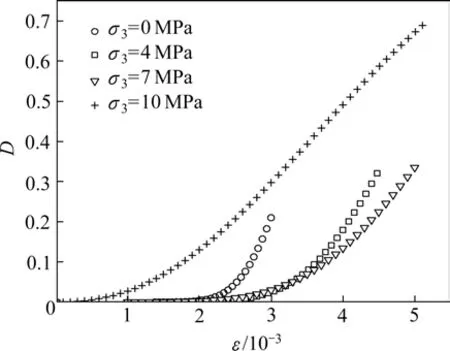
图8 损伤与应变的关系Fig.8 Relationship between damage and strain

4 结论

1)运用数理分布模型来构建岩石本构关系是一种常见的方法，在以往研究中，分布模型的选用通常基于经验主义，且其分布参数缺乏明确的物理意义。为了解决上述问题，本文基于统计力学基本理论，认为微元强度破坏所需能量以最概然分布的形式存在，采用经过严格推导论证的Maxwell分布构建了砂岩本构理论。通过室内试验对比分析，验证了模型的适用性，结果表明，该本构模型能很好地反映应力-应变曲线的各个阶段。

2)模型参数α和β具有明确的物理意义。从微观角度上看，α反映微观颗粒胶结键的方向，β表示试样压缩性能的强弱；从宏观角度上看，α和β反映岩石的宏观强度和延展性，且β对峰值强度的影响较α更强。

3)参数α与围压存在良好的线性递减关系，而参数β与围压呈二次递增关系。