基于随机森林的铁路冷藏运输需求预测
2022-05-17夏伟怀刘嘉莉冯芬玲
夏伟怀,刘嘉莉,冯芬玲
(中南大学 交通运输工程学院,湖南 长沙 410075)
铁路冷藏运输需求预测对推进铁路冷藏运输的发展具有关键作用,合理的铁路冷藏运输需求预测能够明确铁路冷藏运输需求的发展趋势,为铁路冷藏运输相关部门组织冷藏运输提供支撑。常用的预测模型可分为以时间序列分析法为理论基础的预测模型和以机器学习为理论基础的预测模型2种[1]。LIU等[2]利用二次指数平滑法预测了京津冀地区生鲜农产品的冷链物流需求量。王秀梅[3]提出了基于偏最小二乘法、ARIMA法和二次指数平滑法的权重分配组合法预测农产品冷链物流需求趋势。以时间序列分析法为理论基础的预测模型简单易行,短期预测精度较好,但预测模型仅关注内生变量而不关注外生变量,对数据的转折点缺乏鉴别能力,难以预测非稳定数据。近年来,以机器学习为理论基础的预测模型在各领域广泛应用。KHASANAH等[4]提出了基于SOM-SVR的两阶段预测模型预测生鲜食品的需求量,通过比较非聚类数据预测结果和基于SOM-SVR两阶段预测模型预测效果,得出聚类数据能够提高预测模型的准确性和实用性。HASSAN等[5]将时间序列模型与机器学习算法结合,构建了滚动学习框架以预测货运量。陈琛等[6]基于频繁港口和神经网络构建了考虑时空因素的货运量预测模型。DELLINO等[7]提出通过2种替代方法动态选择最合适的生鲜食品预测模型。李万等[8]通过改进粒子群算法优化长短时记忆神经网络预测铁路客运量。学者们从不同的角度阐明了以机器学习为理论基础的预测模型的优点。但铁路冷藏运输系统是一个非线性的复杂系统,系统内影响因素众多且相互渗透,且铁路冷藏运输系统可用的历史数据较少,增加了预测难度。目前研究冷藏运输需求预测的文献较少,常用模型中多元线性回归预测模型通过构建冷链运输需求量与其他相关因素的数学回归关系来预测冷链运输需求量,但其输入变量难以选择,且在处理非线性问题上预测效果较差;神经网络预测模型本身存在网络结构难以确定、学习速度慢和易陷入局部最优等问题[9];SVM在解决小样本、非线性和高维模式识别问题等方面具有突出优势,但SVM的参数一直没有很好的确定方法[10]。而随机森林作为集成学习的代表之一,大量的理论和实证研究都证明了随机森林具有很高的准确率,对异常值和噪声具有很好的容忍度,且不易出现过拟合[11−13]。基于此,本文利用Spearman相关分析结果进行特征筛选后,构建基于随机森林的铁路冷藏运输需求预测模型,以预测未来3个月的铁路冷链货运量。
1 模型构建
随机森林(random forest,RF)[14]是2001年由LEO BREIMAN将Bagging集成学习理论与随机子空间方法相结合,提出的一种机器学习算法,它是Bagging的一个扩展变体。随机森林在以决策树为基学习器构建Bagging集成基础上,进一步在决策树的训练过程中引入了随机属性特征。随机森林一般用于解决分类或回归问题。本文的研究重点是利用随机森林解决回归问题,而随机森林回归的基本思想是:首先利用自主抽样法从原始训练集抽取k个样本,且每个样本的样本容量均与原始训练集相同;其次对k个样本分别建立k个决策树模型,得到k种回归结果;最后通过取平均值组合k个决策树结果[15]。基于随机森林回归的基本思想,构建基于随机森林的铁路冷藏运输需求预测模型的主要步骤为:
1)影响因素分析。依据国内外现有研究情况,同时考虑到数据的可获性,分析影响铁路冷藏运输需求的因素。
2)特征变量的选择。基于影响因素分析情况,利用Spearman相关性分析确定模型输入变量。
3)模型参数确定。决策树模型的数量和节点最大特征数是随机森林回归预测模型最主要的2个参数,本文利用网格搜索循环遍历所有候选参数,并以交叉验证结果作为指标得到优选参数。
4)模型训练。对随机森林回归模型进行训练,将优选参数组合应用至随机森林回归预测模型。
5)模型求解。将测试机数据输入至决策树,得到每棵决策树的回归结果,取平均值即为模型预测结果。
6)模型评价。本文选取平均绝对误差(Mean Absolute Error,MAE),平均绝对百分比误差(Mean Absolute Percentage Error,MAPE),均方根误差(Root Mean Square Error,RMSE)和拟合优度R24个模型评价指标对模型预测效果进行评价。
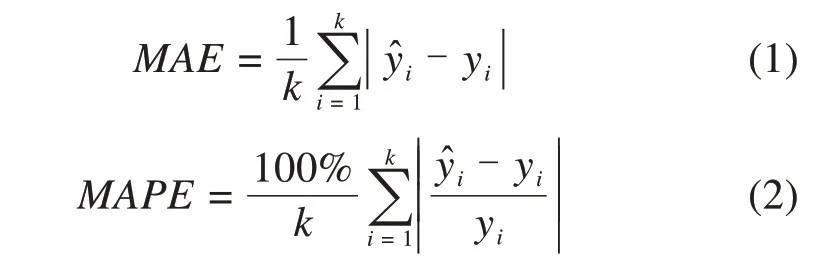
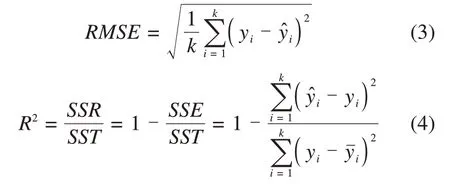
式中:和yi分别为预测值和实际值;k为预测样本数;为yi的平均值。
依据以上步骤,得到基于随机森林的铁路冷藏运输需求预测模型的流程如图1所示。

图1 随机森林回归预测模型流程图Fig.1 Flow chart of random forest regression prediction model
2 实证分析
2.1 数据来源
基于已有文献研究及对实践中影响铁路冷藏运输需求变化的因素分析来整合查找影响因素,结合数据可获取性原则,统计相关数据。本文涉及到的数据取自国家局、中国指数网以及中铁特货物流股份有限公司。
2.2 影响因素分析
2.2.1 消费经济水平
消费经济水平方面主要从宏观层面分析影响铁路冷藏运输需求的因素,其主要包含消费水平和经济发展水平2个方面。其中消费水平是指一定时期内消费者用于满足自身日常生活费用各项支出的总和。消费水平能够体现人们的购买力情况。学者主要选用农村居民消费水平、城镇居民消费水平、价格指数等作为消费水平影响因素以预测冷链的需求量[16−17]。居民消费水平和价格指数从不同角度反映消费水平的变化,其中居民消费水平指标一般按年统计,可作为中长期预测指标,价格指数指标可按月、季、年统计,既可作为短期预测指标,也可作为中长期预测指标。本文旨在预测铁路冷藏运输的月需求量,选取食品类居民消费价格指数、食品类商品零售销售价格指数作为衡量消费水平的主要指标。
经济发展水平是指一个国家经济发展的规模、速度和所达到的水准。现有研究中学者大都选取GDP、第一产业增加值、第三产业增加值、产业结构比例、社会消费品零售总额等指标衡量经济发展水平[16-18]。本文旨在分析铁路冷藏运输的短期预测,而GDP和产业结构等指标大都是按年统计,适用于中长期预测,因此本文主要选取社会消费品零售总额作为衡量经济发展水平的预测指标。
2.2.2 行业水平
铁路冷藏运输即通过铁路实现冷藏运输,因此它不仅受到物流行业发展的影响,也受到铁路行业发展的影响。现有研究中,学者主要从交通条件、载货条件、固定资产投资等方面反映行业发展水平,其中交通条件通过路网条件体现,常用指标有铁路营业里程;载货条件通过设施设备拥有量以及载货量体现,常用指标有铁路机车产量、冷藏车保有量、冷库容量、铁路货运量等;固定资产投资体现固定资产的再生产情况,体现一定时期内在行业内的投入规模,常用固定资产投资额指标[16−18]。本文旨在分析铁路冷藏运输需求量的短期发展趋势,铁路路网条件在短期内较为稳定,因此主要从载货条件和固定资产投资情况分析行业水平,基于铁路行业和冷链行业的特性,考虑数据可获取性,选取铁路机车产量、金属集装箱、铁路货运量、物流景气指数和铁路运输业固定资产投资额作为衡量行业水平的主要指标。
2.2.3 供需水平
由经济学中供求理论可知,商品的供给和需求其实是由商品生产自身所决定。因此本文的供需水平主要从铁路冷藏运输对象的供需情况入手,由《中国冷链物流发展报告》(2019)可知,铁路冷链运输对象主要为水果、蔬菜、肉类、水产品、乳制品和冷冻产品六大类货物,因此主要从六大类货物的供需情况入手,梳理供需水平影响因素。选取鲜、冷藏肉产量、乳制品产量、饮料产量作为衡量供给量的主要指标,选取粮油、食品、饮料及烟酒类商品零售值作为衡量冷藏运输的需求量指标,为了更加全面反映供需水平选取农副产品类购进价格指数、食品工业生产者出产价格指数作为间接反映供需水平的指标。
依据以上分析,本文选取的影响铁路冷藏运输需求因素如表1所示。

表1 影响因素Table 1 Influence factors
2.2.4 特征选择
利用SPSS软件中的相关功能,对14个特征变量以及预测目标值铁路冷链货运量(y)进行Spear‐man相关性分析,选取与预测目标值铁路冷链货运量相关性显著的特征变量作为铁路冷藏运输需求预测模型的输入变量,Spearman相关性分析结果如图2所示。
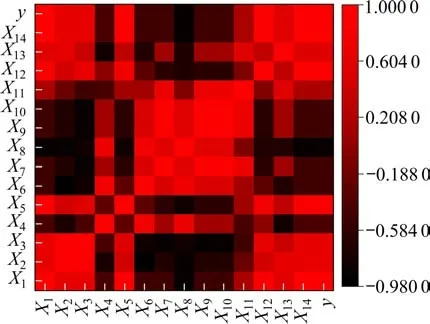
图2 Spearman相关系数矩阵Fig.2 Correlation matrix of the variables
由Spearman相关性分析结果可知X1和X14在0.01级别与预测目标值铁路冷链货运量相关性显著,X6,X8和X9在0.05级别与预测目标值铁路冷链货运量相关性显著。基于以上分析,选取X1,X6,X8,X9和X14作为输入变量,并重新标号,具体如表2所示。

表2 特征变量的编号及名称Table 2 Number and name of characteristic variable
2.3 结果分析
2.3.1 模型参数确定
利用Bootstrap抽样方法将数据集分为训练集和测试集。将数据样本中的2/3作为训练集样本,以训练建立模型,剩余的1/3作为测试集样本,以用于测量模型的预测性能。利用网格搜索方法对参数寻优,计算得到优选参数如表3所示。

表3 预测模型参数选择Table 3 Parameter selection of prediction model
基于网格搜索方法,研究在不同参数组合下预测模型的MAE和R2变化趋势,MAE变化趋势如图3所示,R2变化趋势如图4所示。
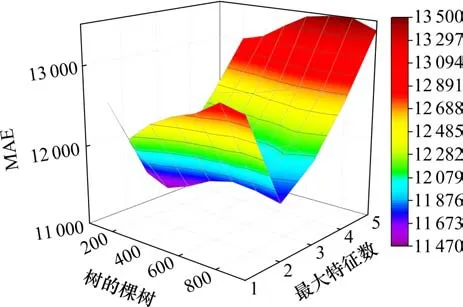
图3 不同参数组合下MAE变化趋势Fig.3 Trend of MAEvariation under different parameter combinations
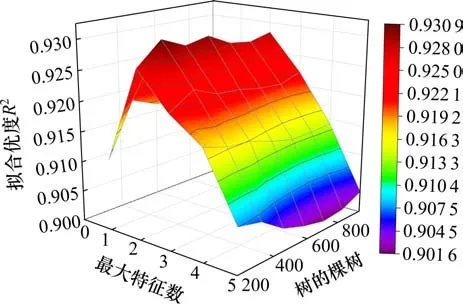
图4 不同参数组合下R2变化趋势Fig.4 Trend of R2 variation under different parameter combinations
由图3和图4可知,相较于决策树数量,最大特征数的变动会导致MAE发生较大波动,且呈现先下降后上升的趋势,在最大特征值为2时是拐点,而不同参数组合下拟合优度R2的值相差不大。
2.3.2 模型对比
将RF预测值与实际值进行对比,如图5所示。
由图5可知,总体而言,经过Spearman相关分析后进行特征筛选的随机森林回归预测模型预测值线图与实际值的线图变化趋势大体相似,表明模型能够较好地预测铁路冷藏运输需求发展趋势变化。
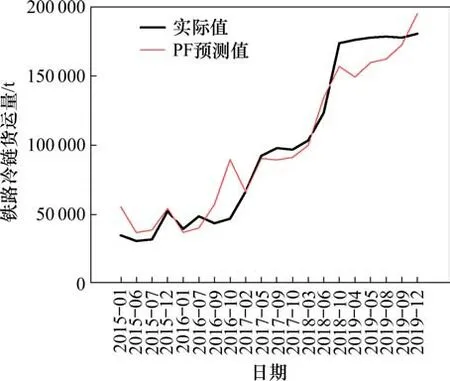
图5 预测值与实际值的对比Fig.5 Comparison between predicted value and actual value
为了验证随机森林回归预测模型在铁路冷藏运输需求预测的合理性和适用性,本文利用Bagging,AdaBoost,BP神经网络以及未进行特征筛选的随机森林(记为RF1)分别进行预测,得到训练集和测试集的MAE,MAPE,RMSE和拟合优度R2取值如表4所示。
由表4可知,训练集中各模型按照MAE排序为:AdaBoost

表4 模型预测结果对比Table 4 Comparison table of model prediction results
测试集中各模型按MAE排序为:RF
综上可知,随机森林回归预测模型的预测效果总体优于AdaBoost,Bagging和BP预测模型。基于此,利用本文构建的RF预测模型对未来3个月的铁路冷链货运量进行预测,预测结果如表5所示。

表5 RF预测结果Table 5 RFprediction results
3 结论
1)对比RF1可知,特征筛选能够提高随机森林预测模型的预测精度,由此可知,虽然铁路冷藏运输需求系统是非线性的复杂系统,且随机森林在处理高维特征具有突出优势,但并非选取的影响因素越多越好,而是需要选取重要度较高的因素,否则反而会降低随机森林模型预测精度。
2)对比Bagging,AdaBoost和BP神经网络预测模型可知,本文提出的随机森林回归预测模型的MAE和拟合优度R2均优于Bagging,AdaBoost和BP神经网络模型,MAPE和RMSE值仅高于BP神经网络,这表明随机森林预测模型在处理小样本的铁路冷藏运输需求短期预测问题上的预测效果较好。
3)对比分析训练集和测试集结果,RF和RF1模型在训练集和测试集中MAE,MAPE和RMSE值的变动范围均低于AdaBoost和Bagging模型,拟合优度R2的变动范围低于AdaBoost,Bagging和BP神经网络模型,表明随机森林回归预测模型的泛化性能较好。
4)由Spearman相关性分析结果可知,特征变量的重要程度分布较为集中,后续研究可引入权重分析。
