纳米精度在位测量系统测头误差校正方法
2022-05-17郭曦鹏王定文尹韶辉
郭曦鹏 徐 闻 王定文 李 蓉 尹韶辉
湖南大学国家高效磨削工程技术研究中心,长沙,410082
0 引言
光学非球面超精密加工过程中,光学非球面面形的加工精度受砂轮磨损、机床几何误差、环境温度变化以及机床热变形等因素综合影响,这些因素导致光学非球面面形精度降低,因此需要对光学非球面工件进行加工、在位测量、补偿加工,测量技术作为补偿加工的基础,其测量结果直接影响后续误差补偿加工效果。在位测量不仅能避免工件二次装夹误差带来的影响,还能减少辅助工时,提高加工效率,因此成为了超精密加工领域研究热点。
在位测量较为常用的有非接触光学仪器测量[1]和机械测头式测量[2]。机械测头式测量的测量原理较为简单,测量结果输出有较好的稳定性[3],但由于测头与工件直接接触,可能导致被测工件的表面划伤;采用气浮轴承的设计可以减小接触力,更适应微小结构与器件的加工,从而得到了广泛的应用。ARAI等[4]研发了一套针对非球面表面接触式测量的电容传感器在位测量装置,采用单轴进给测量,得到的结果为非球面透镜的面形,接触力小于2.3 mN,线性误差小于40 nm。
机床在位测量的过程本身可能引入新的误差,从而使测量结果偏离真实值。SHIMIZU等[5]研究了应用于卫星的大型反射镜轮廓在位测量仪补偿阿贝误差的方法,由于在位测量过程中,测头随着机床运动轴的进给而运动,机床本身几何误差的影响将反映到测头的输出。GAO等[6]设计了一种基于光学线性编码器的两轴进给在位测量装置, 并分析了机床X轴直线度误差对在位测量系统测头输出结果的影响。 LI等[7]研究了平面镜在位测量结果中包含垂直度误差在内的机床几何误差。CHEN等[8]对在位测量中沿测量轨迹进给时测头轮廓与不规则工件表面接触位置变化引起测量输出数据的偏差进行了讨论。ZHU等[9]开发了一种测量微纳结构的采用压电陶瓷驱动与电容传感器测头的在位测量系统,并采用螺旋路径测量,提高了测量效率。李昂等[10]着重分析了三坐标测量过程中根据测头球心包络面进行曲面重建生成被测表面的方法,并消除了测量坐标系与被测工件坐标系之间夹角产生的误差,但讨论的测头半径补偿为已知测头曲率半径数值的补偿,未考虑测头标称半径与测头实际半径的差距。
虽然国内外科研人员在超精密在位测量领域做了较多研究,并应用于超精密加工,然而零件的加工精度和测量精度仍难以满足预期。这是由于普遍忽视了测头形状误差对测量结果的影响。进行测头误差校正时,大多数学者只校正了测头倾斜误差或测头半径误差,而忽视了测头形状误差。虽然测头形状误差很小,但是它会直接影响测量结果,特别是在纳米精度超精密测量过程中。
本文针对接触式在位测量,建立测量数据、工件形状误差、测头形状误差三者之间的数学映射模型,利用XZ两轴联动测量标准球,实现测头形状误差辨识和校正,以某型超精密机床为对象开展了车削及测量实验。
1 测头误差校正在位测量实验装置
在位测量装置如图1所示。采用XZ两轴联动进给进行在位测量,步骤如下:
(1)测量之前,根据工件理想面形轮廓以及测头理想半径生成NC在位测量程序。
(2)测量过程中,红宝石测头与工件表面接触,接触力很小,仅有0.5 mN。Delta Tau UMAC运动控制系统按照NC轨迹设置的坐标驱动X、Z轴进给,工件实际轮廓相对于工件理想轮廓的偏差导致红宝石测头与电容传感器存在相对移动,电容传感器将记录的数据上传至UMAC运动控制系统,此相对移动可近似视为工件面形的Z向误差。
(3)测量完成后,根据被测工件理想轮廓曲线与测头中心运动轨迹曲线各点之间数学映射模型,得到被测工件的实际轮廓。
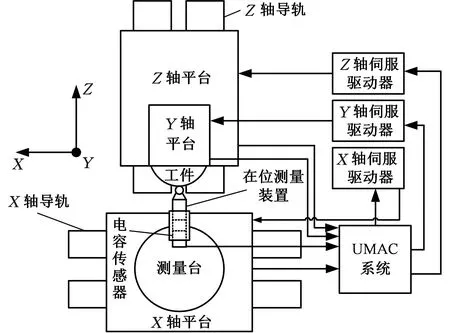
图1 在位测量装置示意图(俯视)Fig.1 Schematic diagram of on-machine measuringdevice(aerial view)
工件加工与测量过程中,机床驱动X、Z轴进给,两轴定位精度和直线度对测量准确度有较大影响。此超精密机床X轴定位精度为±0.7 nm/mm,中心处直线度为±0.7 nm/mm;机床Z轴定位精度为±0.8 nm/mm,中心处直线度为±0.7 nm/mm。由于该机床主要加工小口径非球面,X、Z轴行程分别不超过30 mm和2 mm,因此机床运动误差对测量精度的影响与测头形状误差的影响相比较小,可以忽略。
电容式传感器的量程可达20 μm至1 mm不等,频率为100 kHz时,分辨力可达量程的0.005%[11]。如图2所示,球形测头安装在方轴之上,可避免测量装置安装以及测量时球形测头发生旋转;测量过程中对气腔持续充气,保证方轴与外壳之间存在气膜,使方轴在测量过程中进行无摩擦滑动,提高测量精度。工件加工完成后,表面粗糙度Ra值通常小于10 nm,在接触力仅有0.5 mN的情况下,由摩擦力导致的测量误差很小,相较于测头导致的测量误差来说可以忽略。
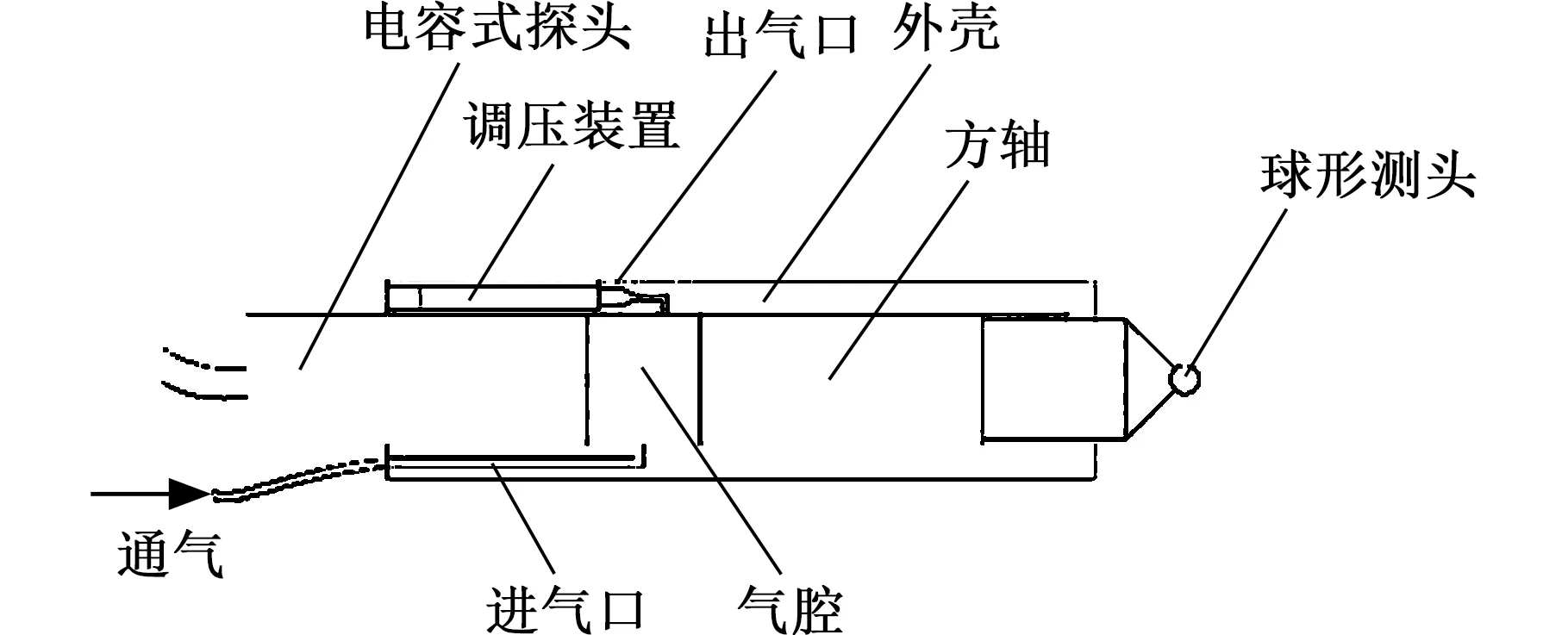
图2 电容式在位测量测头结构示意简图Fig.2 Schematic diagram of capacitive on-machinemeasure device probe
2 测头误差校正在位测量实验原理
2.1 接触式在位测量的测头误差与测量数据的关系
在两轴联动球形测头的实际测量过程中,测量数据同时受工件形状误差和测头形状误差的影响。若要使测量数据更能反映工件的实际面形轮廓,则需要讨论测量数据、工件形状误差、测头形状误差三者之间的关系,将测头形状误差的影响从测量数据中分离。
如图3所示,被测工件理想轮廓几何中心为Ow(xow,zow),测头的理想轮廓球心为Op(xop,zop),被测工件与测头两条实际不规则轮廓相切于点C(xc,zc)。C点与Ow、Op连线分别与被测工件的理想轮廓和测头理想圆弧轮廓相交于A(xa,za)、B(xb,zb)。此时工件实际轮廓误差记为
Ew=(xa-xc,za-zc)
(1)
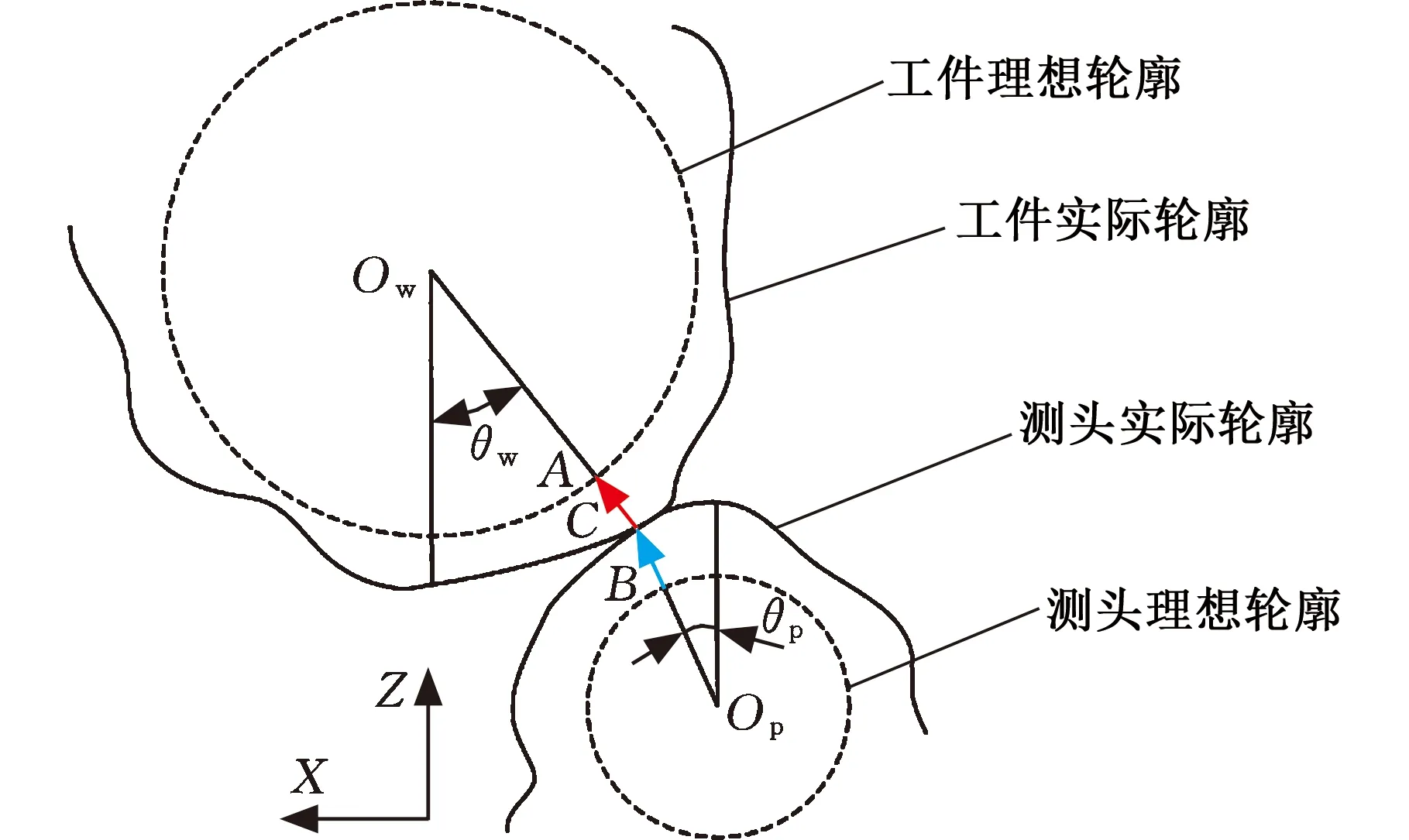
图3 被测工件表面形状误差与测头误差Fig.3 Probe error and profile error of themeasured workpiece
向量Ewp表示工件轮廓误差与测头轮廓误差综合作用导致的测量误差,存在如下关系:
(2)
(3)
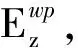
(4)
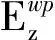
(5)

满足C点为测头实际轮廓与工件实际轮廓公切点的充要条件是:
Tw(θw)=Tp(θp)
(6)
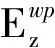
(7)
2.2 基于标准球的在位测量测头形状误差校正方法
2.2.1测头形状误差辨识
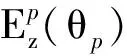
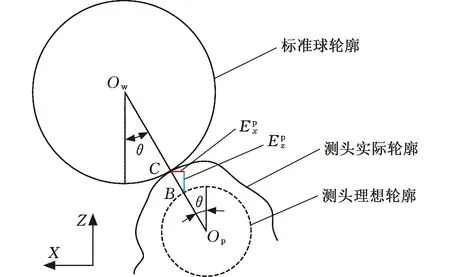
图4 使用标准球的测头形状误差校正示意图Fig.4 Schematic diagram of correcting profile errorof the probe using master ball
标准球轮廓视为理想圆弧,此时θw记为θm,存在如下关系:
Tw(θm)=tanθm
(8)
(9)
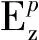
Tp(θp)≈tanθp
(10)
对于测头接触标准球时的测量,当标准球与测头的实际轮廓在点C相切时,θm、θp满足如下关系:
θm=θp
(11)
将θm、θp的值视为相等的,记作θ:
θm=θp=θ
(12)
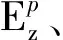
(13)
2.2.2测头形状误差校正
(14)
(15)

(16)
(17)
即
(18)
如图5所示,若根据标准球测量校正得到的测头形状正确,对工件测量NC轨迹进行测头的形状误差校正后,测头在测量轨迹上的每一点的轮廓应与工件的理想轮廓相切,理论上可消除测头形状误差带来的测量偏差。
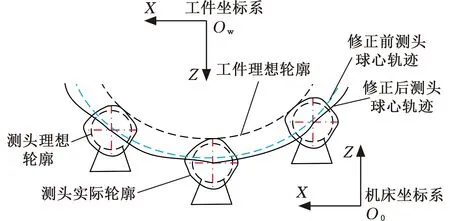
图5 工件测量NC轨迹的修正Fig.5 Correction on workpiece measuring NC routes
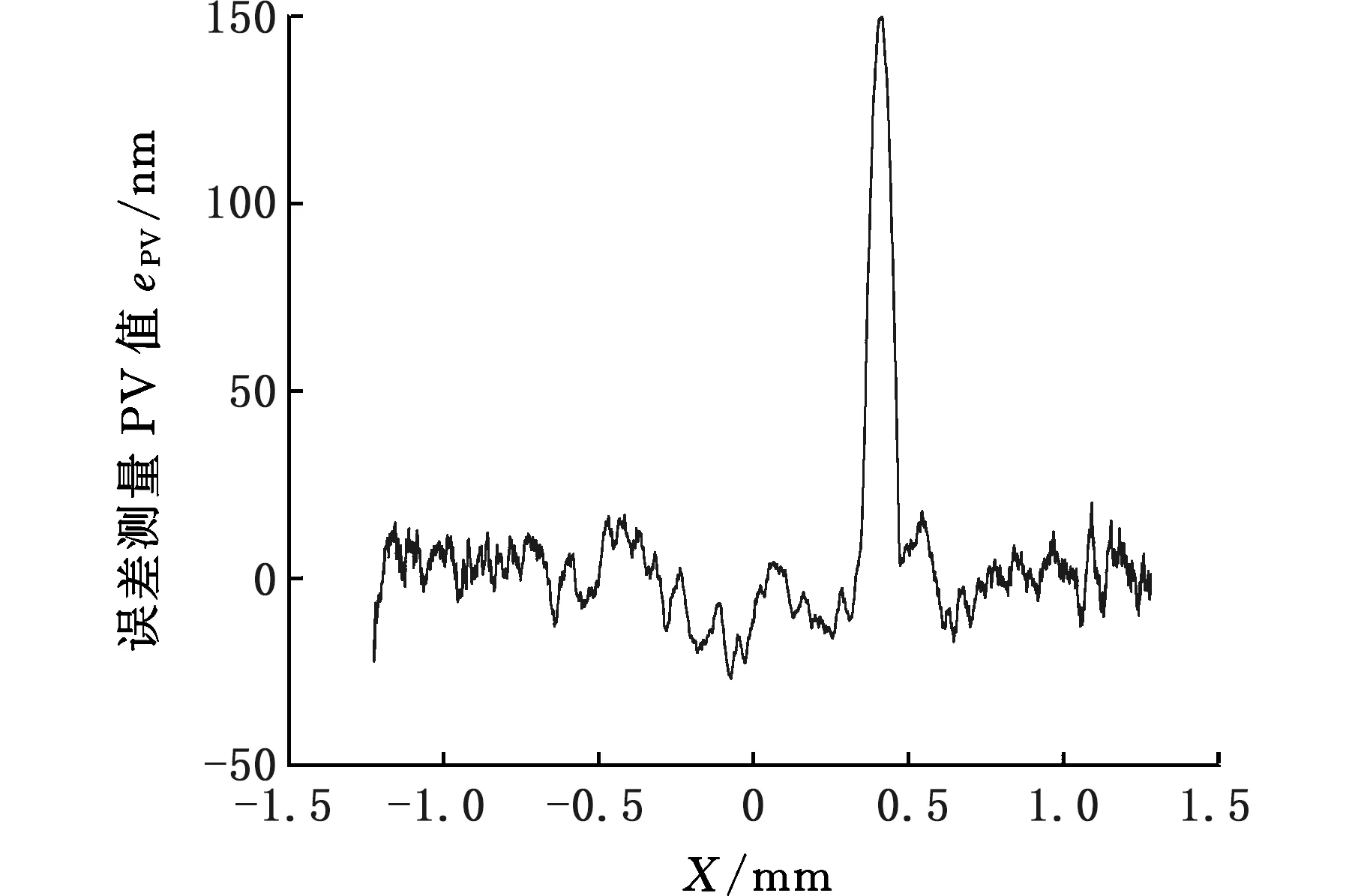
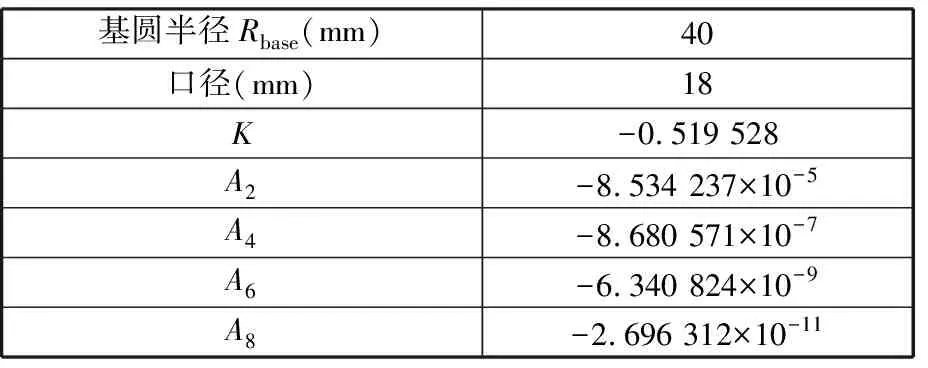
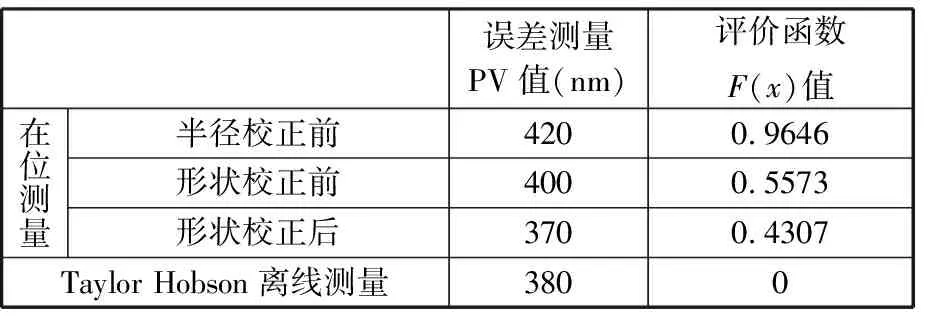
测头的误差对在位测量的影响因素除轮廓形状误差外,还有测头实际半径与测头标称半径之间的误差。测头实际半径比测头标称半径偏小或偏大时,若按照测头的标称半径生成在位测量NC轨迹,在测量对心校准的前提下,越远离工件回转轴中心部分会产生越大的测量偏差,从而影响工件整体PV值的评价标准。设Rp为生成NC测量轨迹时设定的测头半径,R为测头的实际半径,Ra (19) 图6 测头半径误差对NC测量轨迹的影响Fig.6 Influence of probe radium error on NCmeasuring routes 实验校正的测头为标称半径0.5 mm的红宝石测头。校正所用标准球直径为4 mm,实验装置如图7所示,在位测量系统参数见表1。 标准球测量实验得到的Z向输出偏差如图8a所示。图8a中X坐标为Delta Tau UMAC运动控制系统记录的测头球心经过的范围,纵坐标是与之对应的当测头球心位于该X坐标时,测头表面与标准球接触点的Z向输出偏差。将标准球表面视为被测工件表面,按照式(16)、式(19)所述的测头误差校正方法编写程序,对标准球校正测量的NC轨迹进行修正,再次依据φ4 mm标准球进行校准测量,剩余的残余误差如图8b所示,可见测头所得偏差值的大部分得以抵消。 为验证上述测头形状误差校正与测头半径误差校正方法的准确性,对基圆半径R40的非球面工件分别进行测头半径误差与形状误差校正测量,其非球面参数如表2所示,测量的X坐标区间为[-8.7,8.7]mm 。 (a)标准球校正测头形状误差 (b)工件在位测量实验图7 在位测量系统Fig.7 On-machine measurement system 表1 在位测量系统参数 (a)测头形状误差校正前(PV值为175 nm) (b)测头形状误差校正后(PV值为27 nm)图8 测头校正前后测量数据对比Fig.8 Comparison of measurement data before andafter probe correction 表2 非球面工件几何参数 采用Taylor Hobson PGI840超高精度检测仪进行离线测量,测量分辨力为0.8 nm,测量行程为8 mm,直线度为2 nm/mm。图9中1号线为Taylor Hobson离线测量结果。采用标称半径0.5 mm设定测头半径,生成NC轨迹进行测量,测量得到的误差结果如图9中2号线所示,右端存在向上凸起,与图7标准球测量结果相吻合,因此推断凸起位置为测头形状误差导致。将此结果与离线测量结果进行对比,根据式(19),分别取测量范围左侧边缘X=-8.7 mm处的偏差值进行比较,2号线在X=-8.7 mm处的偏差约为260 nm,1号线在该处偏差约为330 nm,在位测量结果的偏差值比离线测量结果的偏差值偏向正方向70 nm,可知设定测头半径0.5 mm比测头的实际半径要大,代入式(19)计算,解得ΔR为0.002 85 mm,故真实半径为0.497 15 mm。按照上述半径生成NC代码,将标准球校正测量的实验中确定的测头形状误差代入加以修正,分别采用未经测头形状误差校正的NC代码、经过测头形状误差校正的NC代码进行测量。图9中3号线为测头半径误差校正后的测量结果,图9中4号线为测头形状误差校正后的测量结果。由图9可以看出,经测头形状误差校正测量后,测头凸起位置的形状误差被校正。 为了衡量测头校正的有效性,现采用评价函数F(x)衡量测量结果与Taylor Hobson PGI840离线结果的总体接近程度。若每次测量得到的误差值为f(x),离线结果误差值为f0(x),则此次测量的评价函数为 (20) 根据式(20)评估各次在位测量结果与Taylor Hobson PGI840离线测量结果之间的符合程度,计算结果见表3。由表3可知,从被测工件校正测头误差前的测量结果,经过测头半径误差校正、测头形状误差校正两个步骤,被测工件形状误差测量结果与Taylor Hobson离线测量结果逐渐接近,可认为本文提出的测头误差校正办法是有效的。 表3 测头误差的在位测量结果校正与评估 (1)在超精密机床在位测量系统中采用两轴联动测量,测头本身的形状误差与半径误差影响被测工件形状误差测量结果。 (2)根据对测头形状误差与半径误差的理论分析,可通过以标准球为基准的测头形状误差校正以及半径误差校正修正NC测量路径,以降低两轴联动在位测量过程中半径误差的影响。 (3)按照测头半径误差校正、测头形状误差校正的顺序对工件进行校正测量,并依次记录测量得到的误差结果,与Taylor Hobson PGI840离线测量仪器测量结果比对。经测头形状误差校正测量后,测量结果由420 nm变为370 nm,与离线测量结果的380 nm的差值为10 nm。结果表明:所提测头形状误差校正方法可行,且能有效提高测量精度。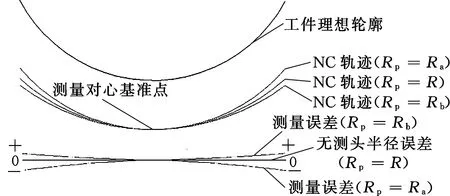
3 在位测量测头误差校正实验




4 结论
