Toeplitz算子的约化子空间研究❋

陈 熠， 石岩月

(中国海洋大学数学科学学院， 山东 青岛 266100)

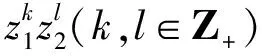
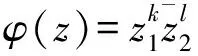
诱导的Toeplitz算子的约化子空间。此函数的解析部分和非解析部分均有变量z,w出现，不是变量可分离的，所以不能直接运用上述文献中的方法，我们的思路是结合文献[4-5,8-9]中的方法。在本文中我们沿用文献[4]中的记号，通篇均设

对任意(a,b)∈Ω，令

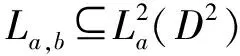
Ω1={(a,b)∈Ω|s≠t}；Ω2={(a,b)∈Ω|s=t}，

应用上述约化子空间的结论，我们还得到了Tφ生成的冯诺依曼代数的换位代数的结构。

1 预备

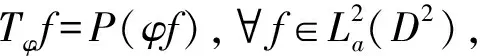
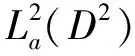
设T是Hilbert空间上的有界线性算子，M是一个闭线性子空间，若TM⊆M,T*M⊆M，则称M是T的约化子空间；若不存在T的非零的约化子空间真含于M，则称M是T的极小约化子空间。

Φ(u,n)=

(1)

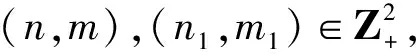
λa,b,n,m=Φ(s,n)+Φ(t,m);

Δ(n,m)={(n′,m′):(n′,m′)～a,b(n,m)}。

(2)

首先，我们给出(1)式的一些基本性质。

引理1 令Φ(x,n)如(1)式定义，其中x∈[0,1],n∈Z+，则下面结论成立：

(Ⅰ)当n≥2时，Φ(x,n)关于变量x和变量n分别严格单调递减；Φ(x,0)关于变量x严格单调递减，且Φ(x,1)关于变量x严格单调递增；

(Ⅱ)当n≥2时，Φ(x,n)-Φ(x,1)关于变量x在[0,1]上严格递减；

(Ⅲ)Φ(x,0)-Φ(x,1)关于变量x在[0,1]上严格单调递减；

(Ⅳ)Φ(x,0)<0<Φ(x,n),n≥2；

(Ⅴ)Φ(s,n)≠Φ(s,m),n,m∈Z+且n≠m；

(Ⅵ)Φ(s,x+1)-Φ(s,x)关于变量x≥2严格递增；

(Ⅶ)Φ(s,n)+Φ(t,2)>0,Φ(s,2)+Φ(t,n)>0,s,t∈(0,1]∩Q。

证明 (Ⅰ) 当n≥2时，利用下面等式容易证得结论：

当n=1时，经计算可得

当n=0时，经计算可得

(Ⅱ) 经过化简可得

f(x)=Φ(x,n)-Φ(x,1)=

从而f(x)严格递减。

(Ⅲ) 代入(1)式并化简可得

Φ(x,0)-Φ(x,1)=

从而不难验证，这个函数严格单调递减。

(Ⅳ) 根据定义可以直接验证。

(Ⅴ) 根据定义可以直接验证下列成立：

(a)若n,m≥2，由(Ⅰ)知Φ(s,n)≠Φ(s,m)。

(b)若n=0,m≥2或n≥2,m=0，由(Ⅳ)知Φ(s,n)≠Φ(s,m)。

(c)若n=0,m=1或n=1,m=0，由Φ(s,0)=Φ(s,1)得

F(s)=(s+1)2(s+2)+2s(s+2)(s+3)-

(2s+1)(s+3)(s+1)=0。

于是F是一个整系数多项式并且最高项的系数为1。从而F(s)=0的根都是整数，而

s,t∈(0,1]∩Q，且F(1)≠0。

所以Φ(s,0)≠Φ(s,1)在(0,1]上成立。

(d)若n=1,m≥2或n≥2,m=1，则有Φ(s,1)=Φ(s,m)或Φ(s,1)=Φ(s,n)。代入具体的表达式并进行化简，与上面(c)的证明类似，利用整系数多项式的性质与s∈(0,1]∩Q可得矛盾。

(Ⅵ)将(1)式代入Φ(s,x+1)-Φ(s,x)，求导即可证得。

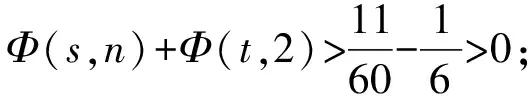
接下来，我们给出等价关系的一些基本性质。在不产生歧义的情况下，我们将(n,m)～a,b(p,q)简记为(n,m)～(p,q)。由前面给出定义知(n,p)～(m,p)当且仅当Φ(s,n)=Φ(s,m)。由引理1(Ⅰ)，于是我们容易得到下面结论。

引理2如果(a,b)∈Ω，n≠m，并且n,m≥2，那么有(n,p)(m,p),∀p∈Z+。

引理3 如果(a,b)∈Ω1并且n∈Z+(〗1}，则(n,1)(1,n)。

证明 假设(n,1)～(1,n)，则

Φ(s,n)+Φ(t,1)=Φ(s,1)+Φ(t,n)。

(3)

当n≥2时，由(3)式和引理1(Ⅱ)知s=t。当n=0时，由(3)式和引理1(Ⅲ)知s=t。这与(a,b)∈Ω1矛盾，所以(n,1)(1,n)。

记CardA为有限A中元素的个数，当A为空集时，CardA=0。下面我们对Δ(n,m)进行估计。

引理4 如果(a,b)∈Ω1，则CardΔ(0,0)≤3，且下面结论成立：

(Ⅰ)若(k,l)～(0,0)且(k,l)≠(0,0)，则

(k,l)∈{(1,1)}∪{(1,n):n≥3}∪{(n,1):n≥3}；

(Ⅱ)若CardΔ(0,0)=3，则

Δ(0,0)={(0,0),(1,m),(n,1)}，

其中n,m≥3,m≠n。

证明 根据定义容易验证

由引理1(Ⅳ)、(Ⅴ)和引理3可得下面结论：

(c) (n,1)(m,1),(1,n)(1,m),n,m∈Z+,n≠m;

(d) (1,n)(n,1),n≥2；

故我们证得所需结论。

接下来，我们考虑当(a,b)∈Ω2时等价类的性质。

引理5 如果(a,b)∈Ω2和m≠n，则

(m+1,n)(n+1,m)。

证明 假设(m+1,n)～(n+1,m)，则

Φ(s,m+1)+Φ(s,n)=Φ(s,n+1)+Φ(s,m)。

(4)

当n,m≥2时，由引理1(Ⅵ)知m=n，这与题设矛盾。当n,m满足以下情况时，

(a)n≥2,m=1；(b)n≥2,m=0；(c)n=1,m=0。

分别将(1)式代入(4)式，逐一进行化简，均可转换为首项系数为1或2的一个整系数多项式等于零的情况，利用此类多项式零点的性质以及s∈(0,1]∩Q均会产生矛盾。具体的，当首项系数为1时，s的取值只能是1，当首项系数为2时，s∈{1/2,1}，而这些数代入(4)式均不成立，所以假设不成立。

引理6 若(a,b)∈Ω2，则Δ(0,0)={(0,0)}。

证明 设(n,m)～(0,0)，则

Φ(s,n)+Φ(s,m)=Φ(s,0)+Φ(s,0)。

(5)

由引理1(Ⅳ)可知n,m必满足以下4种情况：

(Ⅰ)n≥2,m=1或m≥2,n=1；

(Ⅱ)n=1,m=1；

(Ⅲ)n=1,m=0或n=0,m=1；

(Ⅳ)n=0,m=0。

将(1)式分别按情况(Ⅰ)、(Ⅱ)和(Ⅲ)代入(5)式并进行化简，可将新等式转换为一个首项系数为1的整系数多项式Fi(s),i=1,2,3。再利用s∈(0,1]∩Q且Fi(1)≠0，以及整系数多项式零点的性质，可知(5)式无解。所以只有情况(Ⅳ)成立，即(n,m)=(0,0)。

证毕。

利用类似的方法，我们还可以得到下面结论：

引理7 若(a,b)∈Ω2，则Δ(0,1)={(0,1)，(1,0)}。

证明 显然只需证明Δ(1，0)⊆{(0,1)，(1,0)}。假设(n,m)～(1,0)且(n,m)∉{(1,0),(0,1)}。于是

Φ(s,n)+Φ(s,m)=Φ(s,0)+Φ(s,1)。

(6)

继续分情况进行讨论：

(Ⅰ)m∈{0，1}或n∈{0，1},利用引理1(Ⅴ)容易验证上面关于s的方程在(0,1]∩Q上无解。

(Ⅱ)m,n≥2，将(1)式代入(6)式并进行化简得

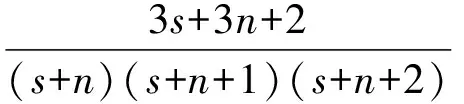
对上面等式进行通分并化简，可以转化为整系数多项式F(s)=0，且其首项系数为1。所以F(s)=0的在(0,1]上的有理根只可能为1，代入(6)式得

当n=2(或m=2)时，

当n=3(或m=3)时，m(或n)无整数解。

综上，三种情况均产生矛盾，所以假设不成立。

引理8 当(a,b)∈Ω2，n≥3时，(n,0)不在下面集合中，

{Δ(n+3,0),Δ(n+2,1),Δ(n-2,2),Δ(n+1,2),Δ(n,3),Δ(n-3,0),Δ(n-1,1)}。

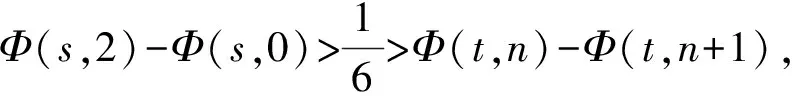
2 Tφ的约化子空间

首先，我们约定一些记号：

En=span{za+(n-r)kwb+rl:r≤n,r∈Z+};

(7)

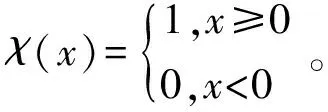
然后，给出一个后面证明中经常用到的性质。

λa,b,n,m〈Aza+nkwb+ml,za′+pkwb′+ql〉=

〈ATza+nkwb+ml,za′+pkwb′+ql〉=

〈Aza+nkwb+ml,Tza′+pkwb′+ql〉=

再由λa,b,n,m均为实数知结论成立。

接下来，我们考虑当(a,b)∈Ω1时[zawb]的性质。

定理1若(a,b)∈Ω1，则[zawb]=La,b。

证明 显然，zawb∈[zawb]。由引理3知，(1，0)(0，1)利用

可得za+kwb，zawb+l∈[zawb]，因此E1⊆[zawb]。由

可得za+2kwb-zawb+2l∈[zawb]，再由

Tφzawb=za+2kwb+zawb+2l∈[zawb]，

可得

za+2kwb，zawb+2l∈[zawb]，

从而za+kwb+l∈[zawb]，因此E2⊆[zawb]。

下面我们用数学归纳法证明Ei⊆[zawb]。假设Ei⊆[zawb](3≤i≤n)，下证En+1⊆[zawb]。

对任意0≤m≤n，由计算可知

za+(n-m+1)kwb+ml+za+(n-m)kwb+(m+1)l+

其中α=χ(n-m-2)，β=χ(m-2)。又因为

za+(n-m-2)kwb+ml,za+(n-m)kwb+(m-2)l∈En-2⊆[zawb],

所以

hm=za+(n-m+1)kwb+ml+za+(n-m)kwb+(m+1)l∈[zawb]。

进一步存在λm,λm+1∈C，使得

Thm=λmza+(n-m+1)kwb+ml+λm+1za+(n-m)k·wb+(m+1)l∈[zawb]。

若对任意1≤m≤n-1均有λm=λm+1，则

(n,1)～(n-1,2)～…～(1,n)，

这与引理3矛盾。所以至少存在一个1≤i0≤n-1，使得λi0≠λi0+1，从而

za+(n-i0+1)kwb+i0l,za+(n-i0)kwb+(i0+1)l∈[zawb],

利用hi0-1,hi0+1∈[zawb]，我们可以得到

za+(n-i0+2)kwb+(i0-1)l,za+(n-i0-1)kwb+(i0+2)l∈[zawb],

重复上述步骤，容易证得

za+(n-j+1)kwb+jl∈[zawb],0≤j≤n+1。

于是Ei⊆[zawb]。进而La,b⊆[zawb]。显然，[zawb]⊆La,b成立，所以[zawb]=La,b。

定理2若(a,b)∈Ω1，则La,b是极小的。

证明 设M⊆[zawb]为Tφ的一个约化子空间，若M⊥zawb，则M⊥[zawb]，于是M=0；若M⊥/zawb，则PMzawb≠0，由引理4和引理9，不妨设

PMzawb=a00zawb+a11za+kwb+l+

an1za+nkwb+l+a1mza+kwb+ml，

式中a00≠0，n,m≥3，n≠m且a11与an1不同时非零，且a11与a1m不同时非零。下面我将证明这些系数中只有第一项系数a00≠0，这说明zawb∈M，[zawb]⊆M，结论得证。

情况1若a11=0，则

一方面，

a00(za+kwb+zawb+l)+an1(za+(n+1)kwb+l+

za+nkwb+2l)+a1m(za+2kwb+ml+za+kwb+(m+1)l)+

b1za+(n-2)kwb+l+b2za+kwb+(m-2)l。

若an1≠0，则b1≠0。另一方面，

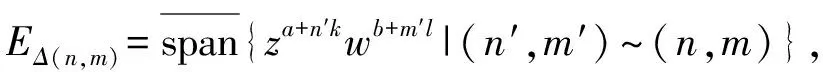
(n+1,1),(n-2,1)∈Δ(0,1)∪Δ(1,0)。

由引理1(Ⅴ)知(n+1,1)(0,1)，(n-2,1)(0,1)，所以

(n+1,1)～(1,0)，(n-2,1)～(1,0)，

这又与(n+1,1)(n-2,1)产生矛盾。于是an1=0。同理可证a1m=0。

情况2若a11≠0，由引理1(Ⅴ)知an1=a1m=0，

a00(za+kwb+zawb+l)+a11(za+2kwb+l+za+kwb+2l)∈

EΔ(0,1)∨EΔ(1,0)。

如情况1可得(2,1)～(1,0)且(1,2)～(0,1) ，即：

Φ(s,2)+Φ(t,1)=Φ(s,1)+Φ(t,0)；

Φ(s,0)+Φ(t,1)=Φ(s,1)+Φ(t,2)。

但是

Φ(s,2)-Φ(s,0)>0>Φ(t,0)-Φ(t,2),

产生矛盾。定理得证。

最后，我们考虑(a,b)∈Ω2时的性质。

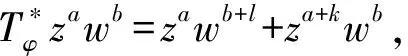
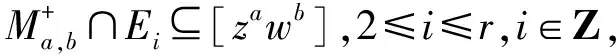
因为

za+(r-j+1)kwb+jl+za+jkwb+(r-j+1)l+

za+(r-j)kwb+(j+1)l+za+(j+1)kwb+(r-j)l+b(z,w)，

其中0≤j≤r,

(za+(r-j-2)kwb+jl+za+jkwb+(r-j-2)l)+

za+(j-2)kwb+(r-j)l)∈Er-2,

所以

za+(r-j+1)kwb+jl+za+jkwb+(r-j+1)l+

za+(r-j)kwb+(j+1)l+za+(j+1)kwb+(r-j)l∈[zawb]。

当r-j=j时，有

za+(r-j+1)kwb+jl+za+jkwb+(r-j+1)l∈[zawb]；

当r-j≠j时，由引理5，有

za+(r-j+1)kwb+jl+za+jkwb+(r-j+1)l∈[zawb]。

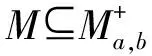
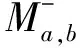
3 极小约化子空间之间的酉等价

在本节，我们考虑极小约化子空间之间的酉等价。设M1和M2为Tφ的约化子空间，若存在酉算子U:M1→M2，使得UTφ=TφU，则称M1与M2酉等价。同引理9的证明类似可得

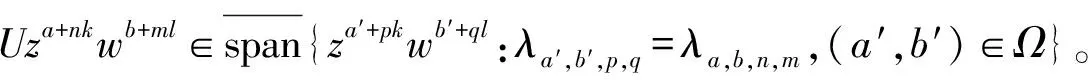
(8)

由于后面证明中将多次利用(8)式,我们需要先深入讨论算子T的特征值λa,b,n,m的性质。

引理10设(a,b),(a′,b′)∈Ω1且(s,t)≠(s′,t′),(s,t)≠(t′,s′)，则下列叙述成立：

(Ⅰ) 当λa,b,0,0=λa′,b′,0,0时，λa,b,1,0,λa,b,0,1∉{λa′,b′,1,0,λa′,b′,0,1}；

(Ⅱ) 当λa,b,n,1=λa′,b′,0,0，n≥2时，λa,b,n,0∉{λa′,b′,2,0,λa′,b′,0,2}；

(Ⅲ) 当λa,b,n,0=λa′,b′,0,0，n≥2时，λa,b,n,1∉{λa′,b′,1,0,λa′,b′,0,1}；

(Ⅳ)λa,b,0,0∉{λa′,b′,2,0,λa′,b′,0,2}。

证明 (Ⅰ)假设λa,b,1,0=λa′,b′,1,0，由于λa,b,0,0=λa′,b′,0,0，于是分别代入(2)式并且两式相减可得

Φ(s,1)-Φ(s,0)=Φ(s′,1)-Φ(s′,0)，

由引理1(Ⅲ)可得s=s′，代入

Φ(s,0)+Φ(t,0)=Φ(s′,0)+Φ(t′,0)

可得Φ(t,0)=Φ(t′,0)，由引理1(Ⅰ)可得t=t′，矛盾。类似可证λa,b,0,1≠λa′,b′,0,1,λa,b,0,1≠λa′,b′,1,0,λa,b,1,0≠λa′,b′,0,1。

(Ⅲ)假设λa,b,n,1=λa′,b′,1,0，由于λa,b,n,0=λa′,b′,0,0，于是分别代入(2)式并且两式相减可得

Φ(t,1)-Φ(t,0)=Φ(s′,1)-Φ(s′,0)，

由引理1(Ⅲ)可得t=s′，代入

Φ(s,n)+Φ(t,0)=Φ(s′,0)+Φ(t′,0)，

得Φ(s,n)=Φ(t′,0)，然而Φ(s,n)>0,Φ(t′,0)<0，矛盾。

类似可证λa,b,n,1≠λa′,b′,0,1。

(Ⅳ)由引理1(Ⅶ)和(Ⅳ)有λa′,b′,2,0>0,λa′,b′,0,2>0，λa,b,0,0<0，所以λa,b,0,0∉{λa′,b′,2,0,λa′,b′,0,2}。

引理11设(a,b),(a′,b′)∈Ω2，则下列叙述成立：

(Ⅰ)当λa′,b′,0,0=λa,b,1,1时，λa′,b′,2,0≠λa,b,1,0；

(Ⅱ) 当λa,b,0,1=λa′,b′,0,0时，λa,b,0,0∉{λa′,b′,2,0,λa′,b′,0,2}；

(Ⅲ)λa,b,0,0=λa′,b′,0,0当且仅当(a,b)=(a′,b′)。

证明 (Ⅰ)、(Ⅱ)证明方法与引理10(Ⅱ)类似。

(Ⅲ) 因为(a,b),(a′,b′)∈Ω2，λa,b,0,0=λa′,b′,0,0，代入(2)式可得Φ(s,0)=Φ(s′,0)，由引理1(Ⅰ)可得s=s′，因此(a,b)=(a′,b′)。

引理12设(a′,b′)∈Ω1,(a,b)∈Ω2，n≥2，则下列叙述成立：

(Ⅰ) 当λa′,b′,0,0=λa,b,1,1时，λa,b,1,0∉{λa′,b′,2,0,λa′,b′,0,2}；

(Ⅱ) 当λa′,b′,0,0=λa,b,n,1时，λa,b,n,0∉{λa′,b′,2,0,λa′,b′,0,2}；

(Ⅲ)当λa′,b′,0,0=λa,b,0,0时，λa,b,0,1∉{λa′,b′,1,0,λa′,b′,0,1}。

证明 (Ⅰ)和(Ⅱ)证明方法与引理10(Ⅱ)类似。(Ⅲ)证明方法与引理10(Ⅰ)类似，最后可得s′=t′，从而矛盾。

引理13设(a,b)∈Ω2，则下列叙述成立：

(Ⅰ)当n>m≥3时，(n+1,m)∉{Δ(n-2,m),Δ(n,m-2)}，(n,m-2)∉{Δ(n-2,m),Δ(n,m+1)}；

(Ⅱ)当n≥2,m=1时，(n+1,1)∉{Δ(n-2,1),Δ(n,2)}，(n,2)(n-2,1)；

(Ⅲ)当n≥2,m=0时(n+1,0)∉{Δ(n-2,0),Δ(n,1)}，(n-2,0)(n,1)。

证明 这里只证明当n≥4时(n,m-2)(n-2,m)，可通过求导的方法得出当n≥4时f(x)=Φ(x,n-2)-Φ(x,n)在x∈[0,1]上严格递减，所以若(n,m-2)～(n-2,m)，则n=m，矛盾。其余结论可结合引理1，或者利用首项系数为1或2的整系数多项式零点的性质以及s∈(0,1]∩Q证得。

命题1当(a,b),(a′,b′)∈Ω1且(a,b)≠(a′,b′)时，La,b与La′,b′酉等价当且仅当(s,t)=(t′,s′)。

证明 充分性：若 (s,t)=(t′,s′)，如下定义

U:La,b→La′,b′,Uza+nkwb+ml=za′+mkwb′+nl。

可以验证U是一个酉算子，并且

UTφza+nkwb+ml=

TφUza+nkwb+ml。

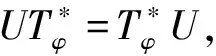
必要性：设(s,t)≠(t′,s′)，若存在满足条件的酉算子U：La,b→La′,b′，只需证明

Uza+nkwb+ml⊥za′wb′,n,m∈Z+。

(9)

这与U是满射矛盾。于是命题得证。

当n,m≥2时，由引理1(Ⅳ)知λa,b,n,m>0>λa′,b′,0,0，由(8)式得(9)式成立。接下来我们考虑当n∈{0,1}或m∈{0,1}时的情况。假设(9)式不成立，同上有λa,b,n,m=λa′,b′,0,0。由引理4，不妨设

Uza+nkwb+ml=c0za′wb′+c1za′+kwb′+l+

c2za′+pkwb′+l+c3za′+kwb′+ql,

(10)

其中c0≠0,p,q≥3且c1,c2不同时非零，c1,c3不同时非零。进一步计算得

za+nkwb+l)=c0(za′+kwb′+za′wb′+l)+g(z,w)，

(11)

其中g(z,w)⊥{za′+kwb′,za′wb′+l}。

断言1Uza+nkwb⊥za′wb′,n=0,1。

否则，由引理9知λa,b,n,0=λa′,b′,0,0。

当n=0时，由引理10(Ⅰ)知λa′,b′,1,0∉{λa,b,1,0,λa,b,0,1}，因此〈Uza+kwb,za′+kwb′〉=〈Uzawb+l,za′+kwb′〉=0，从而(11)式的左边与za′+kwb′的内积为零，但是其右边

〈c0(za′+kwb′+za′wb′+l)+g(z,w)，za′+kwb′〉≠0，

产生矛盾。

当n=1时，由假设得λa′,b′,0,0=λa,b,1,0，再由(10)式得

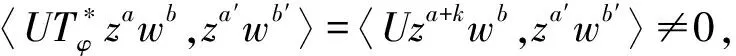
〈Uzawb,za′+2kwb′+za′wb′+2l〉,

所以λa,b,0,0∈{λa′,b′,0,2,λa′,b′,2,0}，这与引理10(Ⅳ)矛盾。

利用对称性可证Uzawb+l⊥za′wb′。

断言2Uza+nkwb⊥za′wb′,n≥2。

否则，我们有λa′,b′,0,0=λa,b,n,0。由引理1(Ⅶ)知n≥3。由引理10(Ⅲ)知

λa′,b′,1,0≠λa,b,n,1，λa′,b′,0,1≠λa,b,n,1。

所以Uza+nkwb+l⊥{za′+kwb′,za′wb′+l}。由(11)式得

c0〈za′+kwb′+za′wb′+l,h(z,w)〉，

(12)

其中h(z,w)∈{za′+kwb′,za′wb′+l}。同上分析得到

{λa′,b′,0,1,λa′,b′,1,0}={λa,b,n+1,0,λa,b,n-2,0}。

若λa′,b′,1,0=λa,b,n-2,0，由(12)式得

〈Uza+(n-2)kwb,za′+kwb′〉=

引理1(Ⅴ),(Ⅶ)表明(n,0)(n-3,0)，λa,b,n-2,2>0>λa′,b′,0,0，于是

〈UTφza+(n-2)kwb,za′wb′〉=

〈Uza+nkwb,za′wb′〉=c0||za′wb′||2。

同时

〈TφUza+(n-2)kwb,za′wb′〉=

〈Uza+(n-2)kwb,za′+kwb′+za′wb′+l〉=

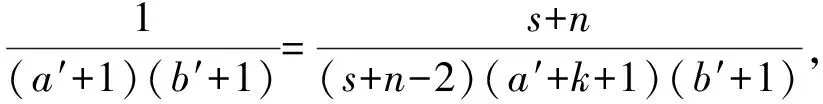
n-2=2s′-s<2。

于是我们有n=3，2s′-s=1，λa′,b′,1,0=λa,b,1,0和λa′,b′,0,0=λa,b,3,0。但0<Φ(s,3)-Φ(s′,0)=Φ(s,1)-Φ(s′,1)。由f(x)=Φ(x,1)严格单调增知s>s′，从而容易验证s=2s-s>2s′-s>1，这与2s′-s=1矛盾。同理当λa′,b′,0,1=λa,b,n-2,0时也产生矛盾。

利用引理10(Ⅲ)的对称性得到当λa,b,0,n=λa′,b′,0,0时，λa,b,1,n∉{λa′,b′,0,1,λa′,b′,1,0},n≥2。再利用断言1和断言2的方法，类似的可以得到下面结论，这里不再叙述细节。

Uzawb+nl⊥za′wb′,U*za′wb′+nl⊥zawb,n≥0。

(13)

断言3Uza+kwb+l⊥za′wb′。

否则，λa′,b′,0,0=λa,b,1,1。一方面由引理1(Ⅶ)得

〈U(zawb+2l+za+kwb+l),za′wb′〉=

〈Uza+kwb+l,za′wb′〉≠0，

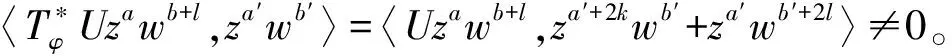
〈Uza+kwb,za′+2kwb′+za′wb′+2l〉≠0。

当λa′,b′,0,2=λa,b,0,1，λa′,b′,2,0=λa,b,1,0时，

〈Uza+kwb,za′+2kwb′〉≠0。

由断言2得

〈Uzawb,za′+4kwb′〉=〈zawb,U*za′+4kwb′〉= 0，

同理由断言1得〈Uzawb,za′+kwb′〉=0，又因为λa,b,2,2>0>λa′,b′,0,0，所以〈Uzawb,za′+2kwb′+2l〉=0，进而

产生矛盾。

利用轮换性，当λa′,b′,2,0=λa,b,0,1，λa′,b′,0,2=λa,b,1,0时，同样也会产生矛盾。断言3得证。

断言4Uza+nkwb+l⊥za′wb′,n≥2。

否则，我们有λa′,b′,0,0=λa,b,n,1，再结合断言1,2可得

〈Uza+nkwb,za′+2kwb′+za′wb′+2l〉 =

〈Uza+nkwb+l,za′wb′〉≠0，

所以λa,b,n,0∈{λa′,b′,2,0,λa′,b′,0,2}，但这与引理10(Ⅱ)矛盾。

可利用引理10(Ⅱ)的对称性得到当λa,b,1,m=λa′,b′,0,0时，λa,b,0,m∉{λa′,b′,0,2,λa′,b′,2,0}，类似断言4的方法，可证得Uza+kwb+ml⊥za′wb′,m≥3。

综上， 当n<2或m<2时，(9)式成立，命题得证。

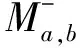
U(za+nkwb+ml-za+mkwb+nl)⊥(za′+kwb′-za′wb′+l),n>m≥0。

(14)

由引理7和引理9，不妨设

U(za+nkwb+ml-za+mlwb+nl)=c0(za′+kwb′-za′wb′+l),c0≠0,

则

U(f1(z,w)+f2(z,w)+f3(z,w)+f4(z,w))=

c0(za′+2kwb′-za′wb′+2l)，

(15)

其中

f1(z,w)=za+(n+1)kwb+ml-za+mkwb+(n+1)l,

f2(z,w)=za+nkwb+(m+1)l-za+(m+1)kwb+nl,

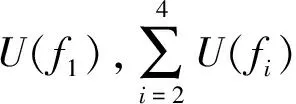
(Ⅱ) 当n=1,m=0时，利用引理7，计算可得

其中

γ=〈U(za+kwb-zawb+l),za′+kwb′-za′wb′+l〉。

于是

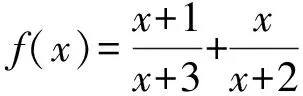
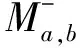
U(za+nkwb+ml-za+mkwb+nl)⊥za′wb′,n>m≥0。

(16)

由引理6和引理9，假设

U(za+nkwb+ml-za+mkwb+nl)=c0za′wb′,c0≠0。

情况1当n>m≥2时，λa,b,n,m>0>λa′,b′,0,0，这与λa,b,n,m=λa′,b′,0,0矛盾。

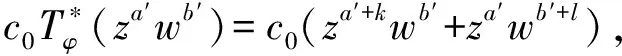
情况3当n=1,m=0时，结合引理6和引理7得

γ=〈U(za+kwb-zawb+l),za′wb′〉。

再结合λa,b,1,0=λa′,b′,0,0可得方程组

经过化简得2s3+10s2+13s+1=0，然而当s∈(0,1]时，2s3+10s2+13s+1=s(2s2+10s+13)+1>1，产生矛盾。(16)式得证。

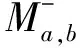
U(za+nkwb+ml-za+mkwb+nl)=

c0za′wb′+c1za′+kwb′+l+c2za′+qkwb′+l+c3za′+kwb′+pl，

其中c0≠0,p,q≥3且c1,c2不同时非零，c1,c3不同时非零。

情况1当n>m≥2或n=2,m∈{0,1}时，

λa,b,n,m>0>λa′,b′,0,0，

这与λa,b,n,m=λa′,b′,0,0矛盾。

情况2当n>2,m=0时，由引理1(Ⅴ)，(Ⅶ)知

λa′,b′,0,0∉{λa′,b′,3,0,λa′,b′,2,1,λa′,b′,1,2,λa′,b′,0,3}，

再利用引理8和下面等式

(17)

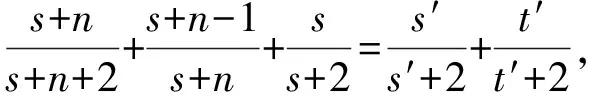
产生矛盾。

情况3当n=1,m=0，则

c0(za′+kwb′+za′wb′+l)+f(z,w),

其中f(z,w)⊥{za′+kwb′,za′wb′+l}，于是λa′,b′,0,1=λa′,b′,1,0=λa,b,2,0，这与引理3矛盾。

情况4当n>2,m=1时，λa′,b′,0,0=λa,b,n,1。结合情况2和3的结论可得：

〈U(za+nkwb+l-za+kwb+nl),za′wb′〉=

〈U(za+nkwb-zawb+nl),za′+2kwb′+za′wb′+2l〉，

则λa′,b′,0,2=λa,b,n,0或λa′,b′,2,0=λa,b,n,0，这与引理3(Ⅱ)矛盾。

综上，式(16)成立，命题得证。

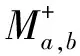
U(za+nkwb+ml+za+mkwb+nl)⊥za′wb′,n≥m≥0。

(18)

显然，由引理1(Ⅰ)，(Ⅳ)，(Ⅶ)和引理11(Ⅲ)知，当n≥m≥2时或n=m=0或2∈{n,m}时，λa,b,n,m≠λa′,b′,0,0。其他情况时，假设

U(za+nkwb+ml+za+mkwb+nl)=c0za′wb′,c0≠0。

注意到，当n>2,m∈{0,1}时，将(15)式左边的减号换成加号，(15)式右边换成c0(za′+kwb′+za′wb′+l)，利用引理13(Ⅱ),(Ⅲ)，与命题2的证明一致。于是为证明本命题，我们只需证明当n,m∈{0,1}时结论也成立。

情况1当n=m=1时，λa′,b′,0,0=λa,b,1,1，且λa,b,2,0>0>λa′,b′,0,0

可得

2〈Uza+kwb+l,za′wb′〉=

〈U(za+kwb+zawb+l),za′+2kwb′+za′wb′+2l〉≠0,

(19)

所以λa,b,1,0=λa′,b′,2,0，与引理11(Ⅰ)矛盾。

情况2当n=1,m=0时，因为

〈U(zawb+l+za+kwb),za′wb′〉=

〈Uzawb,za′+2kwb′+za′wb′+2l〉≠0，

所以λa′,b′,2,0=λa,b,0,0，与λa′,b′,2,0>0>λa,b,0,0矛盾。

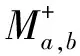
U(za+nkwb+ml+za+mkwb+nl)=

c0za′wb′+c1za′+kwb′+l+c2za′+qkwb′+l+c3za′+kwb′+pl,

其中c0≠0,p,q≥3且c1,c2不同时非零，c1,c3不同时非零。

情况1当n=m=1时，λa′,b′,0,0=λa,b,1,1。同样由(19)式知λa,b,1,0∈{λa′,b′,2,0,λa′,b′,0,2}，这与引理12(Ⅰ)矛盾。

情况2当n>2,m=0时，将命题4的情况2中(17)式的减号换成加号，证明过程一致。

情况3当n=m=0时，则λa′,b′,0,0=λa,b,0,0，结合引理1(Ⅶ)和情况2的结论，我们有：

〈UTφ(za+kwb+zawb+l),za′wb′〉=

〈U(za+kwb+zawb+l),za′+kwb′+za′wb′+l〉，

所以λa′,b′,1,0=λa,b,0,1或λa′,b′,0,1=λa,b,0,1，与引理12(Ⅲ)矛盾。

情况4当n=1,m=0时，因为

〈U(zawb+l+za+kwb),za′wb′〉=

〈Uzawb，za′+2kwb′+za′wb′+2l〉，

所以λa,b,0,0∈{λa′,b′,2,0，λa′,b′,0,2}，这与下列不等式矛盾

λa′,b′,2,0>0,λa′,b′,0,2>0,λa,b,0,0<0。

情况5当n>2,m=1时，λa′,b′,0,0=λa,b,n,1，结合情况1～4的结论可得

〈U(za+nkwb+l+za+kwb+nl),za′wb′〉=

〈U(za+nkwb+zawb+nl),za′+2kwb′+za′wb′+2l〉,

有λa′,b′,0,2=λa,b,n,0或λa′,b′,2,0=λa,b,n,0。与引理12(Ⅱ)矛盾。

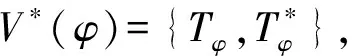
a=m1k′-1,b=m2l′-1,a′=m2k′-1,

b′=m1l′-1,

其中σ=GCD(k,l),k=k′σ,l=l′σ,m1,m2∈[1,σ],m1≠m2。利用文献[4]中的方法，我们可以得到下面定理：

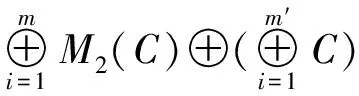
*-同构，其中m=(σ2-σ)/2,m′=kl-σ2+2σ。