冲刷地形下近壁面串列双圆管绕流问题的数值模拟❋
2022-05-17鲁小辉梁丙臣
鲁小辉, 张 嶔, 杨 博, 梁丙臣,3
(1. 中国石油化工集团有限公司安全监管部, 北京 100728;2. 中国海洋大学工程学院, 山东 青岛 266100;3. 中国海洋大学山东省海洋工程重点实验室, 山东 青岛 266100)
在海洋、海岸工程的实际应用中,海洋结构物中的圆管状结构物通常成对出现[1],如平行布置的海底输油管线等结构。然而当水流经过这些成对的结构物时会因为存在尾迹干扰而使流动更为复杂。当水流流经一对平行布置的圆管时,上游圆管产生的尾涡会和下游的圆管相互作用,并且两圆管的尾迹受制于两管的间距影响,从而产生延伸体流态、重新附着流态以及共同脱落流态等复杂的流态[2]。当两管之间的间距较近时,下游圆柱处在上游圆柱的尾涡形成区域,同时从上游圆柱表而分离的剪切层会完全包围下游圆柱,且剪切层在卷曲产生Karman涡之前不会附着在下游圆柱表面,此时尾迹处于延伸体流态。随着两管之间的间距增大,从上游圆柱分离的剪切层会重新附着到下游的圆柱上,此时尾迹处于重新附着流态。而当两管之间的间距进一步增大时,两圆柱的尾迹都出现Karman涡脱落,此时尾迹表现为共同涡脱落流态。上述不同间距条件下的流态特征同样还受到入流雷诺数等因素的影响[3]。
迄今为止,众多学者对于不受壁面影响下的串列双圆管绕流的特征开展过实验研究[3-5]。绝大多数的实验研究集中于104量级的雷诺数区间内。在数值模拟方面,Meneghini等[6]利用分数步法模拟了雷诺数在100~200之间的双圆管流场相互作用及涡脱落特性。刘松和符松[7]、郭晓玲等[8]、涂佳黄等[9]利用直接数值模拟方法研究了低雷诺数下串列双圆管的流场及涡激振动特征。Uzun和Yousuff Hussaini[10], Gopalan和Jaiman[11], 赵伟文和万德成[12]利用RANS和LES混合的方法模拟了雷诺数为1.66×105条件下不同间距的串列双圆管流场特征。
对于近壁面条件下的串列双圆管绕流的研究目前开展较少,目前多集中于对水平壁面影响下的流场研究。Harichandan和Roy[13],Bhattacharyya和Dhinakaran[14]开展数值模拟研究,探究了较低雷诺数条件下的近壁面串列双圆管流场特征。Prsic等[15]利用大涡模拟技术研究了在雷诺数为1.31×104条件下,两管间距分别为2和5倍管径,竖直方向距离水平壁面均为1倍管径的串列双圆管绕流场特征。Li[1]在Prsic等[15]的基础上进一步探究了不同竖直方向间距对流场特征的影响。然而对于冲刷地形下的串列双圆管流场,Zhao等[16]基于RANS模型对不同圆管间距条件下的冲刷过程开展二维数值模拟,探究了水平间距对冲刷深度及水动力特征的影响。但是目前对于冲刷地形下串列双圆管的三维水动力精细化数值模拟研究方面较为匮乏。因此本文采用Spalart-Allmaras改进延迟分离涡模拟(Improved delayed detached eddy simulation,IDDES)以更深入地研究在不同间距及不同冲刷地形条件下串列双圆管的流场特征,该模型对边界层内的流动采用雷诺平均方法,对边界层外的流动采用大涡模拟方法,在节省计算资源的同时可以精确模拟湍流的分离,因此可以更深入地分析圆管周围流场特性。
1 数学模型
1.1 基本方程
对于不可压缩黏性流体,在直角坐标系下,其运动规律可以用Navier-Stokes方程来描述,连续性方程和动量方程分别为
(1)
(2)
式中:ui为速度矢量;xi为笛卡尔坐标系;i=1,2,3;j=1,2,3;ρ为流体密度;p为压力;t为时间;v为流体的运动黏滞系数。
基于RANS理论,流场中任一点速度及压力可以分解为:
(3)

(4)

将方程和方程带入方程和方程中可得:
(5)
(6)
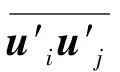
1.2 Spalart-Allmaras DES-IDDES模型
混合模型的诞生主要是为弥补RANS在捕捉流场细节方面的不足,同时混合模型还减少LES较大的计算量。Spalart等[17]在1997年首次提出了一种混合RANS/LES的分离涡(Detached eddy simulation,DES)模型,该模型通过单一湍流模型来实现对三维非定常流动的精确模拟,在网格密度满足大涡模拟要求的区域应用LES模型,在壁面附近网格密度满足RANS要求的区域应用标准的Spalart-Allmaras湍流模型[18]来解雷诺平均Navior-Storkes方程,从而大幅减少计算时间[19]。
在构造RANS/LES混合模型时,需要对方程中的耗散项进行转换,方法是构造一个开关函数。RANS/LES的转换则通过引入长度尺度来判别。DES方法的长度尺度被定义为:
dDES=min(d,ψCDESδ)。
(7)
式中:d为与壁面最近的距离;CDES经验常数,建议取值为0.65;ψ为低雷诺数校正函数[20];δ为网格尺度。
在壁面附近,d≪ψCDESδ时,采用Spalart-Allmaras湍流模型[17]进行计算;与ψCDESδ≪d时,采用亚网格模型进行计算。
但是当网格密度介于LES模型与RANS模型要求之间时,DES模型不能捕捉全部的流场紊动,模拟的涡流黏性与雷诺应力均将减小,即模拟应力耗尽现象(Modeled stress depletion, MSD)[20]。为了解决由网格密度引起的近壁面处模拟应力耗尽的问题,Spalart等[20]在标准分离涡模拟(Detached eddy simulation,DES)模型的基础上开发了延迟分离涡模拟(Delayed detached eddy simulation,DDES)模型。DDES模型通过涡流黏性检测边界层的位置,并强制边界层内的流场由RANS方法求解。
DDES方法长度尺度为:
dDDES=d-fdmax(0,d-ψCDESδ)。
(8)
式中fd为基于经验公式的遮蔽函数[20]。在LES区域(rd≪1)时,fd=1,DDES模型即为DES模型;在其余区域fd=0。
Spalart-Allmaras IDDES模型是由Shur等[21]基于DDES和WMLES(Wall modeled LES)改进的RANS/LES混合模型。WMLES模型在边界层内部区域使用雷诺平均方法,在外部使用大涡模拟,但在RANS和LES模型切换区域存在偏差。IDDES模型解决了该问题,该模型将计算域分成三类子域,分别为远离壁面区域、近壁面区域、二者之间区域。当入流条件中没有湍流时,IDDES模型中的DDES方法就会被激活。当入流条件中有湍流且网格密度精细到足够覆盖边界层内的涡时,IDDES模型中的WMLES方法就会被激活。RANS和LES两种方法通过以下公式结合在一起:
dIDDES=fB(1+fe)dRANS+(1-fB)dLES。
(9)
式中:dRANS=d;dLES=ψCDESδ;fB和fe为经验函数[21]。
2 计算模型
2.1 计算域及边界条件设置
本文依据Zhang[22]在西澳大学的大型环形水槽中开展的串列双圆管浑水冲刷试验,本文依照其试验的流场及冲刷稳定后的地形剖面数据建立三维数值水槽,探究不同间距条件下的双圆管局部流场特征。计算域如图1所示,计算区域的长度(x方向)、宽度(z方向)和高度(y方向)分别设置为60D、4D和11D,其中D为圆管直径。两个平行的圆柱分别放置于对应间距地形的冲刷坑中,G1和G2分别为两个圆管正下方冲刷坑深度,上游圆管1的中心位于距入流边界(xMin)10D处,下游圆管2中心位于距离入流边界11D+L处,L为2个圆管之间的间距。在两管不同间距的条件下,下游圆管2中心到出流边界的距离最小为44D,最大为49D。这保证了两圆管下游尾流的充分发展。

图1 计算域示意图Fig.1 Schematic of the computational domain
计算域左侧为入流边界,其入流流速剖面利用相同的求解程序在一个未放置圆管的平整底面计算域中生成。该边界层入流的生成方法已经成功的应用于对冲刷地形下单圆管流场的模拟研究中,并取得了良好的效果(1)曲孟祥, 杨博, 梁丙臣, 等. 基于IDDES方法的冲刷地形海底管道绕流数值模拟[J]. 海洋工程 (待发表).。计算域右侧(xMax)边界为自由出流边界,流速ui及压力p均采用零梯度边界条件。圆柱壁面和计算域底部边界(yMin)为无滑移壁面边界,即流速ui=0, 压力p为零梯度边界条件。计算域顶部(yMin)距离圆管足够远,因此在顶部应用钢盖假定和忽略了对自由液面变化的模拟。计算域前(zMin)、后(zMax)边界均采用周期性边界条件。计算域及流场参数如表1所示。
2.2 地形剖面及网格
图2给出了不同L/D条件下冲刷地形剖面及计算网格。由图2中可以发现,在L/D≤1.0时,仅在双圆管下方形成了一个单一的冲刷坑,其深度随L/D的增大而增大。当L/D>1时,在两个圆管之间形成了一个较小的沙丘,沙丘的尺度随着L/D的增大而增大。

表1 入流流场参数及计算域几何特征Table 1 Parameters of the flow field and geometric characteristics of the calculation domain
在L/D=4.9时,计算网格采用非结构化六面体网格;在L/D≠4.9时,计算网格均采用结构化六面体网格。这是因为在L/D=4.9采用结构化网格较难满足对于网格非正交性的要求,从而容易导致计算发散。为保证计算的精度,所有计算网格均对圆管周围及床面附近的网格进行了加密(见图1)。
表2中列出了每个算例的网格数、近管道壁面及近床面区域的网格厚度。所有结构化网格算例的网格总数在2 000万左右,而非结构化网格总数略少,约为1 380万。在近管道壁面及近床面区域,垂直壁面方向上第一层网格最大厚度均为0.002D,以保证y+值均在1左右。这些网格参数已在先前的研究中证明满足IDDES模拟要求的经度①。
3 计算结果与分析
3.1 力系数分析
图3给出了在不同L/D的条件下,上、下游圆管的阻力系数CD和升力系数CL的变化图。阻力系数CD和升力系数CL定义为:
(10)
(11)
式中:FD和FL分别代表单位长度圆管所受到的水平和竖直方向的作用力;um为实验来流流速。

(横坐标代表无量纲水平距离,纵坐标代表无量纲竖直距离。The horizontal coordinates represent the dimensionless horizontal distance and the vertical coordinates represent the dimensionless vertical distance)

表2 模型网格参数Table 2 Mesh parameters
由图3可以发现,随着L/D的增大,上游圆管的阻力系数略有减小,但其平均值变化不大。随着L/D的增大,上游圆管的升力系数逐渐变为负数,虽然当L/D较大时,瞬时升力系数会大于0,但其平均值仍为负值。这一点与Li[1]的结果不同,在水平壁面条件下串列双圆柱的受力升力系数始终趋近于0。这表明在冲刷地形下,上游圆管会受到一个流场施加的向下的作用力,将上游圆管推向冲刷坑的方向,这更有益于上游管线处于稳定状态[16]。对于在L/D较小时,下游圆管阻力系数始终为负值,这表明其受到了流场施加的一个推力。随着L/D的增大,下游圆管的阻力系数逐渐变为正值。
从两个圆管的升力系数的变化过程可以发现,在L/D=0.0时,上、下游圆管的升力系数的波动保持着相同的频率,这说明两个圆管的尾迹流态属于延伸体流动模式,即两个圆柱体组合成一个单一绕流结构[23]。而当L/D=0.5或L/D=1.0时,上游圆管的升力波动频率相对于下游圆管明显减弱,这说明两圆管的尾轨模式发生转换,由上游圆管分离的尾涡受到下游圆管的影响而被抑制。随着L/D的进一步增大,上游圆管的升力波动逐渐增加,并且与下游圆管保持近似的频率,这表明两圆管的尾轨进入共同脱落模式。由于在本研究中入流的雷诺数较大,尾轨模式发生转换时的L/D值会明显缩小,这也符合先前的研究成果[3]。
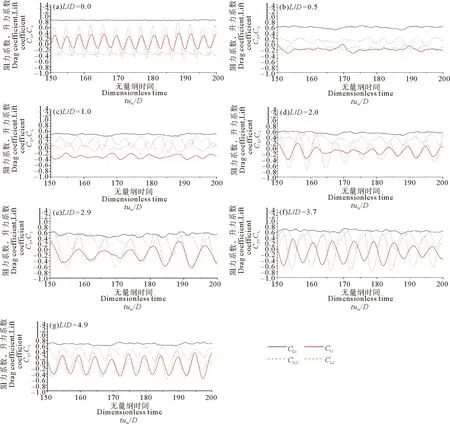
图3 不同L/D条件下,上、下游圆管力系数变化Fig.3 Variation of the force coefficients under different L/D conditions
3.2 时均流场分析
图4给出了在不同L/D的条件下的时间平均流线及压力云图。从中可以发现,在L/D=0.0时,从上游圆管分离的流线完全包络了下游的圆管,并且在圆管下游形成了较小的尾轨回流区。在L/D=0.5时,可以明显的看到从上游圆管分离的尾涡连续的附着在了下游管线的表面,且在两个圆管之间形成一个涡对[24]。这表明圆管的尾迹流态进入了重新附着模式,也进一步验证了图3中上游圆管的升力发生变化的原因。此时受到两管之间涡对的影响,从上游圆管分离的流线包络范围略微增大。且两管之间的下部涡旋迫使流线进一步向下偏移,从而使冲刷坑的范围逐渐增大。当L/D=1.0时,从上游圆管分离的尾涡依然附着在下游管线的表面,但是此时上部涡旋逐渐消失,而下部涡旋的范围逐渐增大,形成一个类似方箱流动的流场。类似的现象同样存在于Li[1]对水平壁面附近的串列双圆柱的流场模拟中。该涡旋具有更大的尺度与表面曲率,使得圆管下部的流线进一步向下偏移,从而增大冲刷坑的深度,但冲刷坑的水平尺度略有减小。随着L/D的进一步增大两圆管的尾轨进入共同脱落模式,从时均压力场变化可以发现,下游圆管的迎流面的压强逐渐增大,这说明上游圆管的尾流对下游圆管的影响逐渐减小。从时均流线变化可以看出,两个圆管后部逐渐形成了近乎对称的回流区,且下部的回流区涡旋相对于上部更强。由图2中受力变化可知,上述过程中伴随着强烈的尾涡脱落。
3.3 瞬态涡量场分析
图5给出了不同L/D条件下瞬时涡量等值面图,所选取的涡量的等值面为8.0,其中颜色条代表沿着x方向的瞬时速度。从图5中可以发现,当L/D=0时,在双圆柱后方形成了一个单一脱落的尾涡,且形成了较为明显的肋部涡结构。随着L/D的增大,尾涡结构逐渐变得复杂。但是在L/D≤1时,从圆柱分离的尾涡几乎不与圆柱下方的床面发生直接的相互作用,说明此时冲刷坑的发展主要受制于平均流场的影响。而当L/D=2时,可以清楚的发现从上游圆管脱落的尾涡冲击了下游圆管下方的床面,从而增大了下游圆管下方的冲刷坑的深度,导致了在两管之间形成了较陡的沙丘。随着L/D的进一步增大,从上游圆管脱落的尾涡与下游床面相互作用的位置逐渐变化,从而影响了两管之间沙丘的位置与形态。当L/D=4.9时,此时上游圆管尾涡在未到达下游圆管之前发生耗散,从而减弱了下游圆管对下方冲刷坑的影响。使得两管之间沙丘的水平尺度和堆积高度不断的增高,呈现出与单管冲刷类似的地形特征。
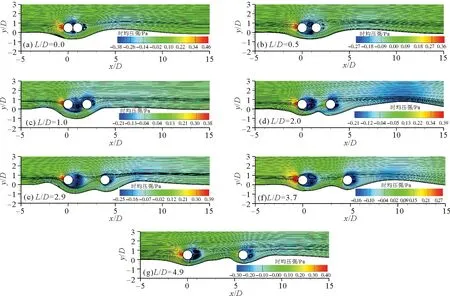
(时均压强:Time-averaged pressure. 位于z=2D切面处,横坐标代表无量纲水平距离,纵坐标代表无量纲竖直距离。Located at z=2D, the horizontal coordinates represent the dimensionless horizontal distance and the vertical coordinates represent the dimensionless vertical distance.)
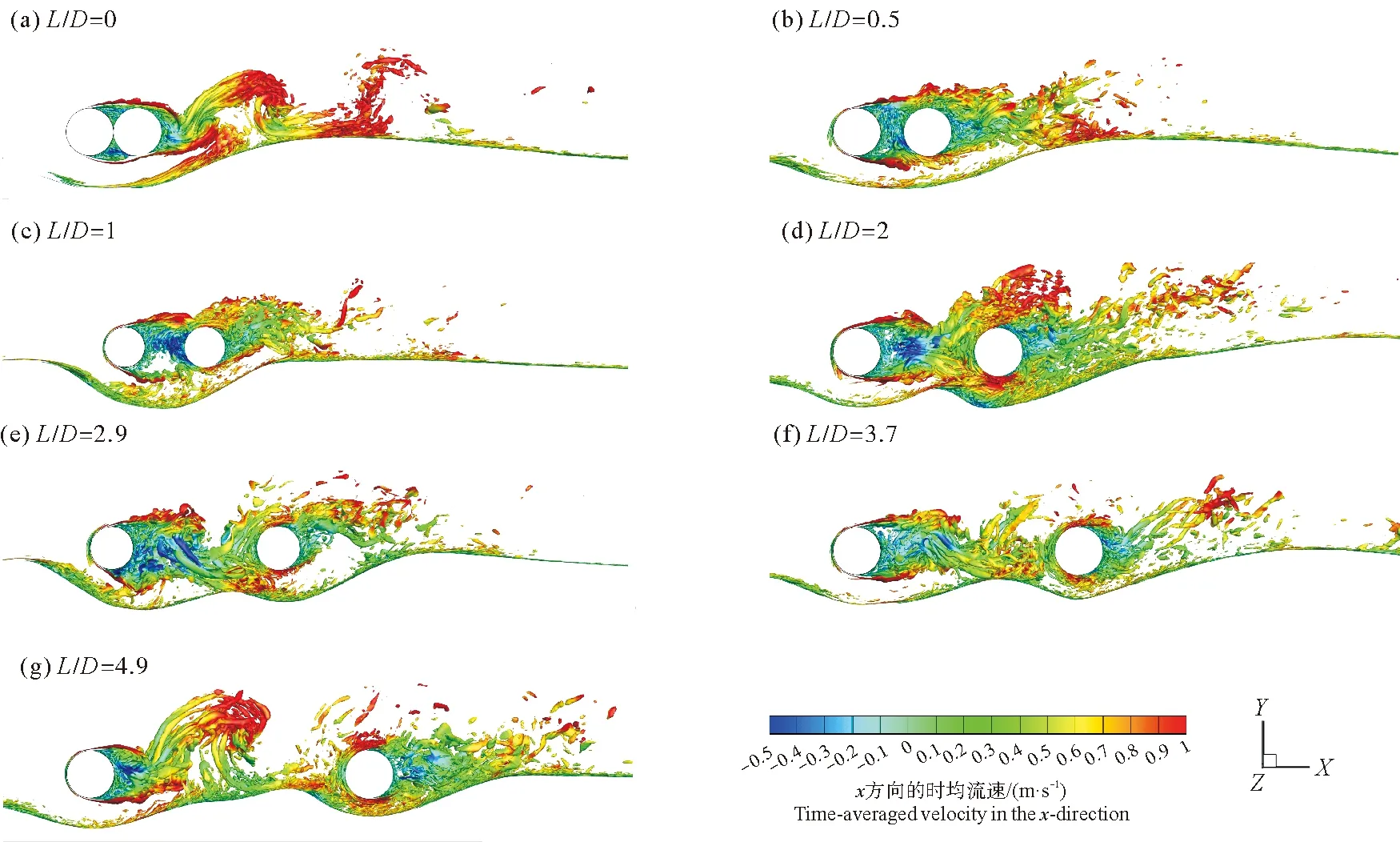
(等值面为8.0,位于z = 2D切面处。Iso-surface=8.0,Located at z=2D.)图5 不同L/D条件下瞬时涡量等值面Fig.5 Iso-surface of instantaneous vorticity for different L/D conditions
4 结论
(1)随着L/D的增大,上游圆管的升力系数逐渐变为负数。而下游圆管的阻力系数在L/D较小时为负值,并且当L/D>1时突然转为正值。上游圆管的涡脱落频率在重新附着模式下会出现明显的减弱。
(2)在L/D≤1时,圆管上面的分离涡对圆管下方床面影响较小,圆管下方的冲刷主要受制于平均水流的影响。且两管之间涡旋随着L/D的增大而增大,这进一步影响了平均流场与冲刷坑的特征。
(3)在L/D≥2时,两圆管的尾迹表现为共同涡脱落流态,此时上游圆柱的尾涡将会对下游圆柱的冲刷产生较大的影响,从而在两管之间形成沙丘。
