澳大利亚某金矿矿化域模型资源量估算及参数优化

杜菊民，祖辅平，景永波，陈 诚，陈 峰，蔡卫东

(1.江苏省地质工程有限公司，江苏 南京 210018； 2.西安石油大学地球科学与工程学院，陕西 西安 710065； 3.江苏省地质勘查技术院，江苏 南京 210049； 4.江苏省矿产勘查局第一地质大队，江苏 南京 210018)

随着地质统计学与计算机科学的发展，三维地质建模已在资源量估算、成矿预测等领域得到广泛应用[1-3]。国内受到传统地质勘查规范的约束[4]，通常采用边界品位、工业品位的双指标来建立矿体三维模型，并进行资源量估算[5-6]。以工业双指标体系圈定矿体的方式属于硬边界处理，割裂了地质数据的空间相关性[7]，不仅影响了三维资源量估算工作的效率及矿床成矿预测的准确性[8-10]，还阻碍了动态资源量估算，掩盖了三维软件估值的优势[11]。目前国际社会普遍采用低于边界品位的矿化域指标进行资源量估算，即软边界处理方式[7]。实践证明，采用矿化域指标对斑岩型、热液蚀变型等矿床进行资源量估算，不仅在边界品位动态优化、工业指标论证时，能大幅提高工作效率[9,12]，而且更能客观反映矿化规律，有利于进行成矿预测[8,13]。随着《资源量估算规程》(DZ/T 0338—2020)的发布，采用矿化域模型进行资源量估算必将得到更广泛的应用。

澳大利亚某金矿成矿类型为与侵入岩相关型，总体品位偏低,矿岩界线呈过渡关系，因此，可先用相对低的品位圈连出完整性较好的矿化域，再采用矿块指标体系圈定矿体范围。本次研究在地质统计的基础上，对矿化域品位边界值、特异值、理论变异函数、搜索椭球体等关键参数进行了优化设置，以普通克里格法进行了资源量估算，并对估值结果进行全局验证。本文对相关资源量估算工作具有一定参考作用。

1 矿床地质特征

澳大利亚拉克兰造山带(Lachlan Orogen)为典型的大陆边缘增生造山带，由西带、中带和东带三个亚带组成[14]。本文研究的金矿位于拉克兰造山带中带，矿体赋存于晚古生代细粒二长闪长岩株中，该岩株侵入至早古生代强烈褶皱变形的石英片岩。主要蚀变类型包括：硅化、绢云母化、钠长石化、黄铁矿化、毒砂化等，围绕细粒二长闪长岩株蚀变晕分带明显，在该岩株外侧还发育局部角岩化蚀变带。矿体呈筒状，直径约160 m，垂直往下延伸近1 000 m。矿化以金为主，砷含量较高，为低品位大型金矿。

2 数据库建立与样品基本统计

2.1 钻孔数据库的建立

钻孔数据库是进行三维地质解译、品位估值的基础。本文基于3DMine三维矿业工程软件平台技术要求，提取钻孔定位数据表、测斜数据表、样品分析数据表、地质岩性表等，建立钻孔数据库。经数据纠错、完整性和逻辑性检查后，用于后期样品统计和地质建模工作。钻孔数据根据需要进行显示，以方便后续地质解译(图1)。矿体由54个钻孔控制，孔深18.0～1 312.6 m，总进尺12 091 m，采样6 364件，样长1～3 m。

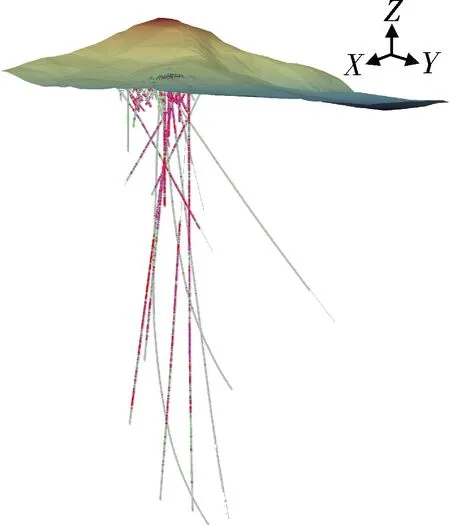
图1 澳大利亚某金矿地表及钻孔三维效果图Fig.1 3D renderings of surface and boreholes of a gold mine in Australia

2.2 原始样品基本统计

提取所有原始样品点进行基本分析。从原始样品品位分布直方图及分布曲线来看，样品呈正偏态分布(图2(a))，经对数处理后，矿化部分样品服从正态分布，因此可以采用地质统计法进行资源量估算。 原始样品中大于金检出限样品共5 808件，最小值0.01 g/t，最大值59.4 g/t。 其中，平均值(0.806 98 g/t)与西舍尔估值(1.282 06 g/t)偏差过大，偏度(25.267 01)也较大(表1)，说明需进行特异值处理。

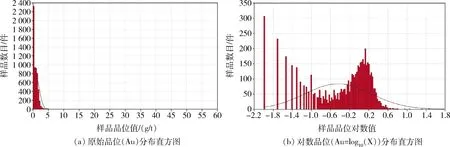
图2 原始样品品位分布直方图Fig.2 Histogram of original sample grade distribution

表1 不同类型样品基本统计信息Table 1 Basic statistical information of different types of samples

2.3 矿化域品位边界值的确定

原始样品品位值对数处理后，品位对数值-0.6～-0.8之间的样品数量分布存在明显拐点(图2(b))。对品位对数值进行分布区间比例统计，结果见表2。由表2可知，在对数值为-0.744 7时，样品占比为30.0%，对应原始样品品位为0.19 g/t，即大于等于0.19 g/t的样品占样品总数的70.0%，代表了拐点后的样品矿化较为连续。因此，本文采用0.19 g/t作为矿化域品位边界值。

3 矿化域模型的构建

3.1 矿化域实体模型

实体模型又称矿体的表面模型或线框模型，由封闭的三角网组成，可以进行体积估值、三维显示等[15]。先根据矿化域品位边界值圈定大致连续的矿化范围，再采用样条曲线对矿化域边界进行平滑与渐变处理[11,13]，使实体模型更接近自然实际情况。建立的矿化域模型见图3(a)。

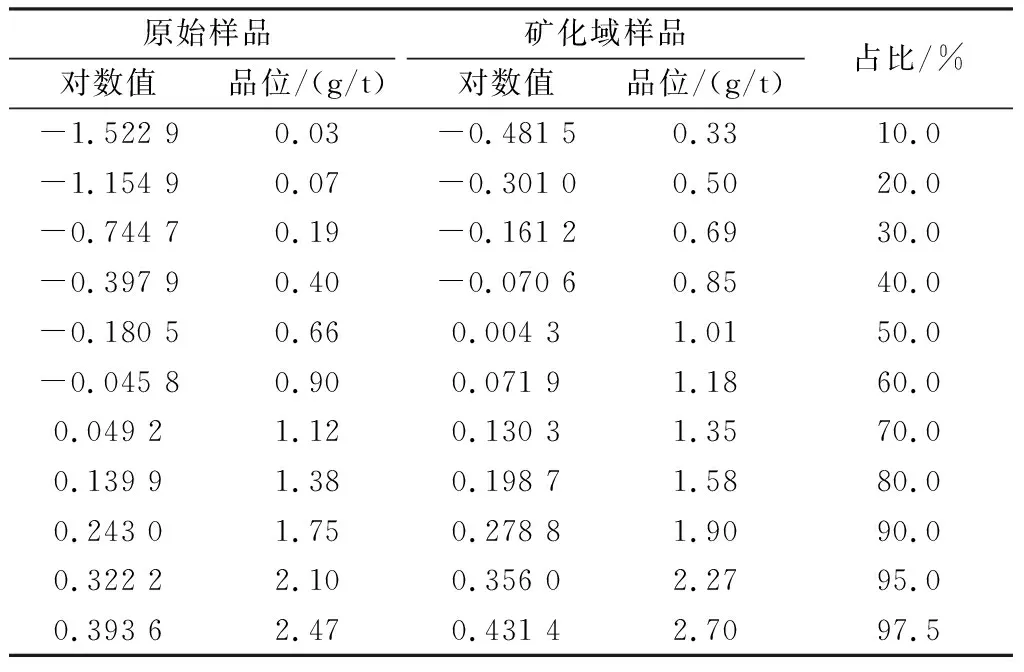
表2 原始样品及矿化域样品品位分布Table 2 Grade distribution of original samples and mineralized domain samples

3.2 矿化域块体模型

实体模型内部为空值，无法进行空间品位、体重、矿岩类型等属性赋值或估值，需按矿化域走向、倾向等因素，确定基本块体规格，创建块体模型。矿化域实体边缘设置次级块体，以精细模拟矿化域边界。基本块体规格一般设为工程间距的1/4～1/5，次级矿体规格一般设为基本块体的1/2或1/4。基本块体太大无法显示品位变化，块太小可导致品位估值不可靠。本次工作根据矿化域模型形态及钻孔间距，将矿化域基本块体规格设置为4 m×4 m×10 m，次级块体设置为1.0 m×1.0 m×2.5 m。矿化域块体模型见图3(b)。

4 特异值处理及合理性检验

4.1 特异值的识别与处理

特异值是指特高品位和特低品位，在品位估值中通常指特高品位。由于其超过了期望的品位分布范围，对品位均值、方差等造成较大影响，会引起品位高估[16]。采用普通克里格法进行估值，进行变异函数分析及特异值处理时，应以矿化域或矿体为单位进行。特异值的识别与处理有多种方法，本文选择分布衰减或不连续的点作为特高品位。

利用矿化域实体模型提取矿化域样品进行基本分析，共提取4 052件样品，最小值0.19 g/t，最大值59.4 g/t。其中平均值(1.130 05 g/t)与西舍尔估值(1.135 87 g/t)接近，但偏度(27.556 02)较大(表1)，说明存在特高品位。

对矿化域样品分别绘制原始品位与对数品位分布直方图(图4)。 由图4(a)可知，在品位大于5 g/t之后样品数量大幅减少。 由图4(b)可知，品位对数值在0.66附近出现不连续，此时样品品位为4.57 g/t。因此，本文将4.57 g/t作为特高品位下限进行替换处理，共替换12件样品。

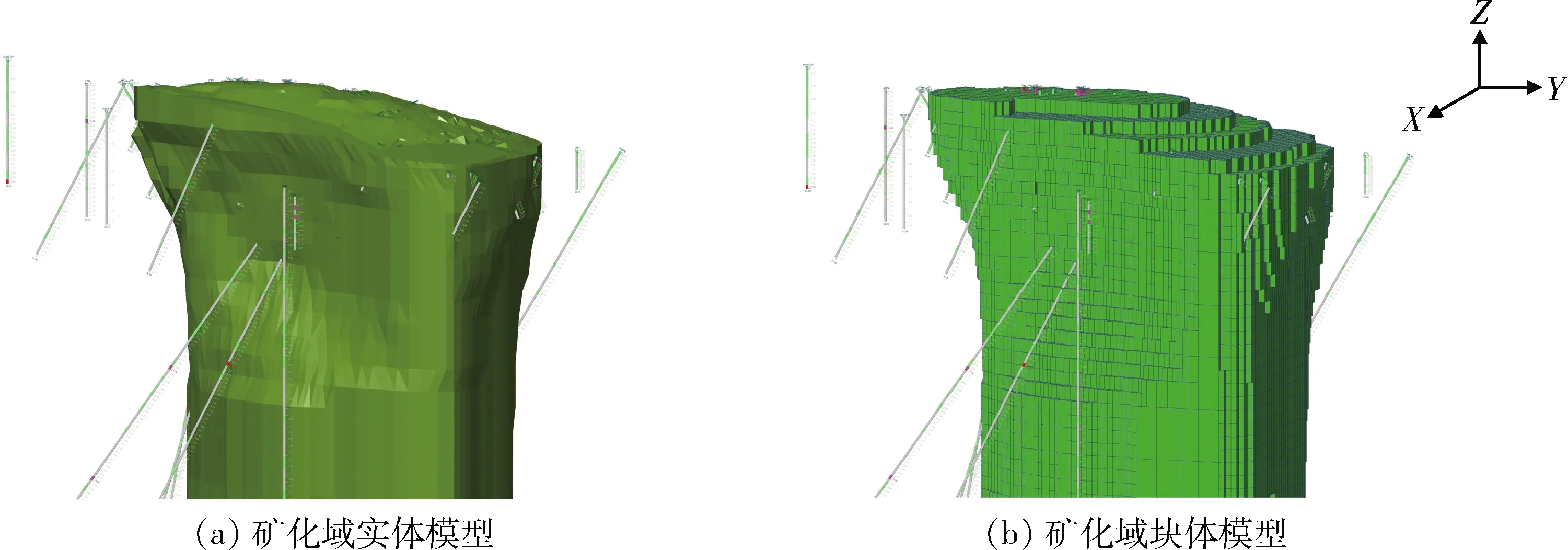
图3 矿化域实体及块体模型(局部)示意图Fig.3 Part of 3D mineralized domain entity model and block model of gold deposit

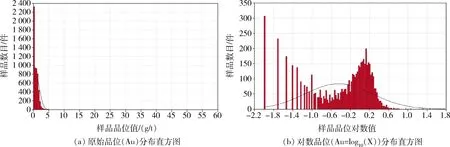
图4 矿化域样品品位分布直方图Fig.4 Histogram of sample grade distribution in mineralized domain

4.2 特异值的空间分布

确定特高品位值后，需观察特高品位样品在空间的位置，如空间距离很近且分布有规律，则需将高品位样带单独圈出进行资源量估算，而不作为特高品位样品处理[16]。经统计与观察，12件特高品位样品三维空间分布零散，不具备单独划分高品位矿体域的条件。

4.3 特异值处理后的检查

采用西舍尔估值进行合理性检验，处理特异值后样品的算术平均值小于且与西舍尔估值接近时，表明特异值处理合理。 对处理完特异值的样品数据进行基本统计，算术平均值(1.101 92 g/t)小于且与西舍尔估值(1.127 36 g/t)接近，偏度(1.357 51)相对特异值处理前大幅减少，变异系数(0.611 31)进一步减少(表1)，说明处理后样品接近正态分布，矿化相对均匀。因此，以品位4.57 g/t为下限进行特异值处理取值合理。

5 样品组合与变异函数分析

5.1 样品组合

样品组合是将空间上长度不等的样品量化到等长的离散点，以保证参数统计的无偏估计[6,15,17]。 对处理特异值后矿化域样品进行样长统计，样长集中在1 m、2 m和3 m，平均1.7 m(图5)，所以本次以2 m作为样品组合长度，最小样品长度选择1 m。 样品等长组合后，共生成3 435件组合样。与处理特异值后矿化域样品相比，组合样品的平均值(1.093 62 g/t)与西舍尔估值(1.118 07 g/t)更为接近(表1)。

图5 矿化域样品样长直方图Fig.5 Sample length histogram of mineralized domain samples

5.2 变异函数拟合

变异函数是地质统计学中研究样品空间分布随机性和结构性的主要工具。使用块金值(C0)代表样品变化的随机成分，基台值(C)代表样品变化的相关成分，变程(R)代表相关性存在的最大范围。样品的相关性与矿种、成矿类型、样品采集等因素有关。

对组合后的样品进行变异函数分析，根据样品空间分布位置，设置16个扇区，进行主轴变异函数分析，依次确定主轴、次轴和短轴的实验变异函数；采用球状模型理论变异函数，通过调整块金值、基台与变程对实验变异函数进行拟合。本次工作拟合了三套参数进行交叉验证，从中优选出最合理的变异函数模型参数，各套模型参数详见表3。

5.3 变异函数交叉验证

使用构建的变异函数对已知样品点进行估值，比较估计值和真值的差值，并进行差值统计分析，交叉验证块金值、基台和变程的合理性。真值与估计值的误差均值趋近于“0”，误差方差与克里格估计方差比值趋近于“1”，为交叉验证的理想结果[15]。

基于以上思路，分别对三套理论变异函数参数，设置主轴搜索半径范围在10 m至200 m之间，开展交叉验证对比， 验证结果生成折线图(图6)。 随着主轴搜索半径的增大，结果显示如下几方面特征：①三套参数的误差均值快速增加，并趋于平稳；②误差方差与克里格估计方差比值增加至峰值后，缓慢回落；③参数一在主轴搜索半径设置为50 m时，真值与估计值的误差均值为0.010 1，误差方差与克里格估计方差比值为0.927 2；④参数二在主轴搜索半径设置为80 m时，误差均值为0.010 2，方差比值为0.895 6；⑤参数三在主轴搜索半径设置为70 m时，误差均值为0.009 7，方差比值为0.999 6。

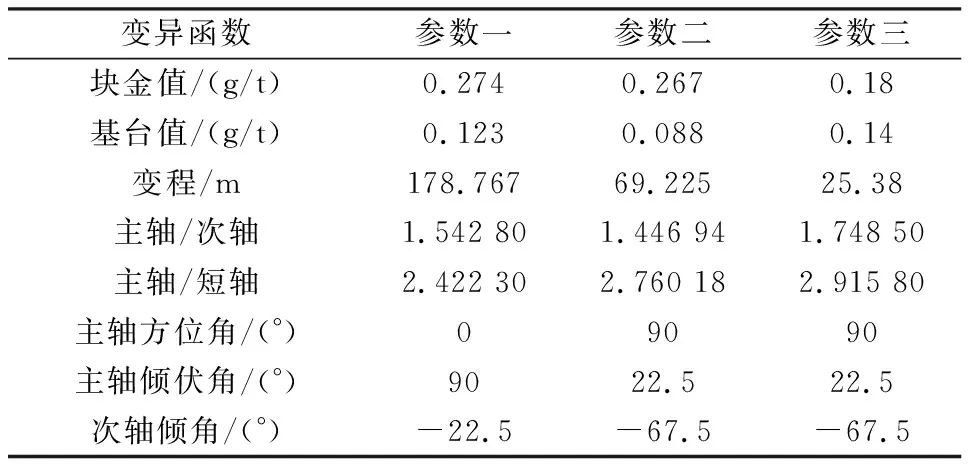
表3 理论变异函数参数组合Table 3 Combinations of theoretical variogram parameters

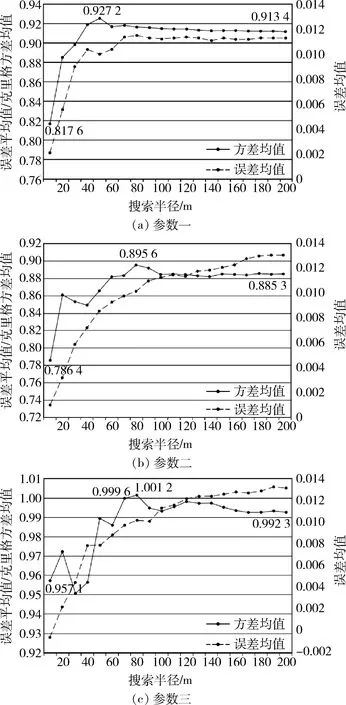
图6 不同参数交叉验证结果统计Fig.6 Statistics of cross-validation results of different parameters

对比三套理论变异函数交叉验证结果(图6)，采用参数三时，具有最趋近于“0”的误差均值，以及最趋近于“1”的误差方差与克里格估计方差比值。因此，参数三是最为合理的理论变异函数参数，参数三的主轴、次轴及短轴方向变异函数见图7。

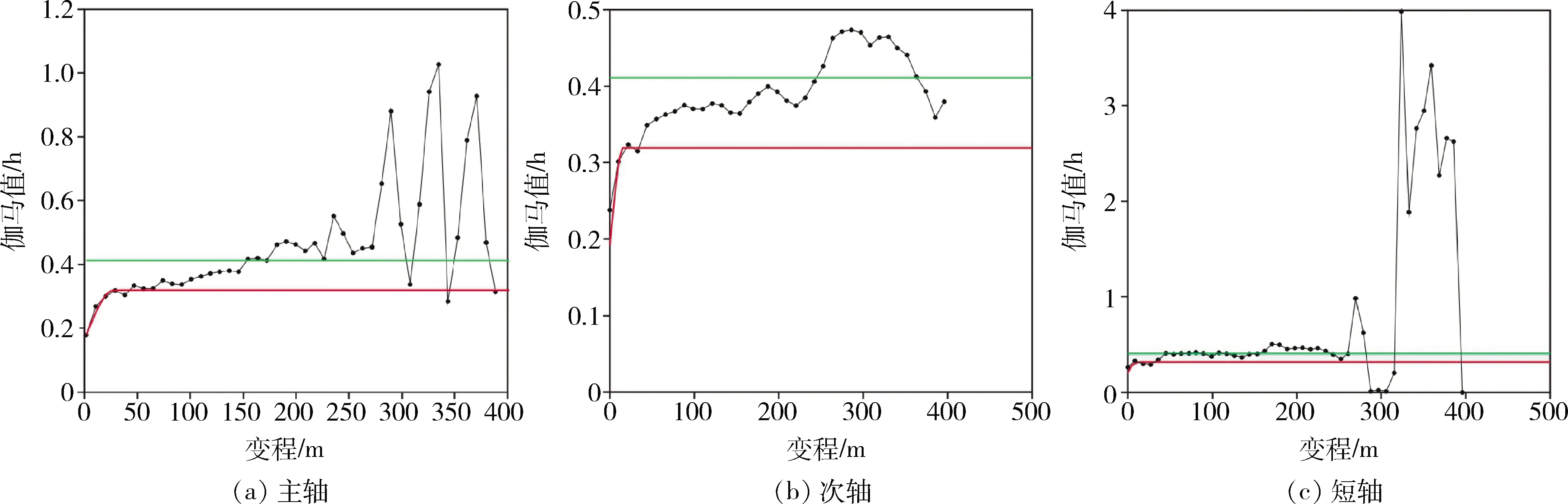
图7 参数三主轴、次轴及短轴方向变异函数示意图Fig.7 Schematic diagram of the variation function from major axis,minor axis and minor axis of the parameter three

6 资源量估值、验证及分类

6.1 普通克里格估值

根据矿体特征、工程分布及变异函数(参数三)，确定本次普通克里格估值参数(表4)，对块体模型的Au品位属性进行估值。主轴搜索半径参考勘探工程间距及变程，设置为25 m及其偶数倍。最少样品数、最多样品数及每孔最多选择样品数的设置可以减弱样品数据的丛聚效应，提高估值精度。

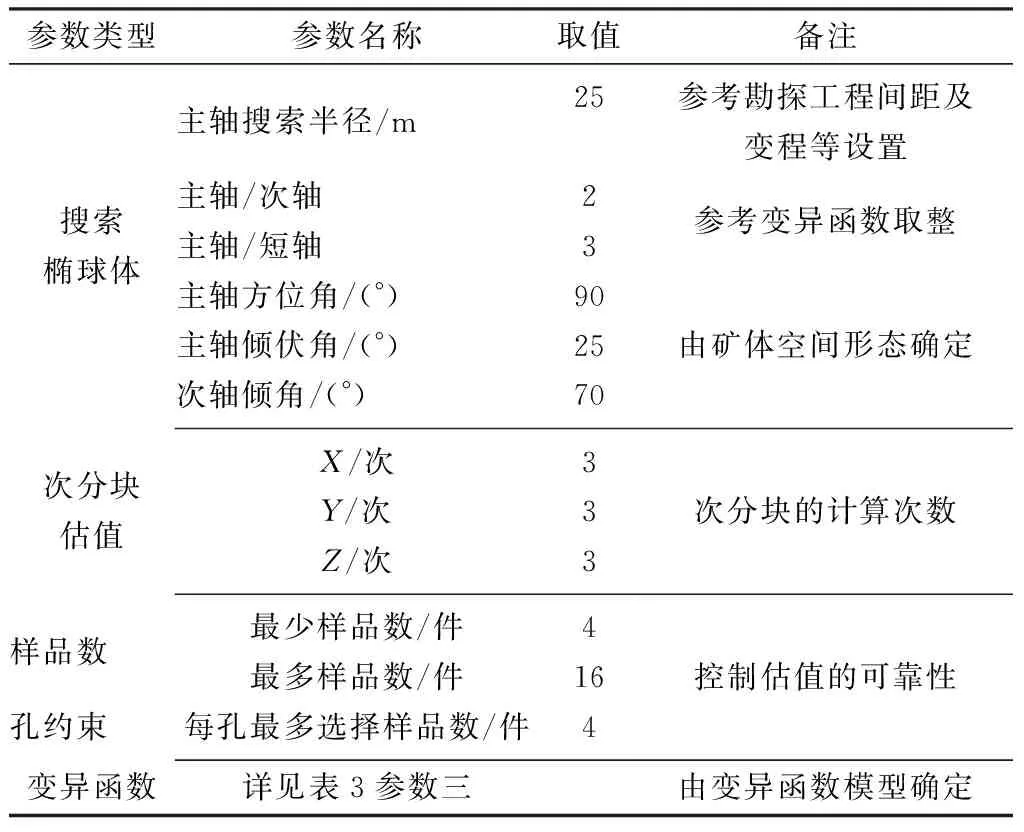
表4 普通克里格法估值参数Table 4 Estimation parameters of ordinary Kringing method

同时，将到样品点最近距离、到样品点平均距离、样品点数目、克里格方差、克里格效率、负权重数目、拉格郞日因子等信息写到块体中，以便对估值后的块体进行统计分类。

6.2 估值结果验证

采用全局验证的方法对估值结果进行检验。在平面图上按20 m的间距布设9条南北向勘探线，共划分9个区域(图8)。分别计算每一个区域内参与估值的组合样品平均值与块体模型估值的平均值，结果绘制成两条曲线图，其下方为对应的样品数(图9)。由图9可知，块体估值结果与实际样品点平均品位较为接近，估值曲线拟合了实际品位变化，整体而言，两条曲线吻合度较高，说明本次估值较为合理可靠。在5号勘探线、7号勘探线、8号勘探线，估值品位比样点平均品位低0.1 g/t，可以发现这三个区域样品点数相对较少，但同时估值的块体较多，估值距离增大，是造成估值结果偏差增加的原因。

6.3 资源量分类

地质统计法估算的资源量，可根据块体属性中的最近距离、平均距离、工程数、样品数等记录内容，或是搜索半径等进行资源量分类[18]。本文依据块体估值获取得到样品点的平均距离，按0～50 m及50 m以上，分别对相应块体属性设置为控制和推断类别。

矿化域模型不仅估算了一般工业品位以上的资源量，还估算了矿化域品位边界值至一般工业品位区间的矿石量、平均品位、金属量等信息，并可按品位变化进行统计(图10)，因此，在工业指标论证[9]、矿化特征分析[19]、成矿预测[8]等方面具有优势。

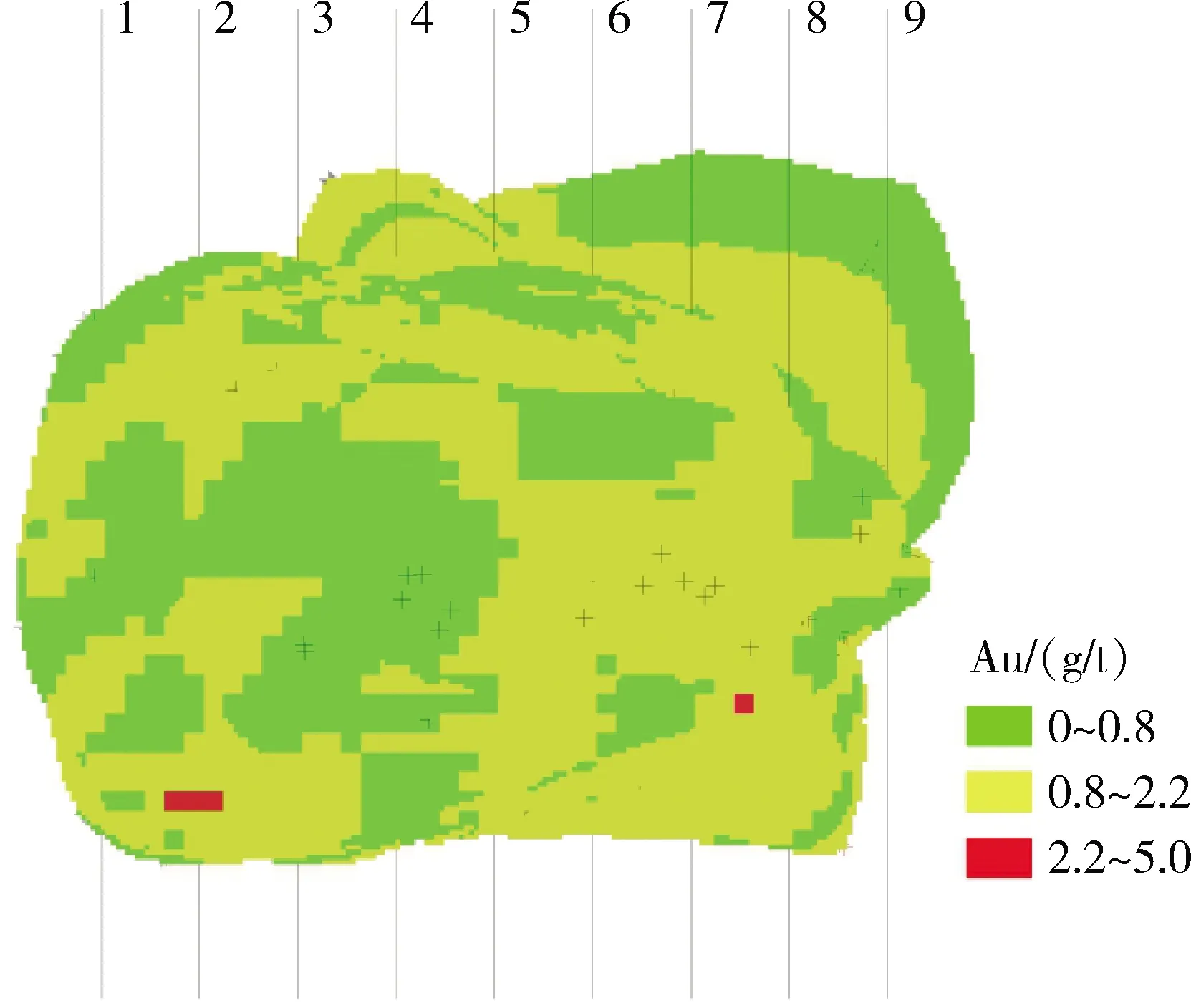
图8 全局验证示意图Fig.8 Schematic diagram of global verification

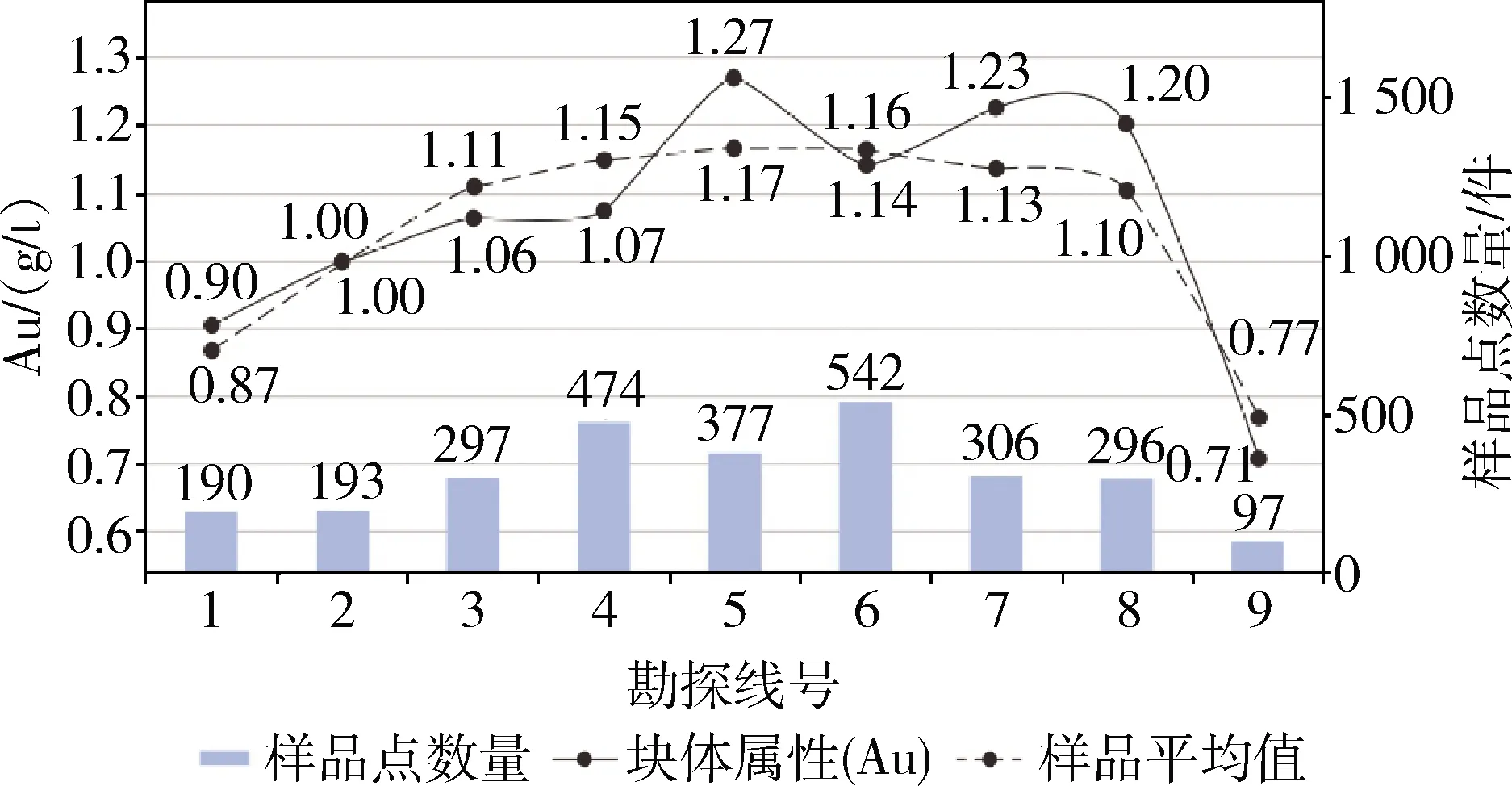
图9 全局验证曲线图Fig.9 Global verification diagram

图10 矿化域品位-资源量统计图Fig.10 Combination diagram of mineralized domain grade and resource changes

7 结 论

本文基于三维地质软件平台及矿化域估算理论，通过对澳大利亚某大型金矿样品的统计与分析，确立了矿化域品位边界值，建立了三维矿化域实体与块体模型；进一步对矿化域内样品进行地质统计分析，进行特异值处理及变异函数优化，最终以普通克里格法进行资源量估算。通过上述研究，主要得出以下结论。

1) 矿化域模型进行资源量估算，不仅估算了边界品位以上矿体，对低于边界品位的矿化部分也进行了估值，在品位指标论证时更为便捷高效。

2) 矿化域模型可以最大限度保留矿化的连续性，反映矿化的自然规律，展现矿化体的真实形态，有利于后期成矿预测。

3) 基于地质统计理论，对矿化域品位边界值、特异值、变异函数等参数进行优化，是保证估算质量的重要步骤。