统计方法在能力验证过程中的影响分析

◎ 许 辉，王金花，周 茜，逄昔莎

（1.必维信诺（山东）检测技术有限公司，山东 青岛 266101；2.青岛海关技术中心，山东 青岛 266109；3.青岛蔚蓝生物集团有限公司，山东 青岛 266102）

能力验证是实验室质量保证体系的重要组成部分，其本质是为了提升实验室的技术能力[1]。通过相关能力验证计划，实验室可客观评价其检测数据的准确性和可靠性。然而能力验证的结果在很大程度上受统计方法的影响，不同统计方法的选择通常会让结果有所差异，因此为了保证能力验证结果的准确性，需要注重统计方法的适用性。

1 数据统计方法

目前，国内外能力验证组织者通常采用Z比分数对结果进行评价，其中：

式中：x为实验室测试结果；X为指定值；σ为能力评定标准差。

能力验证用Z比分数对参加者的能力进行评定，当|Z|≤2时为结果满意，2＜|Z|＜3时为结果可疑，|Z|≥3时为结果不满意。对单次能力验证计划，通常采用经典统计方法或稳健统计方法。不同统计方法其指定值和能力评定标准差在选取上存在一定的差异。

2 经典统计方法

经典统计方法需要剔除离群值，其中离群值的剔除，可以使用格拉布斯（Grubbs）准则[2]，即式（2）计算：

式中：xn为实验室测试结果；为样本平均值，即指定值；s为标准偏差，即能力评定标准差。

在确定数据个数n以及显著性水平α后，查格拉布斯检验法临界值表，若Gn＞Gα,n，则xn为离群值。格拉布斯检验法临界值表如表1所示。本文采用食品分析实验室质量评估体系（Food Analysis Performance Assessment Scheme，FAPAS）组织的某次能力验证数据进行分析，α取95%置信区间。

表1 格拉布斯检验法临界值表

3 稳健统计方法

3.1 迭代法

迭代法将数据由小到大排列，对数列两端的数据按较小权重进行保留，而对接近中位值的数据以较大权重介入计算，能充分利用全部数据，是被推荐的稳健统计方法[3]。迭代法计算方法如下。

再由下式计算x*和s*的新的取值：

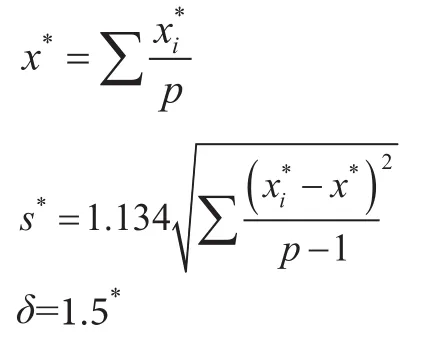
其中最后一次迭代的x*和δ即指定值和能力评定标准差，相关迭代计算过程和Z比分数如表2所示。

续表2

3.2 中位值和标准化四分位距法

将一组数据由小到大进行排列，其中位于中间位置的数据即中位值，位于上1/4处（QU）的数据为上四分位数（Q3），位于下1/4处（QL）的数据为下四分位数（Q1）。四分位距（IQR）为上下四分位数的差值，即IQR=Q3-Q1。标准化四分位距（NIQR）等于四分位距（IQR）乘以因子0.741 3，即NIQR=0.741 3×IQR。目前，四分位数位置的确定一般采用两种计算方法，见式（3）、式（4）：

两式中：n为数据个数，其中当QL、QU为整数时，Q1、Q3分别取对应位置的数值；当QL、QU不为整数时，则需按比例分摊位置两侧数值。

本例中，共有60个实验室结果，按照式（3）计算可得QL=15.25，QU=45.75，即说明Q1位于15、16结果中更接近15的位置，Q3位于45、46结果中更接近46的位置，故Q1=0.67×0.75+0.70×0.25=0.677 5，Q2=1.20×0.25+1.25×0.75=1.237 5；同理，式（4）计算可得Q1=0.692 5，Q2=1.2125。

目前，使用SPSS软件内部命令所得的IQR值，是通过式（3）的计算方式获得，而使用EXCEL软件内部命令所得的IQR值，则是通过式（4）的计算方式获得。两种计算方式所得的NIQR有一定的差异，如表3所示。

表3 两种方法计算所得的四分位结果表

3.3 Horwitz方程法

Horwitz方程法是一种国际公认的统计方法，为保证化学分析质量评定体系的一致性，国际标准化组织（International Organization for Standardization，ISO）、国际分析化学家协会（Association of Official Agricultural Chemists，AOAC）、国际纯粹与应用化学联合会（International Union of Pure and Applied Chemistry，IUPAC），曾在国际公约议定书中共同签署了相关规定[4-5]。Horwitz-方程法见式（5）：

式中：σR为能力评定标准差；c为稳健平均值，即指定值，其值可通过迭代法获得。本例中c为1.01，其单位为 μg·kg-1，故c＜ 1.2×10-7，σR值为 0.222 2。

3.4 不同方法所得Z比分数统计

不同方法获得的Z值如表4所示。

表4 不同方法所得Z比分数统计表

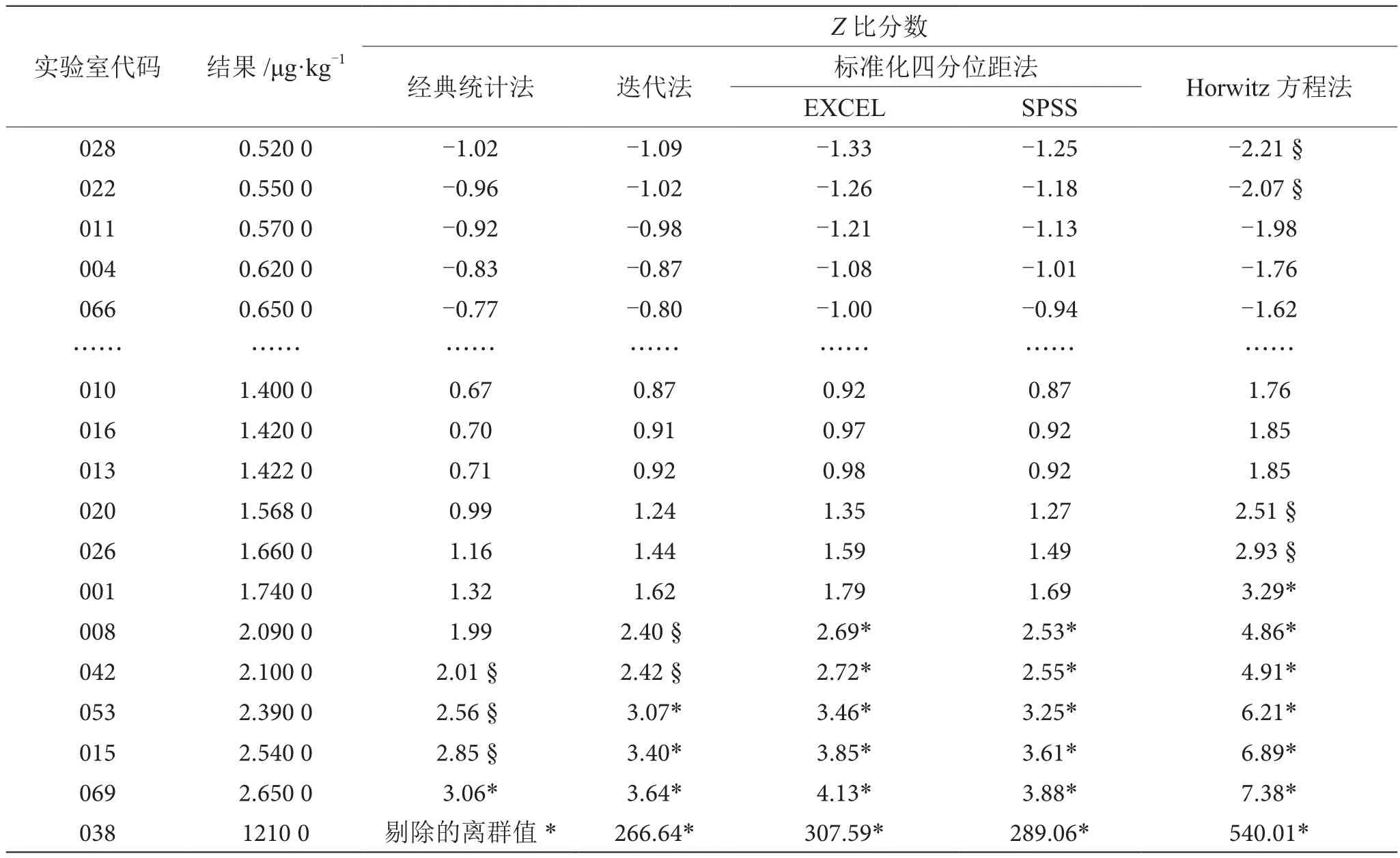
续表4

4 讨论

本文中选取的样本符合正态分布。通过表4可以发现，经典统计法较稳健统计法在“离群”结果的判定上明显较少，存在着统计学上取伪的风险，可能影响实验室检测能力的公正评价，这是因为经典统计方法中所有数据均参与了计算且权重相同。当一组数列中所有参数均作出贡献时，一旦存在极端值，则该组数据的平均值和标准偏差会受到极大的影响，进而统计结果的离散度会扩大，导致最终统计结果的不准确。

迭代法作为推荐的稳健统计分析方法，也具有经典统计法的特点。迭代法在计算过程中，通过减小“离群值”和“可疑值”的权重，降低了此类数据对结果的影响，同时用删掉离群值后的经典统计法结果作为判断依据，在指定值的选择上，准确性更高。中位值和标准化四分位距法因为IQR的计算方式不同，本身在Z比分数计算时存在差异，但总体而言对实验室结果的评定是一致的。

迭代法、中位值和标准化四分位距法作为目前国内最常用的能力验证统计方法，对能力验证数据的结果表述均具有较高的准确性和适用性。但是如表4所示，这两类方法与Horwitz方程法相比，在“可疑”及“离群”数据的判定上仍存在有较大差异。几种方法相较而言，Horwitz方程法的结果更符合实际过程中检测结果的表述。

Horwitz方程法较其他方法具有一定的优势，这是因为Horwitz方程法的指定值由迭代法得到，能保证其选择的准确性。另外，最主要的是Horwitz方程法将能力评定标准差与待测组分的浓度直接用函数式表示，克服了以前用绝对误差和相对误差评判的主观性和经验性，用来评判比对试验的结果更为客观、准确，因此可以保证统计结果的准确性更高、适用性更强。

本文中所选取的样本数量较大，因此各种统计方法都能得到良好的结果表述。但在实际过程中，往往会遇到样本数量较少的情况，此时其他方法在结果的表述上就存在着极大的局限性，但Horwitz方程法不受相对误差评判等的影响，因此对结果的表述依旧具有极高的准确性。

目前，国际上能力验证组织者，如食品分析能力评价体系（FAPAS）等机构普遍采用Horwitz方程法进行能力验证结果的统计，但在国内的能力验证过程中该方法鲜有涉及。建议有关部门将Horwitz方程法列入规定的能力验证统计方法之中。