跨越三种孔隙度地层的垂直裂隙对有机朗肯循环地热发电性能影响

高翔　李太禄　张维明　孟楠

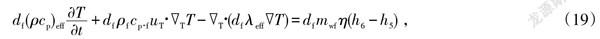
摘要 建立了一种垂直主裂缝跨越3层不同孔隙度的地热储层模型，对增强型地热系统的地热储层进行数值模拟，并将其与有机朗肯循环发电性能进行耦合和分析，计算和分析了注入温度、注入流量、裂隙宽度和裂隙粗糙度4个储层参数对生产井产能和干热岩发电性能影响，最终定量分析了4种特征对生产井温度和单位输出功的不同影响度。结果表明系统在前30年工作周期内，在第5年之前，改变注入温度对增强型地热系统的影响较小。在不考虑储层中换热流体渗漏的情况下，注入井流量越大，生产井温度越低;注入井温度越高，生产井温度越高。对于地面发电系统，注入温度对发电性能影响最显著，注入流量对地面发电系统影响较小，即地热储层结构对发电系统的输出功、   效率及   损失有决定性的影响。

关 键 词 增强型地热系统;垂直裂隙;有机朗肯循环系统;数值模拟;   分析

中图分类号 TK529     文献标志码 A

Analysis of the power generation performance of organic Rankine cycle with vertical fracture over three different porosity layers in reservoir

GAO Xiang LI Tailu ZHANG Weiming MENG Nan

Abstract This paper establishes a model of enhanced geothermal systems. The reservoirs contain a single primary vertical fracture cutting through three different porosity layers. On the basis of the numerical simulation in the reservoir of enhanced geothermal reservoirs， the coupled analysis between the organic Rankine cycle （ORC） and numerical results is obtained. In this analysis， the injection temperature， the injection mass flow， the width of primary fracture， and the roughness of the primary fracture are employed to investigate the production temperature and unit output work. The results show that the four parameters have different influence on injection temperature and unit output work. For the enhanced geothermal system in 30 years life cycle， the difference of the injection temperature has a little impact for the coefficient of power generation before the fifth year. Without considering the leakage effect in the reservoir， the higher the injection well flow， the lower the temperature of the producing well; the higher the injection well temperature， the higher the producing well temperature. For the power generation system， the injection temperature has the most significant impact on the power generation performance， while the injection flow rate has a small impact on the ground power generation system. The structure of geothermal reservoir has a decisive impact on the output work， exergy efficiency and exergy loss of the power generation system.

Key words enhanced geothermal system; a single primary vertical fracture; organ Rankine cycle （ORC）; numerical simulation; exergy analysis

引言

全球变暖将对人类生活产生巨大影响，在能源应用方面，用于发电的常规化石燃料燃烧排放大量的温室气体，将进一步加剧温室效应。为了减缓全球变暖，利用可再生能源发电是减少温室气体排放的有效措施。据统计，地热资源作为可再生能源，能够开采的地熱潜能在3 km以下的深度超过118 EJ/y，在10 km的深度超过1 109 EJ/y [1-2]。根据地下岩石特征，地热系统可分为热液系统和增强型地热系统。对于热液系统，地下储层的主要特征是高渗透性，并存在地下渗流。而增强型地热系统可以提取干热岩石中的热量，并通过有机朗肯循环转化为电能。其中干热岩为低渗透性脆性岩石，且在此深度下几乎没有地下水。与水热型系统相比，增强型地热系统可以在地热储层中通过水力压裂诱导产生人工裂缝而提取更多的热量进行发电。对于增强型地热系统，工程建设的主要过程如下：1）地热资源勘探;2）干热岩和天然裂缝的分布勘测;3）注入井钻探;4）通过水力压裂技术生成裂缝储层;5）构造由注入井，生产井和储量组成的地下循环系统;6）建设地上有机朗肯循环发电系统。其中储层模型的研究是增强地热系统的关键问题。

目前，增强地热系统的成本仍然很高。在过去的五年中，地热发电量平均每年增加500 MW，而这种增长大部分来自新兴经济体，因为它们拥有丰富且尚未开发的资源。根据IEA统计，到2030年，如果可持续发展情景中的发电量达到282 TW/h，则地热发电量每年需要增加10%的发电量。因此，应通过技术或政策来开发增强型地热系统以降低成本。当前成熟的模型有单孔隙度模型，双孔隙度模型和多孔隙度模型[3-4]，其中单一孔隙模型将储层描述为单一孔隙介质，该模型首先将储热区假设为单孔隙区，然后将单孔隙区划分为3个不同区域进行数值模拟。因此，在模拟和分析中忽略了裂缝的复杂结构，单一孔隙度模型不能准确地描述储层裂缝的复杂构造。双孔隙模型将裂缝储层视为多孔介质，由2个不同的多孔区域组成：裂隙网络视为理想的高孔隙度区域，而干热岩则视为低孔隙度区域。尽管双孔隙度模型的应用已经成功地描述了地热储层，但储层存在非均质性，该模型仍然存在问题。基于孔隙介质理论，多孔隙度模型基于原生裂缝、次生裂缝、断层和微裂缝，形成分层渗透结构或渗流通道，再对储层传热等过程进行数值模拟。目前，多孔隙度模型仍处于开发阶段。对于储层中的裂隙结构，基于传统弹性力学发展的PKN模型、KGD模型和P3D模型通常只能描述单个裂隙中的流动与裂隙热弹性问题[5-7]。对于多裂隙结构，当前离散随机网络模型能够对复杂的地下裂隙网络进行描述，但该种模型大多应用于地下流动过程，缺乏成熟的传热模型对传热-流动过程进行描述[8]。而上述所有的模型通常只对地热储层进行数值模拟，缺少对发电系统与地热储层之间的耦合关系进行研究，而地热储层作为热源对发电性能有关键作用，因此本文对增强型地热系统的裂缝储层模型进行数值模拟。对储层主要特征参数包括注入井温度、注入井流量、裂隙宽度和裂隙粗糙度进行研究。通过建立多孔介质模型对物理模型描述，本文分析了以上4种参数对生产井出口温度的影响，最终得出4种参数与出口温度的定量关系，并对模拟数值结果与增强型地热系统中的有机朗肯循环进行耦合，对有机朗肯循环的单位输出功进行了分析。

1 地热储层及有机朗肯循环（ORC）发电模型描述

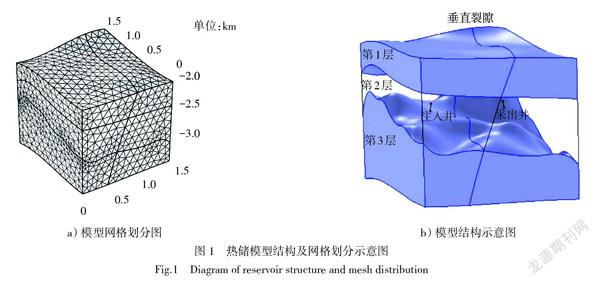
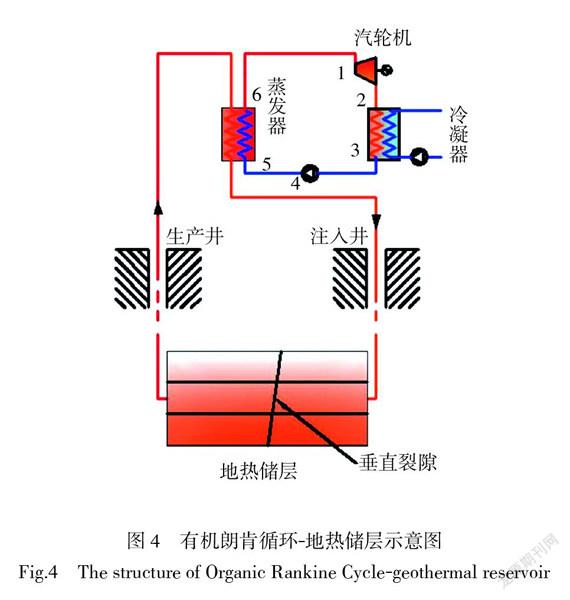
本文的所构建的物理模型如图1所示。图1所示的系统为双井式增强型地热系统。储层的模拟区域为1 500 m×1 500 m×1 500 m，模拟区域下表面距地表3 500 m，其中注入井与生产井位于同一水平面上，深度为2 500 m。为了减小数值模拟所需的计算资源，将注入井与生产井简化为长20 m的线热源与线热汇，忽略了实际过程中两井的井筒与周围储层的对流换热过程[9]。

对于储层，假设同一储层内为均匀介质，自上而下分为3种不同弹性力学性质的储层，其孔隙度分别为0.02、0.02、0.01，即人工裂隙大多分布在生产井与注入井所在的水平面上。在储层中存在一条主裂隙，其孔隙度为0.6。在储层的顶部平面与底部平面均假设没有流体流动，不考虑压降损失及裂隙渗漏效应。基于以上假设，本文采用了多孔介质传热模型对传热过程描述，并基于达西定律对流动过程进行了描述，通过COMSOL的耦合求解器对这一问题进行数值模拟。模型示意图及网格如图1a）和图1b）所示。

多孔介质中流体流动的连续性方程为[4，10-12]

式中：[ρf]为流体密度，kg/m3;φ为储层的孔隙度;t是时间，s;u是达西渗流速度，m/s;∇是矢量微分算子;[Qf]为流体在裂隙与干热岩的流动过程中的质量源项，kg/（m3∙s）。

由于流动过程服从达西定理[3，13-18]，u的表达式为

式中：k是储层的渗透率，m2，其中[k=d2f/（12ff）]，[ff]为裂隙粗糙度;[uf]是流体的动力黏度，Pa∙s;p为压力，Pa;[ρfg∇z]代表重力影响下的压力梯度，z代表垂直方向的分量。

多孔介质内能量方程为

式中：T为多孔介质温度，K;[cp，f]为流体的比热容，J/（kg∙K）;[ρcpeff]是有效容积;[λeff]是有效导热系数;[Qf，E]为裂隙与干热岩之间的传热量。

式（3）中[ρcpeff]和[λeff]可表示为

式中：[ρs]为储层中干热岩密度，kg/m3;[cp?f]为干热岩比热容，J/（kg[∙]K）;[λs]为干热岩导热系数，W/（m·K）。

同样地，裂隙的能量方程为

式中，[df]为裂隙宽度，m。

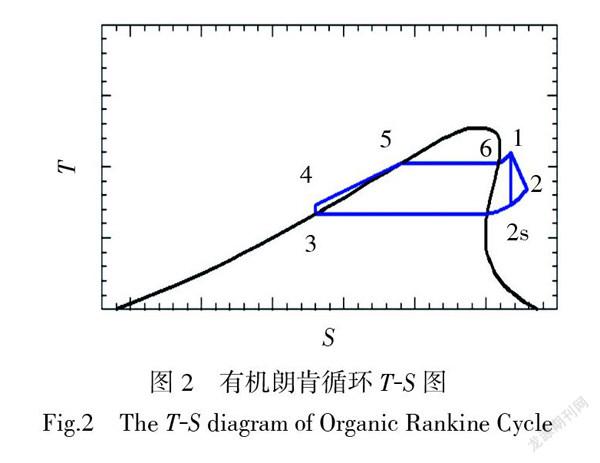
对于地面发电系统，本文建立了增强型地热系统中有机朗肯循环发电系统的模型，所计算的初始参数分别为：环境压力为101.3 kPa，汽轮机效率为0.75，冷却水进口温度为308.15 K，出口温度为318.15 K，冷凝器侧水泵扬程为20 m，水泵效率为0.9，有机工质采用R245fa，本系统的有机朗肯循环发电过程T-s图如图2所示。其中相关参数的计算模型如下所示：

式中：[t0]为环境温度;[h1]、[h2]分别为汽轮机进出口焓值;[h4]、[h5]分别为工质泵进出口焓值;[s1]、[s2]分别为汽轮机进出口熵值;[s4]、[s5]分别为工质泵进出口熵值;[hin]、[hout]分别为地热流体生产井、注入井焓值;[sin]、[sout]分别为地热流体生产井、注入井熵值;[Wt]为汽轮机输出功;[Wp]为工质泵耗功;[Whp]、[Wep]分别为蒸发器与冷凝器侧冷却水耗功;[ηhp]、[ηcp]分别为蒸发器与冷凝器的换热效率;[H1]、[H1]分别对应两个泵的扬程;[se]、[st]、[sc]、[sp]分别为图2对应1-5、1-2、2-4、4-5这4个过程的熵产;[s]为总不可逆损失与总熵产;[mwf]、[mcw]、[mgw]分别为工质质量流量、冷却水质量流量、地热流体质量流量;[Efc]、[Et]和[Ec]分别为1-4、4-5、5-6这4过程的热量    ;[Eground]为地热流体    损失;[ηex]为    效率。

因此，在满足达西渗流条件下，裂隙宽度与输出功之间关系可由式（19）表示

式中：η为效率系数;[df]为裂隙宽度。若发电系统为ORC系统，则η为发电系统热源侧换热器换热效率。因此， 由等式右侧[h6]和[h5]参数能够根据热力循环推导得出[h1]与[h2]，由式（19）建立了发电功率与地热儲层之间的耦合关系。

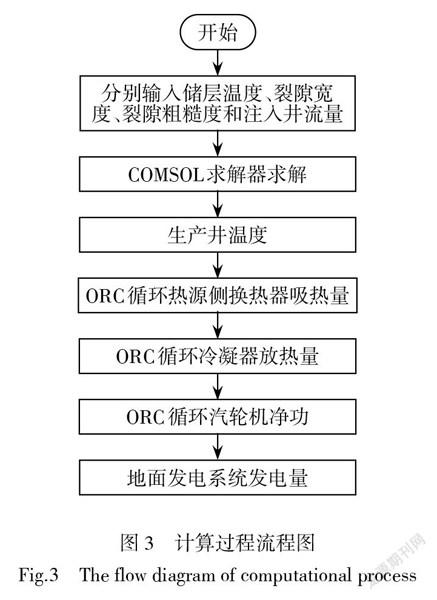
对上述公式在MATLAB和COMSOL实现，水和R245fa的热力学参数来自REFPORP软件，计算流程如图3所示，有机朗肯循环-地热储层结构如图4所示。

2 初始条件与边界条件

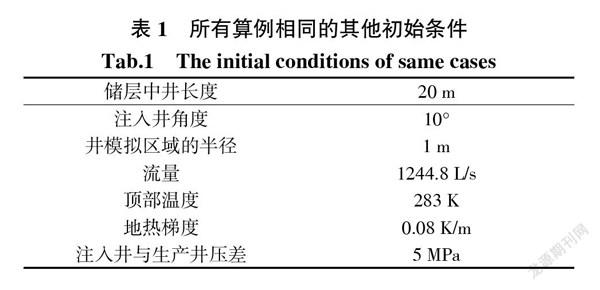
本文通过从模拟区域顶部边界面线性增加温度与压力来初始化储层，并忽略了换热流体在地热储层中的损失。相关的模拟参数来自于美国沙漠峰深层地热井[19-20]，地热梯度和注入井与生产井压力差分别为0.08 K/m和5 MPa。对于温度边界条件，模拟区域顶部平面与底部平面设置为绝热边界条件，且温度与初始储层温度相同[21-23]。对于流动边界条件，假设模拟区域外没有流体流动，因此在所有模拟区域边界面上设置无流体流动边界条件。对于初始条件，根据文献[20]中的实验数据，算例1模拟了在1.2 m3/s注入井流量时，注入井进口温度为313.15 K、333.15 K、353.15 K和373.15 K时生产井的出水温度;算例2模拟了注入井333.15 K时，注入井流量1.0 m3/s 、1.2 m3/s、1.4 m3/s和1.6 m3/s时生产井的出水温度;算例3模拟了333.15 K注入井温度，1.2 m3/s注入流量下时，主裂隙宽度分别为0.05 mm、0.1 mm、0.5 mm、1.5 mm和2 mm时生产井温度;算例4模拟了333.15 K注入井温度，注入井流量为1.2 m3/s时，裂隙内粗糙度分别为0.8、1.6和2.4时的生产井温度。

本文所进行的数值模拟的其他初始条件详细信息如表1所示。

3 地热储层模拟结果分析

3.1 注入井温度对生产井温度的影响

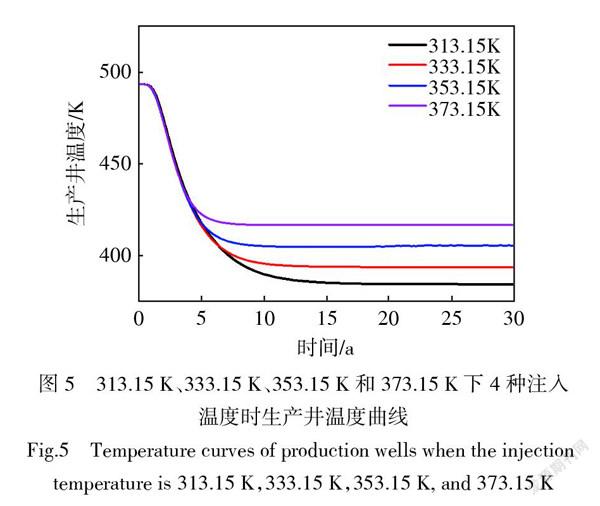
本文选取了313.15 K、333.15 K、353.15 K和373.15 K下4种注入温度时对储层进行模拟。模拟了30年内储层温度场的变化情况。如图5所示，在增强型地热系统工作的前5年内，4种注入温度对生产井的温度影响较小，所得的4种生产井温度接近，因此在工作的前5年内，改变注入温度对增强型地热系统的影响较小，可采用相对较低的注入温度来保持系统的发电性能。在第5年时，此算例下生产井温度为425 K左右，在第15年时，4种条件下的生产井温度产生了较大变化，当注入井温度为373.15 K时，其注入井温度比313.15 K的生产井温度高31 K，但此时注入井温度373.15 K比313.15 K高60 K，因此，以增强型地热系统的生命周期为例，当系统运行时间超过15年时，此时提高注入井温度并不能显著提高发电效率。第5年时，所有生产井温度均开始趋于平稳，主要原因为在初始5年运行时间以内，注入井与地热储层之间温差较高，换热量较大，得到的生产井温度较高;而伴随取热过程进行，储层温度逐渐降低，注入井温度保持恒定，二者温差减小，导致换热量减少，生产井温度逐渐降低。

另外，当运行时间超过15年后，各生产井温度趋于稳定，在算例的初始条件及边界条件下，每20 K注入井温差，将会在15年以后导致10 K左右的生产井温差。而在15年以前的运行阶段，不同情况下的生产温度之间的温差是非线性关系，存在注入温度越高，所获取的生产井温度越高的规律，这也与储层流动与传热的连续性方程和能量方程的非线性耦合关系相对应。

3.2 注入井流量对生产井温度的影响

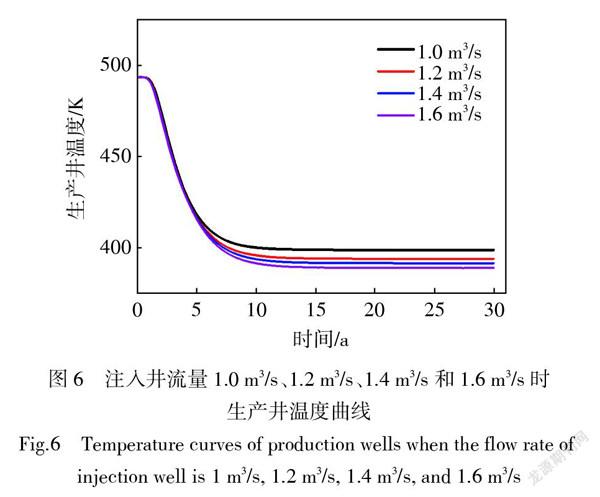
此算例选取了注入井流量1.0 m3/s 、1.2 m3/s、1.4 m3/s和1.6 m3/s 4种情况下，模拟了30年运行周期中生产井温度的变化情况，如图6所示。

不同注入井流量同样在前5年时的各自生产井温度近似相等，当运行时间达到10年才出现明显差别，且各自的差异近似线性。由于本文基于流体在储层中无损耗的理想性假设下，在控制方程中，流量与总换热量是线性关系。但在实际地热储层中，由于流体存在渗漏现象，注入井流量与生产井流量通常不相等。另外，渗漏过程与储热地层中的微裂隙有较大相关性，因此实际地热储层中的注入井流量与生产井温度之间的相关性，应通过实际储热地层结构数据进行分析。同样对15年后不同注入井流量下的生产井温度进行比较，发现1.6 m3/s注入井流量与1 m3/s注入井流量相比，其生产井温度降低了10 K左右，因此，增加注入井流量将降低地热储层的平均温度，生产井温度逐渐降低。虽然增加注入井流量将提高产热量，但从工程角度分析，增大流量需要增加注入井与生产井之间的压差，在此算例中，两井压差已设置为5 MPa，而在文献[21]中提到在当前技术条件下，达到此种压差耗费巨大，因此，增加流量所带来的发电收益较小。

3.3 不同裂隙宽度对生产井温度的影响

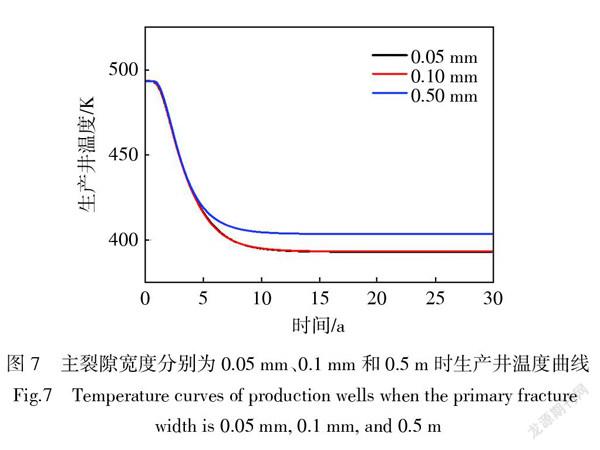
本文选取的主裂隙宽度分别为0.05 mm、0.1 mm和0.5 m。并分别对生产井温度的影响进行了模拟，模拟结果如图7所示。

由于本文中的主裂隙为一条垂直裂隙，并且跨越了3种地层，因此裂隙宽度越大，其换热量越大，由图7可得从第5年开始，0.5 mm裂隙宽度的生产井温度一直高于裂隙宽度较小的0.1 mm裂隙和0.005 mm裂隙，这主要因为本文所研究的主裂隙类型为垂直裂隙，此裂隙连通了3个地层。因此当运行时间增大时，且裂隙宽度较低时，经垂直裂隙传递的来自各个地层的热量远远小于裂隙宽度较大时所传递的热量，小裂隙宽度只能使大部分传热过程集中在两井所在的水平面处，而大裂隙宽度却能够连通不同地层，传递其他地层的热量，显著提高了生产井温度。

3.4 裂隙粗糙度对生产井温度的影响

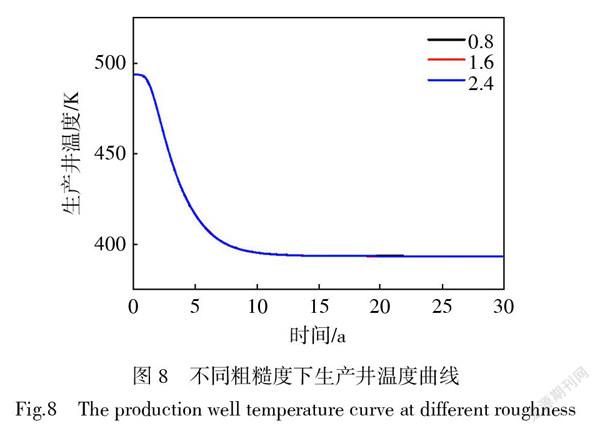
本文模拟了303.15 K注入井温度、1.2 m3/s注入井流量时，裂隙内粗糙度分别为0.8、1.6和2.4时生产井温度，模拟结果如图8所示。

如图8所示，不同裂隙粗糙度对生产井温度影响较小，而此算例下选取的裂隙宽度为0.05 mm，当裂隙宽度越小时，裂隙粗糙度对流体流动影响越大。但图中所示的差距卻很小，因此在实际工程中，裂隙粗糙度对生产井温度的影响可以忽略。另外，流体在裂隙中的流动过程复杂，并非层流，属于雷诺数较大的紊流，在流动过程中存在数量较多的涡流，干扰了流动边界层，削弱了裂隙粗糙度对流体流动与对流换热过程的影响。综上所述，对于地热储层，增大粗糙度对发电增产效果不显著，而裂隙宽度是主要影响生产井温度的因素。在水力压裂过程中，构建合理的裂隙结构能够有效提高生产井温度，从而提高发电功率。

4 增强型地热系统地上发电系统性能分析

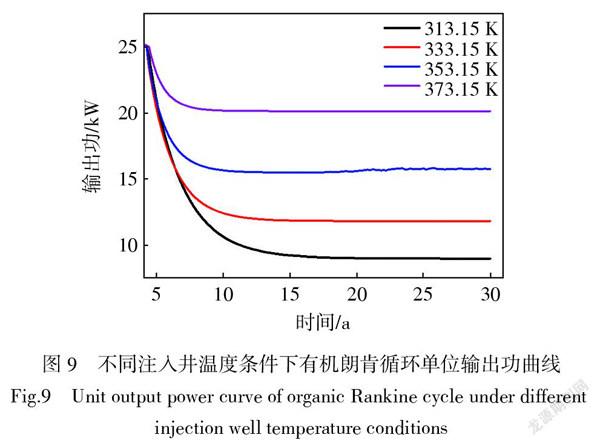
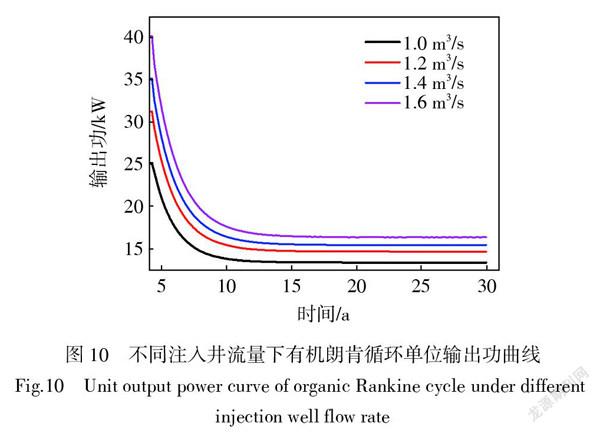
地热储层结构在运行过程中无法再次通过水力压裂技术重新生成裂隙，因此本文只对实际过程中易于控制且对发电效率影响较大的注入温度和注入流量进行分析，结果如图9和图10所示。

由图9可得，汽轮机单位输出功的变化趋势与生产井趋势相同。由于有机朗肯循环模型设定了汽轮机入口处压强上限，因此在图9中，从第4年开始绘制输出功曲线。以第10年最小的单位输出功为例，图9的单位输出功由19 kW左右衰减到10 kW，衰减幅度较大。为了保持较高的单位输出功，自第10年开始应提高注入井温度保持输出功。再通过图9与图10的对比，当运行10年以后，输出功趋于稳定时，注入井流量1 m3/s的输出功比1.6 m3/s仅高1 400 kW，因此改变注入井流量进行增产与改变温度相比效果较差。由于实际过程中地热储层存在渗漏现象，因此提高注入井温度比提高注入井流量更易实现。另一方面，提高注入井流量相当于提高了注入井与生产井之间的压差，而当前模拟条件下所设置的5 MPa压差已较大，因此，从成本与安全角度考虑，在此压差基础上继续提高注入井流量的存在技术限制。而本文又忽略了地热流体渗漏的情况，同时在其他文献研究中发现渗漏率跟储层结构相关[22]，因此，对运行10年以后的增强型地热系统进行增产，首选方式为提高注入温度。

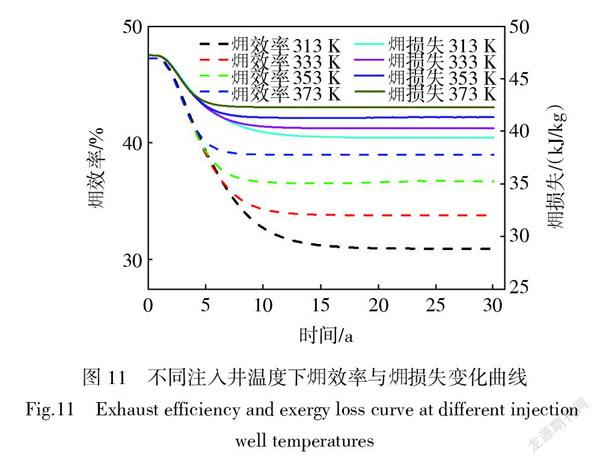
影响有机朗肯循环发电系统的一个重要指数为    效率，因此下文将结合有机朗肯循环发电系统与地热储层进行    分析。

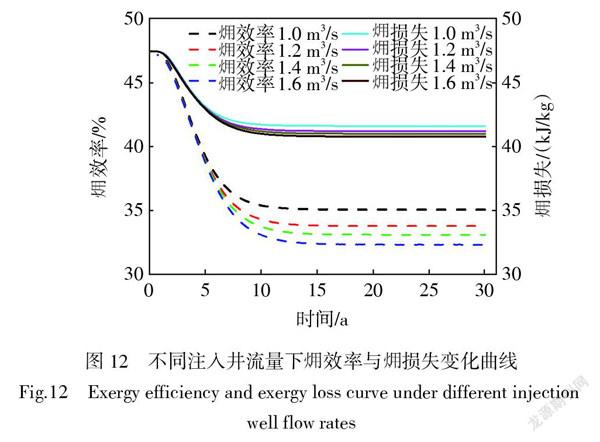
图11为注入井温度分别为313.15 K、333.15 K、353.15 K和373.15 K时，地面有机朗肯循环发电系统的    效率及    损失变化曲线。由图11可知，当注入温度从313.15 K增长到373.15K时，其    效率增加了10%，而    损失只升高了3 kJ/kg左右。因此，改变注入温度对系统    效率的影响较大，提高注入温度能显著增加地热储层的可用能。由图12可知，改变注入井流量对    效率及    损失影响较小，流量越小，    效率及    损失越高，因此，较小流量能够提高系统    效率，但同时也减小了换热流体携带的热量。在影响干热岩与水之间传热量的3种因素（换热时间、达西渗流速度、换热流体流量）之中，通过对图9和图10进行比较，发现存在流体流量越小，输出功、    效率和    损失均增大的规律，因此，在干热岩与水换热过程中，较小流量虽然直接降低了一部分换热量，但在小流量、低达西渗流速度的条件下，越小的流量使干热岩与水换热更加充分，即相对于增大流量，干热岩与水之间的换热过程对系统的输出功、    效率及    损失的影响更显著。

5 结论

本文对增强型地热系统的裂缝储层模型进行数值模拟。对注入井温度，注入井流量，裂隙宽度和裂隙粗糙度4种参数对生产井温度的影响进行分析。通过建立多孔介质模型对物理模型描述，得出4种参数与出口温度的定量关系。并通过数值模拟对增强型地热系统中的有机朗肯循环进行耦合并对单位输出功进行分析。主要结论如下：

1）在增强型地热系统前30年工作周期内，在第5年之前，改变注入温度对增强型地热系统的影响较小，可采用相对较低的注入温度来保持系统的发电性能。

2）在不考虑储层中换热流体渗漏的情况下，注入井流量越大，运行时间第15年以后储层温度趋于稳定时，生产井温度越低;当注入井温度越高，运行时间第15年以后储层温度趋于稳定时，生产井温度越高。

3）对于垂直主裂隙，其粗糙度对生产井温度影响较小，其宽度在4种影响因素中对生产井影响最显著。

4）在影响有机朗肯循环系统输出功的因素中，干热岩与换热流体的传热过程对输出功、    效率及     损失影响最显著，换热流体流量对输出功、    效率及    损失影响最小，即地热储层结构对发电系统的输出功、    效率及    损失有决定性的影响。

参考文献：

[1]    BATAILLÉ A，GENTHON P，RABINOWICZ M，et al. Modeling the coupling between free and forced convection in a vertical permeable slot：implications for the heat production of an Enhanced Geothermal System[J]. Geothermics，2006，35（5/6）：654-682.

[2]    JIANG F M，CHEN J L，HUANG W B，et al. A three-dimensional transient model for EGS subsurface thermo-hydraulic process[J]. Energy，2014，72：300-310.

[3]    CORREIA M G，VON HOHENDORFF FILHO J C，SCHIOZER D J. Development of a special connection fracture model for reservoir simulation of fractured reservoirs[J]. Journal of Petroleum Science and Engineering，2019，183：106390.

[4]    STEPHENS J C，JIUSTO S. Assessing innovation in emerging energy technologies：Socio-technical dynamics of carbon capture and storage （CCS） and enhanced geothermal systems （EGS） in the USA[J]. Energy Policy，2010，38（4）：2020-2031.

[5]    PERKINS T K，KERN L R. Widths of hydraulic fractures[J]. Journal of Petroleum Technology，1961，13（9）：937-949.

[6]    GEERTSMA J，DE KLERK F. A rapid method of predicting width and extent of hydraulically induced fractures[J]. Journal of Petroleum Technology，1969，21（12）：1571-1581.

[7]    ADACHI J I，DETOURNAY E，PEIRCE A P. Analysis of the classical pseudo-3D model for hydraulic fracture with equilibrium height growth across stress barriers[J]. International Journal of Rock Mechanics and Mining Sciences，2010，47（4）：625-639.

[8]    HOFMANN H，BABADAGLI T，ZIMMERMANN G. Hot water generation for oil sands processing from enhanced geothermal systems：process simulation for different hydraulic fracturing scenarios[J]. Applied Energy，2014，113：524-547.

[9]    LI S B，FENG X T，ZHANG D X，et al. Coupled thermo-hydro-mechanical analysis of stimulation and production for fractured geothermal reservoirs[J]. Applied Energy，2019，247：40-59.

[10]  JIANG F M，LUO L，CHEN J L. A novel three-dimensional transient model for subsurface heat exchange in enhanced geothermal systems[J]. International Communications in Heat and Mass Transfer，2013，41：57-62.

[11]  TESTER JW ，LIVESAY B，ANDERSON B J，et al. The future of geothermal energy：impact of Enhanced Geothermal Systems （EGS） on the United States in the 21st century[Z]. An assessment by an MIT-led interdisciplinary panel，2006.

[12]  EVANS K. Enhanced/engineered geothermal system：An introduction with overviews of deep systems built and circulated to date//[C]China geothermal development forum. Beijing，2010，24：395-418.

[13]  BARENBLATT G I，ZHELTOV I P，KOCHINA I N. Basic concepts in the theory of seepage of homogeneous liquids in fissured rocks[strata[J]. Journal of Applied Mathematics and Mechanics，1960，24（5）：1286-1303.

[14]  WARREN J E，ROOT P J. The behavior of naturally fractured reservoirs[J]. Society of Petroleum Engineers Journal，1963，3（3）：245-255.

[15]  GILMAN J R. An efficient finite-difference method for simulating phase segregation in the matrix blocks in double-porosity reservoirs[J]. SPE Reservoir Engineering，1986，1（4）：403-413.

[16]  GILMAN J R，KAZEMI H. Improved calculations for viscous and gravity displacement in matrix blocks in dual-porosity simulators （includes associated papers 17851，17921，18017，18018，18939，19038，19361 and 20174）[J]. Journal of Petroleum Technology，1988，40（1）：60-70.

[17]  PRUESS K，NARASIMHAN T N. A practical method for modeling fluid and heat flow in fractured porous media[J]. Society of Petroleum Engineers Journal，1985，25（1）：14-26.

[18]  FUNG L S K. Simulation of block-to-block processes in naturally fractured reservoirs[J]. SPE Reservoir Engineering，1991，6（4）：477-484.

[19]  ZENG Y C，SU Z，WU N Y. Numerical simulation of heat production potential from hot dry rock by water circulating through two horizontal wells at Desert Peak geothermal field[J]. Energy，2013，56：92-107.

[20]  ASAI P，PANJA P，MCLENNAN J，et al. Efficient workflow for simulation of multifractured enhanced geothermal systems （EGS）[J]. Renewable Energy，2019，131：763-777.

[21]  翟海珍，金光榮，古锐开，等. 换热单元体展布特征对水平井多级压裂的EGS采热的影响[J]. 太阳能学报，2020，41（7）：64-72.

[22]  单丹丹，闫铁，李玮，等. 单裂隙热储热流耦合数值模拟分析[J]. 当代化工，2020，49（4）：716-719，723.

[23]  李盼. 干热岩CO2-EGS中热-流-固-化耦合效应研究[D]. 徐州：中国矿业大学，2020.

收稿日期：2021-01-27

基金项目：国家重点研发计划（2018YFB1501805）;广东省自然科学基金（2018A0303130181）

第一作者：高翔（1995—），男，硕士研究生。通信作者：李太禄（1982—），男，副教授，2018020@hebut.edu.cn。