一种针对无键相铁道车辆的旋转部件阶次跟踪方法*

曾陆洋，延九磊，刘 峰，辛恩承，史 稷

（1 北京纵横机电科技有限公司，北京 100094；2 中国铁道科学研究院集团有限公司 机车车辆研究所，北京 100081；3 中国铁道科学研究院集团有限公司 高速铁路与城轨交通系统技术国家工程研究中心，北京 100081）

针对铁道车辆运行速度不断变化以及振动故障特征非平稳的特点，上世纪90年代的等角度变频采样与阶次跟踪技术，能够避免旋转部件在变转速下常规快速傅里叶分析中出现的“频率模糊”现象［1］，如图1所示，这已经成为铁道车辆旋转部件故障诊断与分析中必不可少的重要手段之一，目前在故障预测与车辆检修方面有着广泛应用。

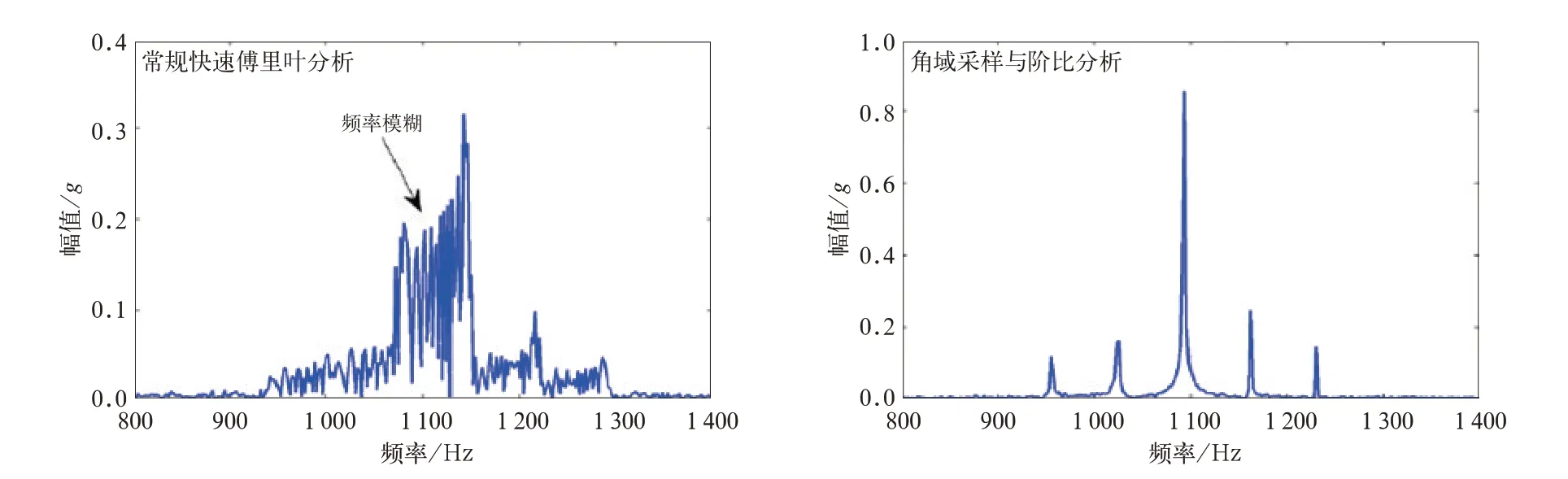
图1 等角度变频采样与阶次跟踪避免“频率模糊”现象

等角度变频采样通常需要轮对或轴承的转速键相信号作为触发采样的条件，实际中大部分铁道车辆都安装了转速键相装置，主要应用于防滑器或测量牵引电机状态等方面，而能够被振动检测设备直接获取转速键相信号的车型较少，大量的25型客车、CRH系列和谐号动车组、CR400系列复兴号动车组配置的振动检测设备无法获取转速键相信号。

近年来众多学者针对如何在无键相的条件下实施阶次跟踪展开了大量的研究工作。根据传统有键相硬件触发的阶次跟踪原理可知，如何获得回转轴的转速是阶次跟踪技术的最核心问题之一［2］。目前的解决方案通常采用时频法或HHT等技术获取瞬时转频（或其倍频），进而通过重采样完成无键相阶次跟踪。但时频法在转速频率成分较为单一的条件下准确率较高，而针对复杂成分振动信号的转速估计则存在较大波动［3］；HHT法则由于边界效应尚未完全解决，使得在工程化应用中存在局限性。

因而文中在时频法基础上，利用列车网中周期发送的全列运行速度约束峰值提取区间，以提高转速估计的准确性。进而利用等角度间隔重采样、角度域同步平均降噪等处理实现对无键相铁道车辆的旋转部件阶次跟踪。

1 无键相阶次跟踪方法

1.1 基于区间约束峰值提取的转速估计

旋转部件的振动信号通常包含转频成分以及转频的各次谐波，其关系为式（1）：

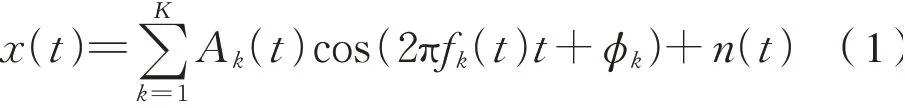
式中：A k（t）为k次谐波的瞬时幅值；fk（t）为k次谐波的瞬时频率；ϕk为k次谐波的相位；n（t）为系统噪声。

由于旋转部件各次谐波的瞬时频率与转频f1（t）之间满足的线性比例关系为式（2）：

这样，瞬时转速的求取问题可转化为第k次谐波的瞬时频率估计问题［2］。

在实际工程运用中根据研究对象的运行物理特性不同，通常选取不同阶次的谐波为估计对象。如轮轴的转速估计因铁道车辆蛇行运动特性通常选取横向振动的转速1倍频，齿轮箱的转速估计因齿轮啮合特性通常选取啮合频率（可看作转频的齿数次谐波）。

多分量振动信号的瞬时频率可通过时频法来获取，由于振动信号的时频分布在转频（或其谐波）临近的局部区间内存在能量脊线，如图2所示，且利用25型客车、CRH系列和谐号动车组、CR400系列复兴号动车组等车型列车网中周期发送的全列运行速度经式（3）简单变换后可得到转速的近似区间：

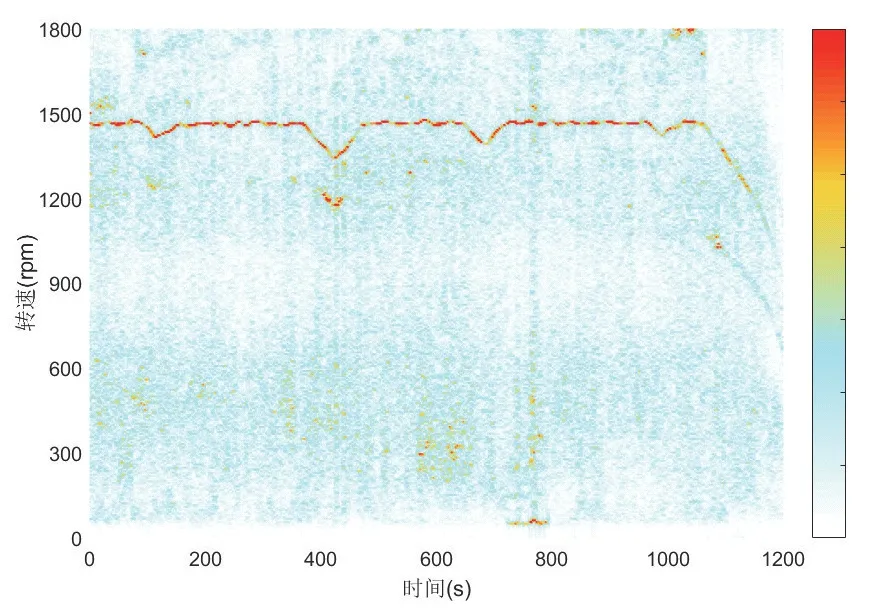
图2 轮轴横向转频能量脊线

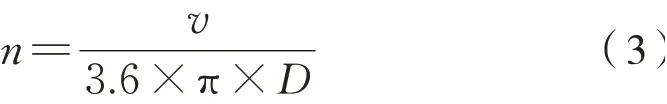
式中：n为转速，r/min；v为列车网中发送的全列运行速度，km/h；D为轮径值区间，m，上限为新轮轮径值，下限为修程规定的报废轮径值。

故基于全列运行速度对振动信号的时频分布进行有约束的峰值提取，此时峰值对应频率即为转速的瞬时频率。

计算流程如下：

（1）采集被测对象振动信号x（t）。

（2）采集x（t）对应时间下列车网发送的全列运行速度v（i）（i=1，2，...，m）。

（3）选定窗长，基于FIFO原则滑动截取振动信号，得到xi（to）。

（4）对每段数据做FFT得到xi（f）。

（5）对v（i）做式3中线性变换得到nmin（i）与nmax（i）。

（6）在［nmin（i），nmax（i）］内对xi（to）进行峰值搜索得到转速曲线n（i）。

需要说明的是，铁道车辆旋转部件实际运行中，在个别转速下振动信号与其他频率成分交叉影响估计精度，可通过同时估计转频的2、3倍频作为修正，或对n（i）做卡尔曼滤波以提高准确性。

1.2 等角度间隔重采样

考虑到旋转机械振动信号是以转角位置为自变量的周期平稳信号，人们提出了等角度采样方法将非平稳的时域采样信号变成角域里周期平稳的信号［4］。利用估计的转速信号获得等角度采样的键相时刻，然后在键相时刻进行幅值插值即可得到等角度间隔重采样信号。

转速信号可通过对3个连续的转速估计值进行局部二次多项式拟合，得到式（4）：

设采样时间为T0-T n，等角度间隔重采样点数为N，每转过Δθ角度重采样一次，则有式（5）：

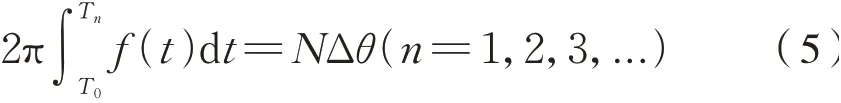
从而得到等角度采样的键相时标T i（i=1，2，3，…，N）为式（6）：

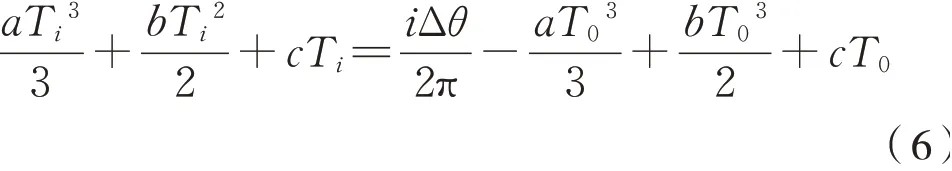
式中：T i是第i个点的重采样时刻；Δθ是角度增量。

得到Δθ的所有重采样时刻T i（i=1，2，3，…，N）后，对等时间间隔采集的原始数据进行幅值插值即可得到等角度重采样的振动数据，如图3所示。

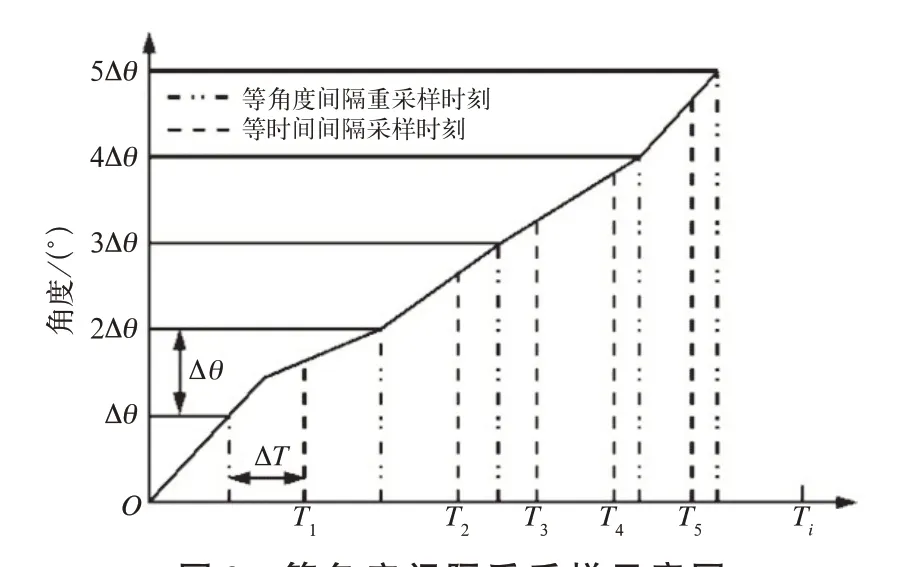
图3 等角度间隔重采样示意图

1.3 等角度同步平均

时域同步平均方法原本是从含噪声振动信号中提取出周期成分的有效方法之一，该主要通过对时域信号的周期截断和均化处理，实现对周期成分的保留和增强。

基于时域同步平均的数学思想，通过角度域同步平均的概念对重采样后的振动信号进行降噪处理。角度域同步平均主体思想是从含随机噪声信号中提取与转频（或其谐波）相关的周期性信号的过程［5］，不仅可以降低系统噪声干扰，同时还能抑制与转频非相关的振动成分（使其谱峰发生频散现象）。

假定采集的信号x（θ）由周期信号p（θ）和噪声信号n（θ）组成，为式（7）：

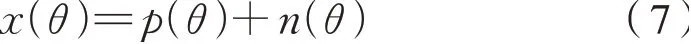
以信号p（θ）的角度周期去截取信号x（θ）可得到k段信号，对得到的k段信号进行叠加，由于p（θ）在其角度周期上为稳态，而k段随机噪声信号n（θ）之间不相关，根据信号叠加原理，故有式（8）：

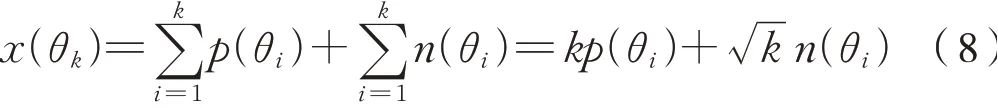
再对叠加了k段的信号x（θk）取均值，可得到信号y（θk），为式（9）：

此时输出信号中噪声是原输入信号x（θ）中的，因而信噪比提高了倍。

1.4 阶比谱分析

类似于对时域信号进行的快速傅里叶分析，也可通过对角域信号进行FFT而获得阶比谱。阶比谱能够揭示出各阶次（谐波）的幅值关系，通常阶比谱分析过程中将转速、幅值、频率或阶次相结合，组合构成转速谱阵进行研究。

关于轮对、轴承等旋转部件的典型故障在阶比谱中表现出的特征及判别方法，此前已有大量学者提出了较为成熟的方案，在此不再赘述。

2 旋转部件故障台架试验及分析结果

利用旋转部件故障试验台实测含有键相信号的轴承外环剥离振动数据设计验证试验，（特征频率为5.278倍转速）通过对比分析传统硬件模式触发等间隔角域采样的阶比谱和利用上述方法处理的无键相等间隔角域重采样以及等角度同步平均后的阶比谱，以验证上述方法的准确性。

本试验平台由电机、测试轴承（以轴箱轴承作为研究对象）、磁粉制动器（负载）、转速传感器和若干加速度传感器等组成，采样频率为12 kHz，试验平台如图4所示。

图4 旋转部件故障试验台

测试数据通过传统硬件触发等间隔角域采样方案获取，为保证数据的真实性，采集主机、加速度传感器、转速传感器型号均与实车配置保持一致。利用转速传感器获取转速的键相信号，轴承每转过一个相同的角度将产生一个高低相间的矩形脉冲信号，将该信号输入到采集主机AD模块对矩形脉冲进行倍频处理，并在上升沿时刻触发对加速度信号的采样，实现等角度间隔采样。其流程如图5所示。

试验台在运行过程中能够每秒以数字信号的形式同步输出转速信息，试验中将该转速经式（3）反变换后（D取0.9 m）以模拟振动监测主机从列车网获取到的速度。

试验结果如图6所示。试验中台架电机以图6（a）曲线进行变转速运动。图6（b）为常规FFT分析结果，可见在变转速下频谱出现了明显的“频率模糊”现象。图6（c）为基于图5中有键相硬件触发阶次跟踪方法的阶比谱，图中在轴承故障特征频率的1、2、3倍频处均存在清晰谱峰，故障特征明显。图6（d）为利用文中无键相阶次跟踪方法的阶比谱，与图6（c）具有较高一致性，平均误差小于5%，且由于进行了等角度同步平均处理，相比5（d）拥有更高的信噪比。

图5 有键相硬件触发阶次跟踪

图6 有键相硬件触发阶次跟踪

3 结论

针对车轮、轴承等旋转部件故障特征信号在车轮转频不断变化下非平稳的特点，以及我国部分车型无法提供车轮转速键相信号接口的实际情况，开展了无需转速键相信号的阶次跟踪方法研究。在进行转速估计时，根据列车网中周期发送的列车运行速度对旋转部件振动信号时频分布进行有约束的峰值提取以获取转速，并通过等角度重采样、角度域同步平均降噪等处理实现对无键相铁道车辆的旋转部件阶次跟踪。根据旋转部件故障试验台实测数据设计的验证试验表明，本方法计算的阶比谱与传统有键相硬件触发阶次跟踪的阶比谱平均误差小于5%，一致性较强，能够避免在无键相铁道车辆旋转部件在常规快速傅里叶分析中出现的“频率模糊”现象。