电磁差速耦合轮对导向机理*

李涛涛，刘建新

（西南交通大学 牵引动力国家重点实验室，成都 610031）

由于独立旋转车轮的两侧车轮是完全独立旋转的，其自动对中能力和曲线通过能力较差的导向问题催生了耦合轮对的提出。所谓耦合轮对，就是通过某种耦合方式将同一轮对上的两侧车轮间形成一定的耦合联系。

自从Benington［1］提出耦合轮对概念后，国内外许多学者也提出各自的耦合轮对技术方案。诸如：弹性阻尼耦合器式［2］、磁力可控耦合器式［3］、磁流体耦合器 式［4］、电轴耦合式［5］以及干摩擦副式［6］。以上各种耦合轮对技术方案提出后，其导向性能一直是领域内各位学者关注的焦点。王军平［7-8］分析了弹性—阻尼耦合轮对的耦合刚度和耦合阻尼对车辆系统的直线稳定性和曲线通过性能的影响，并确定了最佳耦合度的取值范围。Ma等人［9］在分析弹性阻尼耦合轮对纵向振动特性中，发现弹性阻尼耦合轮对的两侧车轮的耦合导致轮轴扭转振动，这一振动引起两侧轮纵向蠕滑力的不同，进而导致轮对纵向颤振现象。文献［10］分析了磁流体耦合轮对转向架前后轮对的耦合度对曲线通过性能的影响规律，并对同一转向架的前后轮对耦合度进行优化配置。根据摩擦限滑差速器的结构建立了横向摩擦耦合轮对的力学模型，Leng H等人［11］研究了摩擦耦合轮对的曲线性能和临界转速，并分析了摩擦力矩对动态性能的影响。文献［12］基于摩擦副耦合轮对的理论模型提出了一种根据轮对横向位移设计摩擦扭矩的方法，结果表明摩擦副耦合轮对具有传统刚性轮对相似的导向性能。以上研究表明耦合轮对具有比独立旋转车轮更好的导向性能，同时，以上各种耦合轮对形式均是通过某种耦合方式实现两侧车轮转速同步，从而使得轮轨处可以产生纵向蠕滑力。

除上述的几种同步转速的耦合轮对，还有学者提出了两侧车轮可以形成一定转速差的差速耦合轮对［13］。这种耦合轮对将应用在汽车上的机械差速器应用到耦合轮对上，以实现轮对的两侧车轮在必要时可以差速运行。继而文献［14］对比分析了分别装有机械差速器耦合轮对、传统轮对和独立旋转车轮的轨道车辆在曲线和直线上的导向性能，发现机械差速器耦合轮对也能较好地解决独立旋转车轮的导向问题。机械差速器作为左右车轮差速运行的被动控制装置，结合主动控制系统实现独立车轮横向机械差速控制，以使得左右轮对与轨道的接触均为纯滚动，不产生轮轨间轮缘的挤压与磨耗［15］。

文中根据机械差速器耦合轮对的差速轮对技术原理，提出了一种新型的采用电磁耦合器的耦合轮对—电磁差速耦合轮对。电磁差速耦合轮对是通过电磁耦合器将两侧独立旋转车轮通过轮系传动进行耦联，且两侧车轮转速差是可控的。

1 电磁差速耦合轮对的导向机理

电磁差速耦合轮对的结构如图1所示，其由左右侧车轮、轴桥、电磁耦合器和齿轮传动构成。

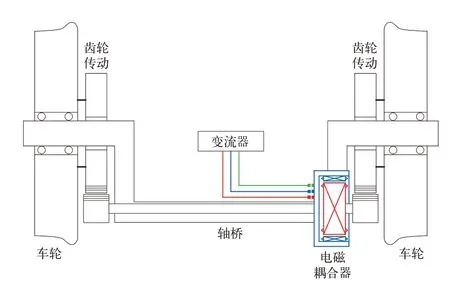
图1 电磁差速耦合轮对结构示意图

1.1 电磁耦合器原理

电磁差速耦合轮对为实现两侧车轮转动耦合且转速差可控，文中对电磁耦合器的结构进行了设计。电磁耦合器的结构如图2所示，即1台定子可以旋转的交流感应电机，旋转的定子称为外转子，转子称为内转子。内外转子通过齿轮传动分别与两侧车轮连接形成机械传动通路，实现将两侧车轮转动耦合；外转子上设三相绕组通过集电环和电刷与变流器形成电气通路，利用变流器控制输出电流以控制内外转子间转速差。

图2 电磁耦合器结构示意图

由于电磁耦合器是从笼式异步电机演化而来的，因此分析电磁耦合器的特性，最有效的方法就是等效电路法［16］。仿照异步电机的等效电路分析方法，根据归算前后保证电磁耦合器的通电端口的电磁性质不发生改变的归算原则，绕组的归算关系为式（1）［17］：

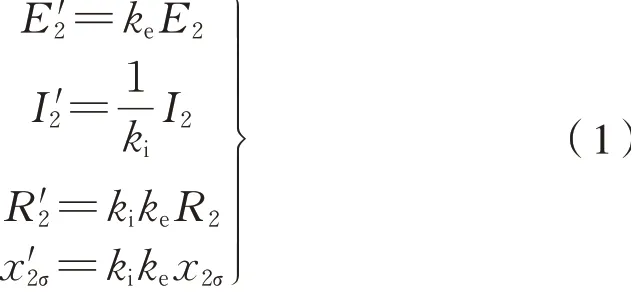
式中：E2，E′2为归算前后的内转子绕组电势；I2，I′2为归算前后的内转子绕组电流；R2，R′2为归算前后的内转子绕组电阻；x2σ，x′2σ为归算前后的内转子绕组漏电感；ke为电势归算系数，且为电流归算系数，且其中m1，m2为内外转子绕组相数，N1kw1，N2kw2为内外转子的有效匝数。根据以上归算后，则电磁耦合器的T型等效电路如图3所示［18］。

图3 电磁耦合器的T型等效电路[19]

在归算过程中，由于将内转子等效为相对于外转子的静止转子，故出现了如图3中所示的虚拟电阻从而有虚拟电阻的电功率即是电磁耦合器内外转子间通过气隙磁场传递的机械功率，该功率Pe为式（2）：

式中：s为电磁耦合器的转差率，其表达式为式（3）：

式中：ω为外转子绕组通电角频率；ωi为内转子转动角频率；ωo为外转子转动角频率。

根据式（2）分析电磁耦合器能量转化关系，若Pe为负值则表示虚拟电阻作为等效电路中的电源，吸收耦合轮对系统的机械能转化成电能。若Pe为正值则表示虚拟电阻在等效电路中为用电器，可以将电能转化为电磁差速耦合轮对系统的机械能。根据式（2）、式（3）可以得到电磁耦合器所传递的转矩Te为式（4）：

1.2 电磁耦合轮对导向机理分析

电磁耦合器内外转子间的电磁力矩是将轮对的两侧车轮旋转运动耦合起来的关键。文中利用电磁耦合器内外转子间的电磁力矩和电磁差速耦合轮对的纵向蠕滑力之间的关系，分析电磁差速耦合轮对在主动控制系统作用下的导向机理。为获得这两者间的关系，对电磁耦合轮对进行受力分析，如图4所示。图4中坐标系为右手坐标系，且x轴正方向为轮对前进方向。

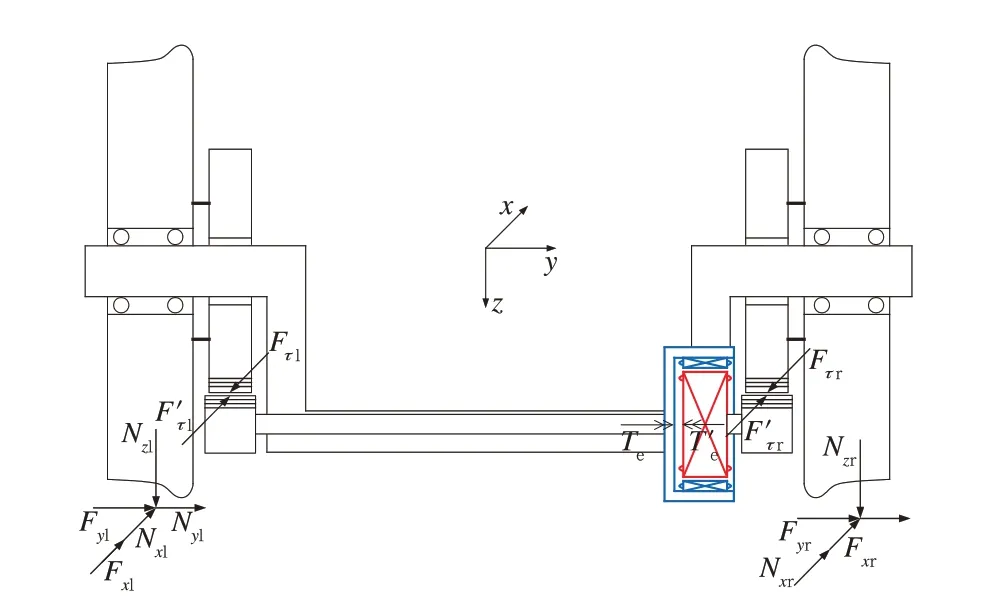
图4 电磁差速耦合轮对受力图

左侧车轮稳态的点头运动为式（5）：

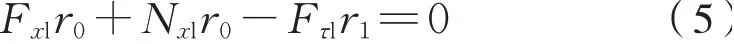
内转子稳态的旋转运动为式（6）：

右侧车轮稳态的点头运动为式（7）：

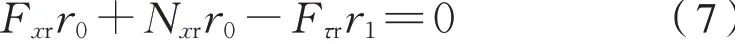
外转子稳态的旋转运动为式（8）：

式（5）~式（8）中：F xl，F xr分别为左右侧车轮纵向蠕滑力；N xl，N xr分别为左右侧轮轨法向力在纵向的分量；Te，T′e为电磁力矩，且Te=T′e；Fτl，F′τl，Fτr，F′τr为齿轮啮合圆周力，Fτl和F′τl互为反作用力，Fτr和F′τr互为反作用力；r0为名义滚动圆半径；r1，r2为齿轮节圆半径；i=r1/r2为齿轮传动比。

分别将式（6）代入式（5）、式（8）代入式（7）可得式（9）：

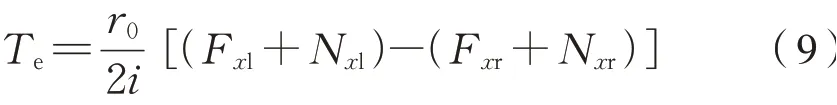
设纵向蠕滑力矩为M=(F xl-F xr)b，其中b为名义滚动圆横向跨距之半。且在轮对正常运行时，接触点不会偏移车轮踏面最低点很多，故左右侧轮轨法向力在纵向的分量可忽略不计，则有式（10）：

进一步将式（4）代入式（10）中可得式（11）：

根据式（2）和式（11）分析电磁差速耦合轮对在直线线路和曲线线路2种工况下不同运行状态的导向机理。

直线线路运行工况：

（1）当ωi>ωo时，即电磁差速耦合轮对的外侧车轮转速大于内侧车轮转速，轮对会形成正的摇头角从而偏离轨道中心向轨道内侧运动。若使得外转子绕组通电角频率ω近似为零，则轮对的纵向蠕滑力矩M的值为负值，轮对在负的纵向蠕滑力矩下形成负的摇头角向着轨道中心运动。另外，电磁耦合器的耦合功率Pe为正值，故电磁耦合器在消耗电磁差速耦合轮对的机械能，使得两侧车轮转速趋同。进一步验证了电磁耦合轮对拥有了像传统刚性轮对那样的直线对中能力。

（2）当ωi<ωo时，即电磁差速耦合轮对的外侧车轮转速小于内侧车轮转速，轮对会形成负的摇头角从而偏离轨道中心向轨道外侧运动。但轮对的纵向蠕滑力矩M的值为正值，轮对会形成正的摇头角恢复到线路中心运行。

曲线线路运行工况：

（1）当ω>ωi-ωo时，即外转子通电角频率控制期望ω未达到电磁耦合器内外转子间转速差控制期望。纵向蠕滑力矩M的值为正值，则轮对形成正的摇头角，从而使得轮对以趋向于轨道径向位置的姿态通过曲线。同时，电磁耦合器传递的机械功率Pe为正值，可见电磁耦合器将电能转化为驱动内外转子间形成转动差的机械能，继而使轮对顺利通过曲线。

（2）当ω<ωi-ωo时，即电磁耦合器内外转子间转速差大于控制期望。轮对的纵向蠕滑力矩M的值为负，则轮对摇头角在纵向蠕滑力矩的作用下不断减小直至回到轮对径向位置。且耦合器传递的电磁耦合功率Pe为负值，说明电磁耦合器作为电路中的电源，将形成内外转子转速差的机械能转化为电磁耦合器电路回路中的电能。

2 电磁耦合轮对仿真分析

文中研究电磁耦合轮对的导向能力，在Simpack多体动力学仿真分析软件中分别建立与电磁耦合轮对轨道车辆模型和除轮对形式外其他参数均相同的独立旋转轮对车辆模型。主要动力学参数见表1。

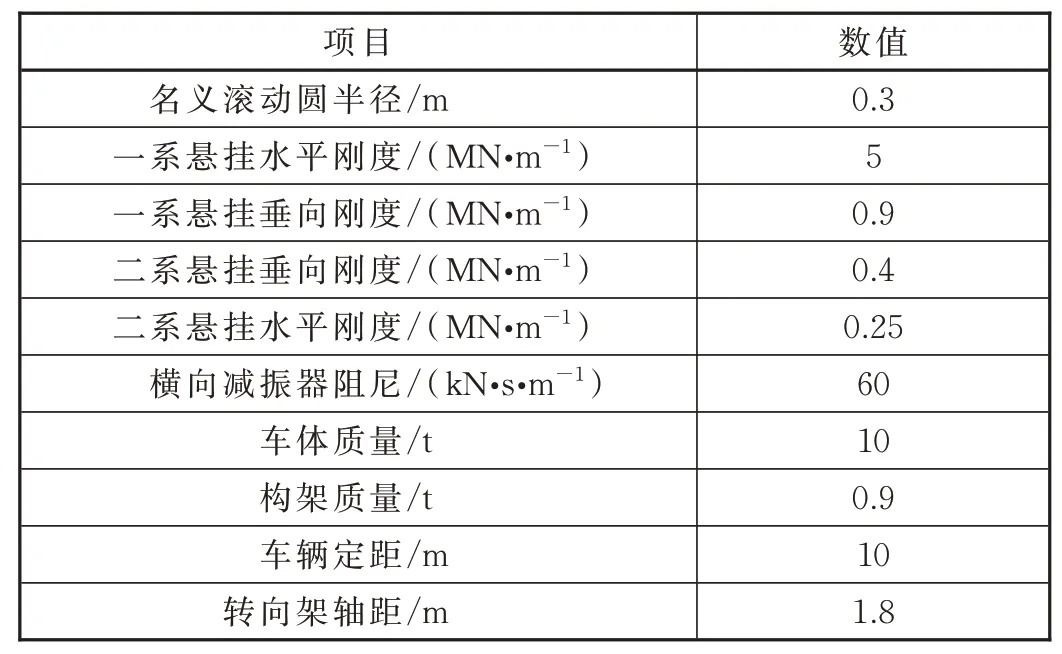
表1 主要动力学参数

2.1 直线对中能力

如果轮对偏离其线路的中心位置，其横移量若能够在较短的时间内收敛到0，则说明其具有较好的直线自动对中能力。设置车辆直线行驶速度为72 km/h，且初始横移量为4 mm［18］，对比独立旋转车轮、电磁耦合轮对的直线自动对中能力。

一位轮对横移量的仿真结果如图5所示，电磁差速耦合轮对的横移量在开始的0.2 s内快速接近0，经过一段时间后在0附近小幅振荡，轮对回到轨道中心，表明轮对具有很好的直线自动对中能力，而独立旋转车轮的轮对横移量缓慢的接近于0。这是因为电磁差速耦合轮对的两侧车轮的点头运动相互耦合。当两侧车轮转速不相等时，耦合器会产生耦合力矩，相应地轮轨接触处会产生纵向蠕滑力以平衡耦合器的耦合力矩。轮对从而在纵向蠕滑力矩的作用下趋向轨道中心运动，而独立旋转轮对理论上不存在纵向蠕滑力，因此趋近轨道中心的速度很慢。

图5 一位轮对横移量对比

2.2 曲线通过能力

衡量机车车辆曲线通过性能的几个重要指标是轮轨冲角、轮轨横向力和脱轨系数［20］。文中设定曲线半径为100 m，车辆运行速度为36 km/h［18］。选取一位轮对在通过曲线时的时域响应进行对比分析，如图6所示。

图6（a）为轮对的两侧车轮转速差，图6（b）为轮对在通过曲线时的轮对横移量。结合图6（a）和图6（b）可以看出独立旋转车轮在刚进入缓和曲线（一位轮对运行至14 m左右位置）时，其轮对横移量迅速达到10 mm，即此时发生了轮缘贴靠钢轨，外侧车轮的滚动圆半径增加显著而内侧车轮的滚动圆半径减小，故产生了较大的转速差波动。

另外，根据差速型轮对以曲线径向位置的姿态通过曲线时，外侧车轮前进速度为内侧车轮前进速度为可得在通过圆曲线时，左右车轮转速差期望值为式（12）：

式中：b为滚动圆横向跨距之半；v为轮对质心前进速度；R为圆曲线轨道中心线半径；r0为名义滚动圆半径。将仿真条件代入式（12）计算得到左右车轮转速差期望值为0.498 rad/s。图6（a）显示独立旋转车轮的两侧车轮转速差通过曲线线路过程中始终都未达到转速差期望值，外侧车轮则会滞后于内侧车轮。

图6（c）为一位轮对的轮轨冲角仿真结果，其表明电磁耦合轮对的轮轨冲角较于其他2种轮对小，可以认为电磁差速耦合轮对以趋近线路径向的姿态通过曲线。这是因为独立旋转车轮的外侧车轮在沿线路方向上的位置存在着一定程度滞后于内侧车轮，故形成了较大的轮轨冲角。

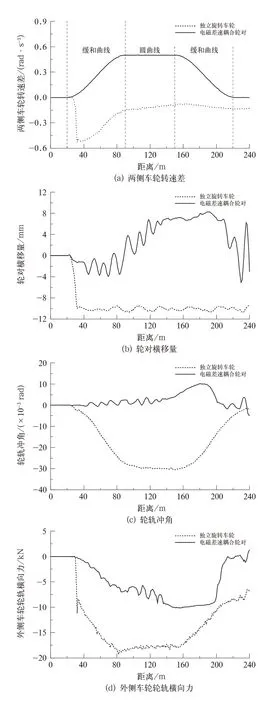
图6 通过曲线时一位轮对的时域响应

图6（d）和图6（e）分别为一位轮对外侧车轮的轮轨横向力和脱轨系数，其显示了电磁差速耦合轮对在圆曲线（90~150 m路段）上运行过程中，其外侧轮轨横向力相较于其他2种轮对低了44%，外侧车轮脱轨系数低了近39%。综上所述，电磁差速耦合轮对在通过小半径曲线时，具有很好的安全性能。

由于轮对在小半径曲线时，会出现轮缘区与钢轨接触，轮缘区域内的等效接触角较大，故自旋蠕滑的现象较为突出，在计算轮轨磨耗功率时增加考虑了自旋蠕滑。通过根据文献［21］给出的轮轨接触处的磨耗功率P为式（13）：

式中：Fx，Fy，T z分别为纵向蠕滑力、横向蠕滑力和自旋蠕滑力矩，ξx，ξy，ξs分别为纵向蠕滑率、横向蠕滑率和自旋蠕滑率，其轮轨的蠕滑率/力（矩）仿真结果结果如图7所示。

图7（a）、图7（b）、图7（c）分别为一位轮对外侧车轮的轮轨横向、纵向和自旋蠕滑率/力（矩）。由于电磁差速耦合轮对的轮轨冲角明显小于其他2种轮对形式的，致使电磁差速耦合轮对的横向蠕滑率也明显小于独立旋转车轮的横向蠕滑率。另外，电磁差速耦合轮对是可以主动差速，两侧车轮的转速在通过曲线时则可以形成一定的差值，这一差值可以弥补轮对两侧车轮在相同时间内需要走过距离的差值，因此其纵向蠕滑率也相对较小。图7（c）显示出独立旋转车轮的自旋蠕滑率明显大于电磁差速耦合轮对，这是因为独立旋转车轮在通过曲线时，轮缘始终贴靠钢轨运行，这使得自旋蠕滑率较大。

图7 一位轮对外侧车轮蠕滑率/力（矩）

根据式（13）计算独立旋转车轮和电磁差速耦合轮对的外侧车轮轮轨磨耗功率，结果如图8所示。由图8可见电磁差速耦合轮对的磨耗功率在通过曲线时明显低于独立旋转车轮。综上所述，电磁差速耦合轮对可以较好地解决独立旋转车轮曲线通过能力不足的问题。

图8 一位轮对外侧车轮磨耗功率

3 结论

研究的结论如下：

（1）针对独立旋转车轮存在导向性能不足的问题，文中提出了在独立旋转车轮基础上横向加装电磁耦合器的耦合轮对结构方案。

（2）电磁差速耦合轮对的导向机理：在直线线路运行时，若使得电磁耦合器内外转子间的转速趋于同步，电磁差速耦合轮对的纵向蠕滑力矩会抑制轮对形成摇头角，以使轮对趋近轨道中心运行。在曲线线路运行时，若电磁耦合器内外转子间的转速差小于期望值，电磁耦合器的耦合功率为正值，可以迫使轮对两侧车轮形成转速差，从而使轮对以趋近曲线线路径向位置的姿态通过曲线。若电磁耦合器内外转子间的转速差大于期望值，轮对摇头角在负的纵向蠕滑力矩作用下不断减小直至回到轮对径向位置。

（3）通过对独立旋转车轮和电磁差速耦合轮对的仿真结果对比分析发现：电磁差速耦合轮对的直线自动对中能力和曲线通过时安全性能和轮轨磨耗性能均优于独立旋转车轮，说明了电磁差速耦合轮对可以解决独立旋转车轮的直线自动对中能力和曲线通过能力不足等问题。

（4）结合工程实际，研究电磁耦合器本身的结构设计及空间布置，同时，关注运用环境下电磁耦合轮对的安全可靠性等问题。